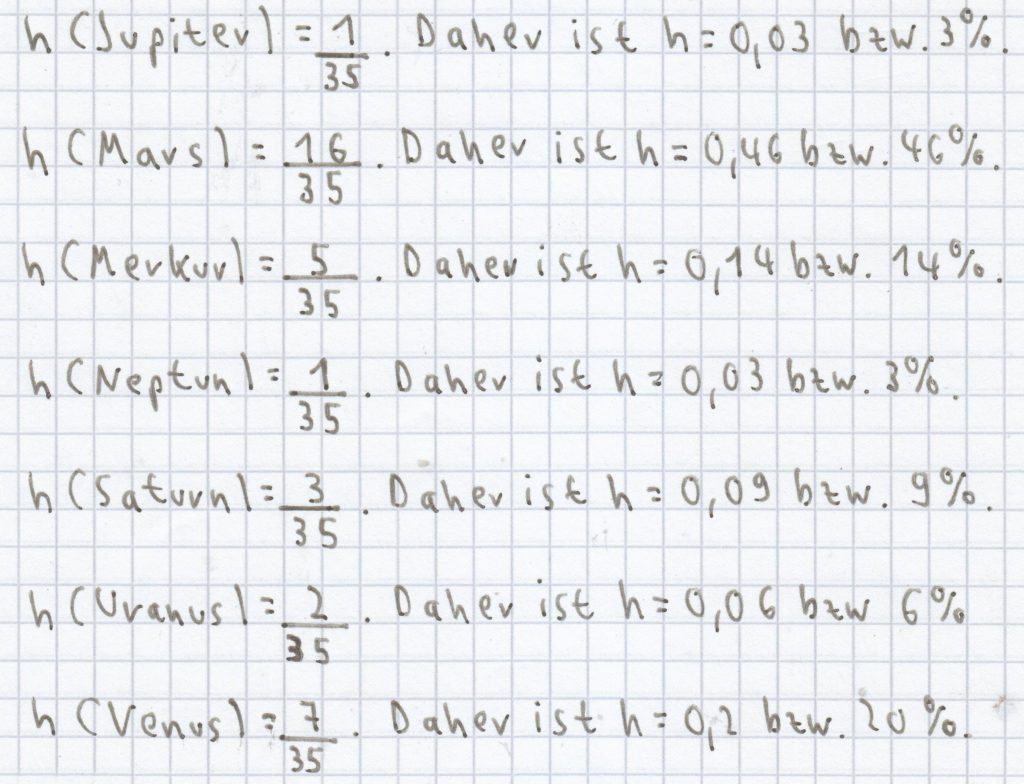Die bekannteste in Anführungszeichen Strichliste in der Literaturgeschichte stammt aus einem Märchen, das jeder kennt: „Das tapfere Schneiderlein“. In dem Grimm’schen Märchen trägt nämlich die Hauptfigur der Geschichte, ein armer Schneider, an seinem Gürtel die aufgestickten hochmissverständlichen Worte: „Sieben auf einen Streich.“ Unendlich stolz, weil er während des Essens von Pflaumenmus mit einem einzigen Tuchlappen-Schlag sieben lästige Fliegen ins Jenseits beförderte, verewigt das Schneiderlein diese „Heldentat“ auf seinem Gürtel. Doch jene Strichliste in Worten wird jedoch prompt natürlich dahingehend falsch verstanden, dass das Schneiderlein 7 Männer „auf einen Streich“ getötet habe. Dadurch beginnt das große Abenteuer des vermeintlich tapferen Schneiderleins, das – wie kann es in einem Grimm’schen Märchen anders sein – für den ungewollten Superhero schließlich trotzdem ausgesprochen gut zu Ende geht.

Sieben Kerben im Gürtel, die gleich einer Strichliste dort verewigt worden wären, hätten übrigens sicherlich auch schon genügt, damit das Schneiderlein ebenso fälschlicherweise zum Superhelden erklärt worden wäre.
Aufgaben zum Mathematik-Stoffgebiet: Statistik
1. Mathe-Nachhilfe-Aufgabe: Ermittelte bei der unten auf dem Bild aufgezeichneten Strichliste zur Weite eines Kaugummiweitspuckwettbewerbs jeweils die Grundgesamtheit (n), die absolute Häufigkeit (H) und die relative Häufigkeit (h).
2. Mathematik-Nachhilfe-Aufgabe: Berechne ebenso auf der unten auf dem Bild dargestellten Strichliste zu Lieblingsfabeltieren der tierischen Fabeltiere stets die Grundgesamtheit (n), die absolute Häufigkeit (H) und die relative Häufigkeit (h).
3. Mathematik-Nachhilfe-Aufgabe: Bestimme ebenfalls auf der unten auf dem Bild zu sehenden Strichliste zu Planeten, wohin nach Meinung einer Schulklasse Menschen im 25. Jahrhundert Planetenraumfahrten gemacht haben, die Grundgesamtheit (n), die absolute Häufigkeit (H) und die relative Häufigkeit (h). Verschiedene Strichlisten

Lösungen zu dem Mathe-Stoffgebiet: Statistik
1. Lösungen zu der Mathematik-Nachhilfe-Aufgabe: Berechnung bestimmter statistischer Grundbegriffe anhand der Strichliste zur Weite eines Kaugummiweitspuckwettbewerbs
Die Grundgesamtheit n bei der Strichliste Kaugummiweitspuckwettbewerb ergibt sich aus der gesamten Anzahl aller Striche, die unter dem Merkmal Weite erfasst wurden. Da 13 Weiten erfasst wurden, ist die Grundgesamtheit n = 13.
Die absolute Häufigkeit H gibt wieder, wie oft eine bestimmte Weite bei der Grundgesamtheit aller Weiten vorkam. Von 13 an dem Kaugummiweitspuckwettbewerb teilgenommenen Personen spukten 3 den Kaugummi genau 2,53 m, 2 genau 2,45 m, 1 genau 3,47 m, 1 genau 3,05 m, 1 genau 2,74 m, 1 genau 2,47 m, 1 genau 2,31 m, 1 genau 1,51 m, 1 genau 1,03 m und 1 genau 0,65 m.
H (die absolute Häufigkeit) für die Weite 3,47 m = 1, für die Weite 3,05 m ist H = 1, für die Weite 2,74 m ist H = 1, für die Weite 2,53 m ist H = 3, für die Weite 2,47 m ist H = 1, für die Weite 2,45 m ist H = 2, für die Weite 2,31 m ist H = 1, für die Weite 1,51 m ist H = 1, für die Weite 1,03 m ist H = 1, für die Weite 0,65 m ist H = 1.
Die relative Häufigkeit h aller bei dem Kaugummiweitspuckwettbewerb gespukten 13 Weiten ergibt sich jeweils aus dem Quotienten von absoluter Häufigkeit und Grundgesamtheit.
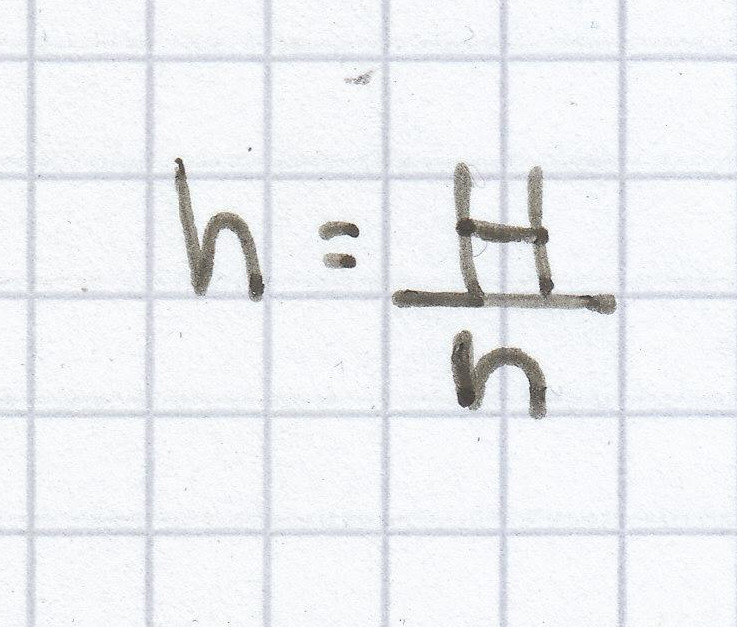
Alle Ergebnisse für h sind auf zwei Nachkommastellen hin gerundet!

2. Lösungen zu der Mathe-Nachhilfe-Aufgabe: Ermittlung bestimmter statistischer Grundbegriffe mittels der Strichliste zu Lieblingsfabeltieren der tierischen Fabeltiere.
Die Grundgesamtheit n bei der Strichliste tierische Fabeltiere setzt sich aus der Summe aller Striche zusammen, die unter dem Merkmal Lieblingsfabeltiere vermerkt wurden. Da 46 Lieblingsfabeltiere vermerkt wurden, ist die Grundgesamtheit n = 46.

Die absolute Häufigkeit H zeigt auf, wie oft ein bestimmtes Lieblingsfabeltier innerhalb der Grundgesamtheit Lieblingsfabeltiere genannt wurde. Von den 46 Personen, die ihr Lieblingsfabeltier nannten, waren genau 3 „Likes“ für die Chimäre, 11 „Likes“ für den Drachen, 10 „Likes“ für das Einhorn, 1 „Like“ für den Greif, 2 „Likes“ für die Hydra, 7 „Likes“ für den Pegasus, 2 „Likes“ für den Phönix, 6 „Likes“ für den Satyr und 4 „Likes“ für die Sphinx.
H (die absolute Häufigkeit) bei der Chimäre = 3, bei dem Drachen ist H = 11, bei dem Einhorn ist H = 10, bei dem Greif ist H = 1, bei der Hydra ist H = 2, bei dem Pegasus ist H = 7, bei dem Phönix ist H = 2, bei dem Satyr ist H = 6 und bei der Sphinx ist H = 4.
Die relative Häufigkeit aller genannten Lieblingsfabeltiere ergibt sich wiederum aus dem Quotienten von absoluter Häufigkeit und Grundgesamtheit.
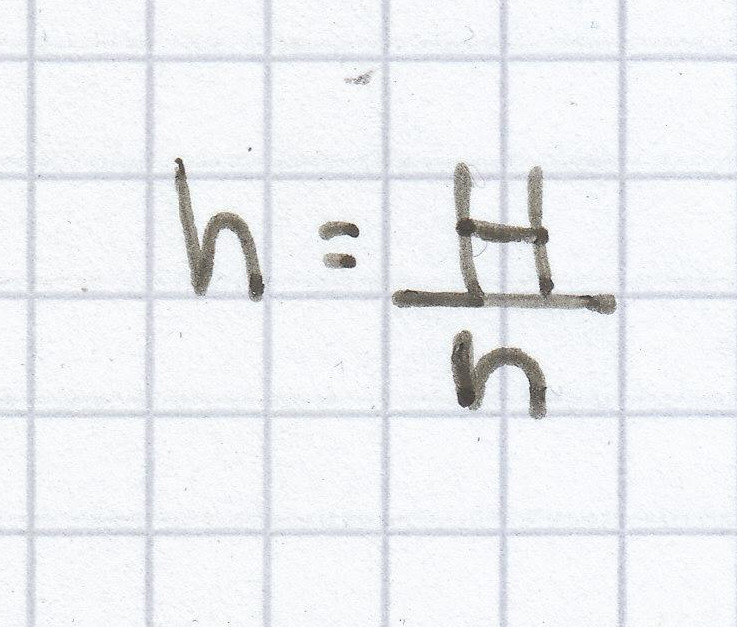
Alle Ergebnisse für h sind auf zwei Nachkommastellen hin gerundet!

3. Lösungen zu der Mathe-Nachhilfe-Aufgabe: Berechnung bestimmter statistischer Grundbegriffe mittels der Strichliste zu Planeten, zu denen nach Meinung einer Schulklasse Menschen im 25. Jahrhundert Planetenraumfahrten gemacht haben.
Die Grundgesamtheit n bei der Strichliste Planetenflüge im 25. Jahrhundert ergibt sich aus der Gesamtzahl aller Striche, die unter dem Merkmal Planeten erfasst wurden. Da 35 Planeten vermerkt wurden, ist die Grundgesamtheit n = 35.
Die absolute Häufigkeit zeigt an, wie oft ein bestimmter Planet bei der Grundgesamtheit Planeten bereist wurde. Von 35 im 25. Jahrhundert bereisten Planeten wurde der Jupiter 1-mal, der Mars 16-mal, der Merkur 5-mal, der Neptun 1-mal, der Saturn 3-mal, der Uranus 2-mal, und die Venus 7-mal bereist.
H (die absolute Häufigkeit) für den Jupiter = 1, für den Mars ist H = 16, für den Merkur ist H = 5, für den Neptun ist H = 1, für den Saturn ist H = 3, für den Uranus ist H = 2 und für die Venus ist H = 7.
Die relative Häufigkeit der bereisten Planten ergibt sich aus dem Quotienten von absoluter Häufigkeit und Grundgesamtheit.
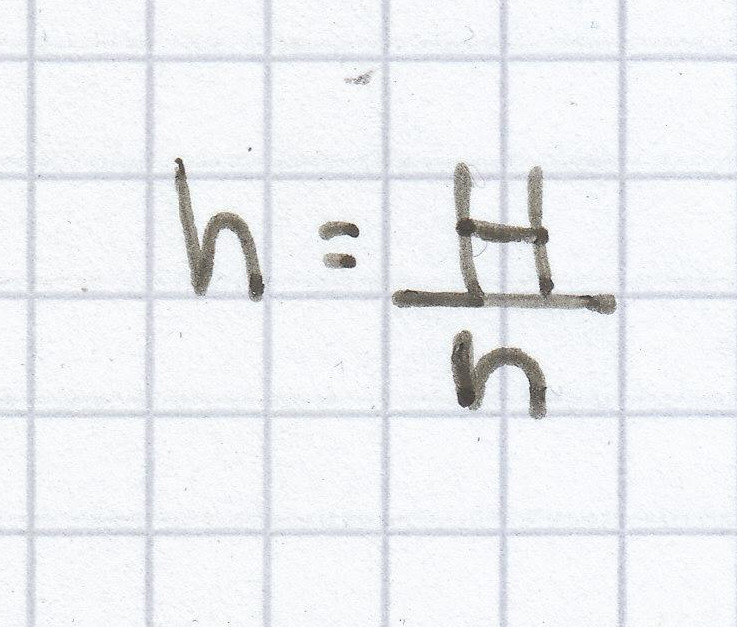
Alle Ergebnisse für h sind auf zwei Nachkommastellen hin gerundet!