
Ich bin nur Durchschnitt“ ist in unserer leistungsorientierten Gesellschaft eine negative Äußerung. Aber warum? Offenbar verhält es sich so, dass man mit einer durchschnittlichen Leistung etwas nicht wirklicht „gut“ macht beziehungsweise „gut“ kann. Aber ist demzufolge ein Durchschnittlichsein gleichzusetzen mit Mittelmäßigkeit? Die Antwort hierzu ist ein klares Nein. Denn Durchschnittlichkeit ist nicht an sich etwas Schlechtes. Wie eigentlich immer im Leben kommt es auch bei der Aussage „Ich bin nur Durchschnitt“ nämlich darauf an, auf was genau sie sich bezieht, das heißt auf die „Qualität“ des Durchschnittswertes. Je besser nämlich alle bei etwas Bestimmten sind, desto höher und „qualitativer“ ist das Durchschnittsergebnis – und umgekehrt. Daher lässt man am besten die Mathematik darüber entscheiden, ob man selbst wirklich Durchschnitt ist oder nicht. Da schließlich der Durchschnitt in Mathe immer ganz genau bestimmt werden kann, kann man hier auch stets augenscheinlich sehen, ob bei einer angeblichen Mittelmäßigkeit auch wirklich eine Mittelmäßigkeit vorliegt.
Aufgaben zum Mathematik-Stoffgebiet: Statistik

1. Mathematik-Nachhilfe-Aufgabe: Ermittle bei folgenden Zahlen den Mittelwert/das arithmetische Mittel und den Zentralwert/Median.
a) 76, 19, 35, 38, 85, 43 54, 73, 22, 37, 63
b) 39, 87, 18, 25, 47, 55, 71, 44, 79, 59
2. a) Mathe-Nachhilfe-Aufgabe: Bestimme bei folgenden Größen-Angaben jeweils den Mittelwert/das arithmetische Mittel und den Zentralwert/Median.
(1) 5,5 m, 5,4 m, 4,9 m, 5,0 m, 4,7 m, 4,8 m, 5,3 m, 5,4 m, 4,7 m, 5,3 m, 4,9 m
(2) 15,3 kg, 15,7 kg, 14,6 kg, 13,3 kg, 16,1 kg, 12,9, kg, 14,8 kg, 15,5 kg, 14,6 kg
(3) 35 s, 47 s, 39 s, 34 s, 40 s, 45 s, 55 s, 56 s, 45 s, 47 s, 55 s, 39 s
(4) 4,3 ha, 2,9 ha, 4,2 ha, 3,0 ha, 3,5 ha, 3,9 ha, 3,8 ha, 3,1 ha, 3,7 ha, 4,3 ha
(5) 5,2 cm³, 4,9 cm³, 5,2 cm³, 3,8 cm³, 3,5 cm³, 3,8 cm³, 4,8 cm³
2. b) Mathematik-Nachhilfe-Aufgabe: Überprüfe, wie sich der Mittelwert/das arithmetische Mittel und der Zentralwert/Median jeweils ändern, wenn man bei jeder Größen-Reihe stets den kleinsten und den größten Wert entfernt.
3. Mathe-Nachhilfe-Aufgabe: In einer Mathematik-Arbeit wurden folgende Noten geschrieben: 12 Schüler hatten eine 1 und 21 Schüler eine 2. Andere Noten gab es nicht. Ermittle bei den geschriebenen Mathe-Noten den Mittelwert/das arithmetische Mittel und den Zentralwert/Median.
Lösungen zu dem Mathematik-Stoffgebiet: Statistik
1. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Berechnung des Mittelwertes/arithmetischen Mittels und Zentralwertes/Medians bei vorgegeben Zahlen.
a) Der Mittelwert/das arithmetische Mittel (M) setzt sich aus der Summe aller Werte ( Wert 1 + Wert 2 + Wert 3 + … + Wert 11) geteilt durch die Grundgesamtheit (n) zusammen. Daraus ergibt sich:
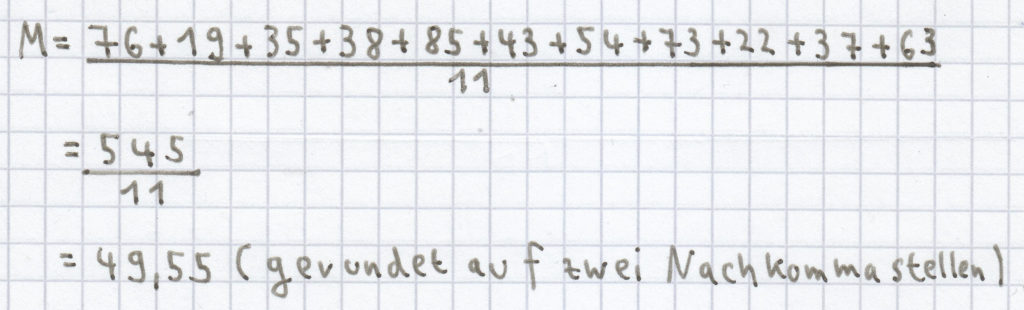
Der Zentralwert/Median (Z) ist bei einer geordneten, ungeraden Reihe an Werten, die beim kleinsten Wert beginnt und beim größten Wert endet, genau der in der Mitte liegende Wert. Daher ist der Zentralwert/Median bei folgender geordneten Reihe: 19, 22, 35, 37, 38, 43, 54, 63, 73, 76, 85 der an der 6. Position stehende Wert, da jeweils noch 5 Werte links und rechts davon stehen, und demzufolge ist Z = 43.
b) Der Mittelwert/das arithmetische Mittel (M) ergibt sich wie in Aufgabe a aus der Summe aller ermittelnden Werte (Wert 1 + Wert 2 + Wert 3 + … + Wert 10) geteilt durch die Grundgesamtheit (n). Daraus ergibt sich:
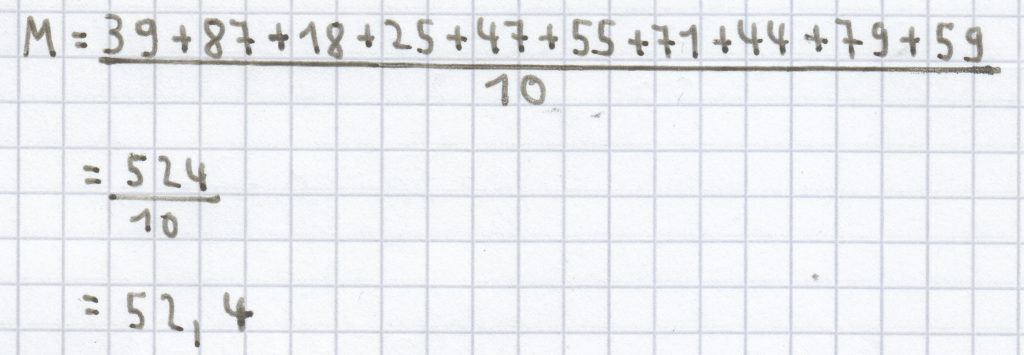
Der Zentralwert/Median (Z) ergibt sich aus einer geordneten, geraden Reihe, die mit dem kleinsten Wert beginnt und mit dem größten Wert endet, aus dem Mittelwert/arithmetischen Mittel beider in der Mitte stehender Werte. Daher ergibt sich bei folgender geordneten Reihe: 18, 25, 39, 44, 47, 55, 59, 71, 79, 87 als Zentralwert/Median der Mittelwert/das arithmetische Mittel aus dem 5. und dem 6. Wert, da jeweils noch 4 Werte links des 5. stehen und jeweils 4 nach dem 6. Demzufolge berechnet man Z folgendermaßen:
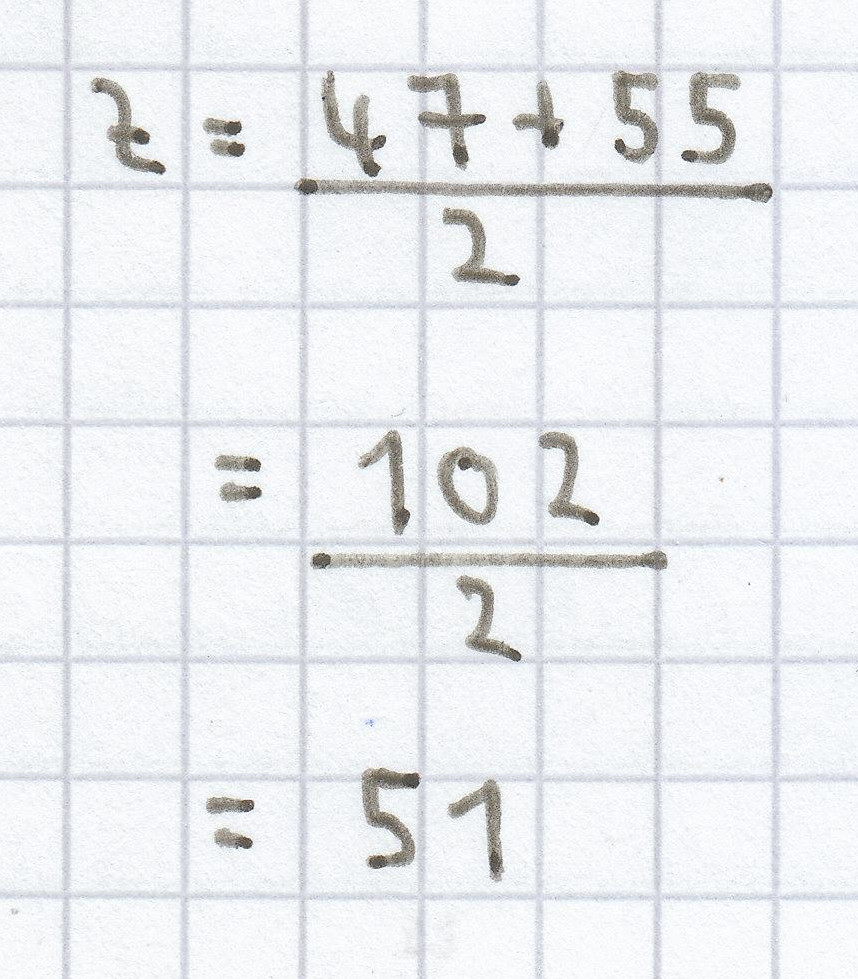
2. a) Lösung zu der Mathe-Nachhilfe-Aufgabe: Ermittlung des Mittelwertes/arithmetischen Mittels und des Zentralwertes/Medians bei Größen-Angaben.
(1) Der Mittelwert/das arithmetische Mittel (M) setzt sich aus der Summe aller erfassten Werte (Wert 1 + Wert 2 + Wert 3 + … + Wert 11) zusammen, geteilt durch die Grundgesamtheit (n). Daraus ergibt sich:
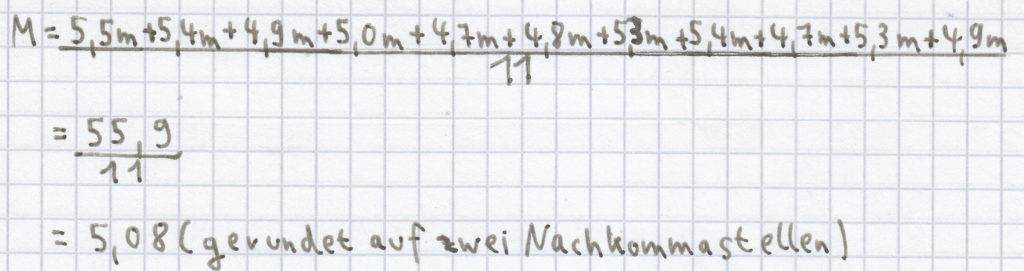
Der Zentralwert/Median ist bei einer geordneten, ungeraden Wertereihe, die vom kleinsten beginnt und bis zum größten hin geht, der in der Mitte stehende Wert. Daher ergibt sich aus folgender geordneten Reihe: 4,7 m, 4,7 m, 4,8 m, 4,9 m, 4,9 m, 5,0 m, 5,3 m, 5,3 m, 5,4 m, 5,4 m, 5,5 m als Zentralwert/Median: Z = 5,0 m, da jeweils 5 Werte noch links und 5 Werte noch rechts stehen.
(2) Der Mittelwert/das arithmetische Mittel (M) ergibt sich hier wie folgt:
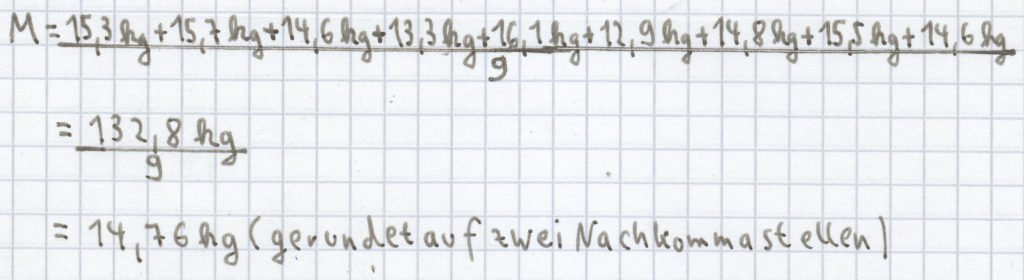
Der Zentralwert/Median aus folgender geordneten Reihe: 12,9 kg, 13,3 kg, 14,6 kg, 14,6 kg, 14,8 kg, 15,3 kg, 15,5 kg, 15,7 kg, 16,1 kg ist Z = 14,8 kg.
(3) Der Mittelwert/das arithmetische Mittel (M) setzt sich wie folgt zusammen:
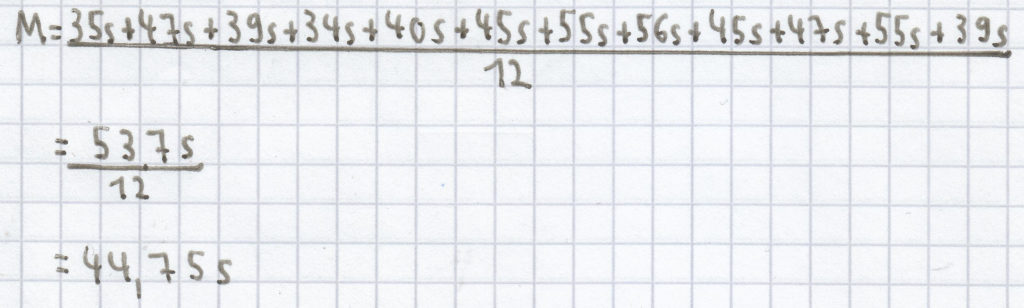
Der Median/Zentralwert (Z) ergibt sich hier aus dem Mittelwert/arithmetischen Mittel beider in der Mitte stehender Werte folgender geordneten Reihe: 34 s, 35 s, 39 s, 39 s, 40 s, 45 s, 45 s, 47 s, 47 s, 55 s, 55 s, 56 s. Daher ergibt sich für Z:
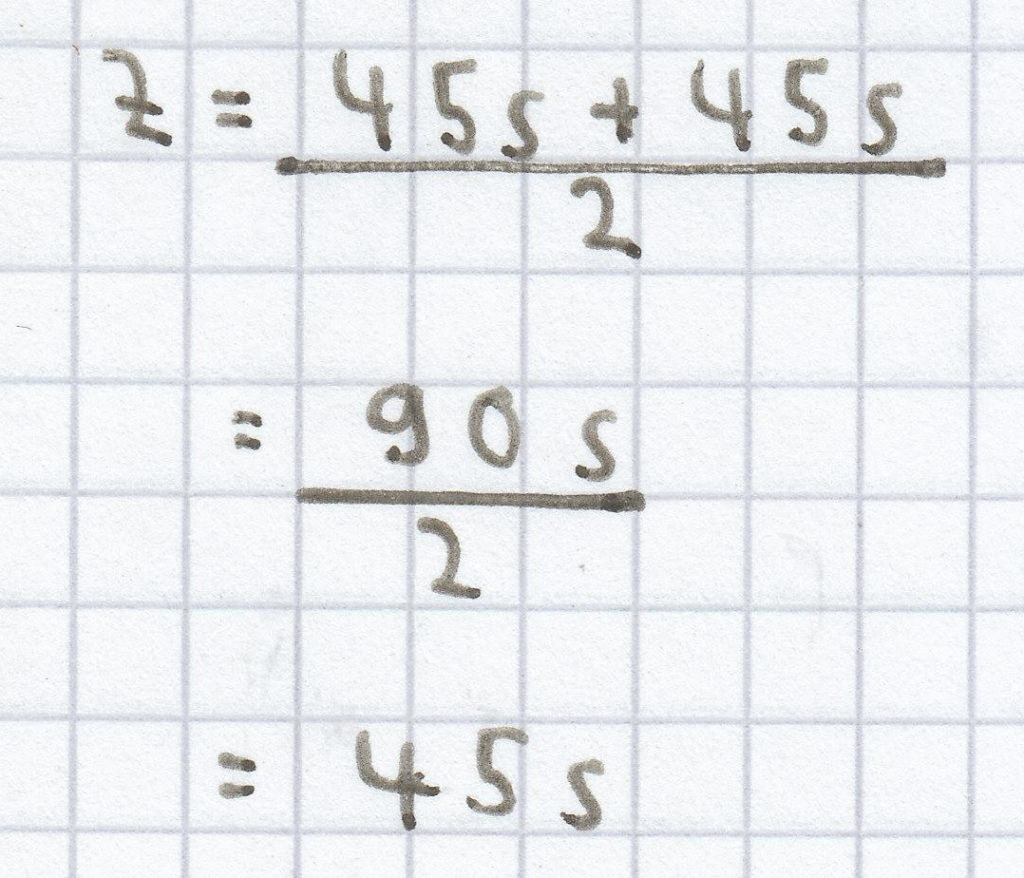
(4) Der Mittelwert/das arithmetische Mittel ist hier Folgendes:
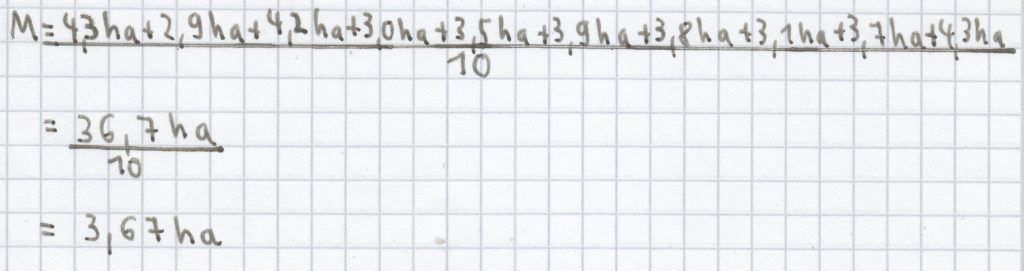
Der Zentralwert/Median ist aus dieser geordneten Reihe: 2,9 ha, 3,0 ha, 3,1 ha, 3,5 ha, 3,7 ha, 3,8 ha, 3,9 ha, 4,2 ha, 4,3 ha, 4,3 ha der Mittelwert/das arithmetische Mittel aus dem 5. und 6. Wert. Z berechnet sich daher folgendermaßen:
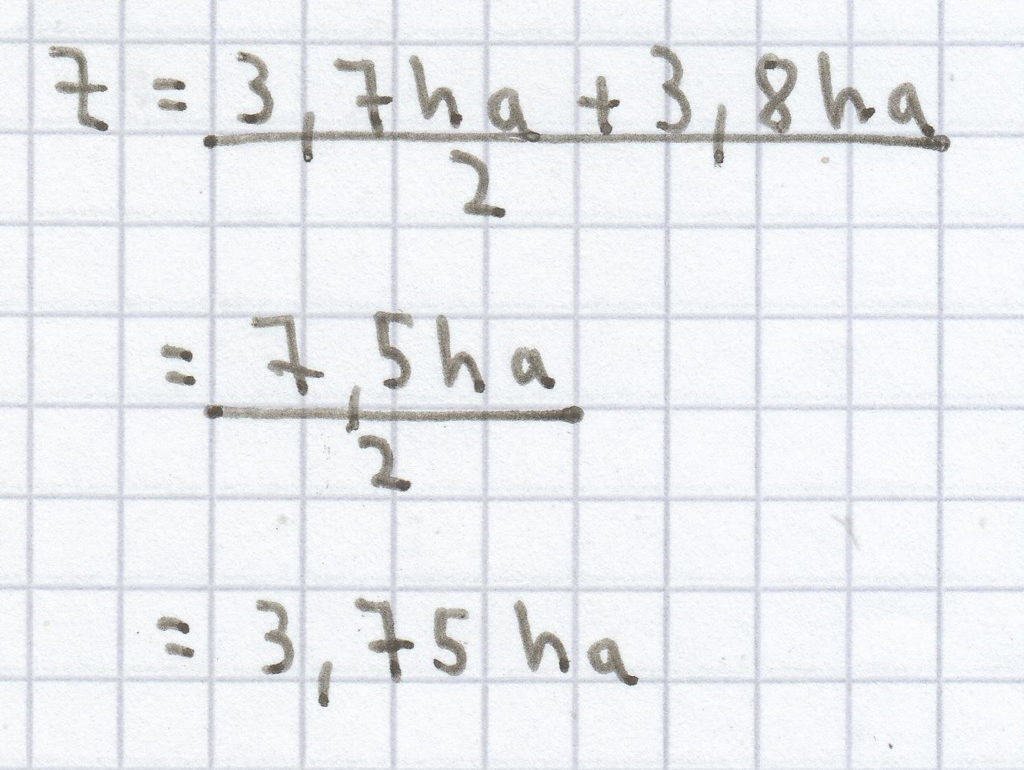
(5) Der Mittelwert/das arithmetische Mittel ergibt sich hier wie folgt:
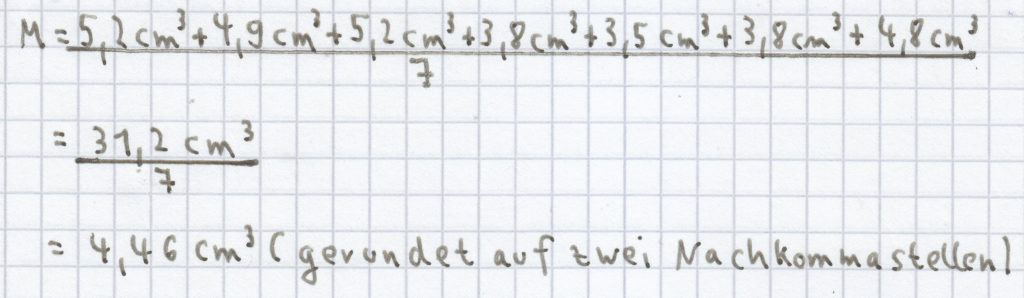
Der Zentralwert/Median aus dieser geordneten Reihe: 3,5 cm³, 3,8 cm³, 3,8 cm³, 4,8 cm³, 4,9 cm³, 5,2 cm³, 5,2 cm³ ist Z = 4,8 cm³.

2. b) Lösung zu der Mathe-Aufgabe: Überprüfe, wie durch das Wegfallen des kleinsten und des größten Wertes der Mittelwert/das arithmetische Mittel und der Zentralwert/Median sich ändern.
(1) Der Mittelwert/das arithmetische Mittel ergibt sich dann wie folgt:
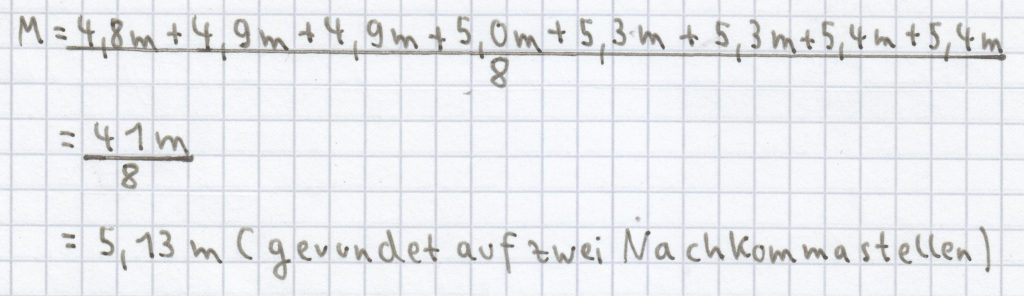
Der Zentralwert/Median ist dann folgender:
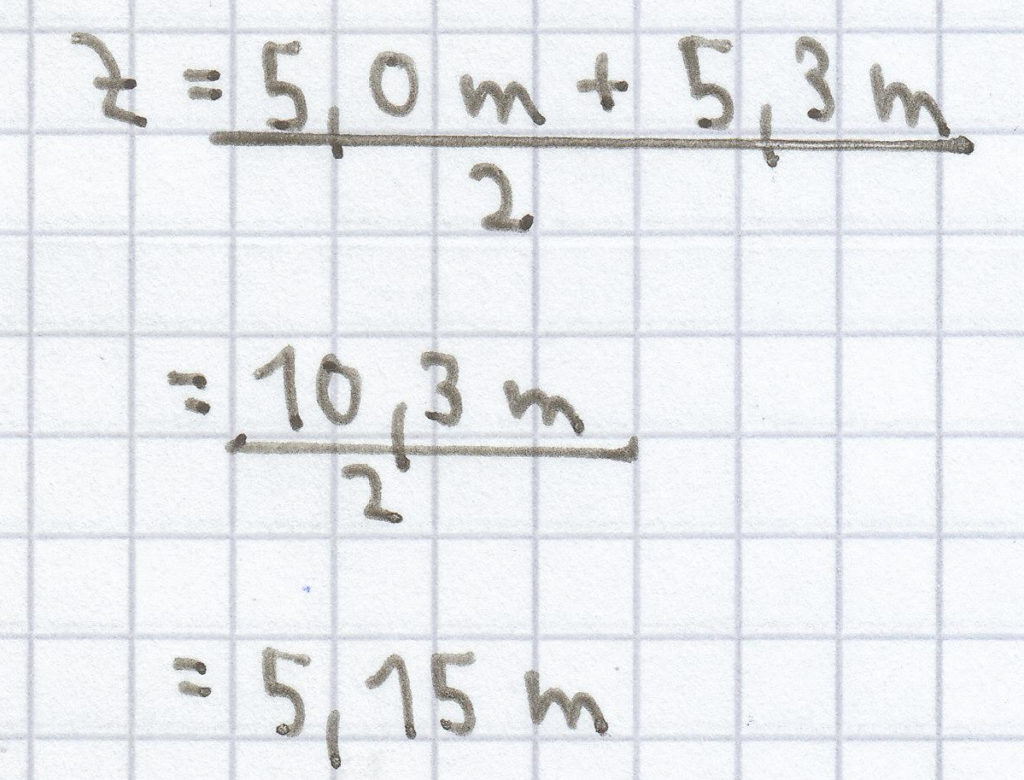
(2) Der Mittelwert/das arithmetische Mittel setzt sich nun folgendermaßen zusammen:
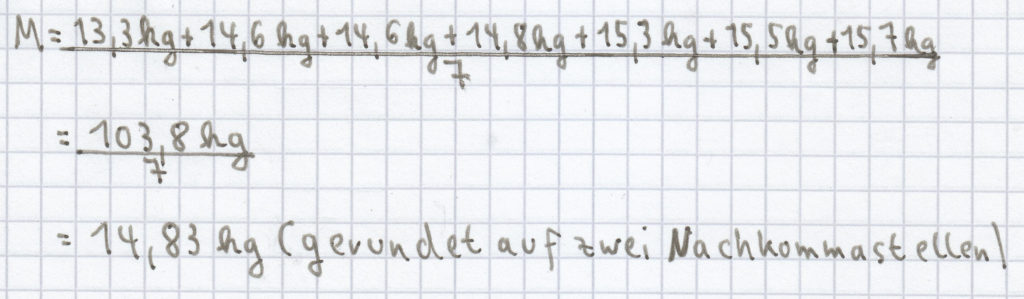
Der Zentralwert/Median ist dann dieser: Z = 14,8 kg.
(3) Der Mittelwert/das arithmetische Mittel berechnet sich nun folgendermaßen:
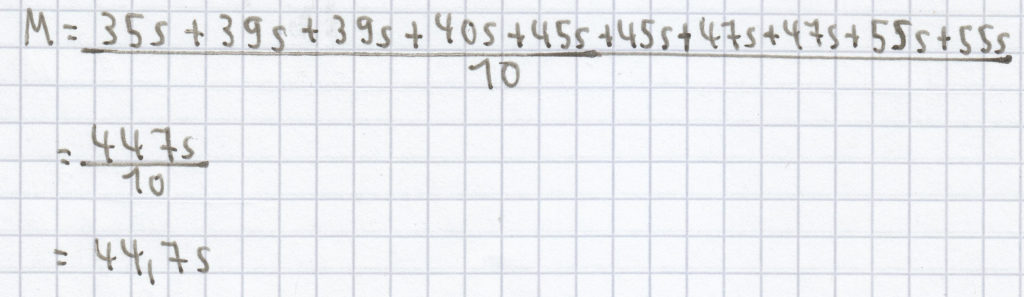
Folgender Zentralwert/Median ergibt sich nun:
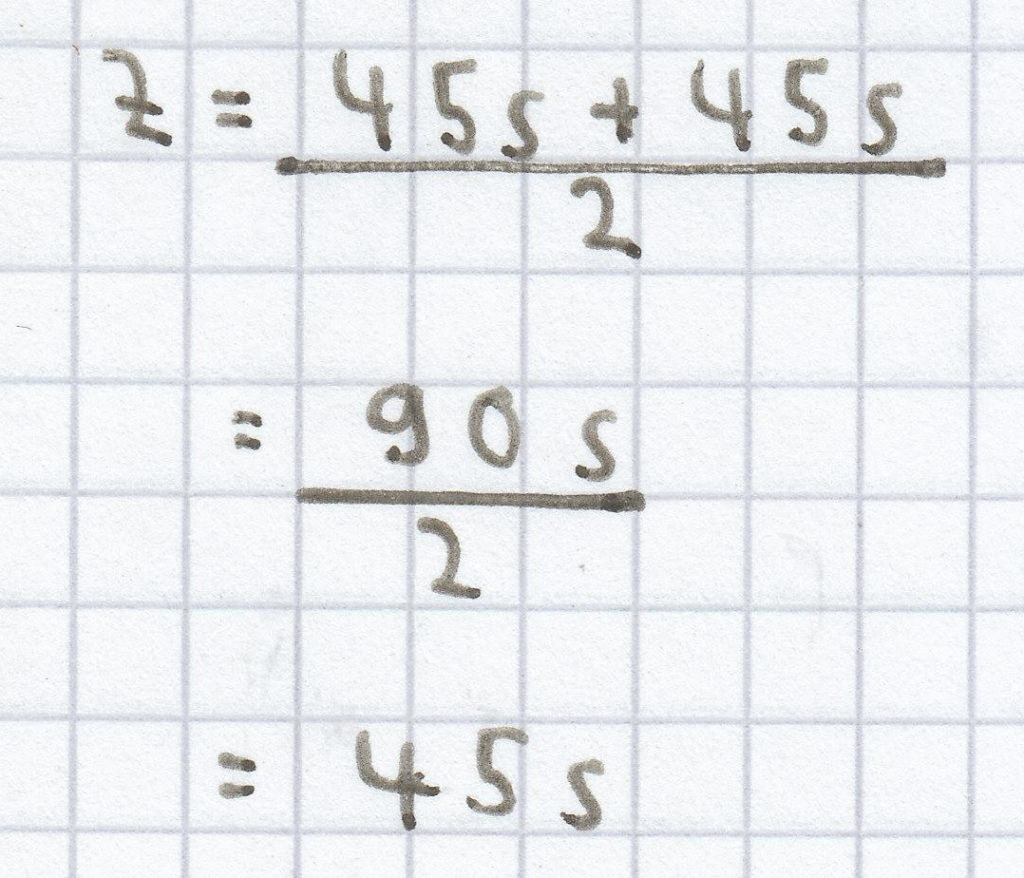
(4) Der Mittelwert/das arithmetische Mittel setzt sich nun wie folgt zusammen:
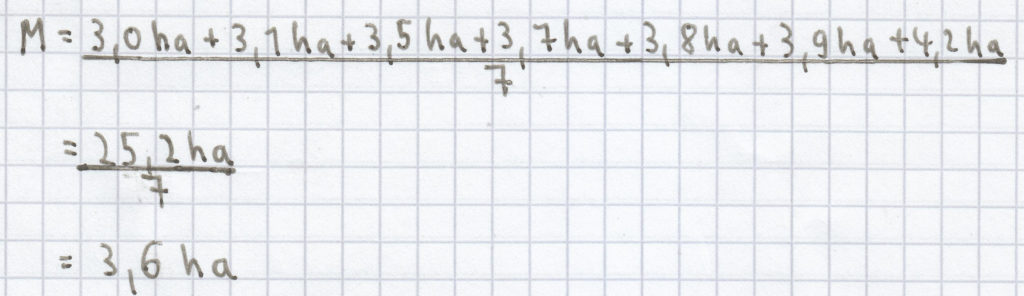
Der Zentralwert/Median ist nun dieser: Z = 3,7 ha.
(5) Der Mittelwert/das arithmetische Mittel ist nun hier Folgendes:

Der Zentralwert/Median ist nun hier Folgender:
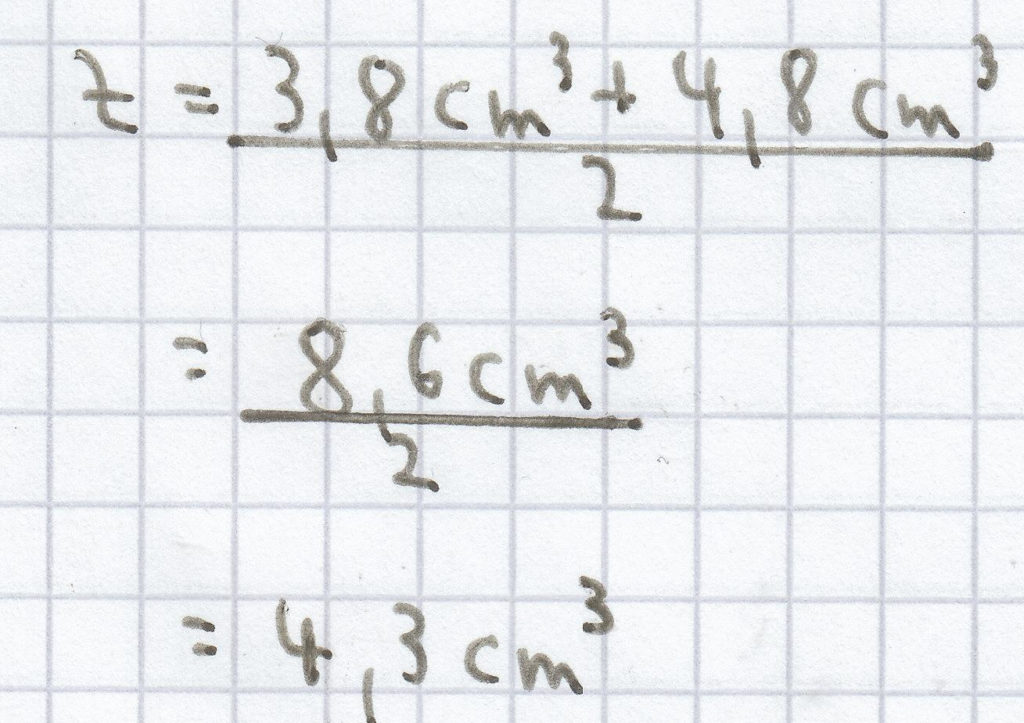
3. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Bestimme den Mittelwert/das arithmetische Mittel und den Zentralwert/Median des ermittelnden Mathematik-Klassenarbeitsergebnisses.
Der Mittelwert/das arithmetische Mittel ergibt sich hier folgendermaßen (als Zwischenrechnung wurde bereits ausgerechnet: 12 · 1 = 12 und 21 · 2 = 42):
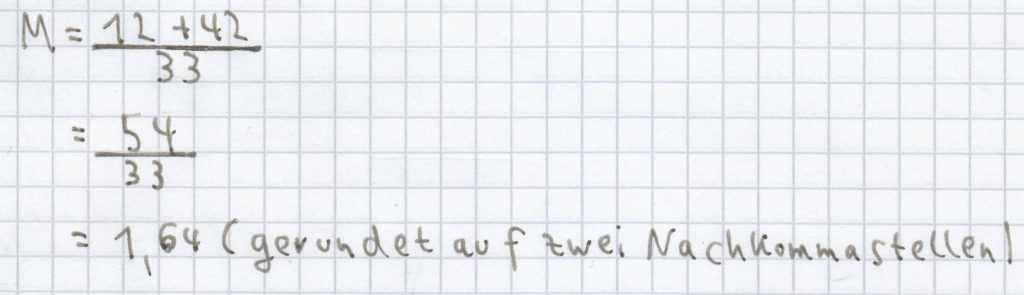
Als Zentralwert/Median ergibt sich hier aus folgender geordneten Reihe: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2
Z = 2.