
Überall, wo im Fach Mathe eine Unbekannte beziehungsweise in der Sprache der Mathematik gesprochen eine Variable vorkommt, findet man einen Term vor. Dieses ist nämlich sein Haupterkennungsmerkmal. Das Schwierige hierbei ist aber nicht, einen Term zu erkennen, sondern sein entscheidendes Charakteristikum auch richtig zu verstehen. Denn was bedeutet denn eine auftretende Variable in einem Term? Einen klaren Aufschluss hierzu gibt die Ursprungsbedeutung des Wortes „Variable“. Ein Variabel-Sein heißt nämlich nichts anderes als ein Nicht-genau-Festgelegtsein. Daher kann in die Variable eines Terms immer jede x-beliebige Zahl eingesetzt werden. Schließlich bezieht sich das Variabel- beziehungsweise Nicht-genau-Festgelegtsein auf eine konkrete Zahl.
Sehr gut lässt sich das Haupterkennungsmerkmal eines Terms auch an einer Gummibärchen-Packung erklären. Hierbei stellt der Inhalt der Packung die Variable x dar, da wir nicht genau wissen, wie viele Gummibärchen sich darin befinden. „X“ ist in diesem Beispiel auch zugleich der Term, da nichts weiter bei der Termaufstellung miteinfließt. In die Variable x können wir nun jede x-beliebige Zahl einsetzen. Schließlich ist die genaue Gummibärchen-Anzahl ja unbekannt. So könnte die Zahl 1 genauso wie die Zahl 5000000 eingesetzt werden – auch wenn beide Zahlen aufgrund der Packungsgröße und dem normalen Gewicht von 200 g absolute Gaga-Zahlen sind. Trotz allem kann und darf man eine x-beliebige Zahl in den Gummibärchenpackungs-Term x einsetzen – wenn keine Zahlenmenge explizit ausgeschlossen wurde. Sinn machen bei einer normalgewichtigen Gummibärchentüte aber verständlicherweise nur ganze Zahlen, da Gummibärchentorsos darin nicht enthalten sind. Als erfahrener Gummibärchenesser sagt mir außerdem mein Gefühl, dass mehr als 100 nicht drin sein dürften. Denn – Hand aufs Herz – spätestens beim Erbsen- bzw. Gummibärchenzählen hat der Spaß an der Mathematik auch bei mir ein Ende.
Aufgaben zum Mathe-Stoffgebiet Term
1. Mathematik-Nachhilfe-Aufgabe: Ermittle den jeweiligen Wert folgender Terme. Setze hierfür für x die Zahlen 0, 1, 5, 10, 18 und 52 ein.
a) 4x + 3
b) 7 · x – 2
c) 5 + (100 – 2x) · 5
d) (8 x + 4) : 2
e) (2x – 7)²
2. Mathe-Nachhilfe-Aufgabe: Gebe zu jedem nachfolgenden Term die Rechenvorschrift in einfachen Worten wie in den angegebenen Beispielen wieder (4x + 8: in Worten: Addiere 8 zum Vierfachen einer Zahl, (x + 7)² = (x + 7) · (x +7), in Worten: Addiere zu einer Zahl 7 und multipliziere das Ergebnis mit sich selbst).
a) x +2
b) 5x – 3
c) z : 2 + 8
d) 12 + 7 x
e) 18 – 3k
f) (y – 2) · 5
g) (n – 7)²
h) 5a² + 8
i) (6x + 4) : 2
j)
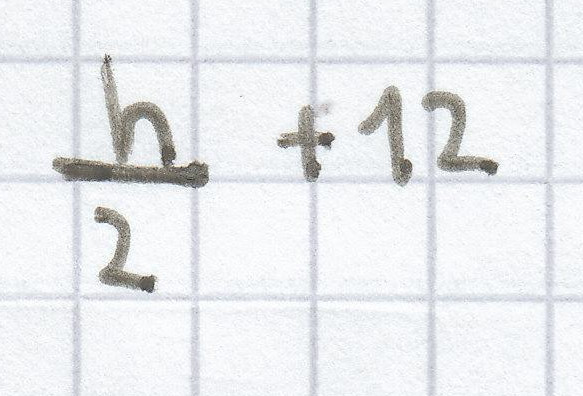
k)
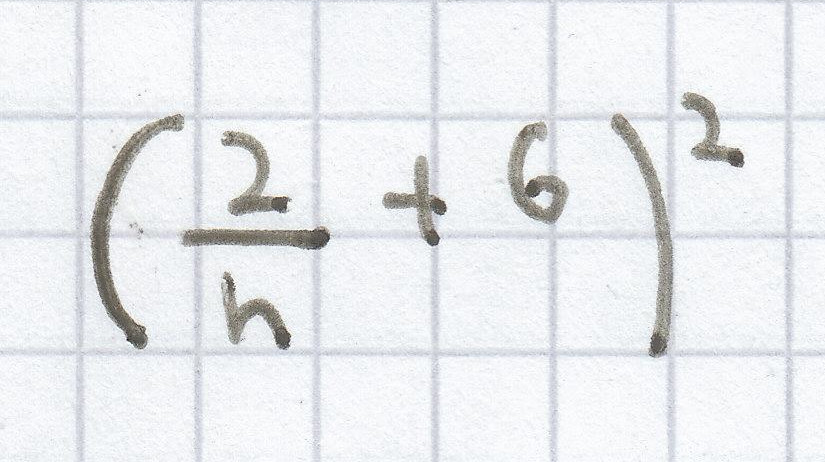
l) (x – 3)²
m) 5y³ + 7
3. Mathe-Nachhilfe-Aufgabe: Stelle zu folgenden Rechenvorschriften mit Variable den Term auf.
a) Addiere 9 zum Dreifachen einer Zahl.
b) Subtrahiere 12 vom Zehnfachen einer Zahl.
c) Multipliziere 7 mit einer Zahl und addiere zum Produkt 3.
d) Subtrahiere 12 von einer Zahl und multipliziere das Ergebnis mit sich selbst.
e) Addiere zum Quadrat einer Zahl ihren 5. Teil.
f) Quadriere eine um 5 vergrößerte Zahl.
g) Multipliziere eine Zahl mit
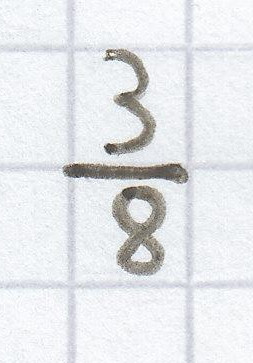
und addiere zum Produkt die 9.
h) Dividiere eine Zahl durch 5,3 und subtrahiere vom Quotienten 12.
i) Multipliziere eine Zahl mit der um 3 verkleinerten Zahl.
j) Dividiere das Dreifache einer Zahl durch 11 und subtrahiere vom Quotienten 4.
4. Mathematik-Nachhilfe-Aufgabe: Welches ist der „Irrläufer“-Term – einer ist nämlich keiner?!
a) 7 x – 3,
x · (x – 9),
14,
b + y,
9z – 5y²,
| | + 5 x,
(9 + t)³
b) x + 1,
(5 – 2z),
39,

,
5 + ²,
b,
–3k

Lösungen zum Mathematik-Stoffgebiet Term
1. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Ermittle den jeweiligen Wert des Terms bei den Zahlen 0, 1, 5, 10, 18 und 52 für x.
a) 0 in den Term eingesetzt, ergibt folgendes Ergebnis: 4 · 0 + 3 = 0 + 3 = 3,
für 1: 4 · 1 + 3 = 4 + 3 = 7,
für 5: 4 · 5 + 3 = 20 + 3 = 23,
für 10: 4 · 10 + 3 = 40 + 3 = 43,
für 18: 4 · 18 + 3 = 72 + 3 = 75,
für 52: 4 · 52 + 3 = 208 + 3 = 211
b) 0 in den Term eingesetzt, ergibt folgendes Ergebnis: 7 · 0 – 2 = 0 – 2 = –2,
für 1: 7 · 1 – 2 = 7 – 2 = 5,
für 5: 7 · 5 – 2 = 35 – 2 = 33,
für 10: 7 · 10 – 2 = 70 – 2 = 68,
für 18: 7 · 18 – 2 = 126 – 2 = 124,
für 52: 7 · 52 – 2 = 364 – 2 = 362
c) 0 in den Term eingesetzt, ergibt folgendes Ergebnis: 5 + (100 – 2 · 0) · 5 = 5 + (100 – 0) · 5 = 5 + 100 · 5 = 5 + 500 = 505,
für 1: 5 + (100 – 2 · 1) · 5 = 5 + (100 – 2) · 5 = 5 + 98 · 5 = 5 + 490 = 495,
für 5: 5 + (100 – 2 · 5) · 5 = 5 + (100 – 10) · 5 = 5 + 90 · 5 = 5 + 450 = 455,
für 10: 5 + (100 – 2 · 10) · 5 = 5 + (100 – 20) · 5 = 5 + 80 · 5 = 5 + 400 = 405,
für 18: 5 + (100 – 2 · 18) · 5 = 5 + (100 – 36) · 5 = 5 + 64 · 5 = 5 + 320 = 325,
für 52: 5 + (100 – 2 · 52) · 5 = 5 + (100 – 104) · 5 = 5 + (–4) · 5 = 5 + (–20) = –15
d) 0 in den Term eingesetzt, ergibt folgendes Ergebnis: (8 · 0 + 4) : 2 = (0 + 4) : 2 = 4 : 2 = 2,
für 1: (8 · 1 + 4) : 2 = (8 + 4) : 2 = 12 : 2 = 6,
für 5: (8 · 5 + 4) : 2 = (40 + 4) : 2 = 44 : 2 = 22,
für 10: (8 ·10 + 4) : 2 = (80 + 4) : 2 = 84 : 2 = 42,
für 18: (8 ·18 + 4) : 2 = (144 + 4) : 2 = 148 : 2 = 74,
für 52: (8 · 52 + 4) : 2 = (416 + 4) : 2 = 420 : 2 = 210
e) 0 in den Term eingesetzt, ergibt folgendes Ergebnis: (2 · 0 – 7)² = (0 – 7) ² = (–7)² = 49,
für 1: (2 · 1 – 7)² = (2 – 7)² = (–5)² = 25,
für 5: (2 · 5 – 7)² = (10 – 7)² = (3)² = 9,
für 10: (2 · 10 – 7)² = (20 – 7)² = (13)² = 169,
für 18: (2 ·18 – 7)² = (36 – 7)² = (29)² = 841, für 52: (2 · 52 – 7)² = (104 – 7)² = (97)² = 9409
2. Lösung zu der Mathe-Nachhilfe-Aufgabe: Wiedergabe der Rechenvorschrift eines Terms in Worten.
a) Addiere zu einer Zahl 2.
b) Multipliziere eine Zahl mit fünf und subtrahiere von dem Produkt 3.
c) Dividiere durch eine Zahl 2 und addiere zu dem Quotienten 8.
d) Addiere zu dem Produkt aus einer Zahl und 7 12.
e) Subtrahiere von 18 das Dreifache einer Zahl.
f) Subtrahiere zwei von einer Zahl und multipliziere das Ergebnis mit 5.
g) Subtrahiere 7 von einer Zahl und multipliziere das Ergebnis mit sich selbst.
h) Multiplizierte das Quadrat einer Zahl mit fünf und addiere zum Ergebnis 8.
i) Addiere zum Sechsfachen einer Zahl 4 und dividiere das Ergebnis durch 2.
j) Addiere 12 zur Hälfte einer Zahl.
k) Addiere 6 zum Quotienten aus 2 und einer Zahl und multipliziere das Ergebnis mit sich selbst.
l) Subtrahiere 3 von einer Zahl und multipliziere das Ergebnis mit sich selbst.
m) Addiere zum Fünffachen einer Zahl in der dritten Potenz sieben.
3. Lösung zu der Mathe-Nachhilfe-Aufgabe: Stelle den Term aus vorgegebener Rechenvorschrift und Variable auf.
a) 3x + 9
b) 10x – 12
c) 7x + 3
d) (x – 12) (x – 12) = (x – 12)²
e)
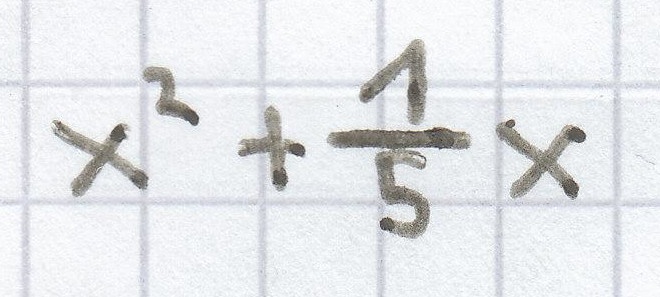
f) (x + 5)²
g)
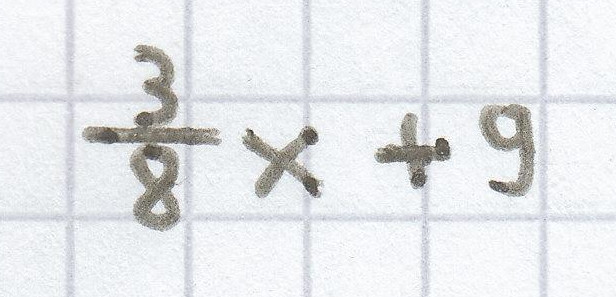
h) 5,3 : x – 12
i) (x – 3) · x
j) 11 : 3x – 4
4. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Welches ist der „Irräufer“-Term?
a) Der „falsche“ Term ist hier: | | + 5 x. Besteht ein Term aus Rechenzeichen, muss die mathematische Verknüpfung immer sinnvoll sein. Das ist bei leeren Betragszeichen, die zum Fünffachen einer Zahl addiert werden, nicht gegeben. Denn Betragszeichen machen immer nur Sinn, wenn auch darin etwas steht.
b) Der falsche Term ist hier: 5 + ². Auf ein Rechenzeichen, hier das „+“, darf in der Mathematik nie sogleich ein zweite Rechenzeichen, hier das „²“, folgen.