
Eines der beliebtesten Spiele bei Schülern ist Tic Tac Toe (das auch unter den Namen „Drei gewinnt“, „Kreuz und Kreis“, „XXO“ und vielen anderen bekannt ist). Es kann nahezu überall gespielt werden, die Regeln sind superleicht – und es macht irrsinnig viel Spaß. Hierzu braucht man nur ein Blatt Papier, einen Stift und zwei Spielwillige. In Nullkommanix ist das Spielfeld aus zwei Längsstrichen und zwei Querstrichen aufgezeichnet und schon kann es losgehen: Derjenige, der anfängt, macht ein X oder einen Kreis/O in eines der 9 Felder. Daraufhin kommt der Mitspieler an die Reihe. In den nun noch 8 freien Feldern muss dieser, je nachdem ob sein Gegenspieler mit einem X oder einem O begonnen hat, einen O oder ein X einzeichnen. Dann kommt wieder der Starter des Spiels dran. Gewonnen hat immer schließlich derjenige Spieler, der als erstes eine Längs- oder eine Diagonalreihe aus drei XXX oder drei OOO gebildet hat.
Aus Sicht der Mathematik gibt es nun 3 mögliche Ausgänge beziehungsweise Spiellösungen. Entweder der X-Setzer gewinnt oder der O-Setzer – oder keiner von beiden, da das Spiel unentschieden ausgeht. Und gerade diese letzte Spiellösung macht das Spiel so ungemein außergewöhnlich und so ungemein faszinierend. Egal ob Starter des Spiels oder Nicht-Starter, beim fehlerfreien Setzen jedes X und jedes O geht das Spiel immer garantiert unentschieden aus! Da beim Tic Tac Toe die möglichen Remis-Verläufe durch beide Spieler sehr leicht herbeigeführt werden können, ist das Spiel daher unstrittig „das fairste Spiel der Welt“. Schließlich gibt es dann keinen Gewinner und keinen Verlierer, also keinen, der besser ist oder schlechter – sondern immerzu nur eine harmonische Gleichheit.
Welche Spiellösungen führen aber immer zu einem Unentschieden? Rein von der Mathematik her scheint das nämlich erst einmal viel schwieriger zu realisieren zu sein. Denn aufgrund der 9 X-Setz-Möglichkeiten am Anfang, den 8 darauffolgenden O-Setzmöglichkeiten und den hierauf folgenden 7 X-Setzmöglichkeiten … bis hin zu der letzten 1-X-Setzmöglichkeit ergeben sich 362880 verschiedene Spielverläufe (da 9 Fakultät beziehungsweise 9! respektive 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9). Die Anzahl der Möglichkeiten verringert sich aber noch einmal stark, da oftmals bereits ein Gewinner feststeht, bevor alle 9 Felder ausgefüllt worden sind. Dadurch reduziert sich die Gesamtheit der Spielverläufe auf 255168. Aufgrund von Symmetrieverhältnissen kommen aber tatsächlich noch viel, viel weniger Spielmöglichkeiten zustande. Am Tic-Tac-Toe-Spielfeld liegen nämlich eine Punktsymmetrie und eine doppelte Achsensymmetrie vor. Deshalb kann das Spielfeld 4-mal gedreht werden und hierbei jeweils 1-mal gespiegelt werden. Das hat zur Folge, dass sich alle Spielverläufe noch einmal äußerst stark reduzieren, genauer gesagt um ein Achtel. Hierdurch ergeben sich schließlich 31896 mögliche Spielverläufe (255168 geteilt durch 8).
Da das Spiel, wie erwähnt, drei mögliche Ausgänge haben kann, verteilen sich alle möglichen Spielverläufe nun folgendermaßen: Bei 16398 Spielverläufen gewinnt Spieler 1, bei 9738 Spielverläufen gewinnt Spieler 2 und bei 5760 Spielverläufen endet das Spiel remis. Von den möglichen Ausgängen her gibt es zwar beim Tic Tac Toe beiderseitige Gewinner und Verlierer, halten aber Spieler 1 und Spieler 2 beim Setzen ihrer X und O konsequent bestimmte Setz-Muster ein, dann endet das Spiel immer unentschieden.
Ausgehend vom ersten Setzen eines Zeichens können nun beide Spieler durch Beibehalten dieser drei Remis-Setz-Muster ein Verlieren umgehen.
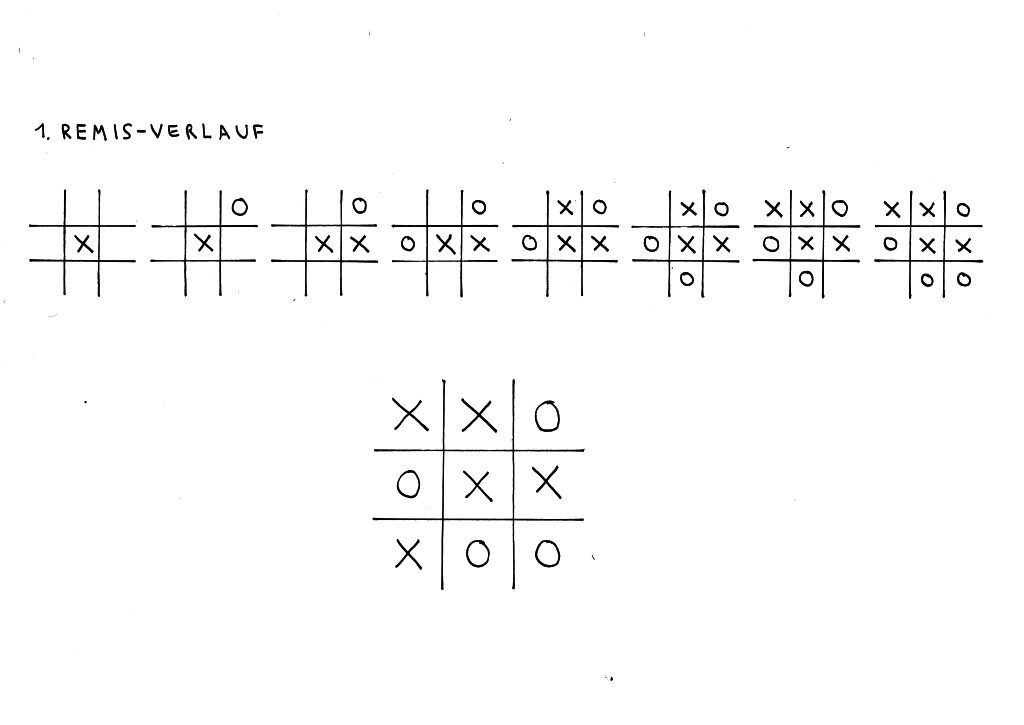
1. Remis-Setz-Muster:
Hier beginnt der 1. Spieler mit einem X in der Mitte. Der 2. Spieler muss seinen O an einen der vier Eckpunkte setzen. Dann kann das Spiel im Prinzip nur noch unentschieden ausgehen. 1. Remis-Verlauf beim Tic Tac Toe
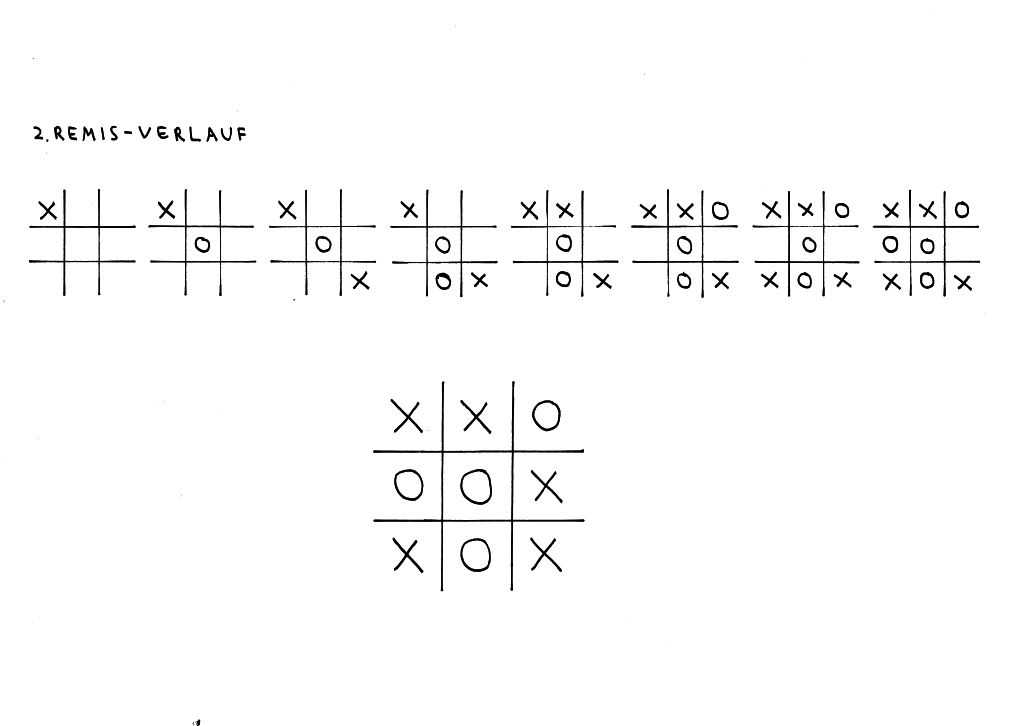
2. Remis-Muster:
Beim zweiten Remis-Muster beginnt der 1. Setzer an einem Eckfeld. Um hier ein Unentschieden zu erzielen, muss der 2. Spieler seinen O immer in das mittige Feld setzen – und nach dem 2. X-Setzer des Gegenspielers versuchen, ihn immer geschickt unter Druck zu setzen. Von allen drei möglichen Remis-Varianten ist das die Schwierigste.
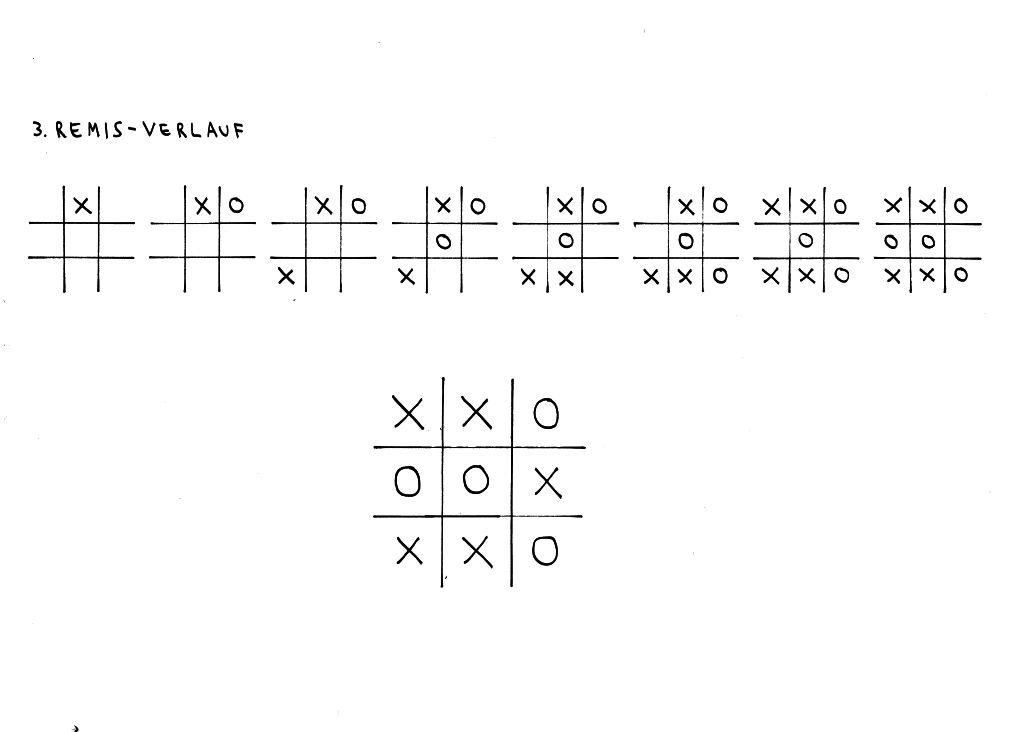
Das 3. Remis-Setzmuster:
Bei dem 3. Remis-Muster setzt der 1. Spieler sein X auf ein mittiges Außenfeld. Um ganz sicher zu gehen, dass man hier ein Remis erreicht, muss der 2. Spieler nur rechts oder links des gesetzten X seinen O setzen. Ebenso führen noch die Setz-Möglichkeiten des O in die Mitte sowie direkt gegenüber dem gesetzten X zu einem ungefährdeten Remis. 3. Remis-Verlauf beim Tic Tac Toe Weitere tolle Informationen zu Tic Tac Toe und den möglichen Unentschieden-Varianten findet man auch noch auf der Seite mathematische-basteleien.de.
Jedes Mal, wenn man nun mit seinen Klassenkameraden während der Schulstundenpausen oder ausgefallenen Mathe-Stunden Tic Tac Toe spielt, kann man sich nach jedem Spiel entspannt die Hand geben – für das beiderseitige erreichte Unentschieden. Kein Zorn wegen eines ärgerlichen Verlierens und keine übermäßige Freude aufgrund eines erreichten Sieges werden jemals bei Profi-Tic-Tac-Toern entstehen. Auch wenn man Tic Tac Toe unendlich oft spielen sollte, das fairste Spiel der Welt lässt bei fehlerfreien Zügen immer nur eines zu – salomonische Ausgänge, völlig ausgewogene Spielenden ohne jedwede Streitigkeiten.
