
„Wer hat uns das in Mathe denn bloß mit den Termen und Gleichungen eingebrockt?“ Diese reichlich nach Frust klingende Frage lässt sich zwar nicht dahingehend beantworten, dass nur eine einzige Person für das Kopfschmerzen verursachende Algebra verantwortlich gemacht werden kann, dennoch können hierfür klipp und klar mindestens drei „Hauptschuldige“ genannt werden. Eindeutig „schuldig“ beziehungsweise mitverantwortlich für heutzutage von Schülern zu lösende algebraische Aufgaben sind nämlich: Al-Chwarizmi (mit vollständigem Namen Abu Dscha’far Muhammad ibn Musa al-Chwarizmi genannt), François Viète und René Descartes.

Al-Chwarizmi, der in etwa 800 vor Christus unweit des Kaspischen Meeres und in Bagdad lebte, war ein arabischer Mathematiker und Universalgelehrter. Zum einen geht der Begriff Algebra auf ihn zurück, zum anderen hat er dieses sehr wichtige Teilgebiet der Mathematik entscheidend weiterentwickelt, da er als Erster lineare und quadratische Gleichungen geometrisch darstellte; François Viète, ein französischer Mathematiker und Jurist, der ab Ende der 70er Jahre im 16. Jahrhundert vorwiegend in Paris lebte, ist hauptverantwortlich für das Einführen von Buchstaben als Variable und für das Ersetzen vorher gängiger Rechenoperationen durch diese. Deshalb wird er auch des Öfteren „Vater der Algebra“ genannt; René Descartes, der mit dem „cogito ergo sum“ – „ich denke, also bin ich“ auch für eine der berühmtesten Sentenzen der Philosophie verantwortlich ist und der Ende des 16. Jahrhundert geboren ist, verbrachte große Teile seines Lebens in Frankreich und den Niederlanden. Dort war er als Mathematiker und Philosoph tätig. In der Mathematik „normierte“ er die Algebra entschieden weiter, indem er ganz bestimmte Buchstaben für Variable und Parameter festlegte und die heutige Potenz- und Wurzelschreibweise einführte. Zudem trägt René Descartes die Hauptverantwortung beziehungsweise aus vielfacher Schülersicht die Hauptschuld daran, dass es bei Gleichungen eine sogenannte Normalform gibt – und um diese sich weitere vielfach kopfzerbrechende algebraische Aufgaben drehen.
Aber keine Sorge! Bei dieser Mathe-Nachhilfe-„Stunde“ geht es „nur“ um Terme.
Aufgaben zum Mathematik-Stoffgebiet Term
1. Mathematik-Nachhilfe-Aufgabe: Löse bei jedem Term alle Klammern mittels des Distributivgesetzes/Verteilungsgesetzes auf.
a) 5 · (a – b)
(a – b) · 12
–3 · (a – b)
b) x · (x – 5)
8 · (–x² + 15)
(x – 9) · (–y)
c) –6 · (r – 9)
(–r – s) · 18
(– r) · (– r – 7)
2. Mathematik-Nachhilfe-Aufgabe: Zeige, wie fit du beim Ausmultiplizieren wirklich bist.
a) 9ab · (7a + 4b)
(5a – 12b) · (–5a)
(–15a) · (–6b –11a)
b) (5x²y – 9xy²) · 2x²y
5ab · (–b² – a³)
(15 – 3s²) · 7rs²
c) (2a + b) · (–8ab²)
(8x – 3y) · (21x³y²)
(–s – r³) · (–34rs²)
3. Mathe-Nachhilfe-Aufgabe: Zeige noch einmal dein Können beim Ausmultiplizieren und beim Vereinfachen eines Terms.
a) 9 (2x – y) – 7y – 9x
–12s + 2r (7 – s) – 5rs
5 (2a – 3b) + (5a – 11b) 8
b) –12s + 19r + 3,2 (12s – 7r)
14 (2,4x – 9,5y) – 3x + 5y
5 (7,4a – 5,2b) – 6 (3,2b – 3,8a)

Lösungen zu dem Mathe-Stoffgebiet Term
1. Lösung zu der Mathe-Nachhilfe-Aufgabe: Wende zum Auflösen der Klammern jeweils das Distributivgesetz/Verteilungsgesetz an.
a) 5 · (a – b) = 5 · a + 5 · (–b) = 5a – 5b.
Das ist der Endterm. Achte bei der Klammer, dass das Minus mit ausmultipliziert wird. Klammer den Minusterm immer am besten komplett mit Vorzeichen ein, da es zum Einzelterm mit dazu gehört.
(a – b) · 12 = a · 12 + (–b) · 12 = 12a – 12b
Weiter kann der Term nicht vereinfacht werden.
–3 · (a – b) = (–3) · a + (–3) · (–b) = –3a + 3b.
Achte hier wiederum ganz besonders beim Ausmultiplizieren des zweiten Einzelterms auf die Vorzeichenregel, dass nämlich „–“ · „–“ = „+“ wird.
b) x · (x – 5) = x · x + x · (– 5) = x² – 5x
Das ist der Endterm. Achte hier zusätzlich darauf, dass bei der Multiplikation gleicher Variablen die Potenzen addiert werden.
8 · (–x² + 15) = 8 · –x² + 8 · 15 = –8x² +120
Das ist der Endterm.
(x – 9) · (–y) = x · (–y) + (–9) · (–y) = –xy + 9y
Weiter kann der Term nicht vereinfacht werden.
c) –6 · (r – 9) = –6 · r + (–6) · (– 9) = –6r + 54
Das ist der Endterm.
(–r – s) · 18 = (–r) · 18 + (–s) · 18 = –18r –18s
Weiter kann der Term nicht vereinfacht werden.
(– r) · (– r – 7) = (–r) · (–r) + (– r) · (–7) = r² + 7r
Das ist der Endterm.
2. Lösung zu der Mathe-Nachhilfe-Aufgabe: Zeige, wie gut deine Fähigkeiten beim Ausmultiplizieren sind.
a) 9ab · (7a + 4b) = 9ab · 7a + 9ab · 4b = 63a²b + 36ab²
Weiter kann der Term nicht mehr vereinfacht werden. Beachte hier, dass a · a = a² sowie b · b = b² wird.
(5a – 12b) · (–5a) = 5a · (–5a) + (–12b) · (–5a) = –25a² + 60ab
Weiter kann auch hier der Term dann nicht mehr vereinfacht werden. Beachte hier, dass das Minus in der ersten Klammer beim Ausmultiplizieren nicht vergessen wird und dass „–“ · „–“ = „+“ wird.
(–15a) · (–6b –11a) = (–15a) · (–6b) + (–15a) · (–11a) = 90ab + 165a²
Das ist der Endterm. Beachte hier wiederum, dass das zweite Minuszeichen in der zweiten Klammer nicht vergessen wird und dass die Vorzeichenregel bei der Multiplikation richtig angewendet wird.
b) (5x²y – 9xy²) · 2x²y = 5x²y · 2x²y + (–9xy²) · 2x²y =
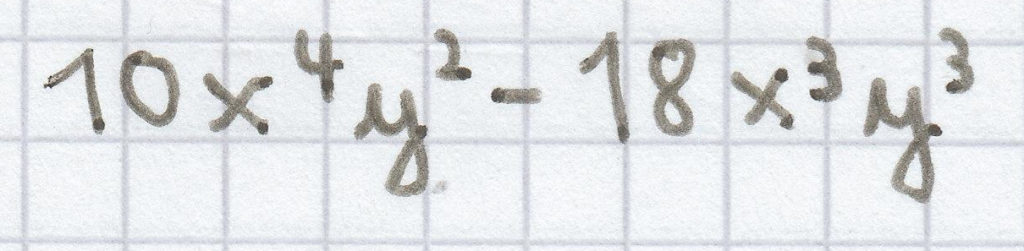
Das ist der Endterm. Achte besonders bei der Multiplikation gleicher Variablen auf die richtige Addition der Potenzen.
5ab · (–b² – a³) = 5ab · (–b²) + 5ab · (–a³) =

Weiter kann der Term nicht vereinfacht werden.
(15 – 3s²) · 7rs² = 15 · 7rs² + (–3s²) · 7rs² =
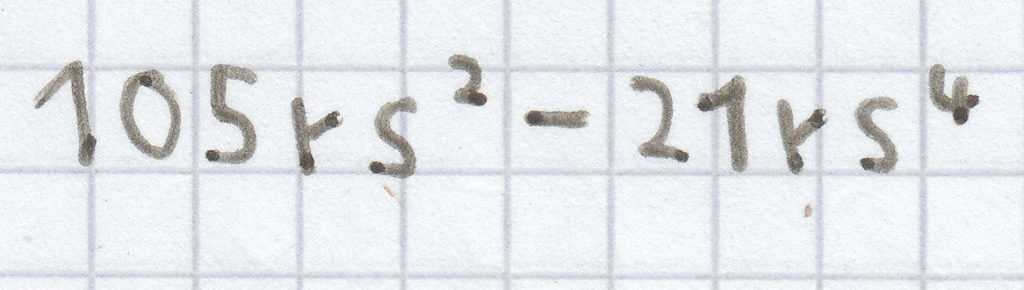
Das ist der Endterm. Beachte besonders, dass beim Ausmultiplizieren des zweiten Einzelterms die Addition der Potenzen richtig durchgeführt wird.
c) (2a + b) · (–8ab²) = 2a · (–8ab²) + b · (–8ab²) =
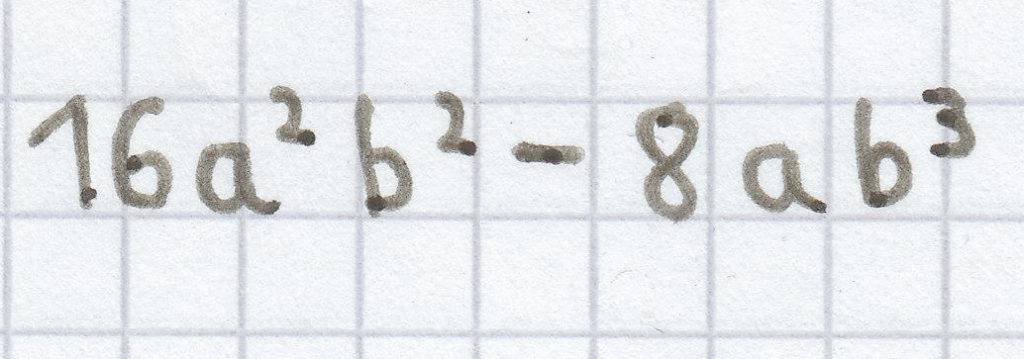
Weiter kann der Term nicht vereinfacht werden.
(8x – 3y) · (21x³y²) = 8x · 21x³y² + (–3y) · 21x³y² =
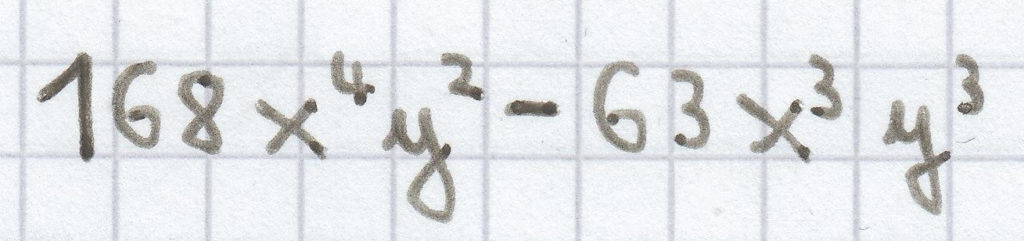
Das ist der Endterm.
(–s – r³) · (–34rs²) = (–s) · (–34rs²) + (–r³) · (–34rs²) =
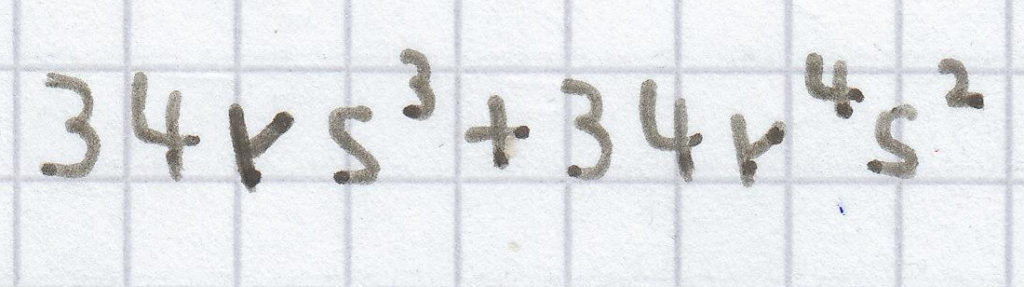
Das ist der Endterm.
3. Lösung der Mathematik-Nachhilfe-Aufgabe: Multipliziere aus und fasse den Term so weit wie möglich zusammen.
a) 9 (2x – y) – 7y – 9x = 9 · 2x + 9 · (– y) – 7y – 9x = 18x – 9y – 7y – 9x = 9x – 16y
Weiter kann der Term nicht vereinfacht werden.
–12s + 2r (7 – s) – 5rs = –12s + 2r · 7 + 2r · (–s) – 5rs = –12s + 14r – 2rs – 5rs = –12s + 14r – 7rs
Das ist der Endterm.
5 (2a – 3b) + (5a – 11b) 8 = 5 · 2a + 5 · (–3b) + 5a · 8 + (–11b) · 8 = 10a –15b + 40a – 88b = 50a – 103b
Weiter kann der Term nicht vereinfacht werden.
b) –12s + 19r + 3,2 (12s – 7r) = –12s + 19r + 3,2 · 12s + 3,2 · (–7r) = –12s + 19r + 38,4s – 22,4r = 26,4s – 3,4r
Das ist der Endterm.
14 (2,4x – 9,5y) – 3x + 5y = 14 · 2,4x + 14 · (–9,5y) – 3x + 5y = 33,6x – 133y – 3x + 5y = 30,6x – 128y
Das ist der Endterm.
5 (7,4a – 5,2b) – 6 (3,2b – 3,8a) = 5 · 7,4a + 5 · (–5,2b) + (–6) · 3,2b + (–6) · (–3,8a) = 37a – 26b – 19,2b + 22,8a = 59.8a – 45,2b
Weiter kann der Term nicht vereinfacht werden.