
In jedem Raum in einem häuslichen Wohnfeld (es sei denn, man wohnt im Dachgeschoss) begegnet man dem Satz des Pythagoras – und das von Zimmer zu Zimmer gleich doppelt. Normalerweise besitzen ja Räume in Wohnungen eine rechteckige Grundfläche und demzufolge auch die Form eines viereckigen Quaders. Jeder viereckige Quader beziehungsweise Raum enthält nun 2-mal den Satz des Pythagoras – auf der Grundfläche in Form der Flächendiagonalen und im Zimmer selbst in Form der Raumdiagonalen. Hat man daher die Länge und die Breite des Raumes gemessen, dann kann man zunächst über den Satz des Pythagoras die Flächendiagonale des Zimmers berechnen und im Anschluss unter Einbeziehung der Raum-Höhe die Raumdiagonale. Die jeweils ermittelten Ergebnisse lassen dann vielleicht das Zimmer größer erscheinen und man bekommt dadurch eventuell ein positiveres Raumgefühl (das war natürlich eher scherzhaft gemeint 🙂 ).

In früheren Lehmhütten oder adligen Häusern war der Satz des Pythagoras übrigens bei Weitem nicht so oft in „doppelter Ausführung“ anzutreffen, wie das heutzutage in jeder gängigen Wohnung der Fall ist. Lehmhütten zeichneten sich nämlich oftmals gerade darin aus, dass alle Seitenlängen des Raumes (Länge, Breite und Höhe) schief waren – und hierdurch der Satz des Pythagoras gewissermaßen ausgesperrt wurde. Bei adeligeren Residenzen kam es hingegen häufig vor, dass zumindest ein Raum eine halbrunde oder runde Grundfläche hatte oder ein Gewölbe vorwies – und somit auch hier der Satz des Pythagoras unerwünscht war.
Aufgaben zum Mathe-Stoffgebiet: der Satz des Pythagoras
1. Mathematik-Nachhilfe-Aufgabe: Stelle fest, ob das jeweilige Dreieck ABC rechtwinklig ist oder nicht. Falls nicht, gebe an, ob es sich um ein stumpfwinkliges oder ein spitzwinkliges Dreieck handelt.
a) a = 8 cm, b = 6 cm, c = 10 cm
b) a = 4 cm, b = 3 cm, c = 5 cm
c) a = 9 cm, b = 7 cm, c = 11 cm
d) a = 4 cm, b = 6 cm, c = 8 cm
e) a = 17 dm, b = 23 dm, c = 29 dm
f) a = 5 m, b = 13 m, c = 12 m
g) a = 9 cm, b = 8 cm, c = 70 mm
2. Mathe-Nachhilfe-Aufgabe: Gegeben ist ein gleichschenkliges Dreieck, das die Basis c hat und a als eine Seitenlänge des Schenkels. Welche Beziehung muss zwischen der Basis c und der Seitenlänge a gegeben sein, dass gilt:
a) das Dreieck ist rechtwinklig
b) das Dreieck ist stumpfwinklig
c) das Dreieck ist spitzwinklig
3. Mathematik-Nachhilfe-Aufgabe: In einem Zimmer, das die Form eines rechtwinkligen Quaders hat, beträgt die Länge 4 m, die Breite 2 m und die Höhe 3 m. Wie groß ist die Flächendiagonale und die Raumdiagonale des Zimmers?

Lösung zum Mathe-Stoffgebiet: der Satz des Pythagoras
1. Mathematik-Nachhilfe-Aufgabe: Überprüfe, um welche Dreiecke es sich jeweils handelt.
Die Umkehrung vom Satz des Pythagoras besagt ja, dass ein Dreieck rechtwinklig ist, wenn die Summe der quadrierten kleineren Seitenlängen gleich der größten Seitenlänge ist. Ist dies der Fall, dann sind die beiden kleineren Seitenlänge die beiden Katheten und die größere Seitenlänge die Hypotenuse des rechtwinkligen Dreiecks. Geht diese aufgestellte Flächengleichung nicht auf und die Summe der beiden quadrierten kleineren Seitenlängen ist größer als die quadrierte größere Seitenlänge, dann ist das Dreieck spitzwinklig. Das Dreieck ist hingegen stumpfwinklig, wenn die Summe der beiden quadrierten kleineren Seitenlängen kleiner ist als das Ergebnis der quadrierten größeren Seitenlänge. Das muss man nun bei jeder Aufgabe überprüfen!
a) a = 8 cm, b = 6 cm, c = 10 cm
(8 cm)² + (6 cm)² = (10 cm)²
64 cm² + 36 cm² = 100 cm²
100 cm² = 100 cm²
Da hier bei der Gleichung eine „wahre“Aussage herauskommt, ist das vorliegende Dreieck rechtwinklig.
b) a = 4 cm, b = 3 cm, c = 5 cm
(4 cm)² + (3 cm)² = (5 cm)²
16 cm² + 9 cm² = 25 cm²
25 cm² = 25 cm²
Hier ergibt sich ebenfalls eine „wahre“Aussage. Daher handelt es sich auch hier um ein rechtwinkliges Dreieck.
c) a = 9 cm, b = 7 cm, c = 11 cm
(9 cm)² + (7 cm)² = (11 cm)²
81 cm² + 49 cm² = 121 cm²
130 cm² = 121 cm²
Hier zeigt sich, dass die Gleichung nicht wahr ist, da die quadrierten kleineren Seitenlängen größer der quadrierten größeren Seitenlänge sind bzw. 130 cm² > 121 cmi²ist. Daher liegt hier ein spitzwinkliges Dreieck vor.
d) a = 4 cm, b = 6 cm, c = 8 cm
(4 cm)² + (6 cm)² = (8 cm)²
16 cm² + 36 cm² = 64 cm²
52 cm² = 64 cm²
Hier ergibt sich, dass die die Summe der quadrierten kleineren Seitenlängen kleiner ist als das Ergebnis der quadrierten größeren Seitenlänge. Deshalb ist das hier vorliegende Dreieck ein stumpfwinkliges.
e) a = 17 dm, b = 23 dm, c = 29 dm
(17 dm)² + (23 dm)² = (29 dm)²
289 dm² + 529 dm² = 841 dm²
818 dm² = 841 dm²
Hier zeigt sich, dass die Summe der quadrierten kleineren Seitenlängen kleiner ist als das Ergebnis der quadrierten größeren Seitenlänge. Folglich ist das hier vorliegende Rechteck wiederum ein stumpfwinkliges.
f) a = 5 m, b = 13 m, c = 12 m
Bei dieser Aufgabe sieht man sofort, dass die Seitenlänge b die größte ist. Daher ergibt sich hier folgende Flächengleichung.
(5 m)² + (12 m)² = (13 m)²
25 m² + 144 m² = 169 m²
169 m² = 169 m²
Da hier die Gleichung eine „wahre“Aussage liefert, ist das vorliegende Dreieck ein rechtwinkliges.
g) a = 9 cm, b = 8 cm, c = 70 mm
Bevor man hier die Flächengleichung aufstellen kann, muss man zuerst die Längeneinheiten angleichen. Da bereits zwei Seitenlängen die Längeneinheit Zentimeter (cm) vorweisen, geht es am schnellsten die dritte von Millimeter (mm) in Zentimeter umzurechnen (c = 70 mm geteilt durch 10 = 7 cm)
Auch muss man hier wiederum beachten, dass die Seitenlänge a die größte ist. Folglich ergibt sich hier diese Flächengleichung.
(8 cm)² + (7 cm)² = (9 cm)²
64 cm² + 49 cm² = 81 cm²
113 cm² = 81 cm²
Da hier die Summe der quadrierten kleineren Seitenlängen größer ist als das Ergebnis der quadrierten größeren, ist das Dreieck ein spitzwinkliges.
2. Mathematik-Nachhilfe-Aufgabe: Welche Beziehung muss in einem gleichschenkligen Dreieck mit der Basis c und dem Schenkel a bestehen, damit Folgendes gilt:
a) das Dreieck ist rechtwinklig
b) das Dreieck ist stumpfwinklig
c) das Dreieck ist spitzwinklig
Bei einem gleichschenkligen Dreieck sind, wie der Name es schon sagt, die beiden Schenkel gleich groß und demzufolge gilt auf diese Aufgabe bezogen: die eine Seitenlänge a des Dreiecks ist gleich der anderen Seitenlänge a des Dreiecks. Folglich ergibt sich diese Flächengleichung.
(c)² = (a)² + (a)²
c² = a² + a²
c² = 2a²
Zieht man nun die Wurzel, dann kann man diese algebraischen Vereinfachungen machen und es ergibt sich schließlich diese Endgleichung.
c² = 2a² | √
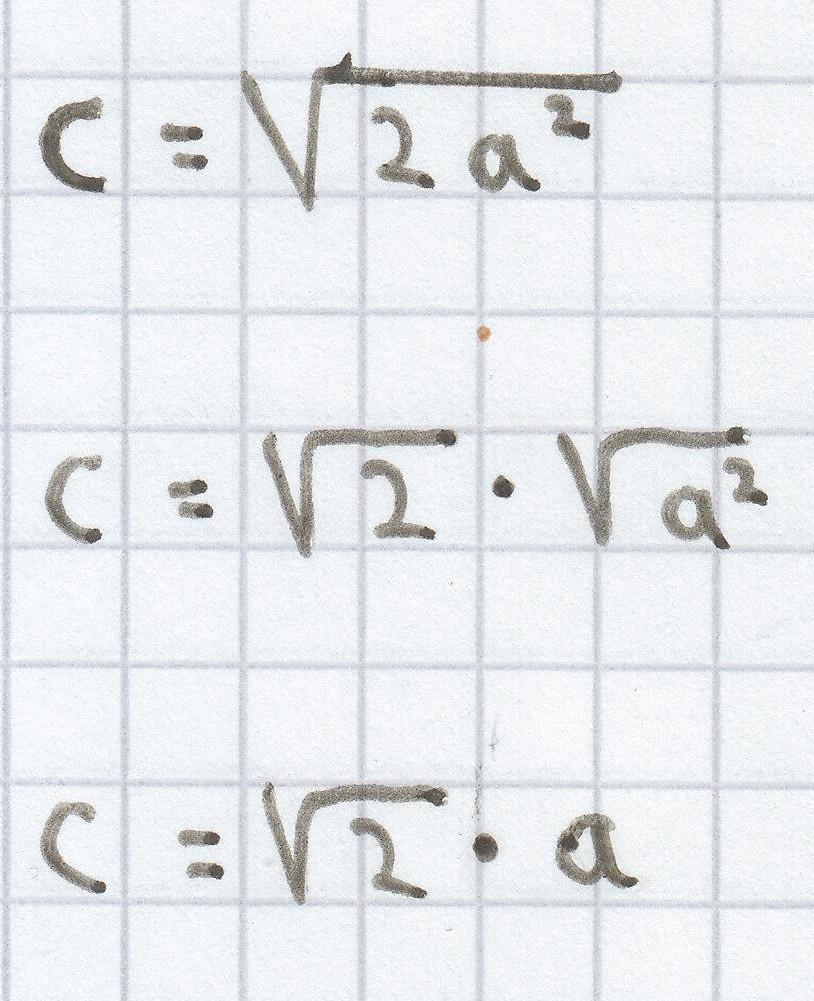
Gilt nun, dass
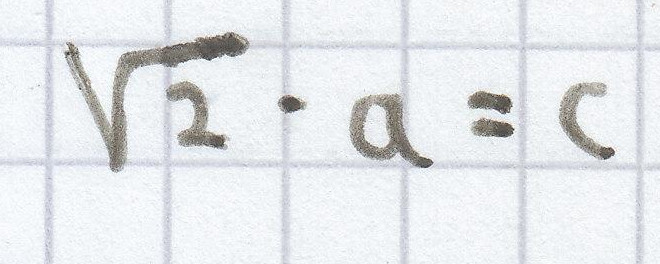
ist, dann ist das gleichschenklige Dreieck rechtwinklig, da die Gleichung „wahr“ ist.
Gilt nun, dass

ist, dann ist das gleichschenklige Dreieck stumpfwinklig.
Gilt nun, dass
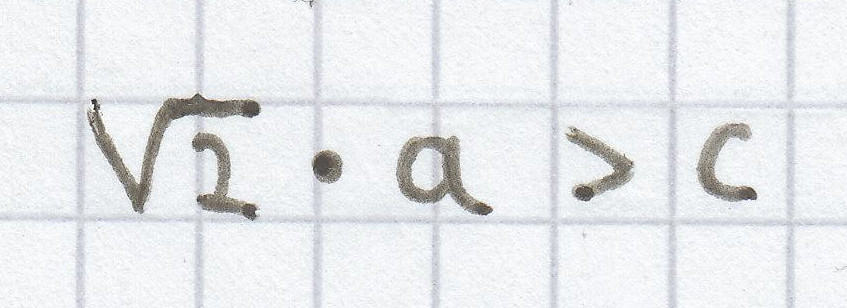
ist, dann ist das gleichschenklige Dreieck spitzwinklig.
Formt man die Gleichung nach dem Schenkel a um, dann ergibt sich folgende Beziehung zur Basis c.
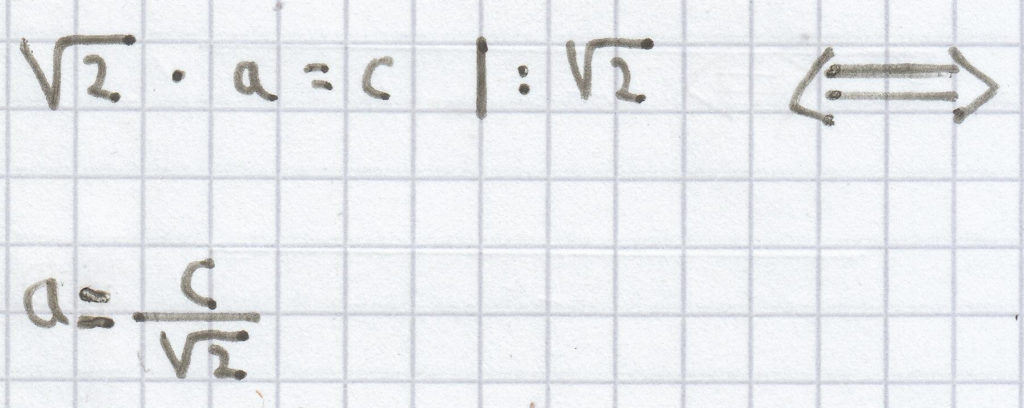
a) Gilt nun, dass
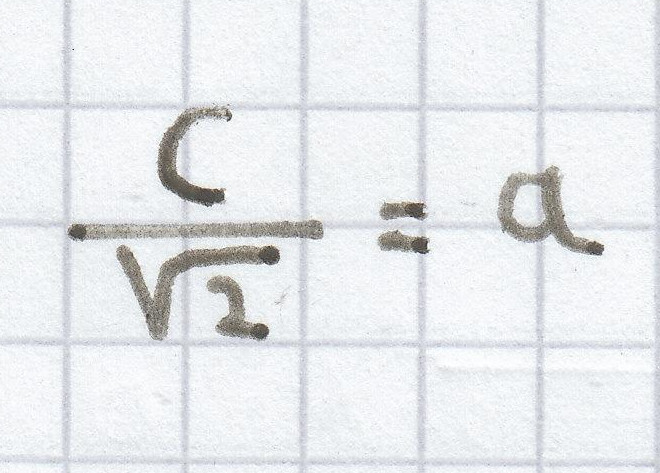
ist, dann ist das gleichschenklige Dreieck wiederum rechtwinklig.
b) Gilt nun, dass
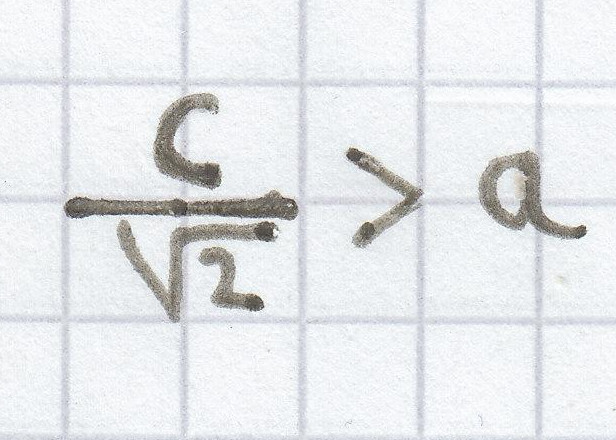
ist, dann ist das gleichschenklige Dreieck wiederum stumpfwinklig.
c) Gilt nun, dass
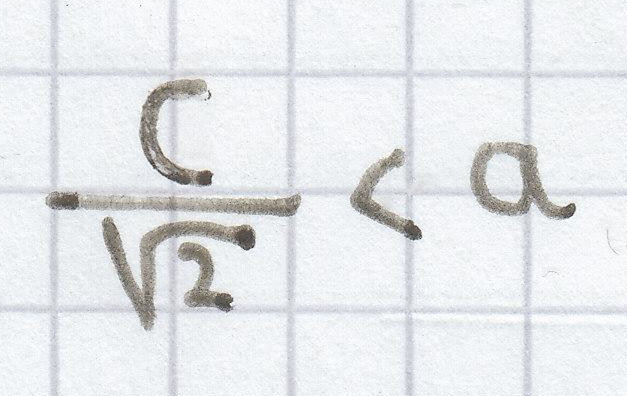
Bedingung für Spitzwinkligkeit bei gleichschenkligem Dreieck
ist, dann ist das gleichschenklige Dreieck wiederum spitzwinklig.
3. Mathe-Nachhilfe-Aufgabe: Wie groß ist die Flächendiagonale und die Raumdiagonale in einem Zimmer, das die Länge 4 m, die Breite 2 m und die Höhe 3 m hat?
Bevor man mit den Berechnungen anfängt, fertigt man am besten eine Skizze, um genau die Beziehungen sehen zu können, in denen der Satz des Pythagoras auftritt.
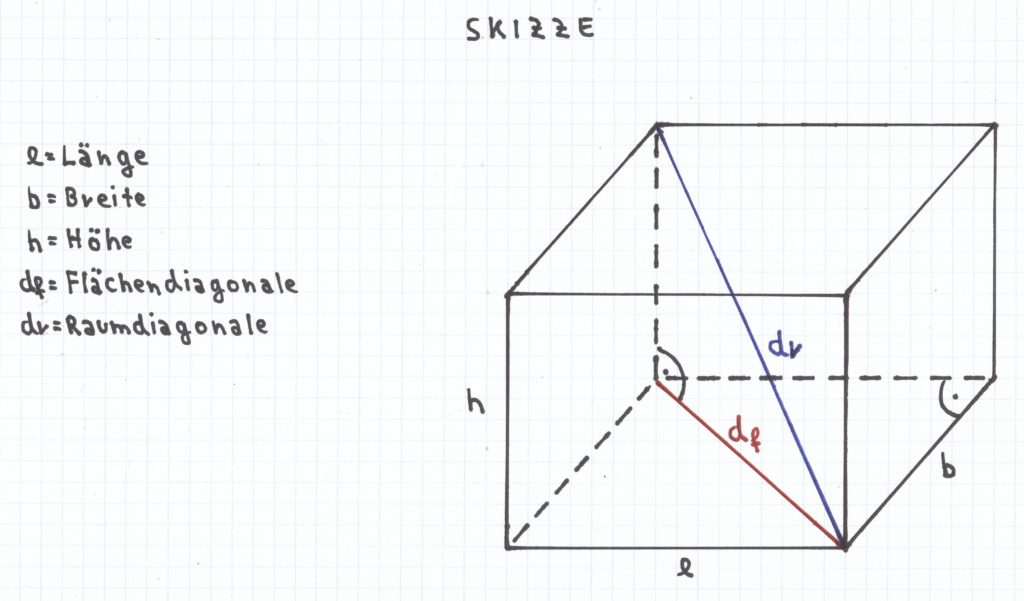
Wie man anhand der Skizze sehen kann, ist die Flächendiagonale diejenige Diagonale, die zwischen der Länge und der Breite auftritt.
Natürlich hätte man aber auch zwischen der Länge und der Höhe sowie der Breite und der Höhe eine Flächendiagonale einzeichnen können, da diese Größen ja ebenfalls in einem Raum jeweils eine Fläche bilden. Hierbei bilden die Länge und die Breite eine rechten Winkel. (Das Gleiche gilt bei der Fläche zwischen Länge und Höhe sowie Breite und Höhe.)
Aufgrund des Verzerrungswinkels von 45º, unter dem die Breite eingezeichnet wurde, zeigt sich das bei der Skizze aber nur, indem man das Symbol für den rechten Winkel einzeichnet (der Kreisausschnitt mit Punkt in der Mitte).
Da die Flächendiagonale immer die Hypotenuse des rechtwinkligen Dreiecks ist, kann man diese in diesem Beispiel folgendermaßen berechnen.
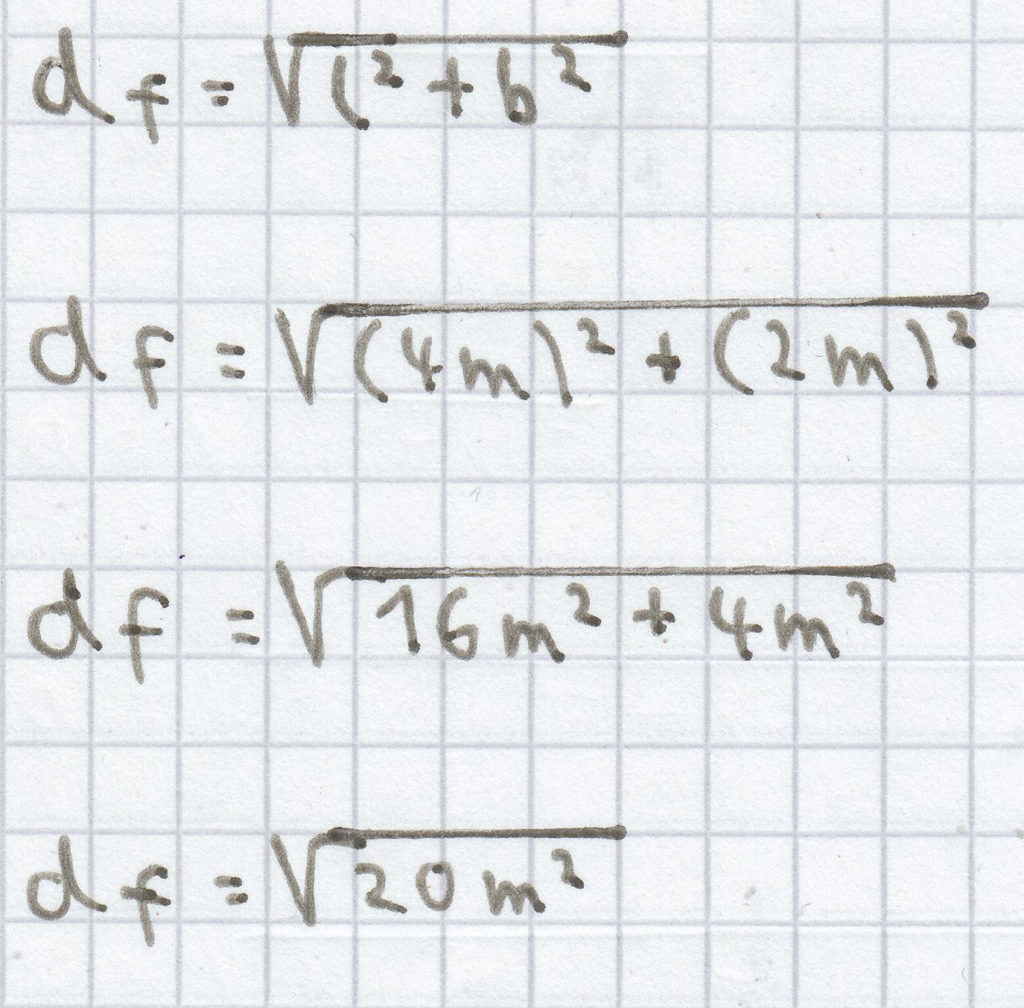
df = 4,47 m (gerundet auf zwei Nachkommastellen)
Die Flächendiagonale beträgt hier 4,47 m.
Wie man wiederum anhand der Skizze sehen kann, bildet die Flächendiagonale zusammen mit der Höhe ein rechtwinkliges Dreieck, in der die Raumdiagonale die Hypotenuse ist. Aufgrund der verzerrten Darstellung kann man dieses rechtwinklige Dreieck wiederum nur an dem Kreisausschnitt mit Punkt in der Mitte erkennen.
Hätte man eine Flächendiagonale genommen, die sich aus Länge und Höhe zusammengesetzt hätte, dann hätte die Flächendiagonale mit der Breite ein rechtwinkliges Dreieck gebildet, wobei wiederum die Hypotenuse die Raumdiagonale gewesen wäre. Bei der Zusammensetzung der Flächendiagonale aus Breite und Höhe verhält es sich ebenso. Denn hierbei würde die Flächendiagonale mit der Länge ein weiteres rechtwinkliges Dreieck bilden, bei dem erneut die Hypotenuse die Raumdiagonale wäre.
Demzufolge ergibt sich die Gleichung zur Berechnung der Raumdiagonalen.
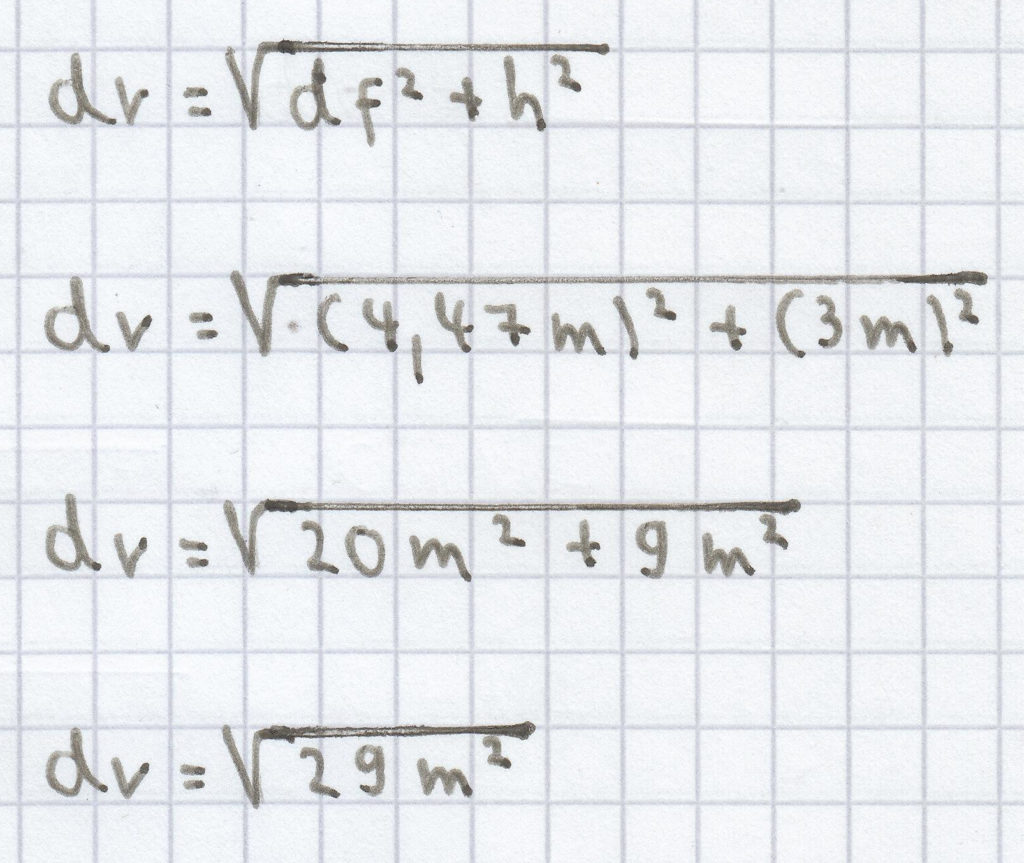
dr = 5,39 m (gerundet auf zwei Nachkommastellen)
Die Raumdiagonale beträgt hier 5,39 Meter.
Hat man bei einer Aufgabe Länge, Breite und Höhe eines quaderförmigen Raumes gegeben, so ist die Flächendiagonale immer die Hypotenuse aus einer der beiden Größen. Die Raumdiagonale ist hierbei ebenfalls immer die Hypotenuse, wobei eine Kathete die Fächendiagonale ist und die andere Kathete die noch verbleibende Größe des quaderförmigen Raumes.