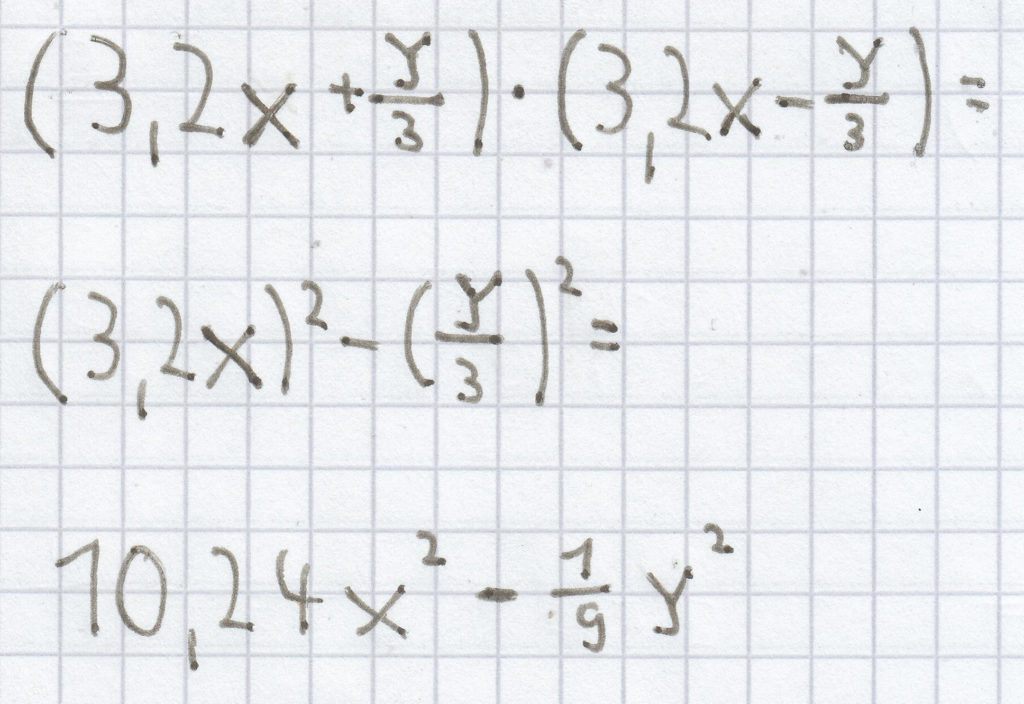
Binomische Formeln korrekt auflösen zu können, ist das eine, das andere ist zu erkennen, dass überhaupt eine binomische Formel vorliegt. Denn hin und wieder müssen vorab erst bestimmte algebraische Umformungen vorgenommen werden, um klipp und klar zu sehen – dass eine binomische Formel vorliegt und um welche genau es sich hierbei handelt. Darauf kann man diese schließlich nach dem oft geübten Schema auflösen. Folgende Beispiele sollen hierbei den Schülerinnen und Schülern helfen – um einen besseren „Binomischen-Formel-Blick/Durchblick“ zu bekommen:
Beispiel 1: (–3 + 7x)²
Hier sieht es zunächst so aus, als ob keine binomische Formel vorliegen würde, da der erste Einzelterm in der Klammer ein Minus vorweist. Da jedoch innerhalb der Klammer eine algebraische Summe vorliegt, darf man dort das Kommutativgesetz/Vertauschungsgesetz anwenden:
Beispiel 1: (–3 + 7x)² = (7x – 3)²
Wie man nun klipp und klar sieht, liegt hier eindeutig die 2. Binomische Formel vor. Deshalb gilt hier folgendes Auflösungsschema:
Beispiel 1: (–3 + 7x)² = (7x – 3)² = (7x)² – 2 · 3 · 7x + (3)² = 49x² – 42x + 9
Hiermit wäre die 2. Binomische Formel korrekt aufgelöst.
Beispiel 2: (–4x – 7)²
Auf den ersten Blick sieht es wiederum so aus, als würde hier keine binomische Formel vorliegen, da beide Einzelterme ein Minus vorweisen. Um einen besseren Blick/Durchblick zu haben, dass es hier dennoch um eine binomische Formel handelt, löst man am besten die Potenz zu einem Produkt auf.
Beispiel 2: (–4x – 7)² = (–4x – 7) · (–4x – 7)
Hier darf man nun bei beiden Klammern den Faktor –1 ausklammern, wobei sich dann natürlich jeweils die Vorzeichen der Einzelterme in der Klammer „umdrehen“:
Beispiel 2: (–4x – 7)² = (–4x – 7) · (–4x – 7) = (–1) · (4x + 7) · (–1) · (4x + 7)
Dadurch, dass man beide „–1“-Faktoren miteinander malnehmen darf, ergibt sich hieraus: „–1“ · „–1“ = „1“ – und es bleiben nur noch die beiden Klammern übrig. Und in der Potenzschreibweise ergibt sich dadurch klipp und klar die 1. Binomische Formel:
Beispiel 2: (4x +7) · (4x + 7) = (4x + 7)²
Daher gilt hier folgendes Auflösungsschema:
Beispiel 2: (4x + 7)² = (4x)² + 2 · 4x · 7 + (7)² = 16x² + 56x + 49
Natürlich macht ist es vor allem aus Zeitgründen nicht wirklich Sinn, diese recht umfangreiche algebraische Umformung stets durchzuführen. Deshalb sollte man sich einfach als „Binomischen-Formel-Zusatz“ merken, dass bei einem „doppelten“ Minus bei den Einzeltermen immer die 1. Binomische Formel vorliegt!
Beispiel 3: (–3x + 2y) · (–3x – 2y)
Zunächst sieht es erneut so aus, als würde keine binomische Formel hier vorliegen. Durch Ausklammern von „–1″ bei beiden Klammern wird jedoch Folgendes offenbar:
Beispiel 3: (–3x + 2y) · (–3x – 2y) = (–1) · (3x – 2y) · (–1) · (3x + 2y)
Da „–1″ · „–1″ zu „1″ wird, erhält man diesen Term:
Beispiel 3: (3x – 2y) · (3x + 2y)
Bei einem Produkt gilt wie bei einer Summe das Kommutativgesetz/Vertauschungsgesetz, weshalb man die beiden Faktoren (hier die beiden Klammern) des Produktes vertauschen darf – und wie man augenscheinlich sieht, kommt dann eindeutig die 3. Binomische Formel zum Vorschein:
Beispiel 3: (3x – 2y) · (3x + 2y) = (3x + 2y) · (3x – 2y)
Daher gilt hier dieses Auflösungsschema:
Beispiel 3: (3x + 2y) · (3x – 2y) = (3x)² – (2y)² = 9x² – 4y²
Hier macht es Sinn, das „Minus 1″ jeweils auszuklammern, da man dann sofort der 3. Binomischen Formel gewahr wird – und sogleich mit dem bekannten Auflösungsschema der 3. Binomischen Formel die aufgelöste Form erhält.
Wenn man sich sehr schwer tut zu erkennen, dass eine binomische Formel vorliegt, dann kann man übrigens auch immer den etwas strapaziöseren Weg über das Distributivgesetz gehen. Beim fehlerfreien Anwenden wird das Ergebnis nämlich absolut das Gleiche sein wie bei einem der Auflösungsschemata der binomischen Formeln!
Aufgaben zum Mathematik-Stoffgebiet Binomische Formeln
1. Mathe-Nachhilfe-Aufgabe: Zeige, dass eine binomische Formel vorliegt und löse dies anschließend auf!
a)
(–8 + x)²
(a + (–3))²
(7 – (–b))²
(–8 – x)²
b)
(a + (–b))²
(–x – y)²
(–y + x)²
(–a + (–b))²
c)
(3a + (–5b))²
(–7a + b)²
(–9x – 3y)²
(–2a – (–5b))²
d)
(4r + 9s) · (–4r + 9s)
(–8x + 5y)²
(2a – 6b) · (2a + 6b)
(–x + 6y) · (–x – 6y)
2. Mathe-Nachhilfe-Aufgabe: Zeige, wie gut du bereits einfach zu erkennende binomische Formeln auflösen kannst.
a)
(7a + 9)²
(9s + 3t)²
(0,8u – 6)²
b)
(12x + 8y)²
(7k – 3)²

c)
(3,6 + a)²
(x + 7,8) (x – 7,8)
(y – 1,5)²
d)
(7a – 15)²
(14x – 20)²
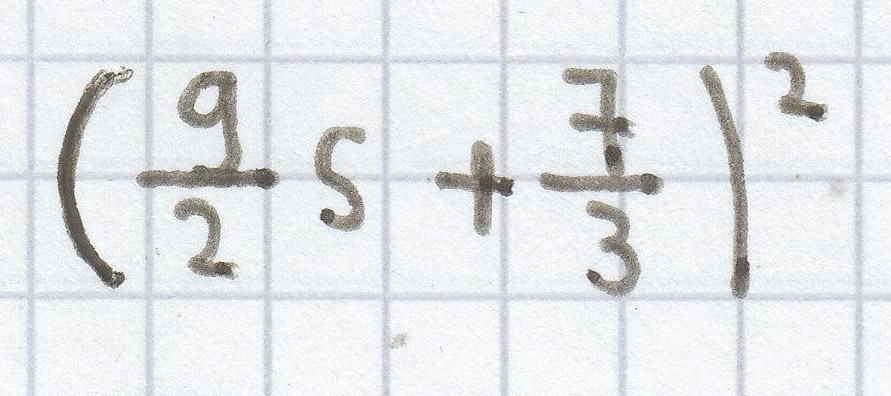
e)
(s + 3,1t)²
(d – 0,4e) (d + 0,4e)
(0,5a – b)²
f)
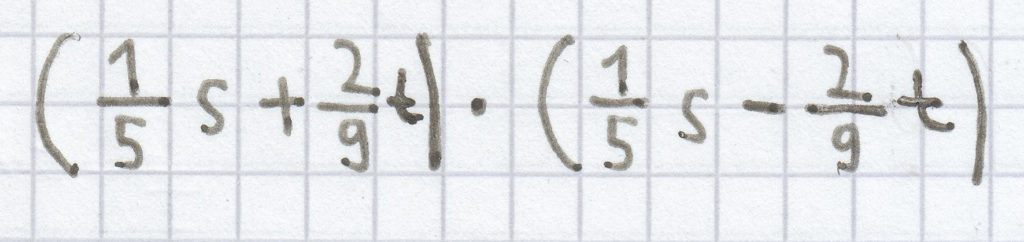
(3a + 9b) · (3a – 9b)
(2x + 3y) · (2x – 3y)
g)
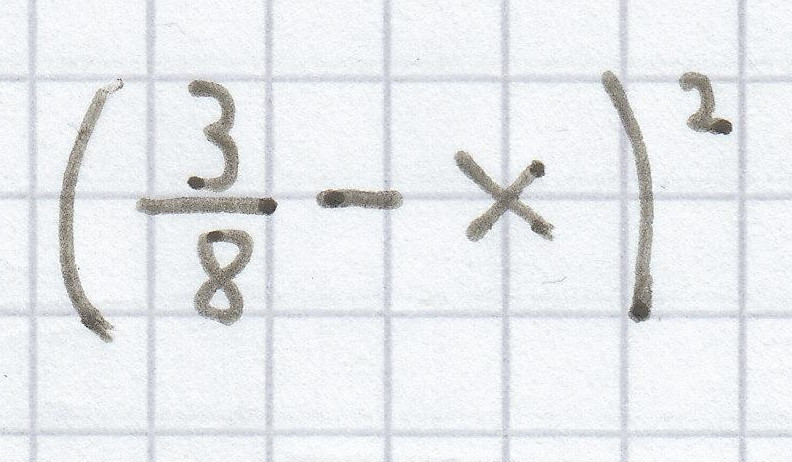
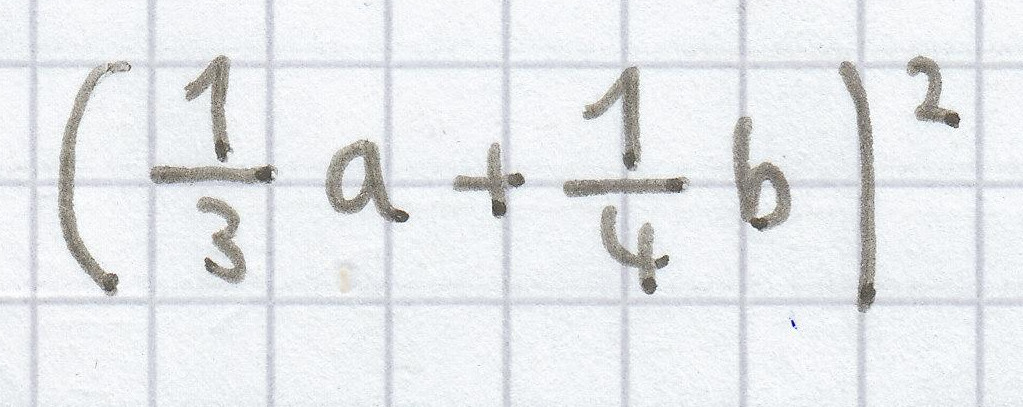

h)
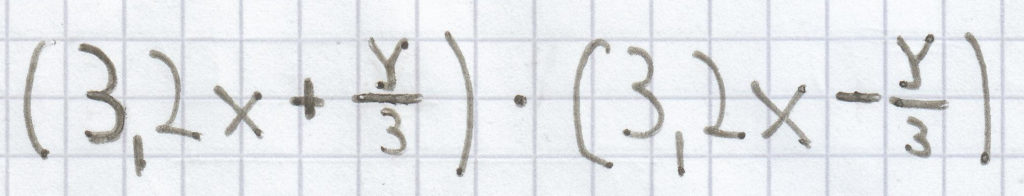

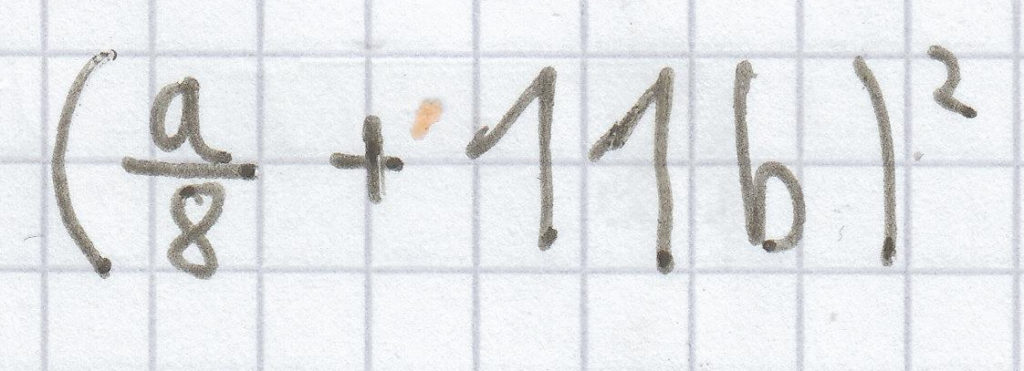
Lösungen zu dem Mathematik-Stoffgebiet: binomische Formeln
1. Mathematik-Nachhilfe-Aufgabe: Zuerst die binomische Formel erkennen, dann richtig auflösen.
a) (–8 + x)² = (x – 8)² = (x)² – 2 · x · 8 + (8)² = x² – 16x + 64
Durch Anwendung des Kommutativgesetzes/Vertauschungsgesetzes erhält man sofort die gewohnte unaufgelöste Form der 2. Binomischen Formel. Danach kann man das für die 2. Binomische Formel geltende Auflösungsschema benutzen, um diese in die augelöste Form zu bringen.
(a + (–3))² = (a – 3)² = (a)² – 2 · a · 3 + (3)² = a² – 6a + 9
Indem man die Plus-Klammer vor der „–3″ auflöst, erhält man sogleich die bekannte unaufgelöste Form der 2. Binomischen Formel. Darauf kann man das Auflösungsschema der 2. Binomischen Formel heranziehen.
(7 – (–b))² = (7 + b)² = (7) + 2 · 7 · b + (b)² = 49 + 14b + b² = b² + 14b + 49
Nach dem Auflösen der Minusklammer vor dem „–b“ erhält man sofort die unaufgelöste Form der 1. Binomischen Formel. Im Anschluss kann man mit dem für die 1. Binomische Formel geltenden Auflösungsschema die aufgelöste Form erzeugen.
(–8 – x)² = (–8 – x) (–8 – x) = (–1) · (8 + x) (8 + x) · (–1) = (8 + x) (8 + x) = (8 + x)² = (8)² + 2 · 8 · x + (x)² = 64 + 16x + x² = x² + 16x + 64
Nachdem man die Potenz „hoch 2″ aufgelöst hat, bei beiden Termen innerhalb der Klammer jeweils „–1″ ausgeklammert hat und die Potenz „hoch 2″ beim Term wieder erzeugt hat, erhält man schließlich die unaufgelöste Form der 1. Binomischen Formel. Darauf kann man mit dem gewohnten Auflösungsschema der 1. Binomischen Formel diese in die aufgelöste Form bringen.
b) (a + (–b))² = (a – b)² = (a)² – 2 · a · b + (b)² = a² – 2ab + b²
Nachdem man die Plus-Klammer vor dem „–b“ aufgelöst hat, erhält man sogleich die unaufgelöste Form der 2. Binomischen Formel. Mit dem bekannten Auflösungsschema der 2. Binomischen Formel kann man diese dann in die aufgelöste Form bringen.
(–x – y)² = (–x – y) (–x – y) = (–1) · (x + y) (x + y) · (–1) = (x + y) (x + y) = (x + y)² = (x)² + 2 · x · y + (y)² = x² + 2xy + y²
Zunächst löst man die Potenz „hoch 2″ auf. Danach klammert man bei beiden Klammern den Faktor „–1″ aus. Darauf erzeugt man wieder die Potenz „hoch 2″. Dann zeigt sich eindeutig die unaufgelöste Form der 1. Binomischen Formel. Mit dem gewohnten Auflösungsschema der 1. Binomischen Formel kann man diese darauf in die unaufgelöste Form bringen.
(– y + x)² = (x – y)² = (x)² – 2 · x · y + (y)² = x² – 2xy + y²
Nach Anwendung des Kommutativgesetzes/Vertauschungsgesetzes erhält man sofort die unaufgelöste Form der 2. Binomischen Formel. Mittels des bekannten Auflösungsschemas der 2. Binomischen Formel kann man diese dann in die aufgelöste Form bringen.
(–a + (–b))² = (–a – b)² = (–a – b) (–a – b) = (–1) · (a + b) (a + b) · (–1) = (a + b) (a + b) = (a + b)² = (a)² + 2 · a · b + (b)² = a² + 2ab + b²
Nach Auflösung der Plus-Klammer, Auflösung der Potenz „hoch 2″, dem doppelten Ausklammern des Faktors „–1″ und dem erneuten Erzeugen der Potenz „hoch 2″ erhält man innerhalb des Terms die 1. Binomische Formel in der unaufgelösten Form. Mit dem gewohnten Auflösungschema der 1. Binomischen Formel kann man diese dann in die aufgelöste Form umwandeln.

c) (3a + (–5b))² = (3a – 5b)² = (3a)² – 2 · 3a · 5b + (5b)² = 9a² – 30ab + 25b²
Nach Auflösung der Plusklammer zeigt sich sofort die unaufgelöste Form der 2. Binomischen Formel. Mittels des bekannten Auflösungsschemas der 2. Binomischen Formel kann man diese sodann in die unaufgelöste Form bringen.
(–7a + b)² = (b – 7a)² = (b)² – 2 · b · 7a + (7a)² = b² – 14ba + 49a² = 49a² – 14ab + b²
Nach Anwendung des Kommutativgesetzes/Vertauschungsgesetzes erhält man sofort die 2. Binomische Formel in der unaufgelösten Form. Durch Heranziehen des gewohnten Auflösungsschemas der 2. Binomischen Formel kann man diese dann in die aufgelöste Form bringen.
(–9x – 3y)² = (–9x – 3y) (–9x – 3y) = (–1) · (9x + 3y) (9x + 3y) · (–1) = (9x + 3y)² = (9x)² + 2 · 9x · 3y + (3y)² = 81x² + 54xy + 9y²
Zuerst löst man hier die Potenz „hoch 2″ auf. Darauf klammert man bei jeder Klammer den Faktor „–1″ aus. Danach erzeugt man wieder die Potenz „hoch 2″ beim Term. Nun sieht man sofort, dass es sich hier um die 1. Binomische Formel in der unaufgelösten Form handelt. Mittels des bekannten Auflösungsschemas der 1. Binomischen Formel kann man diese dann in die unaufgelöste Form bringen.
(–2a – (–5b))² = (–2a + 5b)² = (5b – 2a)² = (5b)² – 2 · 5b · 2a + (2a)² = 25b² – 20ba + 4a² = 4a² – 20ab + 25b²
Nach Auflösung der Minusklammer und Anwendung des Kommutativgesetzes/Vertauschungsgesetzes erhält man die unaufgelöste Form der 2. Binomischen Formel. Danach kann man mithilfe des für die 2. Binomischen Formel geltenden Auflösungsschemas diese in die unaufgelöste Form bringen.
d) (4r + 9s) · (–4r + 9s) = (9s + 4r) · (9s – 4r) = (9s)² – (4r)² = 81s² – 16r²
Wendet man jeweils bei den Einzeltermen innerhalb der beiden Klammern das Kommutativgesetz/Vertauschungsgesetz an, so erhält man die 3. Binomische Formel in der unaufgelösten Form. Diese kann man mit dem bekannten Auflösungsschema der 3. Binomischen Formel auflösen.
(–8x + 5y)² = (5y – 8x)² = (5y)² – 2 · 5y · 8x + (8x)² = 25y² – 80yx + 64x² = 64x² – 80xy + 25y²
Nach Anwendung des Kommutativgesetzes/Vertauschungsgesetzes erhält man sofort die 2. Binomische Formel in der unaufgelösten Form. Darauf kann man mittels des Auflösungsschemas der 2. Binomischen Formel diese in die aufgelöste Form umwandeln.
(2a – 6b) · (2a + 6b) = (2a + 6b) · (2a – 6b) = (2a)² – (6b)² = 4a² – 36b²
Nach Anwendung des Kommutativgesetzes/Vertauschungsgesetzes bei den beiden Faktoren des Produktes zeigt sich sofort die 3. Binomische Formel in der unaufgelösten Form. Mithilfe des gewohnten Auflösungsschemas der 3. Binomischen Formel kann man diese dann in die aufgelöste Form bringen.
(–x + 6y) · (–x – 6y) = (–1) · (x – 6y) · (x + 6y) · (–1) = (x + 6y) (x – 6y) = (x)² – (6y)² = x² – 36y²
Nach Ausklammern von jeweils dem Fakor „–1″ bei beiden Klammern und Anwendung des Kommutativgesetzes/Vertauschungsgesetzes bei den Faktoren des Produktes erhält man die 3. Binomische Formel in der unaufgelösten Form. Darauf kann man diese mithilfe des gewohnten Auflösungsschemas der 3. Binomischen Formel in die aufgelöste Form bringen.
2. Mathe-Nachhilfe-Aufgabe: Schon ein Experte im Auflösen von binomischen Formeln?
a)
(7a + 9)² = (7a)² + 2 · 7a · 9 + (9)² = 49a² + 126a + 81
(9s + 3t)² = (9s)² + 2 · 9s · 3t + (3t)² = 81s² + 54st + 9t²
(0,8u – 6)² = (0,8u)² – 2 · 0,8u · 6 + (6)² = 0,64u² – 9,6u + 36
b)
(12x + 8y)² = (12x)² + 2 · 12x · 8y + (8y)² = 144x² + 192xy + 64y²
(7k – 3)² = (7k)² – 2 · 7k · 3 + (3)² = 49k² – 42k + 9
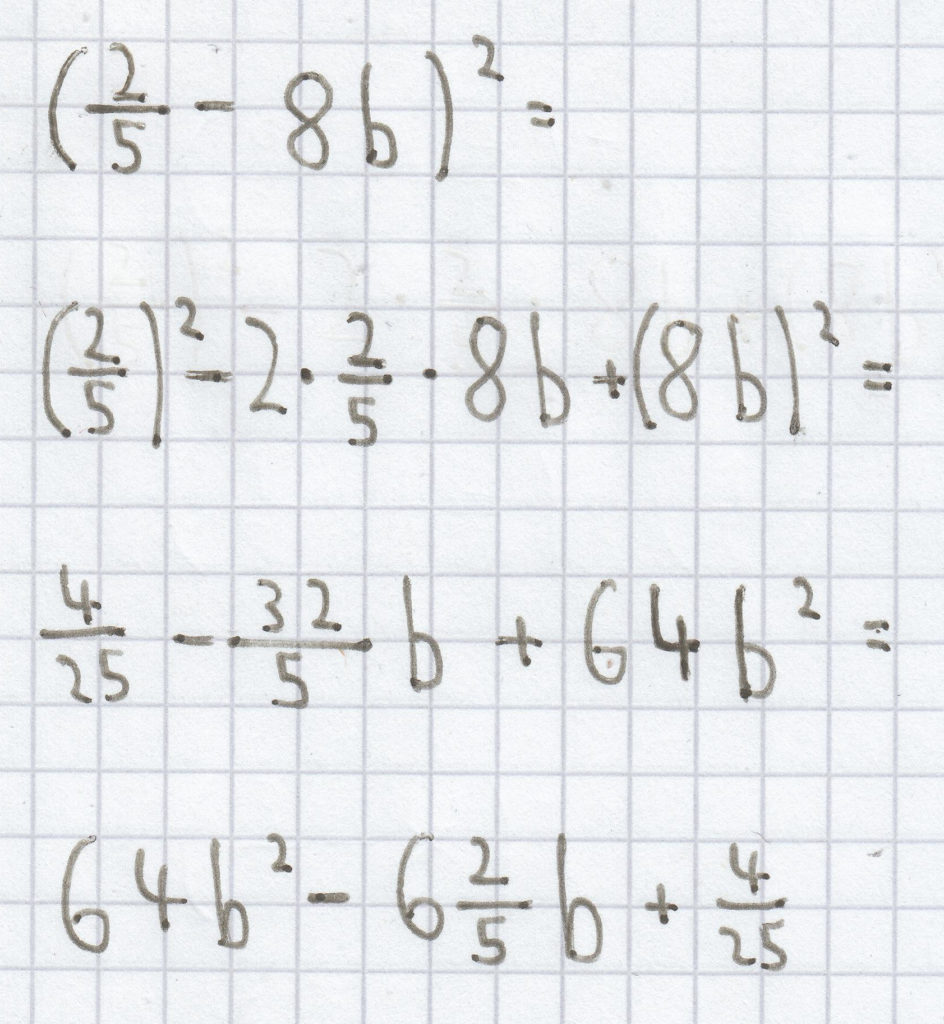
c)
(3,6 + a)² = (3,6)² + 2 · 3,6 · a + (a)² = 12,96 + 7,2a + a² = a² + 7,2a + 12,96
(x + 7,8) (x – 7,8) = (x)² – (7,8)² = x² – 60,84
(y – 1,5)² = (y)² – 2 · y · 1,5 + (1,5)² = y² – 3y + 2,25
d)
(7a – 15)² = (7a)² – 2 · 7a · 15 + (15)² = 49a² – 210a + 225
(14x – 20)² = (14x)² – 2 · 14x · 20 + (20)² = 196x² – 560x + 400
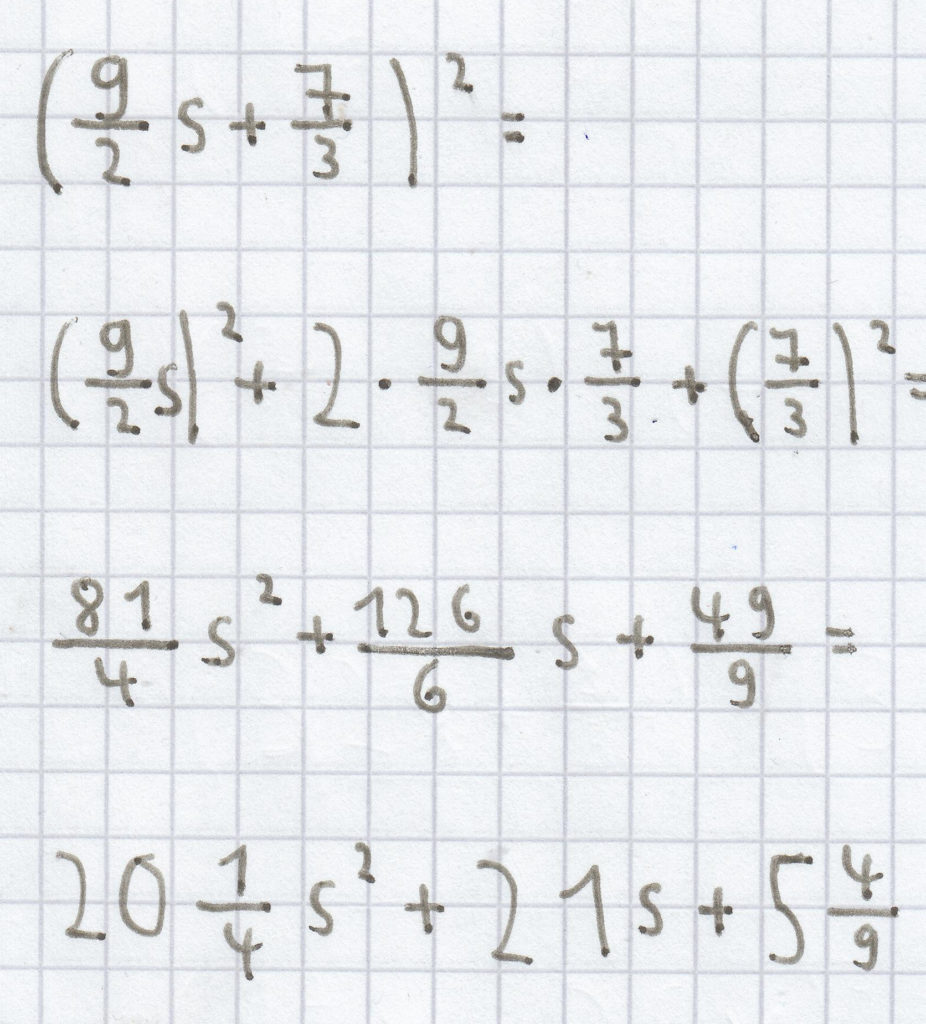
e)
(s + 3,1t)² = (s)² + 2 · s · 3,1t + (3,1t)² = s² + 6,2st + 9,61t²
(d – 0,4e) (d + 0,4e) = (d)² – (0,4e)² = d² – 0,16e²
(0,5a – b)² = (0,5a)² – 2 · 0,5a · b + (b)² = 0,25a² – ab + b²
f)
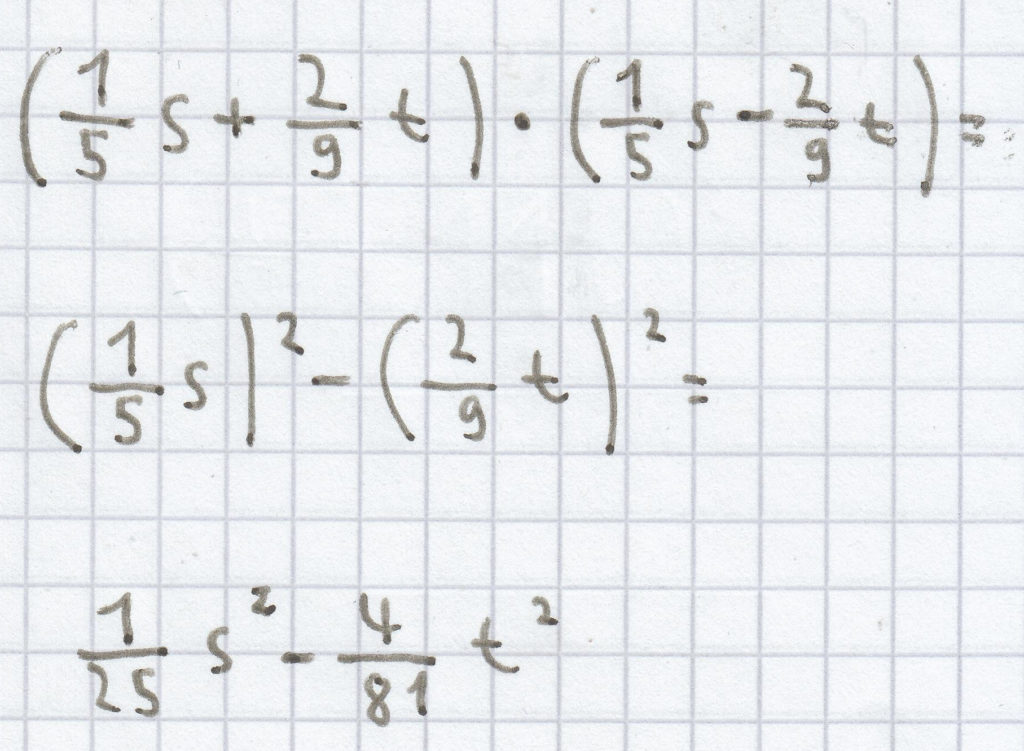
(3a + 9b) · (3a – 9b) = (3a)² – (9b)² = 9a² – 81b²
(2x + 3y) · (2x – 3y) = (2x)² – (3y)² = 4x² – 9y²
g)
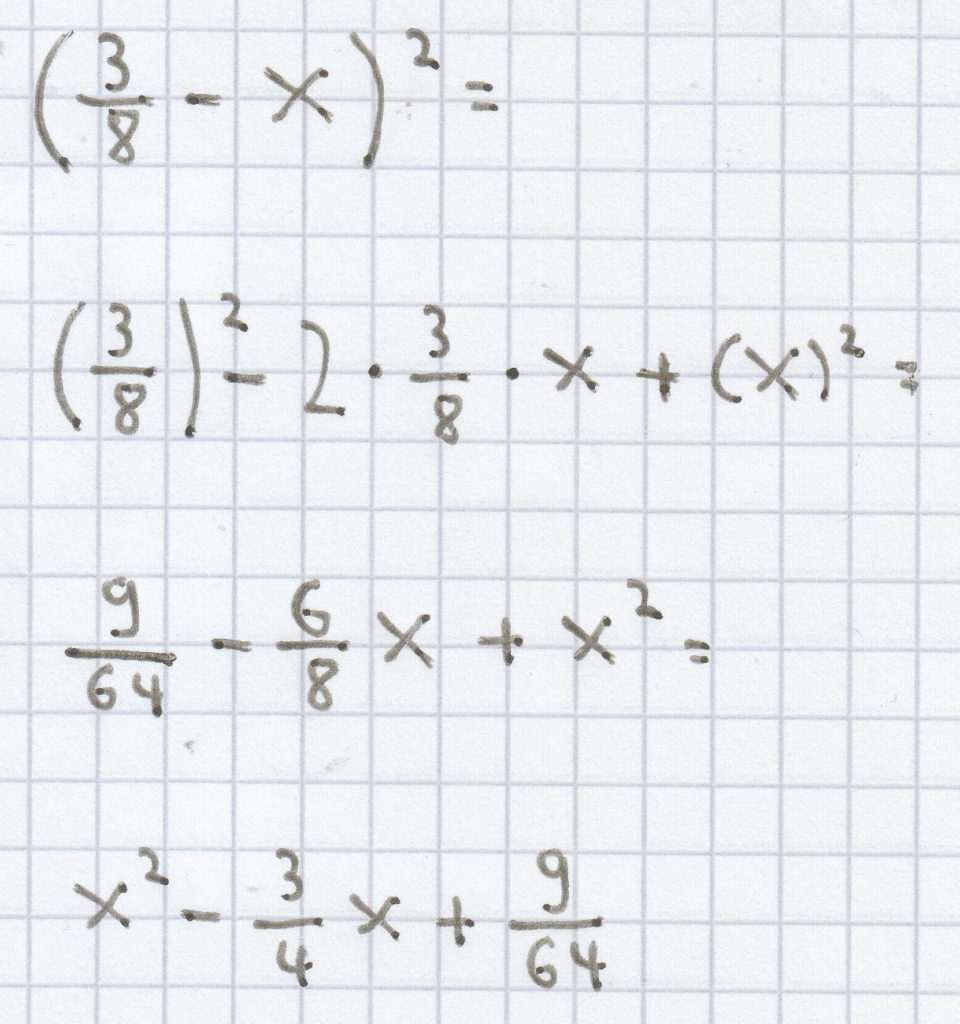
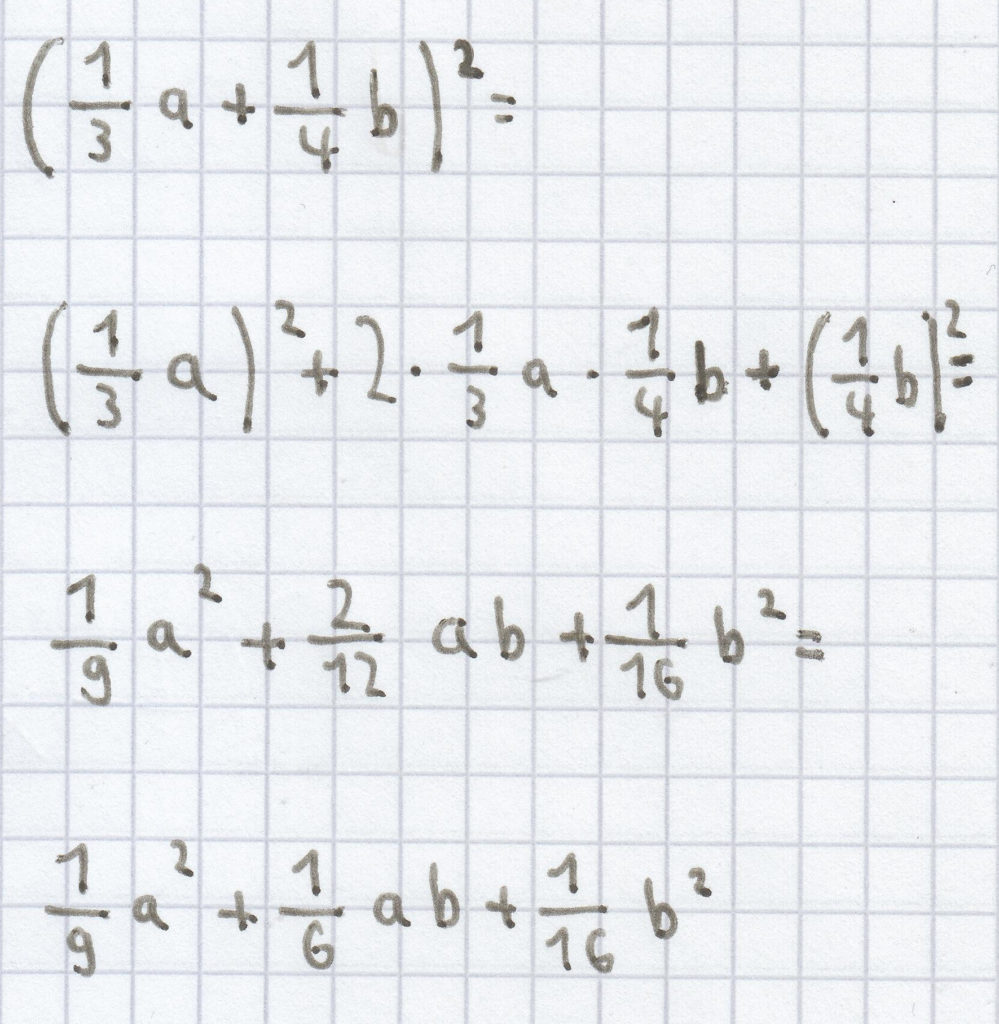
h)