
Die Kultband ABBA konnte bereits ein Lied davon singen. Denn in MONEY MONEY MONEY aus dem Jahre 1976 thematisiert ABBA auf sehr melodische Art und Weise die Sonnen- und Schattenseiten von Geld. Je nachdem, ob man Geld hat, so die Lyrics des Songs, „must money money money be funny in the rich man’s world“ oder „sad“, wenn man hierfür „work all night, all day to pay the bills“. Aus dem Song kann man daher unstrittig heraushören, dass Geld etwas Anziehendes und Abstoßendes zugleich ist. Je älter man wird, desto mehr wird man das noch feststellen, da man immer mehr sehen wird, dass es in der Welt viel an Ungerechtigkeit gibt. Und der Hauptgrund hierfür liegt in der ungerechten Verteilung von Geld. Aber nicht nur ABBA kann hiervon ein Lied singen, sondern Abermillionen andere Menschen weltweit!

In der Schule im Fach Mathematik spielt Geld beziehungsweise der Geldwert bei dem Stoffgebiet Größen auch bereits eine Rolle, bei dem späteren Stoffgebiet Zinsrechnen aber eine noch viel größere. Geld hat nämlich bekanntlich die Eigenschaft, dass man es auf unterschiedliche Weise vermehren kann. Ein gängiger Weg ist hierbei über eine Geldanlage, da man hierfür über einen bestimmten Zeitraum Zinsen bekommt. Die Zinsrechnung kreist demzufolge um die Berechnung dieser Zinsen/Z, den Zinssatz/p %, der überhaupt das Mehr an Geld ermöglicht, sowie das Kapital/K, das man bei einer Bank gewinnbringend anlegt.
Beim Zinsrechnen sind zunächst folgende drei Mathe-Formeln wichtig:
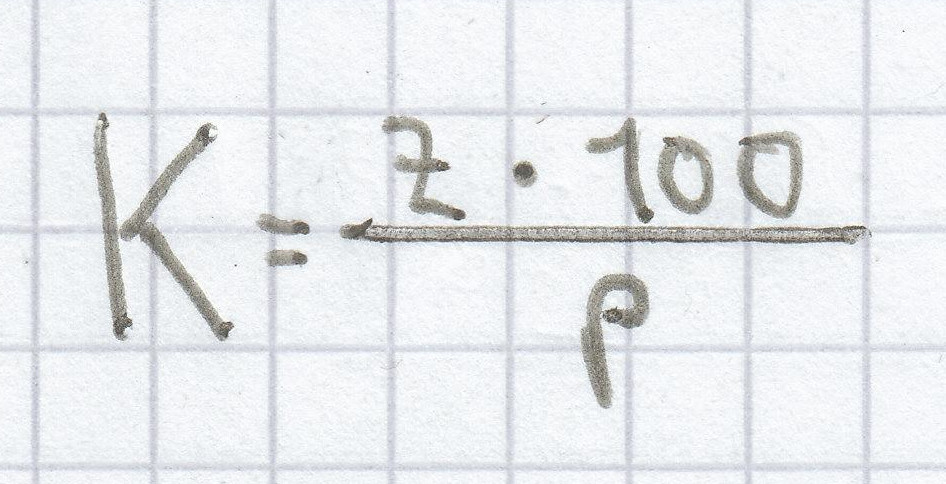
;
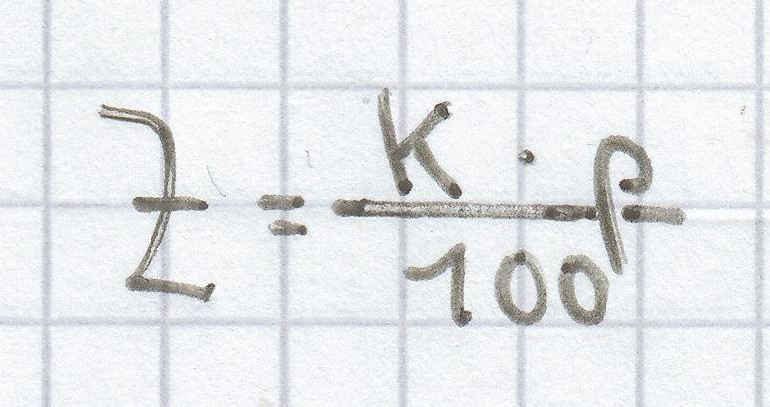
;
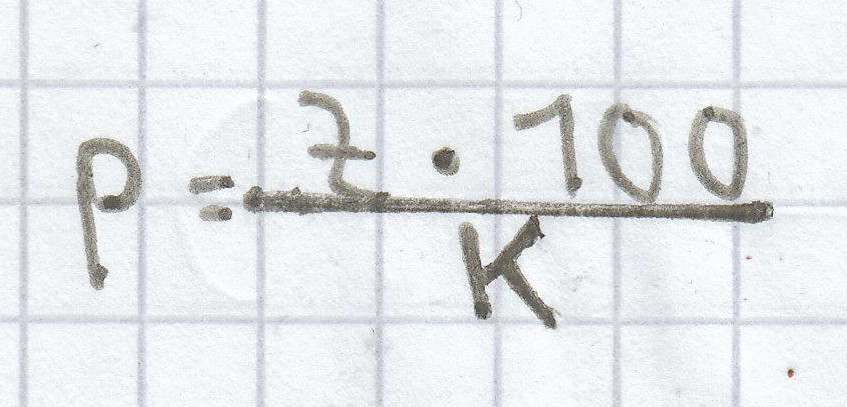
Aufgaben zum Mathematik-Stoffgebiet Zinsrechnen
1. Mathe-Nachhilfe-Aufgabe: Rechnungen rund um Jahreszinsen.
a) Ein Kapital von 5000 € wird mit einem Zinssatz von 2,5 % gewinnbringend angelegt. Wie hoch sind die Jahreszinsen?
b) Ein Kapital erwirtschaftet über ein Jahr 40 € an Zinsen bei einem Zinssatz von 2 %. Wie hoch ist das angelegte Kapital?
c) Ein Kapital von 8000 € wird nach einem Jahr 100 € an Zinsen ab. Wie hoch ist der Zinssatz?
2. Mathe-Nachhilfe-Aufgabe: Ermittlung des Zinssatzes.
Herr Schröder hat einen Geldbetrag von 25000 Euro bei einer Bank angelegt und hierdurch 500 Euro an Zinsen erhalten. Wie hoch ist der Zinssatz gewesen?
3. Mathematik-Nachhilfe-Aufgabe: Berechne die Zinsen.
Frau König will sich ein neues Auto kaufen. Hierfür fehlen ihr aber noch 6000 €. Das Geld leiht sich sich für einen Zinssatz von 8 % von einer Bank. Wie hoch sind die anfallenden Jahreszinsen?
4. Mathematik-Nachhilfe-Aufgabe: Berechne die Höhe eines angewachsenen Kapitals.
Auf einer Bank werden 800 Euro [1200 Euro, 2500 Euro] zu einem Zinssatz von 2,5 Prozent verzinst. Wie hoch ist das Kapital nach einem Jahr angewachsen? Berechne dies auf zwei unterschiedliche Arten!
5. Mathe-Nachhilfe-Aufgabe: Ermittle den Zinssatz.
Ein Kapital von 6300 Euro wächst über ein Jahr auf 6500 Euro an. Wie hoch war der Zinssatz?
6. Mathematik-Nachhilfe-Aufgabe: Berechne das Kapital und den Kapitalzuwachs.
Ein Kapital wirft bei einem Zinssatz von 3 % in einem Jahr 45 € [81 €; 234 €] an Zinsen ab.
a) Wie hoch ist das angelegte Kapital?
b) Wie hoch ist das Kapital nach einem Jahr?

Lösungen zum Mathe-Stoffgebiet Zinsrechnung
1. Mathematik-Nachhilfe-Aufgabe: Was man bei Jahreszinsen alles für Berechnungen machen kann.
a) Berechne die Jahreszinsen bei einem Anlagebetrag von 5000 € und einem Zinssatz von 2,5 %.
Hierfür muss man diese Formel heranziehen:
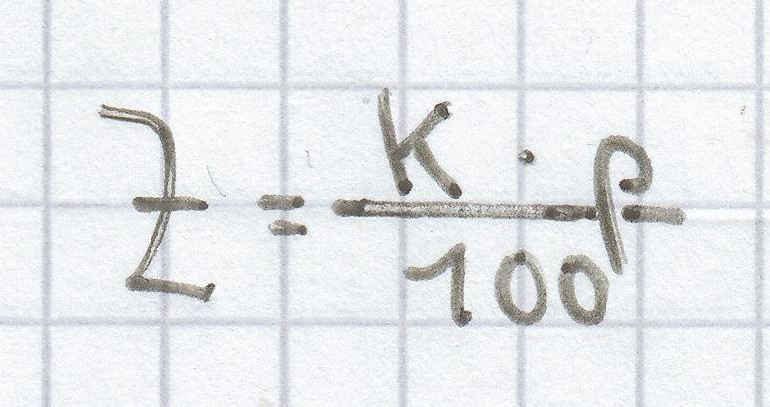
, eingesetzt ergibt sich:
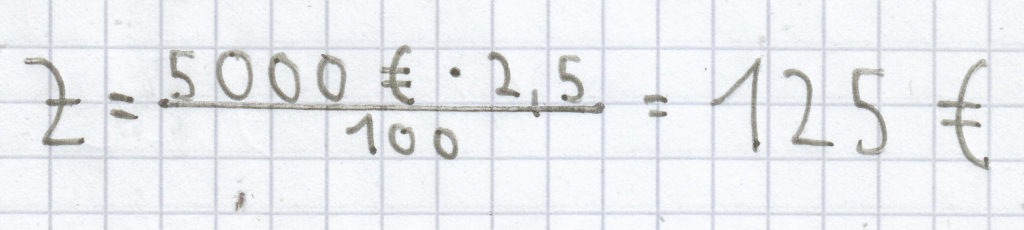
.
Nach einem Jahr fallen 125 € an Zinsen an.
b) Wie hoch ist der angelegte Betrag, wenn bei einem Zinssatz von 2 % nach einem Jahr 40 € an Zinsen anfallen?
Zur Berechnung des Kapitals muss man folgende Formel benutzen:
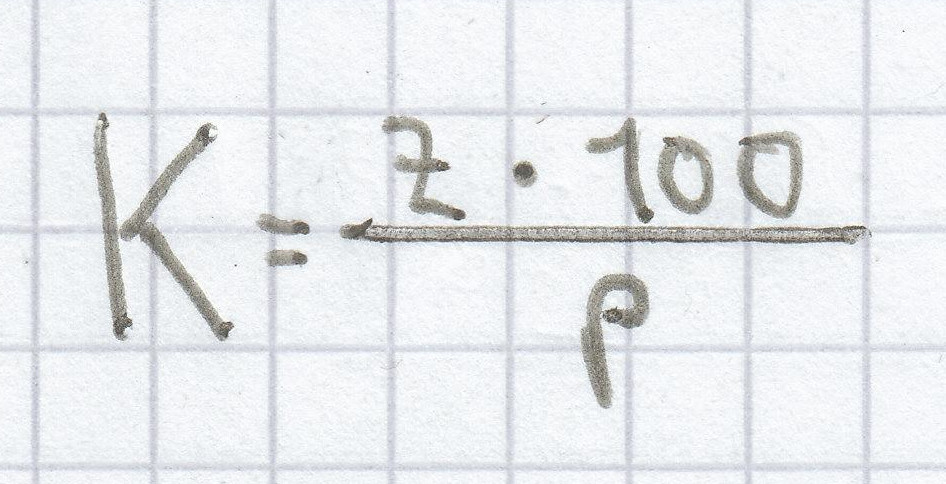
, eingesetzt ergibt sich:
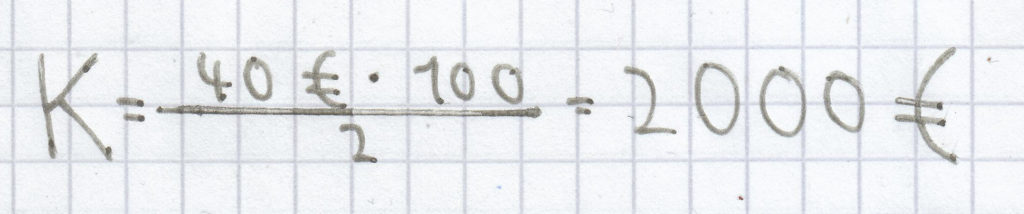
.
Es wurden 2000 € angelegt.
c) Wie hoch ist der Zinssatz bei einem Anlagebetrag von 8000 €, der nach einem Jahr 100 € an Zinsen abwirft?
Diese Formel muss hier herangezogen werden:
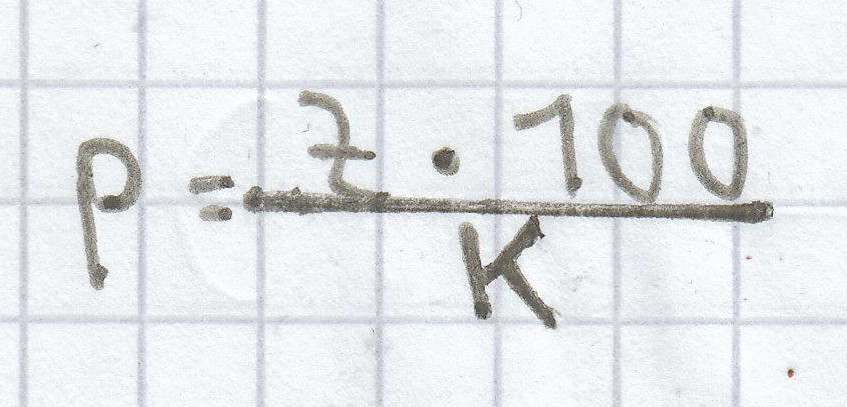
, eingesetzt ergibt sich:
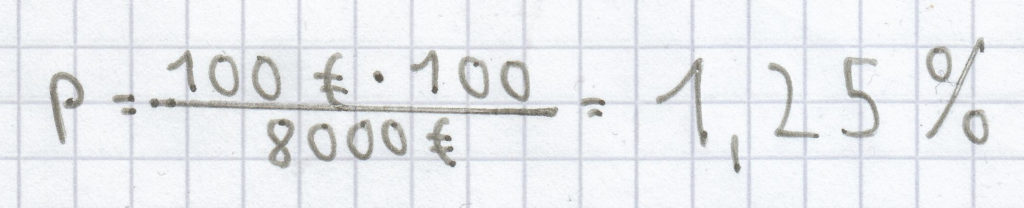
.
Der Zinssatz beträgt 1,25 %.
2. Mathe-Nachhilfe-Aufgabe: Berechne die Höhe des Zinssatzes.
Herr Schröder erhielt für einen angelegten Geldbetrag von 25000 Euro 500 Euro an Zinsen. Wie hoch ist der Zinssatz gewesen?
Zur Berechnung des Zinssatzes muss diese Formel herangezogen werden:
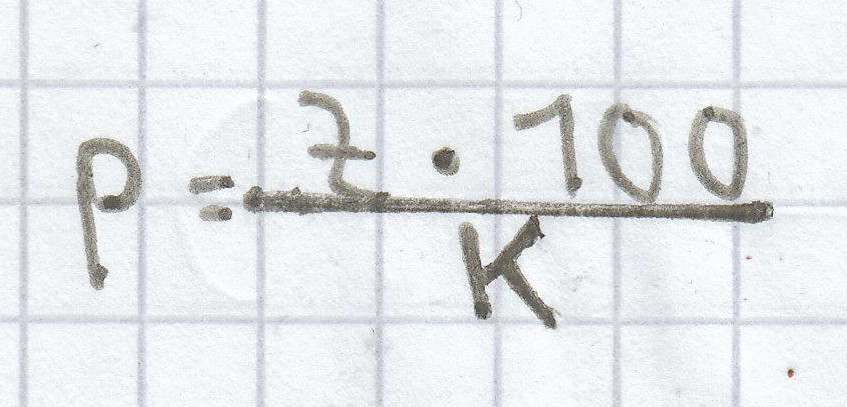
, eingesetzt ergibt sich:
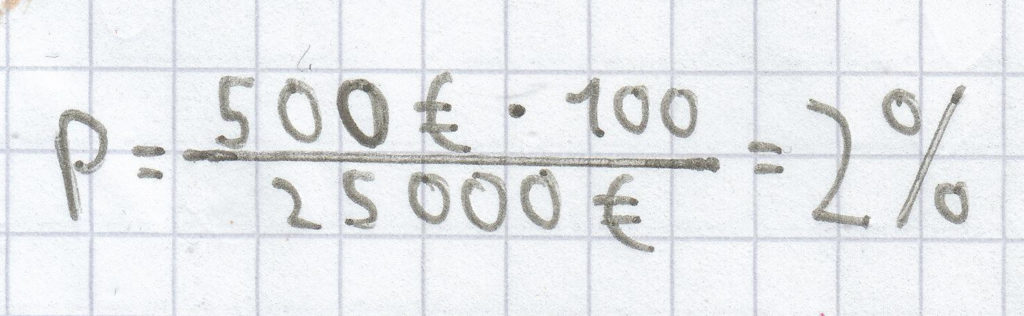
Der Zinssatz betrug 2 %.
3. Mathematik-Nachhilfe-Aufgabe: Berechne die Höhe der anfallenden Zinsen.
Frau König leiht sich von einer Bank 6000 € zu einem Zinssatz von 8 %.
Mit folgender Formel kann man die Zinsen berechnen:
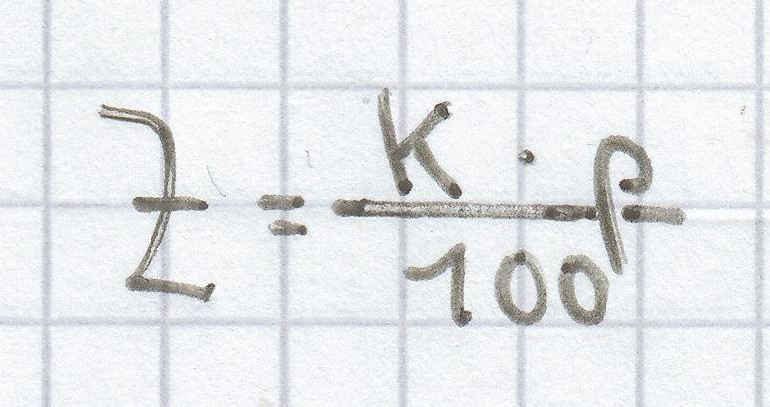
, eingesetzt ergibt sich:

.
Frau König muss für das geliehene Geld 480 € an Zinsen bezahlen.
4. Mathematik-Nachhilfe-Aufgabe: Wie hoch ist ein angelegtes Kapital jeweils nach einem Jahr angewachsen? Berechne den Zuwachs auf zwei verschieden Arten.
Das Kapital ist hierbei 800 € [1200 €; 2500 €]. Der Zinssatz beträgt 2,5 %.
Die Formel zur Berechnung der Zinsen ist eine Möglichkeit, um den Zuwachs zu ermitteln. Diese ist folgende:
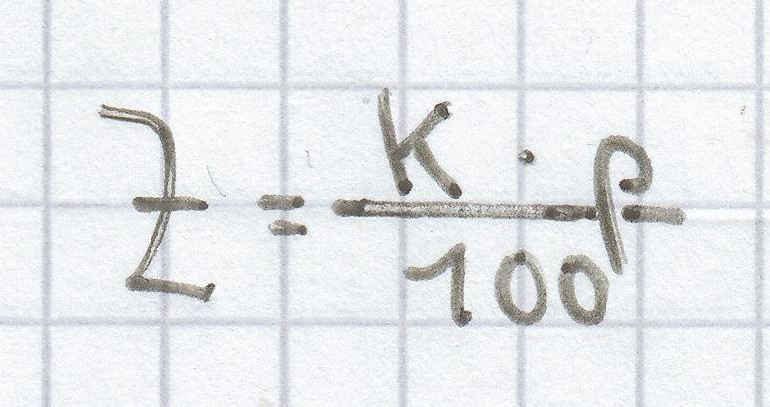
, eingesetzt ergibt sich:
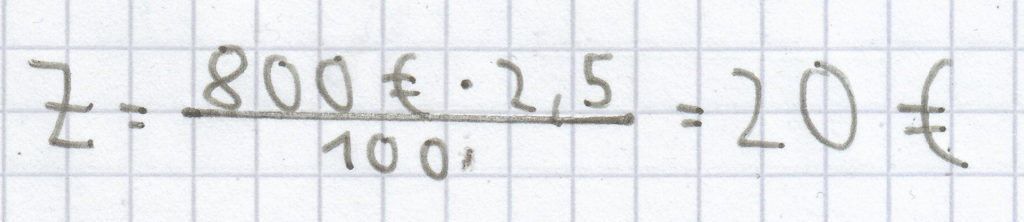
.
Die Zinsen nach einem Jahr betragen 20 €. Das Kapital ist somit auf 820 € (800 € + 20 €) angewachsen.
Direkt die Zunahme kann man über den Wachstumsfaktor berechnen. Diese berechnet sich wie folgt:
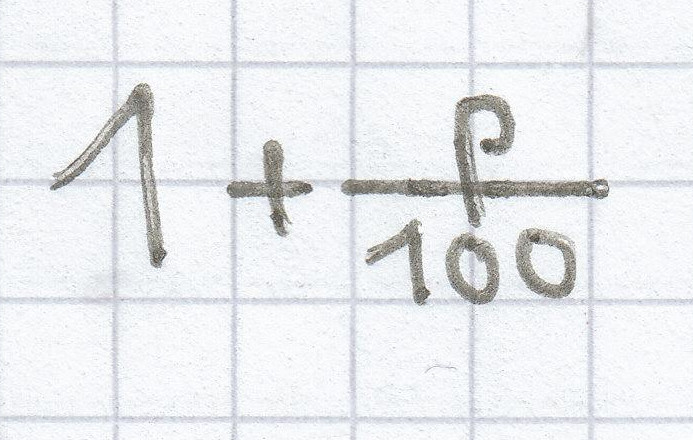
, bezogen auf die Aufgabe ergibt sich:
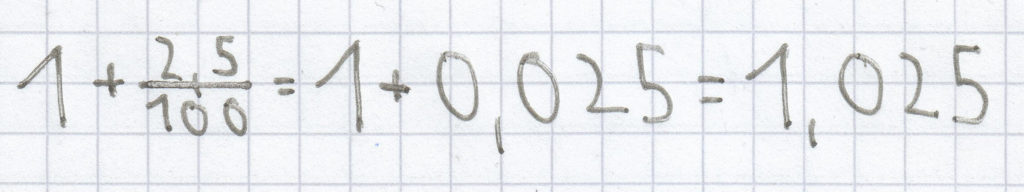
.
Das Wachstum berechnet sich nun, indem man den Grundwert mit dem Wachstumsfaktor multipliziert: Wachstum = 800 · 1,025 = 820.
Nach einem Jahr sind die 800 € auf 820 € angewachsen.
Bei 1200 €:
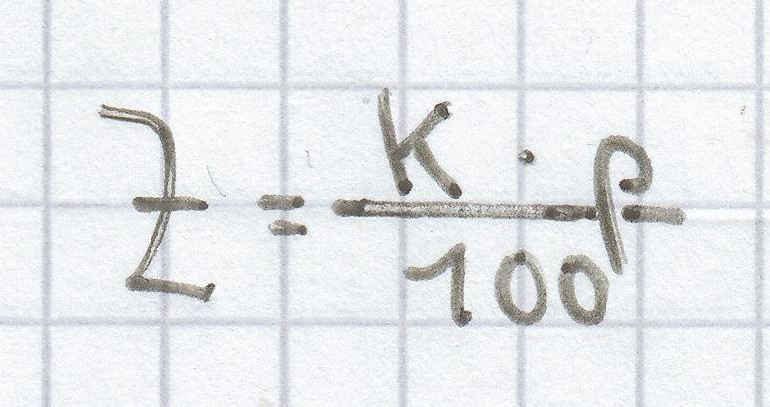
, eingesetzt ergibt sich:
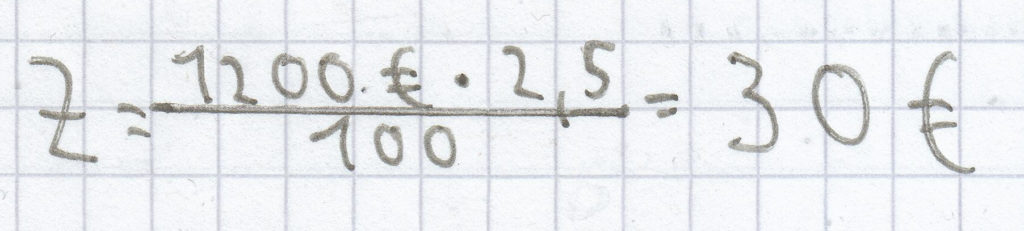
.
Nach einem Jahr ist das Geld hier auf 1230 € (1200 € + 30 €) angewachsen.
Wachstum = 1200 · 1,025 = 1230
Bei 1200 € ist das Kapital nach einem Jahr auf 1230 € angewachsen.
Bei 2500 €:
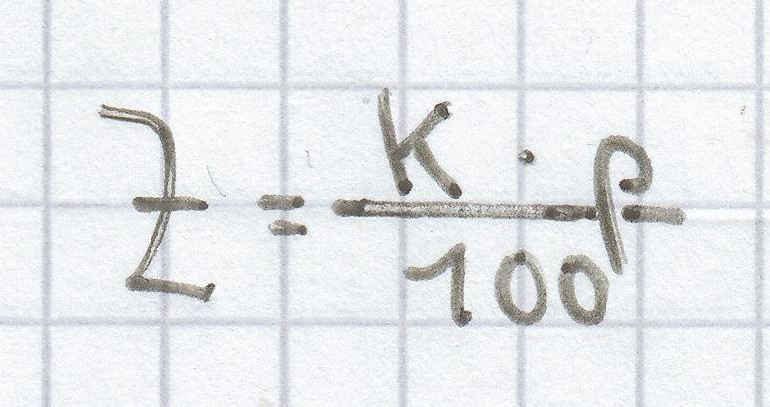
, eingesetzt ergibt sich:
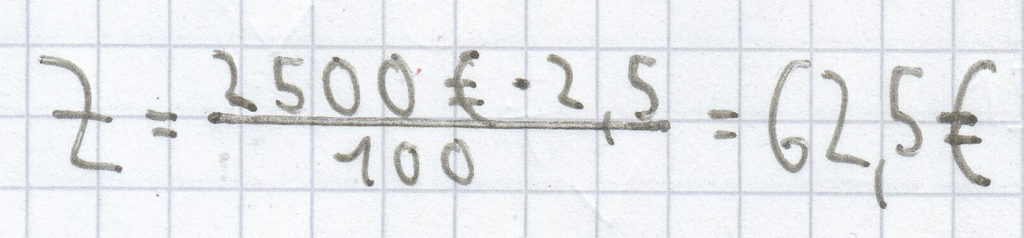
.
Hier ist das Kapital nach einem Jahr auf 2562,50 € ( 2500 € + 62,5) angewachsen.
Wachstum = 2500 · 1,025 = 2562,50
Nach einem Jahr ist das angelegte Kapital auf 2562,50 € angewachsen.
5. Mathematik-Nachhilfe-Aufgabe: Wie hoch ist der Zinssatz?
Ein angelegtes Kapital in Höhe von 6300 € ist nach einem Jahr auf 6500 Euro angewachsen.
Die Zinsen betragen hier 200 € (6500 € – 6300 €). Nun kann man die Formel zur Berechnung des Zinssatzes heranziehen.
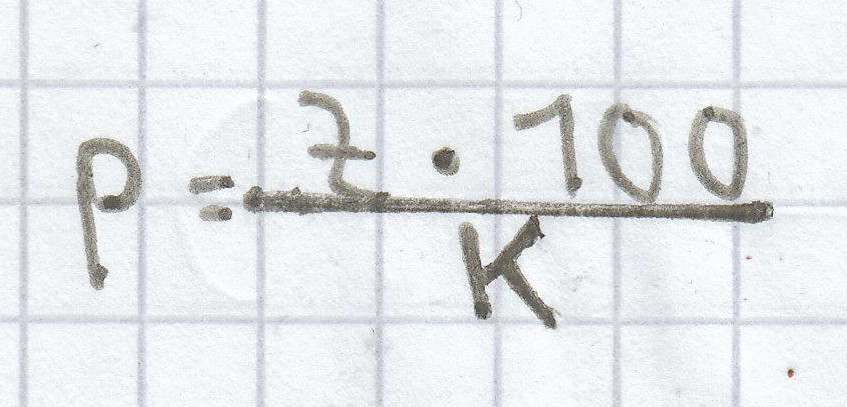
, eingesetzt ergibt sich:
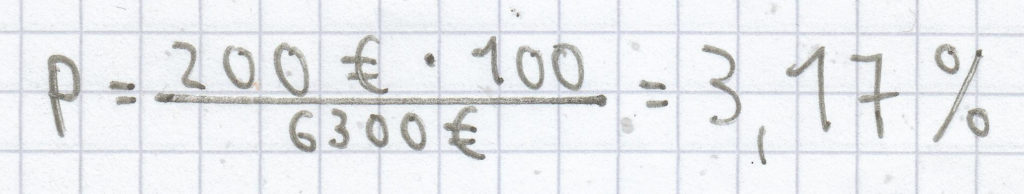
(gerundet auf zwei Nachkommastellen).
Der Zinssatz betrug 3,17 %.
6. Mathe-Nachhilfe-Aufgabe: Berechne das Kapital und den Kapitalzuwachs.
Der Zinssatz beträgt 3 %. Nach einem Jahr fallen 45 € [81 €; 234 €] an Zinsen an.
Die Formel zur Berechnung des Kapitals ist folgende:
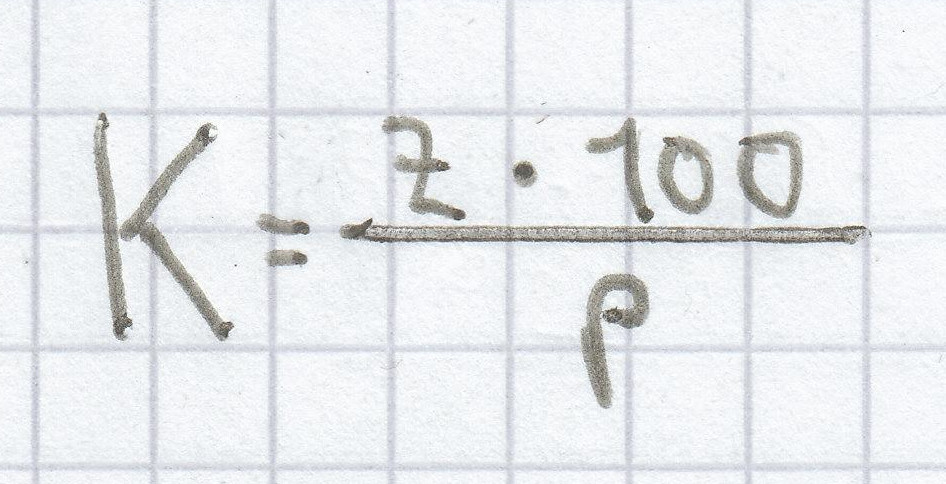
, eingesetzt ergibt sich:
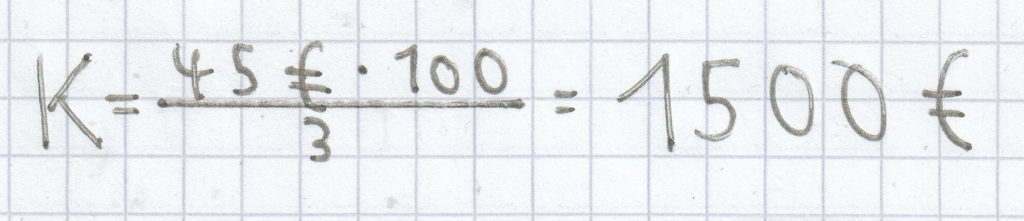
.
Die 45 € an Zinsen basieren auf einem Anlagebetrag von 1500 €. Das Kapitalt ist somit nach einem Jahr auf 1545 € (1500 € + 45 €) angewachsen.
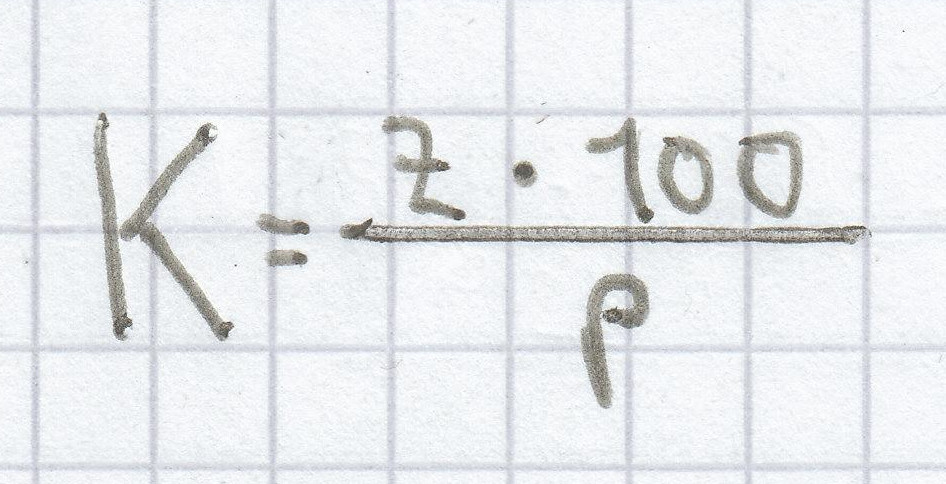
, eingesetzt ergibt sich:
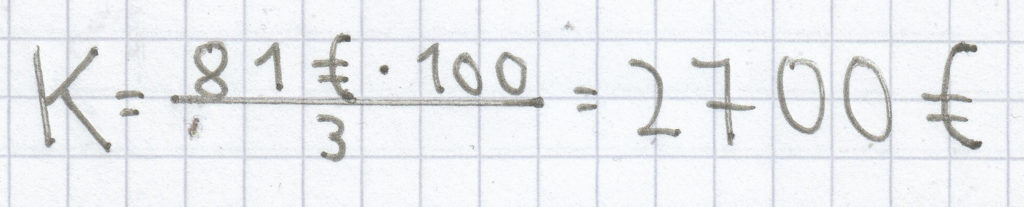
.
Bei 81 € an anfallenden Zinsen ergibt sich ein angelegtes Kapital von 2700 €. Das Kapital ist daher auf 2781 € (2700 € + 81) hin angewachsen.
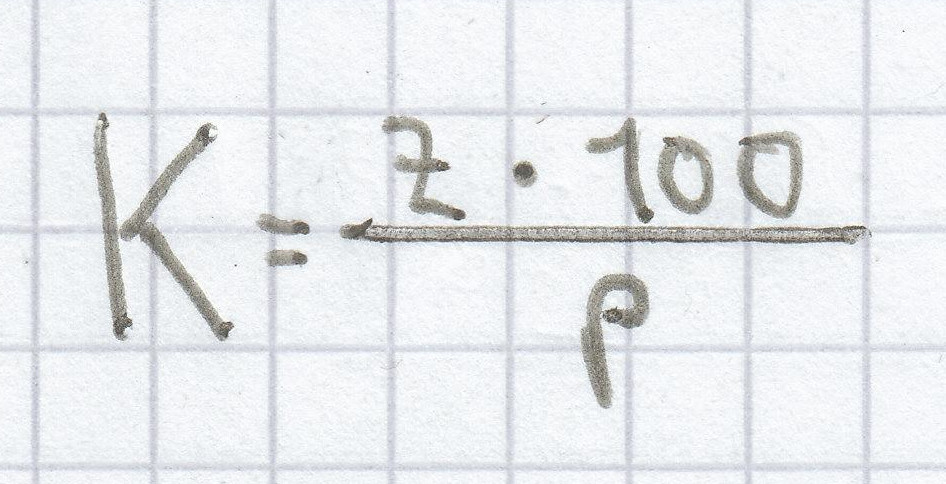
, eingesetzt ergibt sich:
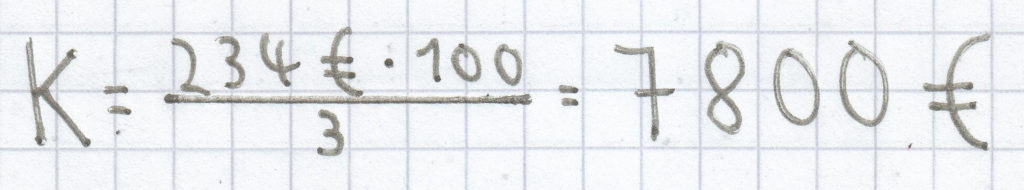
.
Bei 234 € an Jahreszinsen ergibt sich ein Kapital in Höhe von 7800 €. Das Kapital ist somit auf 8034 € hin (7800 € + 234 €) angewachsen.