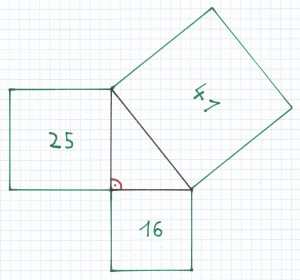
Die Mathematik ist etwas sehr altes. Bereits in der Antike beschäftigten sich Menschen damit. Als Schülerin und Schüler weiß man das natürlich oft nicht. Warum auch? Mathe-Gesetze „fühlen“ sich eh zeitlos an! Daher ist beispielsweise der Satz des Pythagoras auch noch in 500 Millionen Jahren gültig – und darüber hinaus. Dennoch müssen Menschen erst auf solch eine Mathe-Gesetzmäßigkeit stoßen, was bei dem Satz des Pythagoras schon superlange her ist. Denn bereits im 6. Jahrhundert vor Christus stieß angeblich Pythagoras auf die nach ihm benannte sehr berühmte Gesetzmäßigkeit. Heute weiß man aber, dass auch schon vor ihm Babylonier und Ägypter diese Gesetzmäßigkeit kannten. In der Schule beim Satz des Pythagoras bekommt man daher spätestens einen Begriff davon, wie alt die Mathematik doch ist…
Aufgaben zum Mathe-Stoffgebiet Satz des Pythagoras
1. Mathematik-Nachhilfe-Aufgabe: Ermittle für folgende Dreiecke jeweils drei verschiedene Gesetzmäßigkeiten, um aus zwei Seiten die dritte Seite zu berechnen.
a) γ = 90°
b) α = 90°
c) β = 90°
2. Mathe-Nachhilfe-Aufgabe: Ermittle die Höhe einer angelehnten Leiter.
Eine Leiter mit der Länge 4,20 m lehnt an einer Mauer. Von der Mauer ist ihr Fußende 2,20 m entfernt. Wie Hoch ist die Leiter an der Mauer angelehnt? Mache zuerst eine Skizze.
3. Mathematik-Nachhilfe-Aufgabe: Ziehe den Satz des Pythagoras heran, um folgende Strecken zu bilden:
a) [latexpage] $\sqrt{\ {10}$
b) [latexpage] $\sqrt{\ {20}$
c) [latexpage] $\sqrt{\ {2}$
4. Mathe-Nachhilfe-Aufgabe: Bilde mithilfe des Satz des Pythagoras ein Quadrat, das folgenden Flächeninhalt vorweist.
a) A = 2 cm²
b) A = 27 cm²
c) A = 13 cm²
d) A = 12 cm²
e) A = 41 cm²
Lösungen zum Mathematik-Stoffgebiet Satz des Pythagoras
1. Mathe-Nachhilfe-Aufgabe: Bestimme für alle rechtwinkligen Dreieck drei verschiedene Gesetzmäßigkeiten, damit mithilfe von zwei Seiten jeweils die dritte Seite ermittelt werden kann.
a) γ = 90°
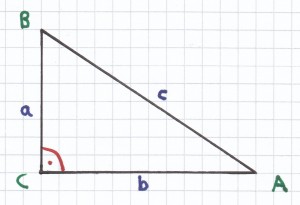
Bei diesem Dreieck ist der rechte Winkel bei C und die Hypotenuse bei c.
Die Bestimmung der Hypotenuse mittels des Satz des Pythagoras ist daher: a² + b² = c²
Die Bestimmung einer der beiden Katheten mithilfe das Satz des Pythagoras ist deshalb: c² – b² = a²
Die Bestimmung der anderen Kathete mittels des Satz des Pythagoras lautet: c² – a² = b²
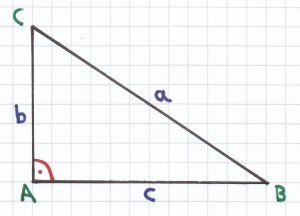
Bei diesem Dreieck ist der rechte Winkel bei A und somit die Hypotenuse bei a.
Die Ermittlung der Hypotenuse mit dem Satz des Pythagoras ist: b² + c² = a²
Die Ermittlung einer Kathete mit dem Satz des Pythagoras ist: a² – b² = c²
Die Bestimmung der zweiten Kathete mit dem Satz des Pythagoras ist: a² – c² = b²
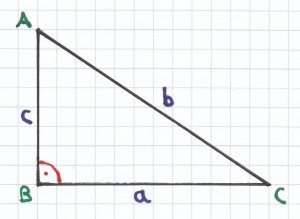
Der rechte Winkel ist hier bei B und somit die Hypotenuse bei b.
Daher ergibt sich für die Hypotenuse mithilfe des Satz des Pythagoras: a² + c² = b²
Deshalb kann man eine Kathete mit dem Satz des Pythagoras wie folgt ermitteln: b² – c² = a²
Die andere Kathete kann man mithilfe des Satz des Pythagoras folgendermaßen berechnen: b² – a² = c²
2. Mathematik-Nachhilfe-Aufgabe: Berechne, wie hoch eine Leiter angelehnt ist.
Eine Leiter besitzt eine Länge von 4,20 m. Diese lehnt an einer Mauer. Das Fußende der Leiter ist von der Mauer 2,20 m entfernt. Fertige zuerst eine Skizze an.
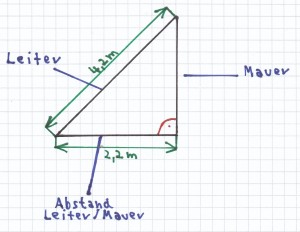
Durch die Skizze wird deutlich, dass zwischen Leiter, Mauer und deren Abstand am unteren Ende ein rechtwinkliges Dreieck entsteht. Hierbei bildet die Leiter die Hypotenuse. Die Höhe der Mauer und der Abstand zwischen Mauer und Leiter sind daher die Katheten des Dreiecks.
Mithilfe des Satz des Pythagoras kann man die Höhe der Mauer folgendermaßen berechnen:
Mauer² = Leiter² – Abstand²
[latexpage] $Mauer^2$ = $(4,2~m)^2$ – [latexpage]$(2,2~m)^2$
[latexpage] $Mauer^2$ = 17,64 m² – 4,84 m²
[latexpage] $Mauer^2$ = 12,8 m² | √ <=>
Mauer = $\sqrt{(12,8~m^2)}$ <=>
Mauer = 3,58 m (gerundet auf zwei Nachkommastellen)
Die Leiter ist auf einer Höhe von 3,58 m an der Mauer angelehnt.
3. Mathe-Nachhilfe-Aufgabe: Bilde folgende Strecken mithilfe des Satz des Pythagoras.
a) [latexpage] $\sqrt{\ {10}$
Eine Strecke besteht aus zwei Punkten. Wenn man eine Strecke mithilfe des Satz des Pythagoras bilden möchte, ist diese auf jeden Fall eine Seite des rechtwinkligen Dreiecks, und hier auf jeden Fall die Hypotenuse. Schließlich ist eine Strecke gesucht, die aufgrund der Wurzel eine besondere Zahl vorweist. Quadriert man beim Satz des Pythagoras die beiden Katheten und zieht anschließend die Wurzel, so erhält man die Hypotenuse, die eine Wurzel vorweist und auch eine Seite bzw. Strecke ist.
Man muss also zwei Seiten quadrieren und anschließend die Wurzel ziehen. Hierbei muss natürlich [latexpage] $\sqrt{\ {10}$ herauskommen.
Das geht folgendermaßen, wenn eine Seite 3 (cm, mm…) lang ist und die andere Seite 1 (cm, mm…).
[latexpage] $\sqrt{\ {3^2+1^2}$ = $\sqrt{\ {9+1}$ = $\sqrt{\ {10}$
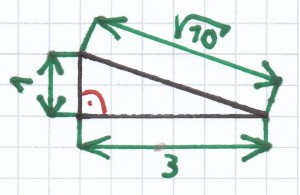
Man muss einfach ein wenig ausprobieren, welche quadrierten Zahlen zusammen die Zahl unter der Wurzel ergeben.
b) [latexpage] $\sqrt{\ {20}$
Das geht hier, wenn eine Seite 4 (cm, mm…) lang ist und die andere Seite 2 (cm, mm…).
[latexpage] $\sqrt{\ {4^2+2^2}$ = $\sqrt{\ {16+4}$ = $\sqrt{\ {20}$
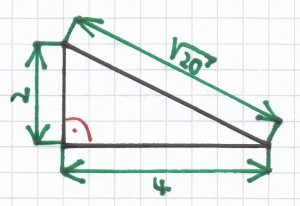
c) [latexpage] $\sqrt{\ {2}$
Hier müssen beide Seiten jeweils 1 (cm, mm…) lang sein.
[latexpage] $\sqrt{\ {1^2+1^2}$ = $\sqrt{\ {1+1}$ = $\sqrt{\ {2}$
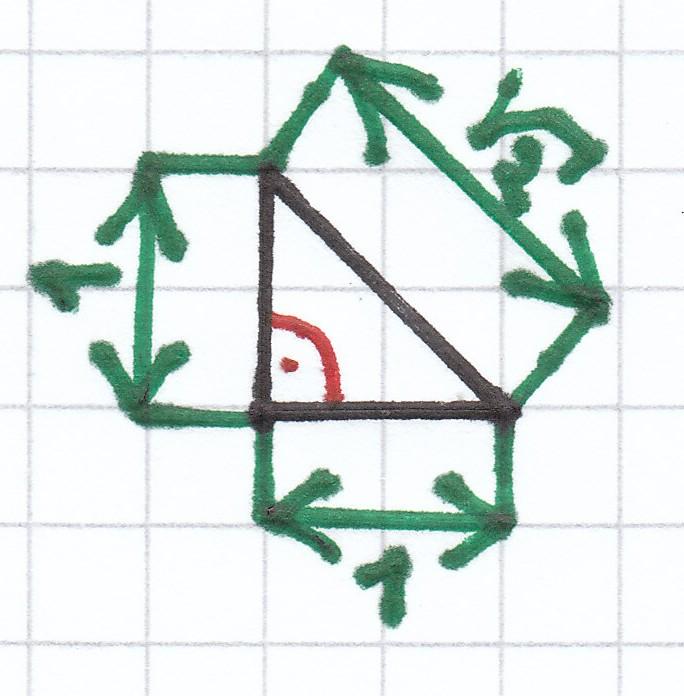
4. Mathematik-Nachhilfe-Aufgabe: Bestimme mittels des Satz des Pythagoras ein Quadrat, das diesen Flächeninhalt hat.
a) A = 2 cm²
Bei dem Satz des Pythagoras handelt es sich ja um eine Flächen-Gleichung, die aus drei Flächen-Quadraten besteht. Hierbei sind die beiden Flächenquadrate der beiden Katheten gleich dem Flächenquadrat der Hypotenuse. Um nun die Aufgabe lösen zu können, muss man quadrierte Seitenlängen der Katheten finden, die zusammen den gesuchten Flächeninhalt des Quadrats ergeben; oder man muss eine quadrierte Hypotenuse, von der man eine quadrierte Kathete abzieht, finden, das Ergebnis muss dann den Flächeninhalt des gesuchten Quadrats sein.
Hier ist das bei der Seitenlänge 1 cm und der Seitenlänge 1 cm der Katheten gewährleistet. Denn:
(1 cm)² + (1 cm)² = 1 cm² + 1 cm² = 2 cm²
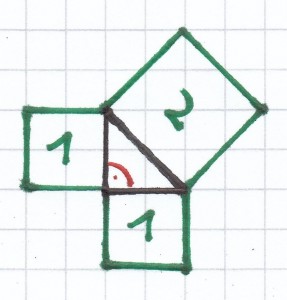
b) A = 27 cm²
Hier muss die Hypotenuse 6 cm sein und eine Seitenlänge der Kathete 3 cm. Denn:
(6 cm)² – (3 cm)² = 36 cm² – 9 cm² = 27 cm²
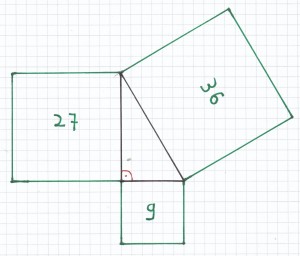
c) A = 13 cm²
Hier ist das bei den Seitenlängen 2 cm und 3 cm der Katheten der Fall. Denn:
(2 cm)² + (3 cm)² = 4 cm² + 9 cm² = 13 cm²
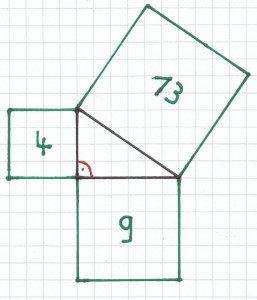
d) A = 12 cm²
Hier muss die Hypotenuse 4 cm lang sein und eine Kathete 2 cm. Denn:
(4 cm)² – (2 cm)² = 16 cm² – 4 cm² = 12 cm²
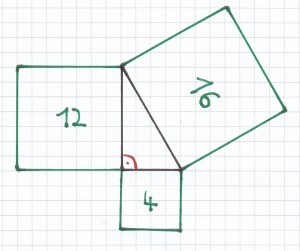
e) A = 41 cm²
Hier müsse die Katheten die Seitenlängen 4 cm und 5 cm vorweisen. Denn:
(4 cm)² + (5 cm)² = 16 cm² + 25 cm² = 41 cm²