Neben Gleichungen sind in Mathe ebenso Funktionen überaus wichtig. Beides bedingt sich ja. Eine Funktion kann ja immer auch mittels einer Gleichung wiedergegeben werden. Eine Funktion weist hierbei immer folgende Merkmale auf: Sie hat eine Definitionsmenge, eine Zuordnungsvorschrift, eine Funktionsgleichung und einen Funktionsterm. Mittels einer Wertetabelle kann oft eine Funktion in ein Koordinatensystem gezeichnet werden. Das Schaubild im Koordinatensystem nennt man Graphen der Funktion. Eine der einfachsten Funktionen ist die erste Winkelhalbierende. Diese hat die Definitionsmenge D = ℝ, die Zuordnungsvorschrift x → x, die Funktionsgleichung y = x und der Funktionsterm ist x. Der Graph dieser Funktion ist eine Gerade. Das alles sollte man bei Funktionen sehr gut verinnerlicht haben, da in der Oberstufe in der Analysis nur Funktionen analysiert werden.
Aufgaben zum Mathe-Stoffgebiet Funktionen
1. Mathematik-Nachhilfe-Aufgabe: Es sind folgende Funktionsgleichungen gegeben:
a) y = 2x – 1
b) y = x² – 2
c) y = x · (2 + x)
Für die Variable x soll der Reihe nach –3, –2, –1, 0, 1, 2, … , 8 eingesetzt werden. Ermittle die jeweiligen Werte für y. Erstelle für alle Wertepaare eine Wertetabelle. Gib ebenso den Funktionsterm und die Zuordnungsvorschrift an. Zeichne zudem die Graphen der Funktion.
2. Mathe-Nachhilfe-Aufgabe: Eine Funktion f weist diese Funktionsterme auf:
a) f(x) = 1 – x
b)
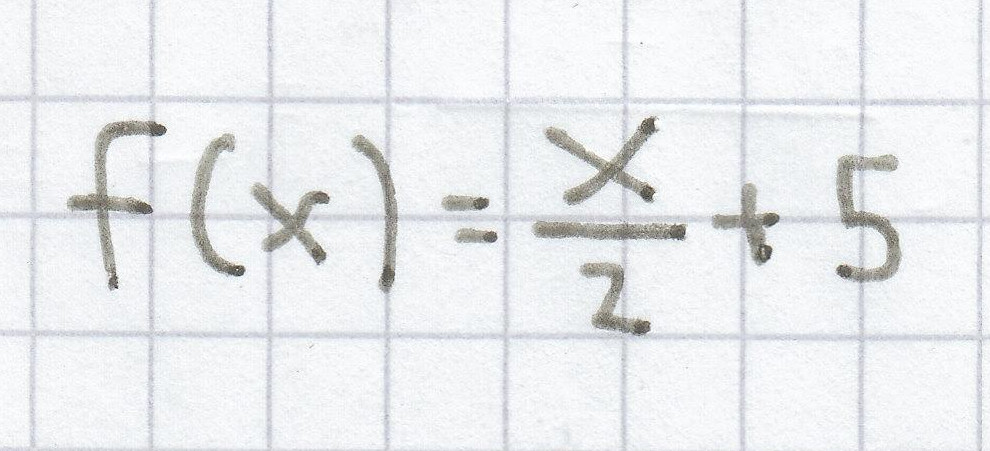
c) f(x) = 8x – 1
Ermittle jeweils die Stelle der Funktion, für die gilt:
(1) f(x) = 2
(2)
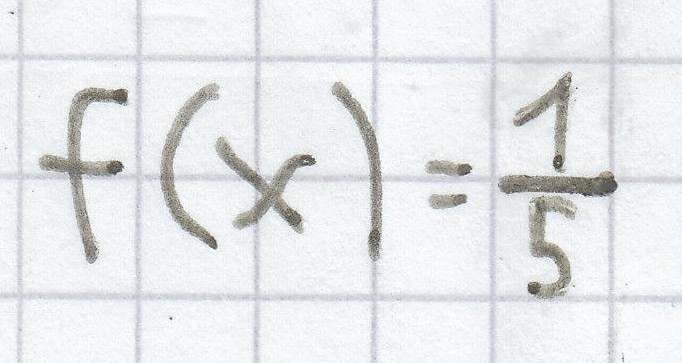
(3) f(x) = –1
(4) f(x) = 0
3. Mathematik-Nachhilfe-Aufgabe: Zeichne zunächst den Graphen der Funktion. Ermittle daraufhin die Wertemenge.
a) y = 2 · x
b) y = –x²
c) y = |x|
4. Mathe-Nachhilfe-Aufgabe: In den Funktionsterm soll der Reihe nach Folgendes eingesetzt werden: a für x, 2a für x, a – 8 für x. Vereinfache den Term dann, wenn möglich.
a) f(x) =[latexpage] ${\frac{x}{2}}$ + 4
b) f(x) = x²
c) f(x) =[latexpage] ${\frac{2}{x~+~8}}$
Lösungen zum Mathematik-Stoffgebiet Funktionen
1. Mathe-Nachhilfe-Aufgabe: Diese Funktionsgleichungen sind gegeben:
a) y = 2x – 1
b) y = x² – 2
c) y = x · (2 + x)
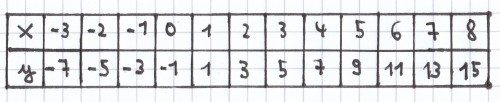
Der Reihe nach soll für die Variable x –3, –2, –1, 0, 1, 2, … , 8 eingesetzt werden. Bestimme hierdurch die sich ergebenden Werte für y. Lege hierfür auch eine Wertetabelle an. Bestimme auch den Funktionsterm und die Zuordnungsvorschrift. Zeichne zudem jeweils den Graphen der Funktion.
a) y = 2x – 1
für x = –3: y = 2 · (–3) – 1 <=> y = –6 – 1 <=> y = –7
für x = –2: y = 2 · (–2) – 1 <=> y = –4 – 1 <=> y = –5
für x = –1: y = 2 · (–1) – 1 <=> y = –2 – 1 <=> y = –3
für x = 0: y = 2 · 0 – 1 <=> y = 0 – 1 = –1
für x = 1: y = 2 · 1 – 1 <=> y = 2 – 1 = 1
für x = 2: y = 2 · 2 – 1 <=> y = 4 – 1 = 3
für x = 3: y = 2 · 3 – 1 <=> y = 6 – 1 = 5
für x = 4: y = 2 · 4 – 1 <=> y = 8 – 1 = 7
für x = 5: y = 2 · 5 – 1 <=> y = 10 – 1 = 9
für x = 6: y = 2 · 6 – 1 <=> y = 12 – 1 = 11
für x = 7: y = 2 · 7 – 1 <=> y = 14 – 1 = 13
für x = 8: y = 2 · 8 – 1 <=> y = 16 – 1 = 15
Der Funktionsterm lautet: 2x – 1
Die Zuordnungsvorschrift ist: x[latexpage] ${\mapsto}$ 2x – 1
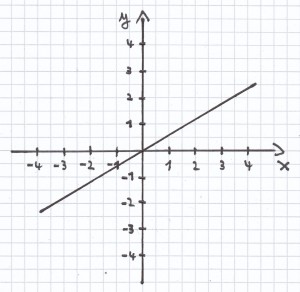
b) f(x) = x²
für x = –3: y = (–3)² = 9
für x = –2: y = (–2)² = 4
für x = –1: y = (–1)² = 1
für x = 0: y = (0)² = 0
für x = 1: y = (1)² = 1
für x = 2: y = (2)² = 4
für x = 3: y = (3)² = 9
für x = 4: y = (4)² = 16
für x = 5: y = (5)² = 25
für x = 6: y = (6)² = 36
für x = 7: y = (7)² = 49

Der Funktionsterm ist hier: x²
Die Zuordnungsvorschrift ist: x[latexpage] ${\mapsto}$ x²
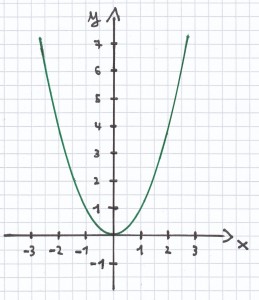
c) y = x · (2 + x) <=> y = x · 2 + x · x <=> y = x² + 2x
für x = –3: y = (–3)² + 2 · (–3) <=> y = 9 – 6 <=> y = 3
für x = –2: y = (–2)² + 2 · (–2) <=> y = 4 – 4 <=> y = 0
für x = –1: y = (–1)² + 2 · (–1) <=> y = 1 – 2 <=> y = –1
für x = 0: y = (0)² + 2 · (0) <=> y = 0 + 0 <=> y = 0
für x = 1: y = (1)² + 2 · 1 <=> y = 1 + 2 <=> y = 3
für x = 2: y = (2)² + 2 · 2 <=> y = 4 + 4 <=> y = 8
für x = 3: y = (3)² + 2 · 3 <=> y = 9 + 6 <=> y = 15
für x = 4: y = (4)² + 2 · 4 <=> y = 16 + 8 <=> y = 24
für x = 5: y = (5)² + 2 · 5 <=> y = 25 + 10 <=> y = 35
für x = 6: y = (6)² + 2 · 6 <=> y = 36 + 12 <=> y = 48
für x = 7: y = (7)² + 2 · 7 <=> y = 49 + 14 <=> y = 63
für x = 8: y = (8)² + 2 · 8 <=> y = 64 + 16 <=> y = 80
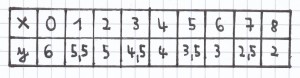
Der Funktionsterm ist hier: x · (2 + x)
Die Zuordnungsvorschrift lautet hier: x[latexpage] ${\mapsto}$ x · (2 + x)
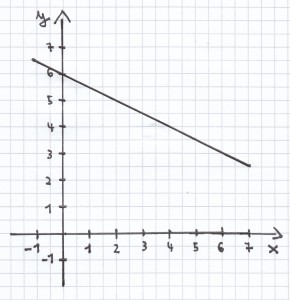
2. Mathematik-Nachhilfe-Aufgabe: Es sind folgende Funktionsterme einer Funktion f gegeben:
a) f(x) = 1 – x
b)
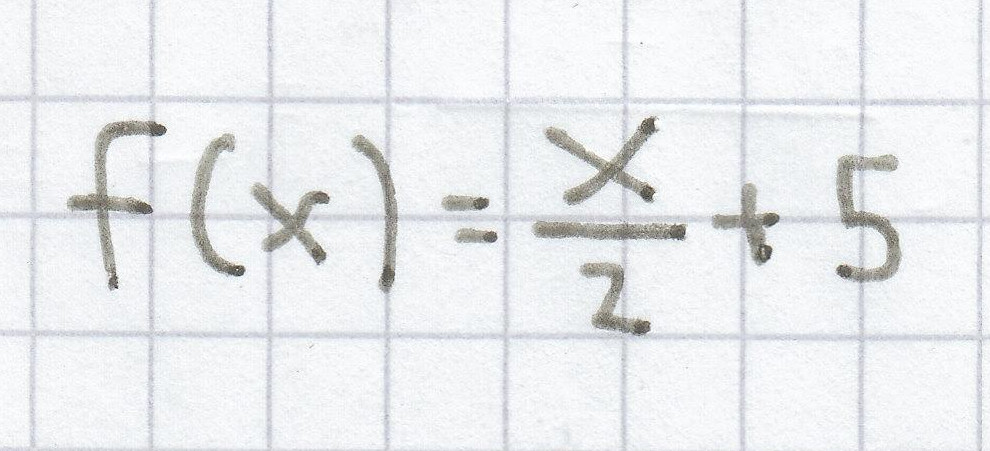
c) f(x) = 8x – 1
Bestimme die Stelle der Funktion, für die gilt:
(1) f(x) = 2
(2)
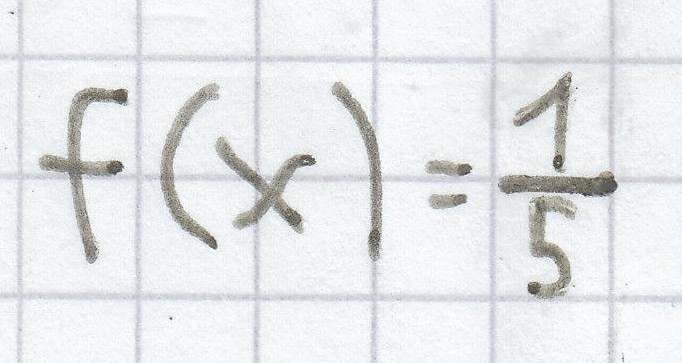
(3) f(x) = –1
(4) f(x) = 0
Die Funktionswerte, die gegeben sind, sind jeweils die y-Werte der Funktion. Es soll hierzu nun der dazugehörige x-Wert ermittelt werden. Es muss nun einfach für f(x) der y-Wert eingesetzt werden und die hieraus sich ergebende Gleichung nach x hin aufgelöst werden.
a) f(x) = 1 – x
(1) f(x) = 2
2 = 1 – x | – 1 <=>
1 = –x | · (–1) <=>
–1 = x <=>
x = –1
An der Stelle x = –1 ist f(x) = 2
(2) f(x) =[latexpage] ${\frac{1}{5}}$
${\frac{1}{5}}$ = 1 – x | – 1 <=>
–${\frac{4}{5}}$ = –x | · (–1) <=>
${\frac{4}{5}}$ = x <=>
x = ${\frac{4}{5}}$
An der Stelle x = ${\frac{4}{5}}$ ist f(x) = ${\frac{1}{5}}$
(3) f(x) = –1
–1 = 1 – x | – 1 <=>
–2 = –x | · (–1) <=>
2 = x
An der Stelle x = 2 ist f(x) = –1
(4) f(x) = 0
0 = 1 – x | + x <=>
x = 1
An der Stelle x = 1 ist f(x) = 0
b) [latexpage] ${\frac{x}{2}}$ + 5
(1) f(x) = 2
2 = ${\frac{x}{2}}$ + 5 | – 5 <=>
–3 = ${\frac{x}{2}}$ | · 2 <=>
–6 = x <=>
x = –6
An der Stelle x = –6 ist f(x) = 2
(2) f(x) =[latexpage] ${\frac{1}{5}}$
${\frac{1}{5}}$ = ${\frac{x}{2}}$ + 5 | – 5 <=>
–4,8 = ${\frac{x}{2}}$ | · 2 <=>
–9,6 = x <=>
x = –9,6
An der Stelle x = –9,6 ist y = ${\frac{1}{5}}$
(3) f(x) = –1
–1 = ${\frac{x}{2}}$ + 5 | – 5 <=>
–6 = ${\frac{x}{2}}$ | · 2 <=>
–12 = x <=>
x = –12
An der Stelle x = –12 ist f(x) = –1
(4) f(x) = 0
0 = ${\frac{x}{2}}$ + 5 | – 5 <=>
–5 = ${\frac{x}{2}}$ | · 2 <=>
–10 = x <=>
x = –10
An der Stelle x = –10 ist y = 0
c) f(x) = 8x – 1
(1) f(x) = 2
2 = 8x – 1 | + 1 <=>
3 = 8x | : 8 <=>
${\frac{3}{8}}$ = x <=>
x = ${\frac{3}{8}}$
An der Stelle x = ${\frac{3}{8}}$ ist f(x) = 2
(2) f(x) =[latexpage] ${\frac{1}{5}}$
${\frac{1}{5}}$ = 8x – 1 | + 1 <=>
1,2 = 8x | : 8 <=>
0,15 = x <=>
x = 0,15
An der Stelle x = 0,15 ist f(x) = ${\frac{1}{5}}$
(3) f(x) = –1
–1 = 8x – 1 | + 1 <=>
0 = 8x | : 8 <=>
0 = x <=>
x = 0
An der Stelle x = 0 ist f(x)= –1
(4) f(x) = 0
0 = 8x – 1 | + 1 <=>
1 = 8x | : 8 <=>
0,125 = x <=>
x = 0,125
An der Stelle x = 0,125 ist f(x) = 0
3. Mathe-Nachhilfe-Aufgabe: Zeichne zunächst den Graphen der Funktion. Bestimme anschließend seine Wertemenge.
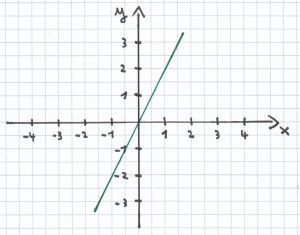
Wie man sieht, verläuft die Funktion sowohl im negativen Bereich als auch im positiven Bereich. Daher ist W = ℝ.
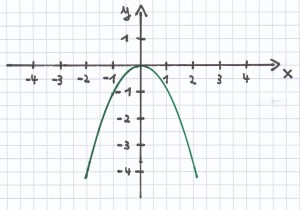
Wie man sieht, verläuft die Funktion nur im negativen Bereich. Die Zahl Null ist aber auch dabei. Daher ist hier: W = ℝ0–}$ (das heißt: alle negativen reellen Zahlen inklusive der Null).
c) y = |x|
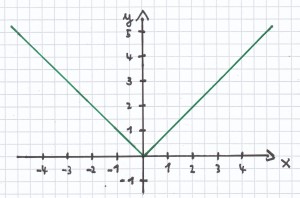
Wie man sieht, verläuft die Funktion nur im positiven Bereich inklusive der Zahl Null. Der Wertebereich ist deshalb: W = ℝ0+ (das heißt: alle positiven reellen Zahlen inklusive der Null).
4. Mathematik-Nachhilfe-Aufgabe: Setze in den Funktionsterm der Reihe nach Folgendes: a für x, 2a für x, a – 8 für x. Wenn möglich, vereinfache dann den Term.
a) f(x) =[latexpage] ${\frac{x}{2}}$ + 4
b) f(x) = x²
c) f(x) =[latexpage] ${\frac{2}{x~+~8}}$
a) f(x) =[latexpage] ${\frac{x}{2}}$ + 4
a für x: f(a) =[latexpage] ${\frac{a}{2}}$ + 4
2a für x: f(a) =[latexpage] ${\frac{2a}{2}}$ + 4 <=>
Hier kann man sowohl im Zähler als auch im Nenner die „2“ herauskürzen.
f(a) a + 4
a – 8 für x: f(a) =[latexpage] ${\frac{a-8}{2}}$ + 4 <=>
Hier kann man den Zähler jeweils durch „2“ teilen.
f(a) = ${\frac{1}{2}}$a – 4 + 4 <=>
f(a) = ${\frac{1}{2}}$a
b) f(x) = x²
a für x: f(a) = a²
2a für x: f(a) = (2a)² <=>
f(a) = 4a²
a – 8 für x: f(a) = (a – 8)² <=>
f(a) = a² + 2 · a · (–8) + (–8)² <=>
f(a) = a² – 16a + 64
c) f(x) =[latexpage] ${\frac{2}{x~+~8}}$
a für x: f(a) =[latexpage] ${\frac{2}{a~+~8}}$
2a für x: f(a) =[latexpage] ${\frac{2}{2a~+~8}}$ <=>
f(a) $\frac{2\ {\cdot}\ 1}{2\ {\cdot}\ (a~+~4)}$ <=>
Hier kann man den Faktor „2“ ausklammern und dann kürzen.
f(a) =[latexpage] ${\frac{1}{a~+~4}}$
a – 8 für x: f(a) =[latexpage] ${\frac{2}{a~-~8~+~8}}$ <=>
f(a) =[latexpage] ${\frac{2}{a}}$