
Terme sind in Mathe Ausdrücke, die man auf bestimmte algebraische Weise verändern kann. Hierfür gibt es eine Vielzahl von Regeln. Je öfter man die Regeln bei verschiedenen Termen anwendet, desto mehr gehen diese „in Fleisch und Blut über“. Je nach Aufgabe muss man einen Term aber auch erst aufstellen. Liegt eine Textaufgabe vor, so muss man nämlich erst die dort dargelegten schriftsprachlichen Informationen in die Sprache der Mathematik übertragen. Der Schwierigkeitsgrad ist hier in der Regel etwas höher. Man muss ja den dargelegten Zusammenhang verstehen und auch wissen, wie man diesen in einem Term wiedergeben kann. Daher kommt es nicht von ungefähr, dass viele Schülerinnen und Schüler in Mathe Textaufgaben nicht sooo mögen.
Aufgaben zum Mathe-Stoffgebiet Term
1. Mathematik-Nachhilfe-Aufgabe: Das Handschütteln von Menschen ist ein Phänomen, das man mittels der Mathematik beschreiben kann. Ermittle hierzu jeweils:
a) Auf einer Familienfeier sind 2 Familienmitglieder [3 Familienmitglieder; 4 Familienmitglieder; 5 Familienmitglieder, 1 Familienmitglied]. Während der Begrüßung gibt jedes Familienmitglied jedem anderen jeweils die Hand. Wie oft wurde die Hand geschüttelt? Gib mittels Zahlen, die jeweils ein Familienmitglied symbolisieren, und deren Verbindungsstrecken, die die Anzahl des Handschüttelns aufzeigt, alle auftretenden „Handschüttel-Möglichkeiten“ wieder.
b) Die jeweils genaue „Handschüttel-Anzahl“ kann mittels des Terms 0,5 · n · (n – 1) berechnet werden. Das n steht hierbei für die Anzahl der Familienmitglieder. Setz in den Term jeweils die Anzahl an Familienmitglieder aus Aufgabe a) ein und bestätige hierdurch die ermittelnden Ergebnisse.
c) Wie oft geben sich 120 Familienmitglieder die Hand?
d) Lege dar, ob der Term auch für 0 Personen gilt.
2. Mathe-Nachhilfe-Aufgabe: Andrea hat unteren Schmuck aus Draht selbst gebastelt.
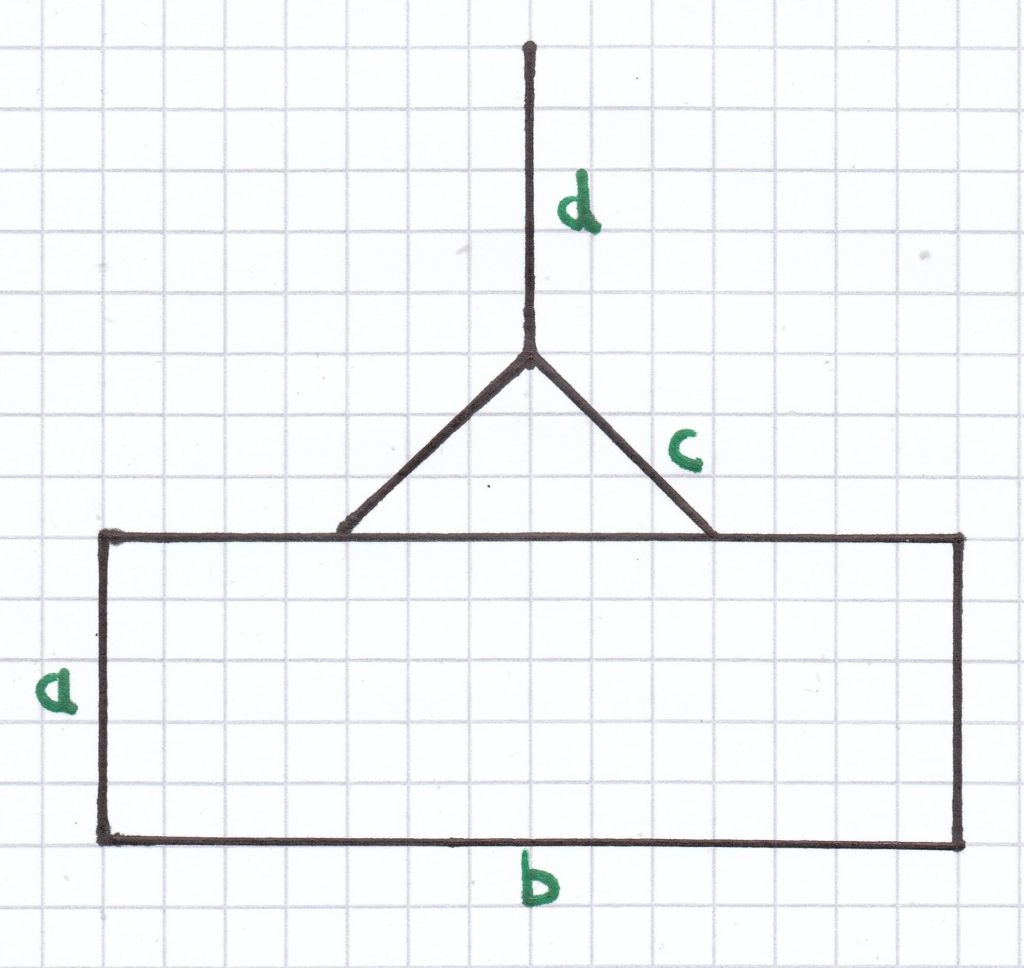
a) Stelle für den verwendeten Draht einen Term auf.
b) Berechne den Wert des Terms für:
(1) a = 9,5; b = 5,5; c = 4,6; d = 12
(2) a = 14,3; b = 9,6; c = 7,9; d = 24,1
3. Mathematik-Nachhilfe-Aufgabe: Gib folgende Textaufgabe in einem Term wieder.
a) Substrahiere die Differenz aus y und x von dem Dreifachen von x.
b) Multipliziere 4 mit x und subtrahiere davon y.
c) Multipliziere die Differenz aus x und y mit 4.
d) Bilde die Differenz aus dem 4-Fachen von x und dem Vierfachen von y.
Lege dar, bei welchen Termen man durch geschicktes Einsetzen den gleichen Term-Wert erhält. Bei welchem Term trifft das nicht zu?
4. Mathe-Nachhilfe-Aufgabe: Vereinfache die Terme.
a) x² – 20x² + 1 – y²
b) 6a + 8b – 4b
c) 1 – s – s + 16s
d) 8x + 9y + 6x
e) 5m + 7n – 3n
Lösungen zum Mathematik-Stoffgebiet Term
1. Mathe-Nachhilfe-Aufgabe: Beim Handschütteln von Personen kann man die Mathematik heranziehen. Bestimme hierbei:
a) Es sind bei einer Familienfeier 2 Familienmitglieder [3 Familienmitglieder; 4 Familienmitglieder; 5 Familienmitglieder; 1 Familienmitglied] zu Besuch. Während man sich begrüßt, gibt jedes Familienmitglied dem anderen die Hand. Stelle fest, wie oft jeweils die Hand geschüttelt wurde. Zeige das derart auf, indem Zahlen jeweils für Familienmitglieder stehen, und Verbindungsstrecken zwischen den Familienmitgliedern, die alle Möglichkeiten des Handschüttelns aufzeigen sollen.
Bei dem unteren Bild sind alle Möglichkeiten von 1 bis 4 Familienmitgliedern und deren Handschüttel-Möglichkeiten aufgezeigt.
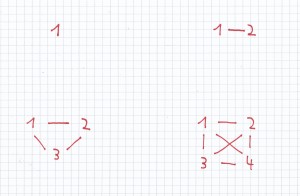
Bei einem Familienmitglied wird 0-mal die Hand geschüttelt.
Bei 2 Familienmitgliedern wird 1-mal die Hand geschüttelt.
Bei 3 Familienmitgliedern wird 3-mal die Hand geschüttelt.
Bei 4 Familienmitgliedern wird 6-mal die Hand geschüttelt.
Folgendes Bild zeigt alle Handschüttel-Möglichkeiten bei 5 Familienmitgliedern an:
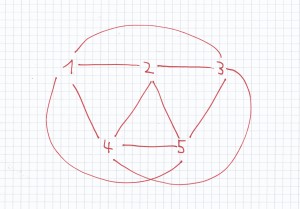
Bei 5 Familienmitgliedern wird 10-mal die Hand geschüttelt.
b) Die genaue Anzahl an „Handschüttel-Möglichkeiten“ kann man in Mathematik mit dem Term 0,5 · n · (n – 1) berechnen. Das n beinhaltet hierbei die jeweilige Anzahl an Familienmitgliedern. Bestätige alle Ergebnisse aus Aufgabe a), indem du alle möglichen Familienmitglieder in den Term einsetzt.
Bei 1 Familienmitglied: 0,5 · 1 · (1 – 1) = 0,5 · (0) = 0
Bei 2 Familienmitgliedern: 0,5 · 2 · (2 – 1) = 1 · (1) = 1
Bei 3 Familienmitgliedern: 0,5 · 3 · (3 – 1) = 1,5 · (2) = 3
Bei 4 Familienmitgliedern: 0,5 · 4 · (4 – 1) = 2 · (3) = 6
Bei 5 Familienmitgliedern: 0,5 · 5 · (5 – 1) = 2,5 · (4) = 10
Alle rechnerischen Ergebnisse stimmen mit den zeichnerischen überein.
c) Wie hoch ist die Anzahl an Handschütteln bei 120 Familienmitgliedern?
Bei 120 Familienmitgliedern: 0,5 · 120 · (120 – 1) = 60 · (119) = 7140
Bei 120 Familienmitgliedern wird 7140-mal die Hand geschüttelt.
d) Begründe, ob der Term auch bei 0 Personen ein richtiges Ergebnis liefert.
Bei 0 Familienmitgliedern: 0,5 · 0 · (0 – 1) = 0 · (–1) = 0
Der Term liefert auch bei 0 Familienmitgliedern das richtige Ergebnis, da ja dann auch 0-mal die Hand geschüttelt wird.
2. Mathematik-Nachhilfe-Aufgabe: Andrea hat mittels Draht einen Schmuck gebastelt.

a) Gib die Menge an verwendeten Draht mittels eines Terms wieder.
b) Ermittle den Term-Wert für:
(1) a = 9,5; b = 5,5; c = 4,6; d = 12
(2) a = 14,3; b = 9,6; c = 7,9; d = 24,1
a) Der Term für die Länge des Drahts setzt sich wie folgt zusammen:
a + a + b + b + c + c + d = 2a + 2b + 2c + d
b) Folgende Term-Werte ergeben sich für den aufgestellten Term:
(1) 2 · 9,5 + 2 · 5,5 + 2 · 4,6 + 12 = 19 + 11 + 9,2 + 12 = 51,2
(2) 2 · 14,3 + 2 · 9,6 + 2 · 7,9 + 24,1 = 28,6 + 19,2 + 15,8 + 24,1 = 87,7
3. Mathe-Nachhilfe-Aufgabe: Stelle für die Textaufgabe einen Term auf.
a) Subtrahiere die Differenz aus y und x von dem Dreifachen von x.
3 · x – (y – x)
b) Multipliziere die Zahl 4 mit x und subtrahiere davon y.
4 · x – y
c) Multipliziere die Differenz aus x und y mit der Zahl 4.
(x – y) · 4
d) Bilde die Differenz aus dem 4-Fachen von x und dem 4-Fachen von y.
4 · x – 4 · y
Begründe, bei welchen Termen man durch ein geschicktes Einsetzen eine Wertgleichheit erhält, bei welchen ist das nicht der Fall.
Bei c) und d) ist das bei jeglichen Werten von x und y der Fall. Hier erhält man immer Wertgleichheit.
Bei b) und c) sowie d) ist das nur der Fall, wenn y = 0 ist. Dann erhält man auch zwischen diesen Termen eine Wertgleichheit.
Die Terme b), c) und d) können zu dem Term a) keine Wertgleichheit erzielen.
4. Mathematik-Nachhilfe-Aufgabe: Vereinfache jeden Term so weit wie möglich.
a) x² – 20x² + 1 – y² = –19x² + 1 – y² = –19x² – y² + 1
b) 6a + 8b – 4b = 6a + 4b
c) 1 – s – s + 16s = 1 + 14s = 14s + 1
d) 8x + 9y + 6x = 14x + 9y
e) 5m + 7n – 3n = 5m + 4n