
Auch im Alltag benutzt man in seinem aktiven Wortschatz Potenzen. Das ist immer der Fall, wenn man etwas sehr Schwieriges oder eine – sagen wir mal auch in Anführungszeichen – sehr schwierige Person vor sich hat. „Die Aufgabe, die ich zu bewältigen habe, ist kompliziert hoch zwölf“, sagt ein Schüler zu einem anderen. „Die Person, mit der ich zusammenarbeiten muss, nervt mich im Quadrat“, antwortet eine Frau gegenüber ihrem Freund. Diese Aufgabe oder Person ist natürlich nicht an sich in der jeweiligen Potenz so schwierig bzw. schlimm. Dennoch empfindet ein Mensch das so – was natürlich dennoch real eine sehr schwierige Situation für diese Person ist. Am besten man ist selbst potent genug, um solche immer wieder im Leben auftretenden Situationen so gut wie möglich zu meistern.
Aufgaben zum Mathe-Stoffgebiet Potenzen
1. Mathematik-Nachhilfe-Aufgabe: Löse das Produkt bei den Potenzen auf.
a) (–4,5) – 2 · (–4,5) – 7
b)
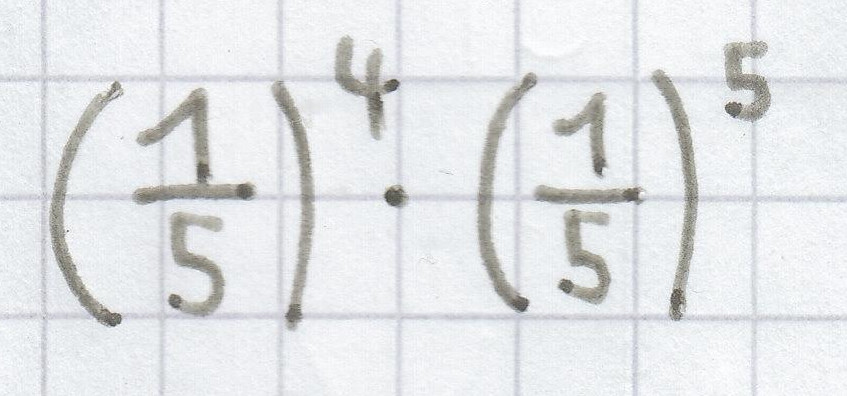
c)
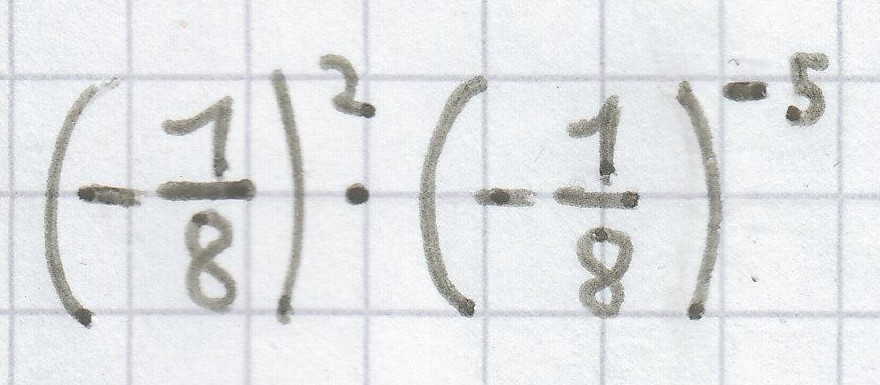
d) (3x) – 4 · (3x)2
2. Mathe-Nachhilfe-Aufgabe: Multipliziere die Klammern aus.
a) (x5 – x4 – x2) · x3
b) (4a4 + 5a5) · 3a2
c) (y – 4 – y 3 + y) · y – 2
d) 3a – 2 · b – 3 · (2a – 4 – 3b6)
3. Mathematik-Nachhilfe-Aufgabe: Ermittle das Ergebnis und vergleiche die Ergebnisse.
a) 43 + 42 und 47
b) 24 · 22 und 26
c) 54 – 52 und 52
d) 26 : 23 und 23
4. Mathe-Nachhilfe-Aufgabe: Klammere die algebraische Summe zu einem Produkt aus.
a) x4 + x2 + x
b) y3 – y5 – y
c) 22x5 + 4x3
d) 7y2 – 2y

Lösungen zum Mathematik-Stoffgebiet Potenzen
1. Mathe-Nachhilfe-Aufgabe: Berechne das Ergebnis der Potenz.
a) (–4,5) – 2 · (–4,5) – 7
Eine Potenz mit gleicher Basis multipliziert man, indem man ihre Exponenten addiert.
(–4,5) – 2 · (–4,5) – 7 = (–4,5) – 2 + (–7);
(–4,5) – 2 + (–7) = (–4,5) – 9
Einen negativen Exponenten löst man auf, indem man den Kehrtwert bildet.
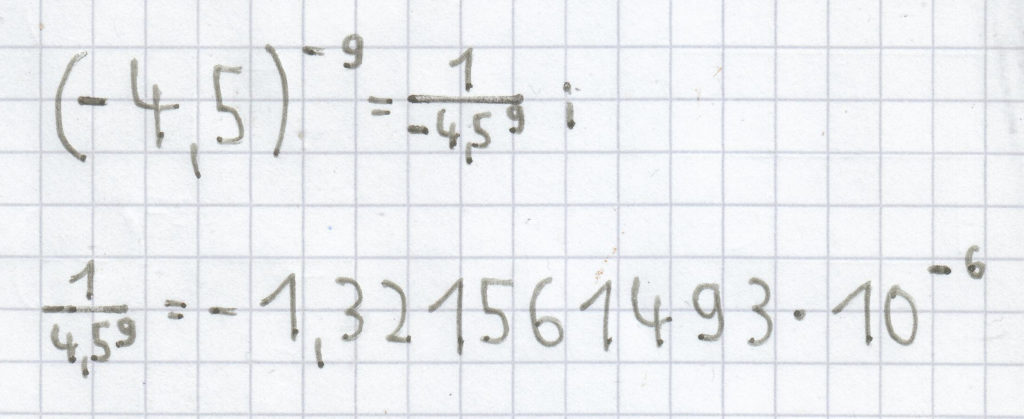
b)
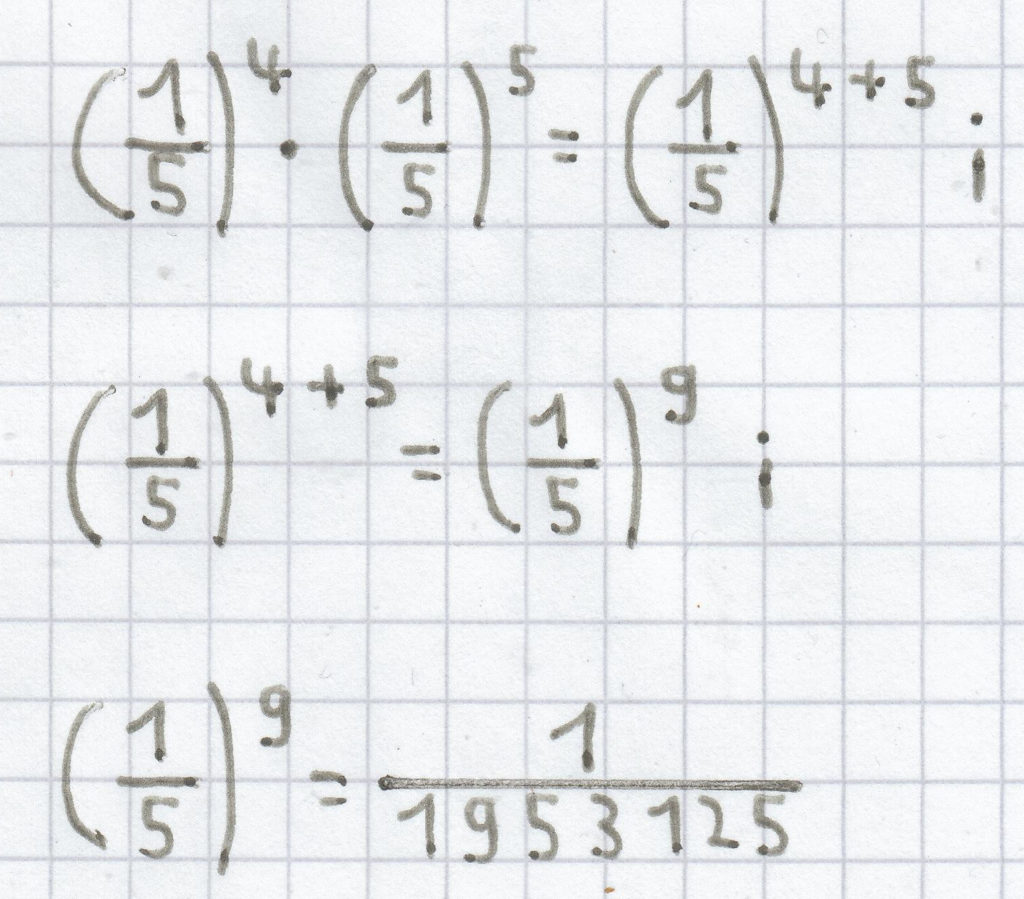
c)
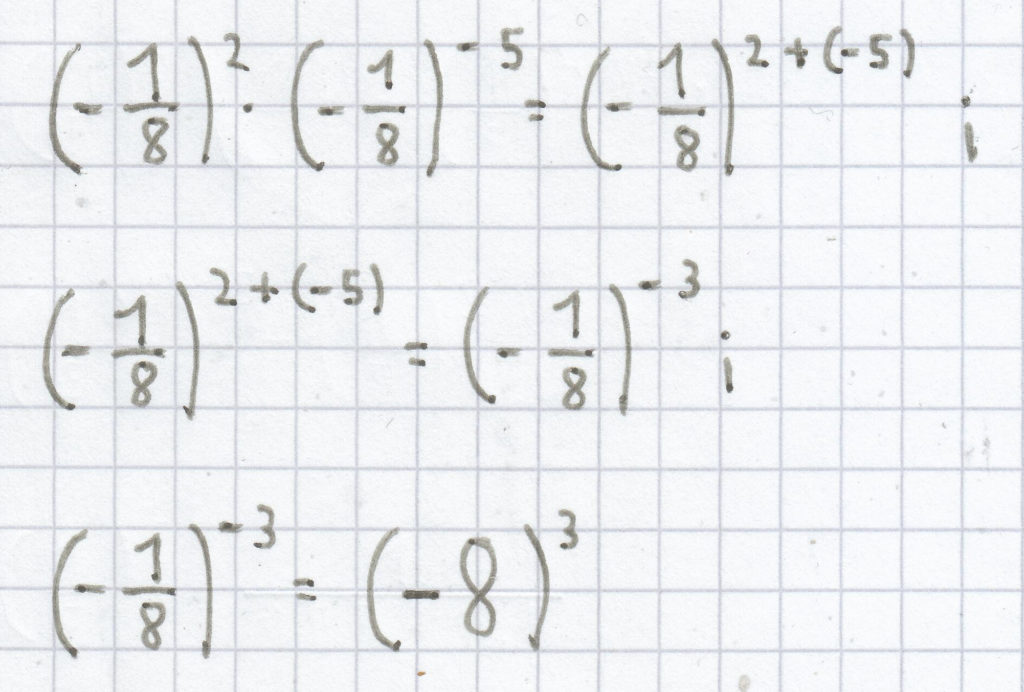
(–8)3 = –512
d)
(3x) – 4 · (3x)2 = (3x) – 4 + 2;
(3x) – 4 + 2 = (3x) – 2;
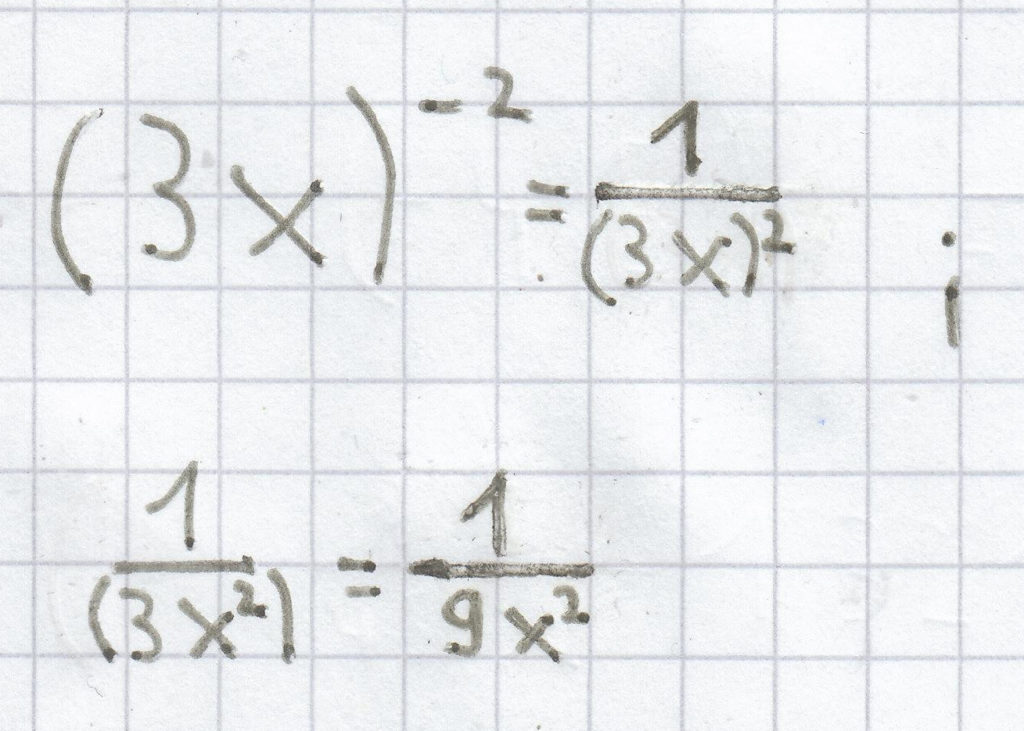
2. Mathematik-Nachhilfe-Aufgabe: Löse die Klammern mittels Ausmultiplizierens auf.
a) (x5 – x4 – x2) · x3 = x5 · x3 – x4 · x3 – x2 · x3;
x5 · x3 – x4 · x3 – x2 · x3 = x5 + 3 – x4 + 3 – x2 + 3;
x5 + 3 – x4 + 3 – x2 + 3 = x8 – x7 – x5
b) (4a4 + 5a5) · 3a2 = 4a4 · 3a2 + 5a5 · 3a2;
4a4 · 3a2 + 5a5 · 3a2 = 4 · 3a4 + 2 + 5 · 3a5 + 2;
4 · 3a4 + 2 + 5 · 3a5 + 2 = 12a6 + 15a7;
12a6 + 15a7 = 15a7 + 12a6
c) (y – 4 – y 3 + y) · y – 2 = y – 4 · y – 2 – y 3 · y – 2 + y · y – 2;
y – 4 · y – 2 – y 3 · y – 2 + y · y – 2 = y – 4 + (–2) – y 3 + (–2) + y 1 + (–2);
y – 4 + (–2) – y 3 + (–2) + y 1 + (–2) = y – 6 – y1 + y – 1;
y – 6 – y1 + y – 1 = –y + y – 1 + y – 6
d) 3a – 2 · b – 3 · (2a – 4 – 3b6) = 3a – 2 · b – 3 · 2a – 4 + 3a – 2 · b – 3 · (–3b6);
3a – 2 · b – 3 · 2a – 4 + 3a – 2 · b – 3 · (–3b6) =
3 · 2a – 2 + (–4) · b – 3 + 3 · (–3)a – 2 · b – 3 + 6;
3 · 2a – 2 + (–4) · b – 3 + 3 · (–3)a – 2 · b – 3 + 6 = 6a – 6 · b – 3 – 9a – 2 · b3;
6a – 6 · b – 3 – 9a – 2 · b3 = –9a – 2 · b3 + 6a – 6 · b – 3
3. Mathe-Nachhilfe-Aufgabe: Bestimme das Ergebnis und vergleiche untereinander die Ergebnisse.
a) 43 + 42 und 47
43 + 42 = 4 · 4 · 4 + 4 · 4;
4 · 4 · 4 + 4 · 4 = 64 + 16;
64 + 16 = 80
47 = 4 · 4 · 4 · 4 · 4 · 4 · 4;
4 · 4 · 4 · 4 · 4 · 4 · 4 = 16384
Wie man sieht, ergeben sich hier zwei sehr unterschiedliche Werte, wenn man die Potenzen auflöst. Die Addition von Potenzen mit Exponenten, die zusammen den gleichen Exponenten einer anderen Potenz ergeben, entspricht daher nicht dem Ergebnis dieser Potenz.
b) 24 · 22 und 26
24 · 22 = 2 · 2 · 2 · 2 · 2 · 2;
2 · 2 · 2 · 2 · 2 · 2 = 64
26 = 2 · 2 · 2 · 2 · 2 · 2;
2 · 2 · 2 · 2 · 2 · 2 = 64
Wie man sieht, sind hier die beiden Ergebnisse gleich. Die Multiplikation von zwei Potenzen mit gleicher Basis, deren Exponenten zusammen gleich einer Potenz mit derselben Basis und dem gleichen Exponenten sind, entsprechen sich.
c) 54 – 52 und 52
54 – 52 = 5 · 5 · 5 · 5 – 5 · 5;
5 · 5 · 5 · 5 – 5 · 5 = 625 – 25;
625 – 25 = 600
52 = 5 · 5;
5 · 5 = 25
Wie man sieht, sind hier die beiden Ergebnisse nicht identisch. Eine Subtraktion einer Potenz von einer anderen Potenz, deren Exponenten durch ein Abziehen den gleichen Exponenten ergeben, entspricht nicht dem Ergebnis dieser Potenz.
d) 26 : 23 und 23
26 : 23 = 2 · 2 · 2 · 2 · 2 · 2 : (2 · 2 · 2);
2 · 2 · 2 · 2 · 2 · 2 : (2 · 2 · 2) = 64 : 8;
64 : 8 = 8
23 = 2 · 2 · 2;
2 · 2 · 2 = 8
Wie man sieht, sind hier die Ergebnisse gleich. Die Division zweier Potenzen mit der gleichen Basis, die durch Abziehen der Exponenten die Potenz mit demselben Exponenten ergibt, entspricht sich.
4. Mathematik-Nachhilfe-Aufgabe: Die algebraische Summe soll ausgeklammert werden, dass ein Produkt entsteht.
a) x4 + x2 + x
Hier kann man das „x“ als Faktor ausklammern.
x4 + x2 + x = x · (x3 + x + 1)
b) y3 – y5 – y
Hier kann man das „y“ als Faktor ausklammern.
y3 – y5 – y = y · (y2 – y4 – 1)
c) 22x5 + 4x3
Hier kann man das „2x3“ ausklammern.
22x5 + 4x3 = 2x3 · (11x2 + 2)
d) 7y2 – 2y
Hier kann man das „y“ ausklammern.
7y2 – 2y = y · (7y – 2)