
Eine bestimmte Logik ist bei jedem Stoffgebiet in Mathe zentral. Mathematik ist ja Logik pur. Deshalb nimmt dieses Fach in der Schule auch eine sehr, sehr wichtige Stellung ein. Wie sieht nun aber beispielsweise die Logik beim Stoffgebiet Bruchgleichungen aus? Guckt man sich Bruchgleichungen an, so beginnt die Logik beim Aufstellen der Definitionsmenge der jeweiligen Aufgabe. Hiermit steht und fällt ja die Lösung der Aufgabe! Als Nächstes muss man die Gleichung dahingehend vereinfachen, dass man bei den Brüchen deren Hauptnenner bildet. Anschließend löst man die jetzt ganz normale Gleichung nach der Variablen hin auf. Zum Schluss muss man noch die Lösung mit der Definitionsmenge abgleichen und die Lösung angeben. Das ist die Logik bei Buchgleichungen – um diese Gleichungen richtig zu lösen.
Aufgaben zum Mathe-Stoffgebiet Bruchgleichungen
1. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Bruchgleichung.
a)

b)

c)
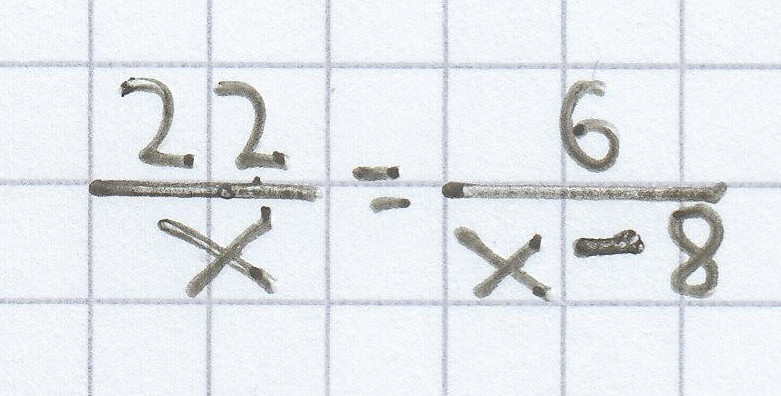
d)

2. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der Buchgleichung.
a)
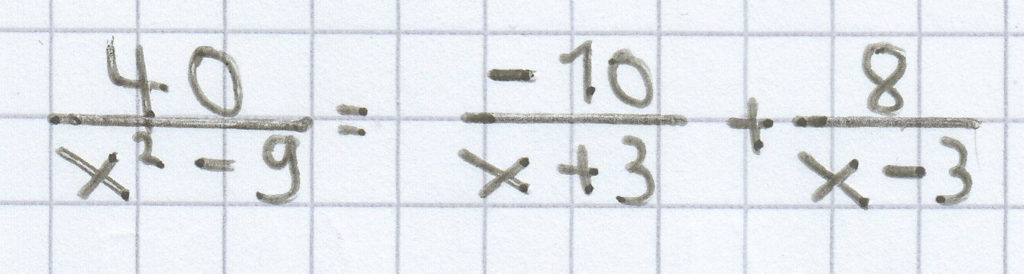
b)
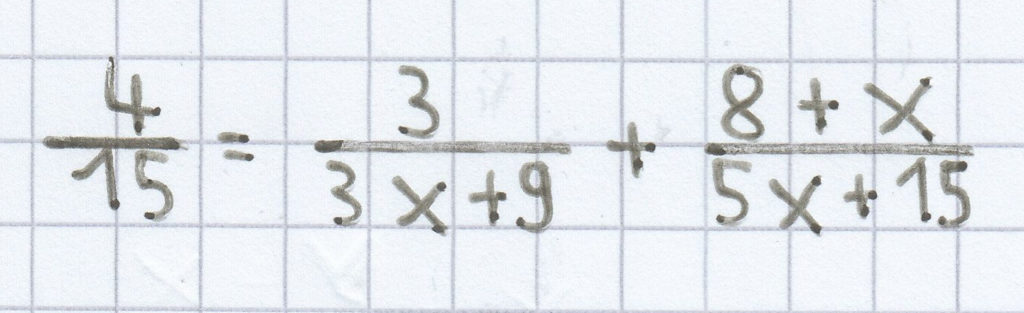
c)
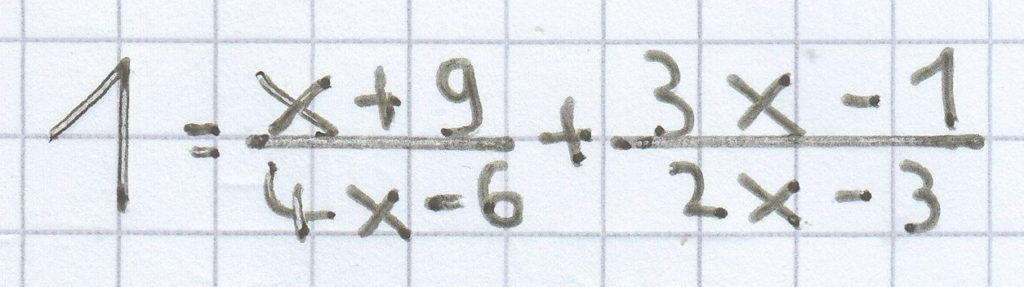
d)

3. Mathematik-Nachhilfe-Aufgabe: Lege dar, wie der Bruch der Bruchgleichung schrittweise logisch entfernt wurde.
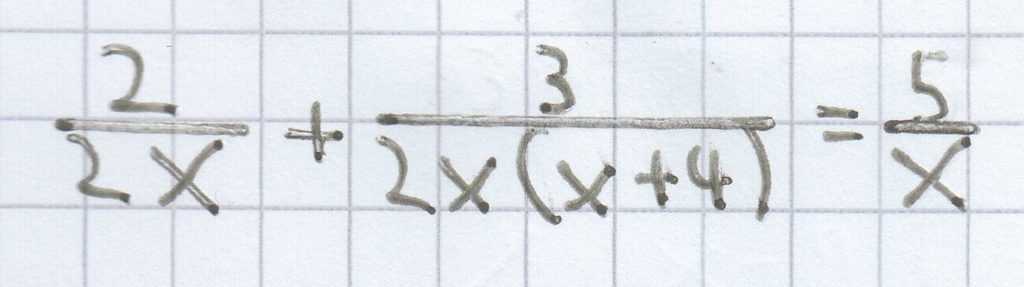
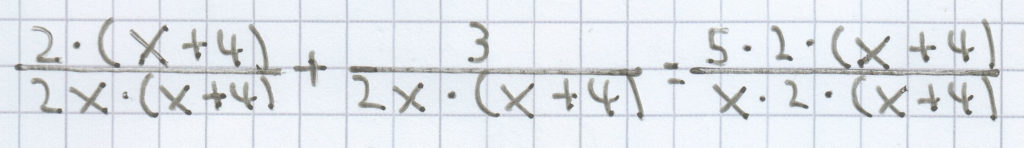
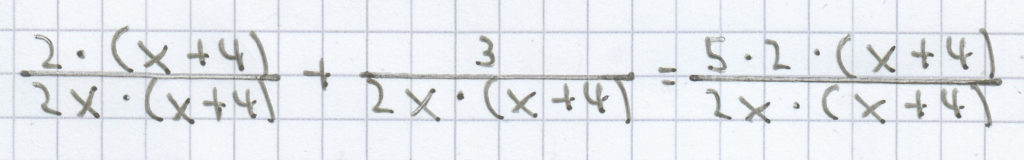
2 · (x + 4) + 3 = 5 · 2 · (x + 4)
4. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Bruchgleichung.
a)
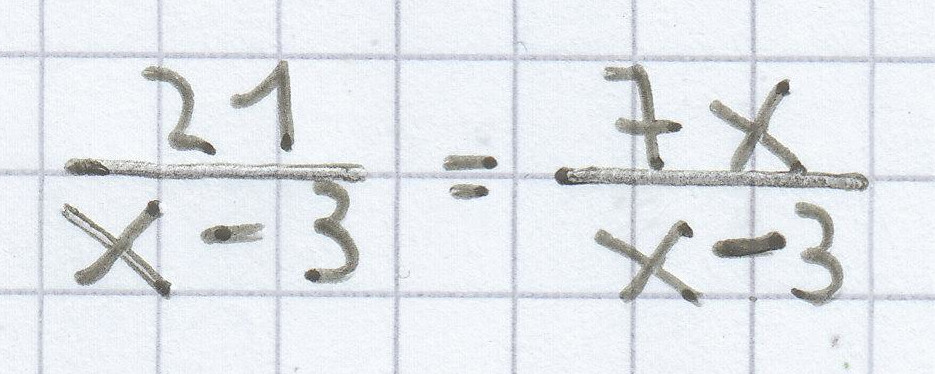
b)
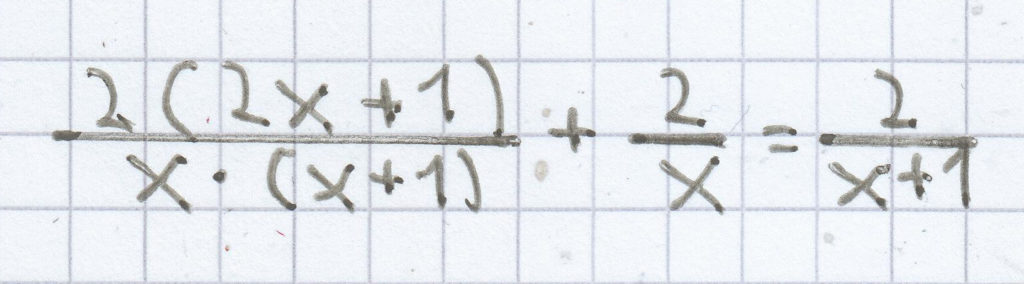
c)
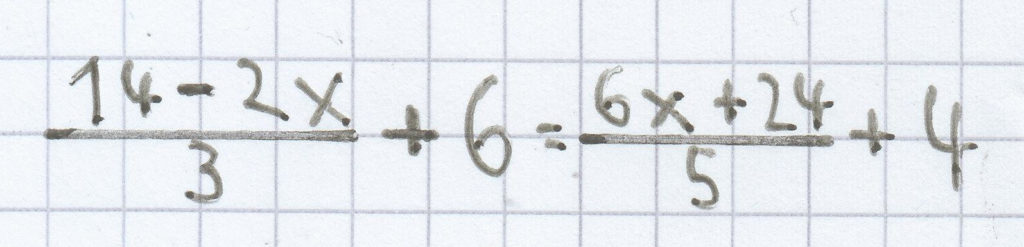
d)

Lösungen zum Mathematik-Stoffgebiet Bruchgleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle für die Lösungsmenge der Bruchgleichung.
a)

–3x + 4 = 0 | + 3x
4 = 3x | : 3

–2x + 6 = 0 | + 2x
6 = 2x | : 2
x = 3
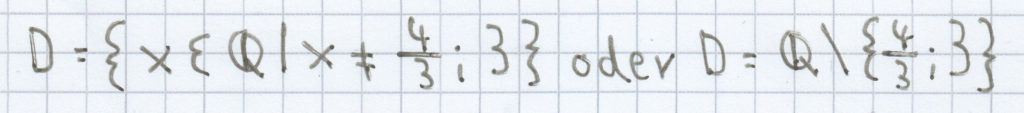
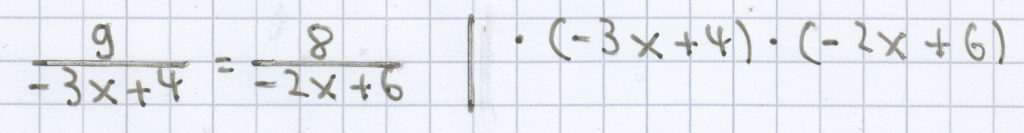
9 · (–2x + 6) = 8 · (–3x + 4)
–18x + 54 = –24x + 32 | + 24x
6x + 54 = 32 | – 54
6x = –22 | : 6


b)

2x + 5 = 0 | – 5
2x = –5 | : 2
x = –2,5
4x – 2 = 0 | + 2
4x = 2 | : 4
x = 0,5
D = {x Є ℚ | x ≠ –2,5; 0,5} oder D = ℚ \ {–2,5; 0,5}
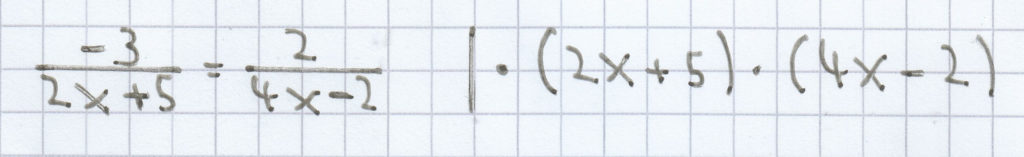
(–3) · (4x – 2) = 2 · (2x + 5)
–12x + 6 = 4x + 10 | + 12x
6 = 16x + 10 | – 10
–4 = 16x | : 16

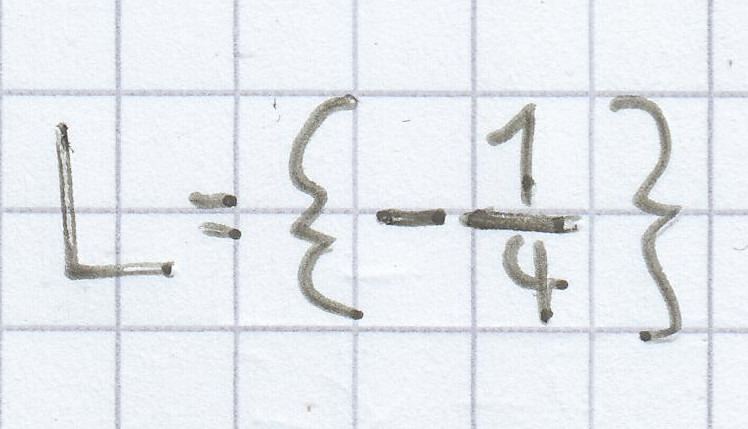
c)
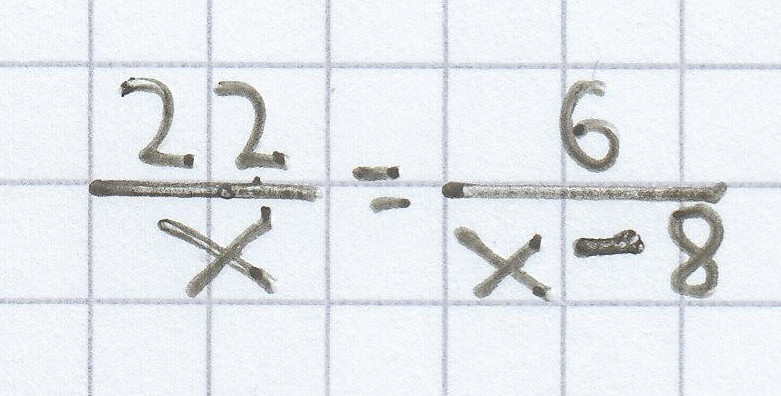
x = 0
x – 8 = 0 | + 8
x = 8
D = {x Є ℚ | x ≠ 0; 8} oder D = ℚ \ {0; 8}

22 · (x – 8) = 6 · x
22x – 176 = 6x | – 6x
16x – 176 = 0 | + 176
16x = 176 | : 16
x = 11
L = {11}
d)

–x + 2 = 0 | + x
x = 2
x + 2 = 0 | – 2
x = –2
D = {x Є ℚ | x ≠ –2; 2} oder D = ℚ \ {–2; 2}
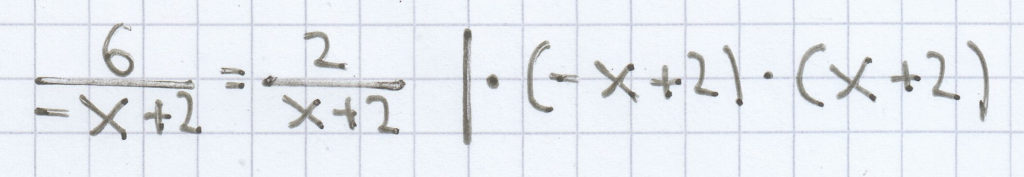
6 · (x + 2) = 2 · (–x + 2)
6x + 12 = –2x + 4 | + 2x
8x + 12 = 4 | – 12
8x = –8 | : 8
x = –1
L = {–1}
2. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Bruchgleichung.
a)
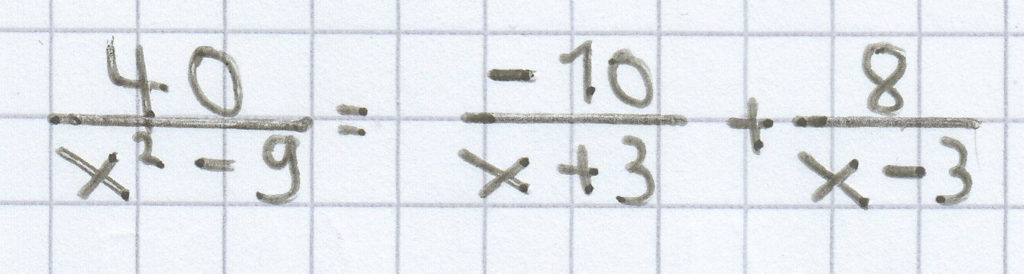
x² – 9 = (x – 3) · (x + 3)
x – 3 = 0 | + 3
x = 3
x + 3 = 0 | – 3
x = –3
D = {x Є ℚ | x ≠ –3; 3} oder D = ℚ \ {–3; 3}

40 = –10 · (x – 3) + 8 · (x + 3)
40 = –10x + 30 + 8x + 24
40 = –2x + 54 | – 54
–14 = –2x | : (–2)
x = 7
L = {7}
b)
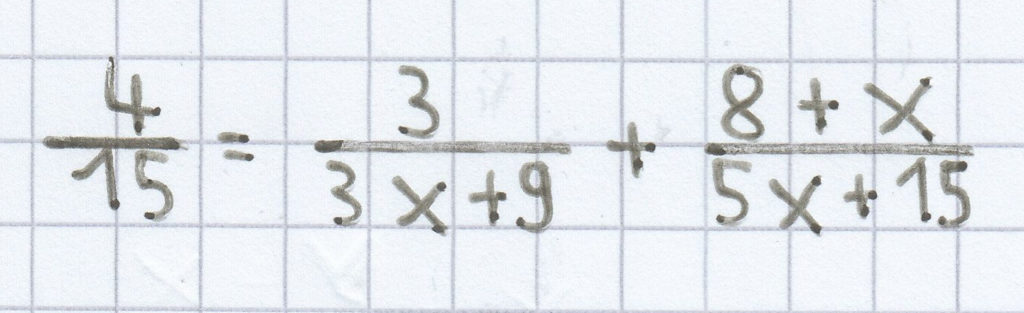
3x + 9 = 3 · (x + 3)
5x + 15 = 5 · (x + 3)
3x + 9 = 0 | – 9
3x = –9 | : 3
x = –3
5x + 15 = 0 | – 15
5x = –15 | : 3
x = –3
D = {x Є ℚ | x ≠ –3} oder D = ℚ \ {–3}
${\frac{4}{15}}$ = ${\frac{3}{3\mathrm x~+~9}}$ + ${\frac{8~+~\mathrm x}{5\mathrm x~+~15}}$
${\frac{4}{15}}$ = ${\frac{3}{3\ {\cdot}\ (\mathrm x~+~3)}}$ + ${\frac{8~+~\mathrm x}{5\ {\cdot}\ (\mathrm x~+~3)}}$
${\frac{4}{15}}$ = ${\frac{3}{3\ {\cdot}\ (\mathrm x~+~3)}}$ + ${\frac{8~+~\mathrm x}{5\ {\cdot}\ (\mathrm x~+~3)}}$ | · 15 · (x + 3)
4 · (x + 3) = 3 · 5 + (8 + x ) · 3
4x + 12 = 15 + 24 + 3x
4x + 12 = 39 + 3x | – 3x
x + 12 = 39 | – 12
x = 27
L = {27}
c)
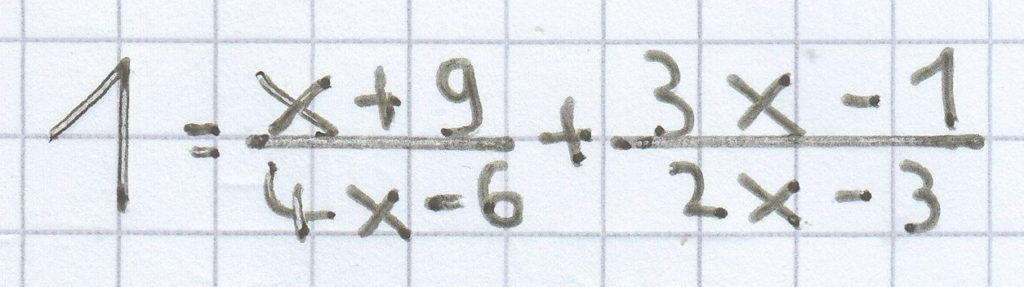
4x – 6 = 0 | + 6
4x = 6 | : 4
x = ${\frac{3}{2}}$
2x – 3 = 0 | + 3
2x = 3 | : 2
x = ${\frac{3}{2}}$
D = {x Є [latexpage]${\mathbb Q}$ | x ≠ ${\frac{3}{2}}$} oder D = ${\mathbb Q}$ \ {${\frac{3}{2}}$}
1 = ${\frac{\mathrm x~+~9}{4\mathrm x~-~6}}$ + ${\frac{3\mathrm x~-~1}{2\mathrm x~-~3}}$
1 = ${\frac{\mathrm x~+~9}{2\ {\cdot}\ (2\mathrm x~-~3)}}$ + ${\frac{3\mathrm x~-~1}{2\mathrm x~-~3}}$
${\frac{1}{-\mathrm x~+~1}}$ = ${\frac{1}{\mathrm x~-~1}}$ | · 2 · (2x – 3)
1 · 2 · (2x – 3) = x + 9 + 2 · (3x – 1)
4x – 6 = x + 9 + 6x – 2
4x – 6 = 7x + 7 | – 4x
–6 = 3x + 7 | – 7
–13 = 3x | : 3
x = –${\frac{13}{3}}$
L = {–${\frac{13}{3}}$}
d)

–x + 1 = 0 | + x
x = 1
x – 1 = 0 | + 1
x = 1
D = {x Є ℚ | x ≠ 1} oder D = ℚ \ {1}
${\frac{1}{-\mathrm x~+~1}}$ = ${\frac{1}{\mathrm x~-~1}}$
${\frac{1}{-1\ {\cdot}\ (\mathrm x~-~1)}}$ = ${\frac{1}{\mathrm x~-~1}}$ | · (–1) · (x – 1)
1 = 1 · (–1)
1 = –1
L = { } bzw. L = Ø
3. Mathe-Nachhilfe-Aufgabe: Gib an, wie der Bruch der Bruchgleichung schrittweise logisch eliminiert wurde.
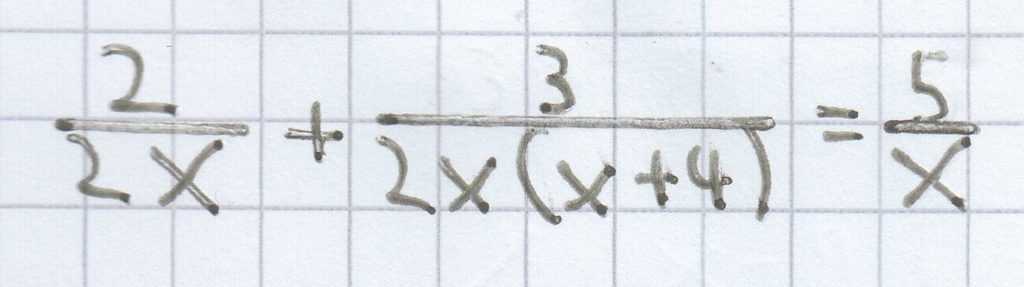
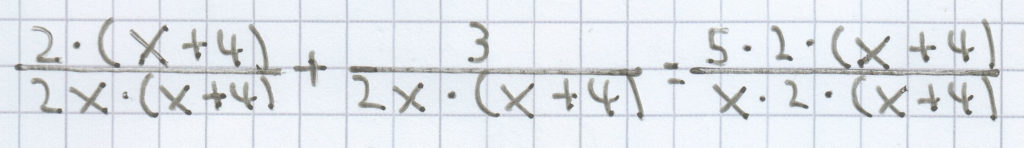
Zuerst wurden Zähler und Nenner der Brüche mit dem Hauptnenner erweitert.
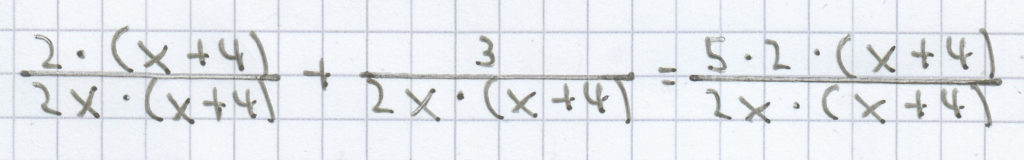
Beim letzen Bruch wurde das Vertauschungsgesetz/Kommunitativgesetz angewendet.
2 · (x + 4) + 3 = 5 · 2 · (x + 4)
Darauf wurde gekürtzt und der Nenner des Bruches entfernt.
4. Mathematik-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der Bruchgleichungen.
a)
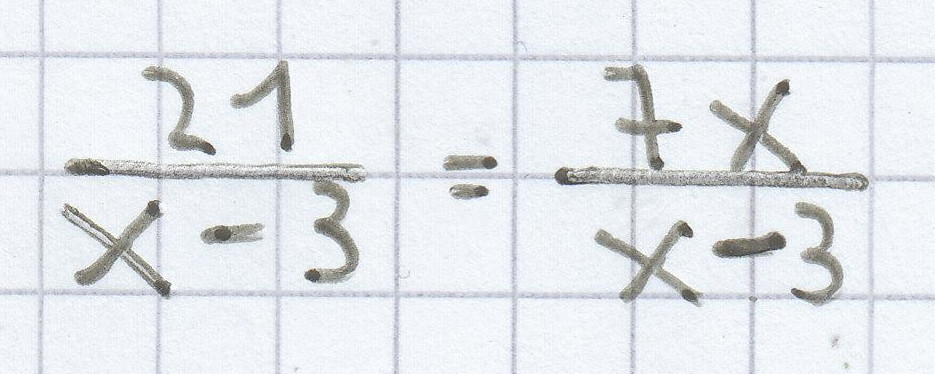
x – 3 = 0 | + 3
x = 3
D = {x Є ℚ | x ≠ 3} oder D = ℚ \ {3}
${\frac{21}{\mathrm x~-~3}}$ = ${\frac{7\mathrm x}{\mathrm x~-~3}}$ | · (x – 3)
21 = 7x | : 7
x = 3
Die Lösung gehört nicht zur Definitionsmenge!
L = { } bzw. L = Ø
b)
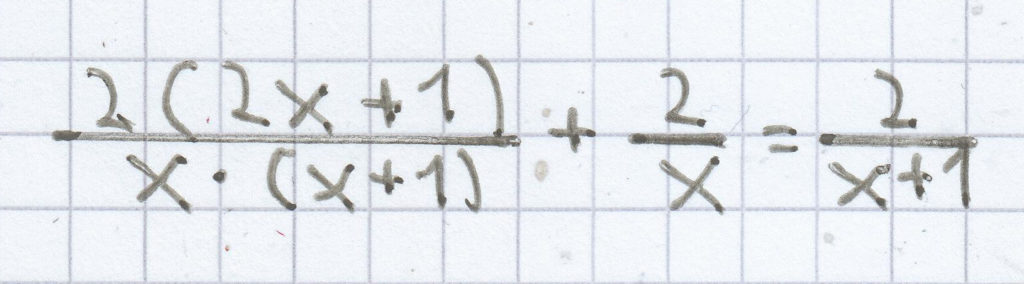
x = 0
x + 1 = 0 | – 1
x = –1
D = {x Є ℚ | x ≠ –1; 0} oder D = ℚ \ {–1; 0}
${\frac{2(2\mathrm x~+~1)}{\mathrm x(\mathrm x~+~1)}}$ + ${\frac{2}{\mathrm x}}$ = ${\frac{2}{\mathrm x~+~1}}$ | · x · (x + 1)
2 · (2x + 1) + 2 · ( x + 1) = 2 · x
4x + 2 + 2x + 2 = 2x
6x + 4 = 2x | – 6x
4 = –4x | : (–4)
x = –1
Die Lösung ist nicht zur Lösungsmenge gehörig!
L = { } bzw. L = [latexpage] ${\varnothing}$
c) ${\frac{14~-~2\mathrm x}{3}}$ + 6 = ${\frac{6\mathrm x~+~24}{5}}$ + 4 | – 4
${\frac{14~-~2\mathrm x}{3}}$ + 2 = ${\frac{6\mathrm x~+~24}{5}}$ | · 15
5 · (14 – 2x) + 15 · 2 = 3 · (6x + 24)
70 – 10x + 30 = 18x + 72
100 – 10x = 18x + 72 |+ 10x
100 = 28x + 72 | – 72
28 = 28x | : 28
x = 1
L = {1}
d) ${\frac{\mathrm x~-~3}{\mathrm x~+~4}}$ – ${\frac{\mathrm x~+~1}{\mathrm x~-~4}}$ = ${\frac{3\mathrm x}{\mathrm x^2~-~16}}$
${\frac{\mathrm x~-~3}{\mathrm x~+~4}}$ – ${\frac{\mathrm x~+~1}{\mathrm x~-~4}}$ = ${\frac{3\mathrm x}{(\mathrm x~+~4})\ {\cdot}\ (\mathrm x~-~4})}$
x + 4 = 0 | – 4
x = –4
x – 4 = 0 | + 4
x = 4
D = {x Є ℚ | x ≠ –4; 4} oder D = ℚ \ {–4; 4}
${\frac{\mathrm x~-~3}{\mathrm x~+~4}}$ – ${\frac{\mathrm x~+~1}{\mathrm x~-~4}}$ = ${\frac{3\mathrm x}{(\mathrm x~+~4})\ {\cdot}\ (\mathrm x~-~4})}$ | · (x + 4) · (x – 4)
(x – 4) · (x – 3) – (x + 4 ) · (x + 1) = 3x
x² – 3x – 4x + 12 – (x² + x + 4x + 4) = 3x
x² – 7x + 12 – (x² + 5x + 4) = 3x
x² – 7x + 12 – x² – 5x – 4 = 3x
–12x + 8 = 3x | + 12x
8 = 15x | : 15
x = ${\frac{8}{15}}$
L = {${\frac{8}{15}}$}