Wie fit man in Mathe in Algebra ist, zeigt sich augenscheinlich bei dem Stoffgebiet quadratische Funktionen. Hier muss man nämlich schon teils schwierigere Termumformungen machen. Weist nämlich eine quadratische Funktion die Form f(x) = x² + px + q auf, dann kann man beispielsweise nicht sofort sagen, wie der Scheitelpunkt der Funktion ist. Hierfür muss man den Term der Funktion algebraisch in die sogenannte Scheitelpunktform umformen. Nur dann kann man schließlich den Scheitelpunkt der Funktion eindeutig bestimmen. Um diese wichtige Termumformung in Mathe korrekt durchzuführen, muss man aber auch die binomischen Formeln gut verinnerlicht haben, da die Scheitelpunktform einen Term darstellen – bestehend aus einer binomischenen Formel. Mathe ist daher alles andere als leicht, aber auch nicht superschwer – wenn man in diesem Fach immer am Ball bleibt!
Aufgaben zum Mathematik-Stoffgebiet quadratische Funktionen
1. Mathe-Nachhilfe-Aufgabe: Bestimme den Scheitelpunkt der Funktion mittels einer Termumformung. Gib darauf an, wie man den Graphen der Funktion, ausgehend von der Normalparabel, in ein Koordinatensystem einzeichnen kann. Notiere ebenfalls, für welche x der Graph der Funktion fällt und für welche x der Graph der Funktion fällt.
a) f(x) = x² – 2x – 6
b) f(x) = x² + 4x + 4
c) f(x) = x² – 6x
d) f(x) = x² + 8x + 3
2. Mathematik-Nachhilfe-Aufgabe: Formuliere eine Gesetzmäßigkeit. Gib einen Term hierfür an.
a) Es wird die Seitenlänge eines Quadratas verdoppelt. Wie groß ist der Flächeninhalt des Quadrats?
b) Wie muss man bei einem Quadrat die Seitenlängen verändern, dass der Flächinhalt doppelt so groß wird?
3. Mathe-Nachhilfe-Aufgabe: Der Graph der Funktion soll gezeichnet werden. Es soll ebenso der Scheitelpunkt bestimmt werden sowie die Schnittpunkte mit den Koordinatenachsen.
a) f(x) = x² – 2
b) f(x) = x² + 1,5
c) f(x) = x² – 2,25
4. Mathematik-Nachhilfe-Aufgabe: Bestimme den Scheitelpunkt der Funktion.
Es ist die Funktion f(x) = (x – d)² gegeben. Es gilt bei der Funktion f(–1) = f(3). Ermittle für die Funktion deren Scheitelpunkt.

Lösungen zum Mathematik-Stoffgebiet quadratische Funktionen
1. Mathe-Nachhilfe-Aufgabe: Ermittle für die Funktion den Scheitelpunkt. Diese soll algebraisch mittels einer Termumformung bestimmt werden. Wie kann man von der Normalparabel ausgehend, den Scheitelpunkt in ein Koordinatensystem einzeichnen? Für welche x fällt der Graph der Funktion und für welche x steigt der Graph der Funktion?
a)
f(x) = x² – 2x – 6
x² – 2x – 6 = 0
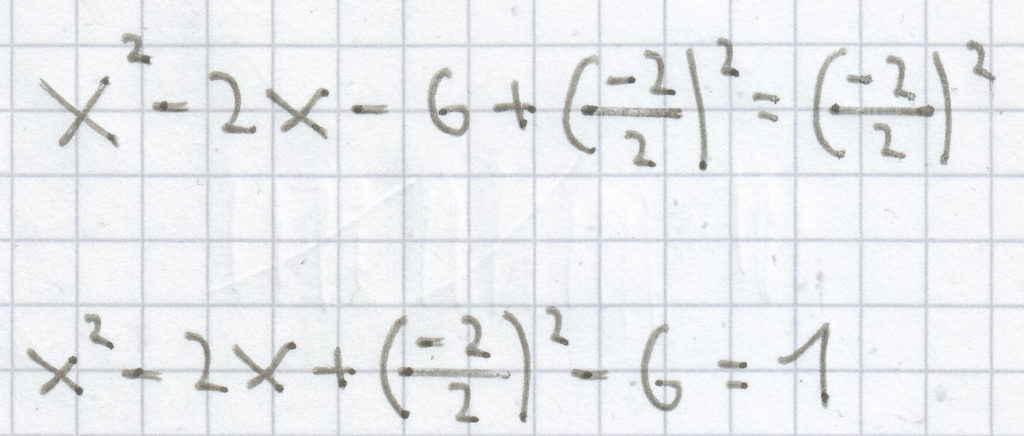
(x – 1)² – 6 = 1 | – 1
(x – 1)² – 7 = 0
f(x) = (x – 1)² – 7
S (1 | –7)
Von der Normalparabel ausgehend, die ja als Scheitelpunkt die Koordinaten S (0 | 0) hat, geht man entlang der x-Achse 1 Längeneinheit (LE) nach rechts und entlang der y-Achse sieben Längeneinheiten (LE) nach unten.
Die verschobene Normalparabel ist von links nach rechts innerhalb des Koordinatenysytems bis x = 1 fallend, danach steigend.
b)
f(x) = x² + 4x + 4
x² + 4x + 4 = 0
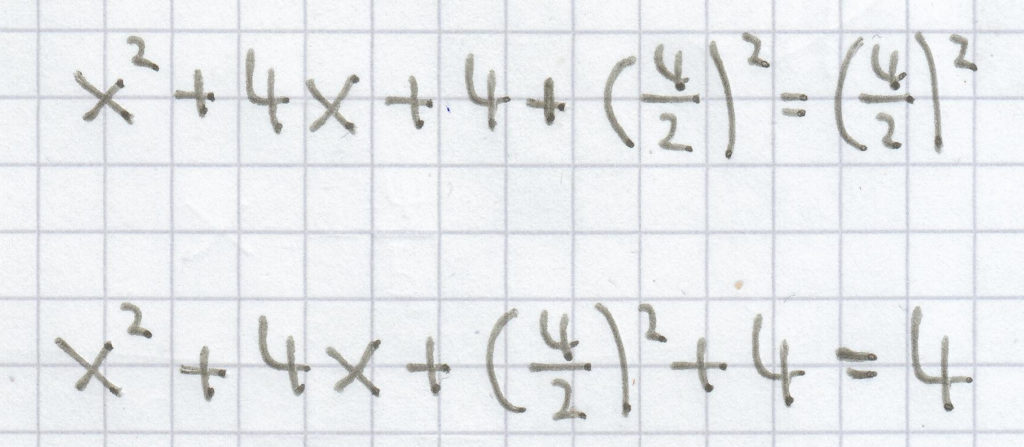
(x + 2)² + 4 = 4 | – 4
(x + 2)² = 0
f(x) = (x + 2)²
S (–2 | 0)
Ausgehend von der Nomalparabel muss man diese entlang der x-Achse um zwei Längeneinheiten nach links verschieben.
Die verschobene Normalparabel ist im Koordinatenystem von links nach rechts bis x = –2 fallend, darauf steigend.
c)
f(x) = x² – 6x
x² – 6x = 0
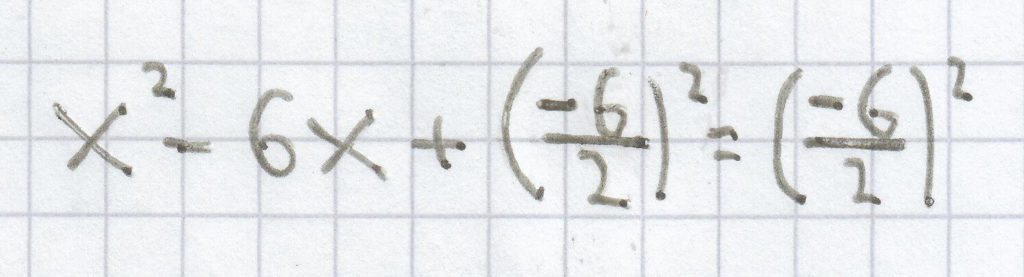
(x – 3)² = 9 | – 9
(x – 3)² – 9 = 0
f(x) = (x – 3)² – 9
S (3 | –9)
Ausgehnd von der Normalparabel geht man drei Längeneinheiten rechts entlang der x-Achse und neun Längeneinheiten nach unten entlang der y-Achse.
Von links nach rechts im Koordinatensystem ist die Funktion bis x = 3 fallend, danach ist die Funktion steigend.
d)
f(x) = x² + 8x + 3
x² + 8x + 3 = 0
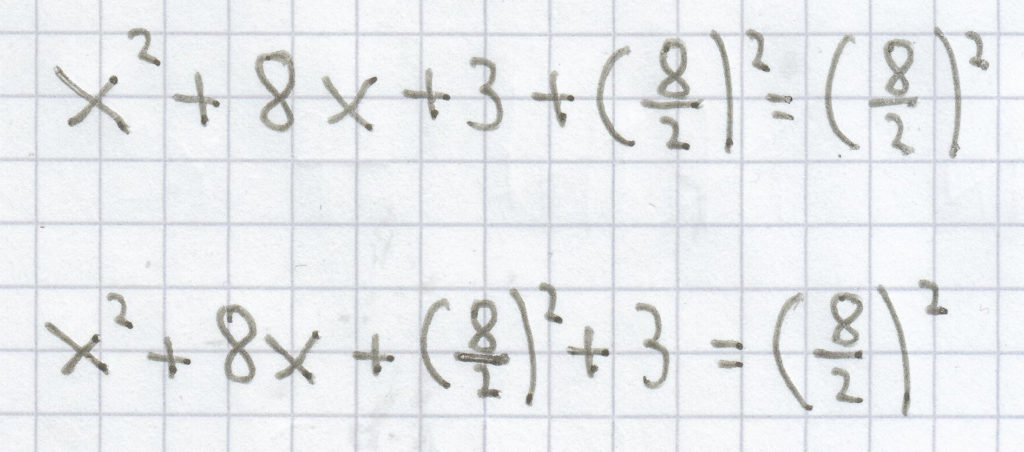
(x + 4)² + 3 = 16 | – 9
(x + 4)² – 13 = 0
f(x) = (x + 4)² – 13
S (–4 | –13)
Von der Normalparabel ausgehend, muss man diese zuerst vier Längeneinheiten nach links entlang der x-Achse verschieben und darauf dreizehn Längeneinheiten nach unten entlang der y-Achse verschieben.
Die quadratische Funktion ist von links nach rechts innerhalb des Koordinatensystems bix x = –4 fallend, danach ist sie steigend.
2. Mathematik-Nachhilfe-Aufgabe: Gib eine Gesetzmäßigkeiten mit eigenen Worten an, gib einen Termen für diese Gesetzmäßigkeit an.
a) Die Seitenlänge eines Quadrats wird verdoppelt. Wie groß ist nun der Flächeninhalt des Quadrats?
Der Flächeninhalt eine Quadrats bestimmt man wie folgt:
AQ = a · a
Die Seitenlänge wird nun verdoppelt:
AQ = 2a · 2a
AQ = 4a · a
Verdoppelt man die Seitenlänge eines Quadrats, dann vervierfacht sich der Flächeninhalt des Quadrats.
Beispiel: Ein Quadrat hat die Seitenlänge 3 cm.
AQ = 3 cm · 3 cm
AQ = 9 cm²
Die Seitenlänge wird verdoppelt:
AQ = 6 cm · 6 cm
AQ = 36 cm²
b) Der Flächeninhalt eines Quadrats soll doppelt so groß werden. Wie muss man die Seitenlängen des Quadrats verändern?
Der Flächeninhalt eines Quadrats berechnet man folgendermaßen:
AQ = a · a
Dadurch dass die Seitenlängen bei einem Quadrat gleich groß sind, verdoppelt sich der Flächeninhalt des Quadrats, wenn man jede Seitenlänge mit dem Faktor
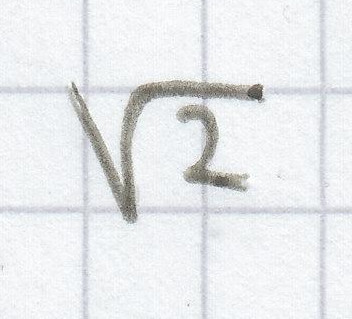
malnimmt. Denn es gilt ja:
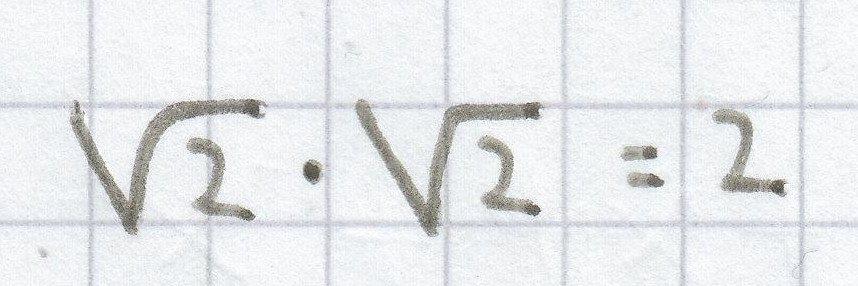
.
Der Flächeninhalt eines Quadrats verdoppelt sich, wenn man die Seitenlängen mit dem Faktor
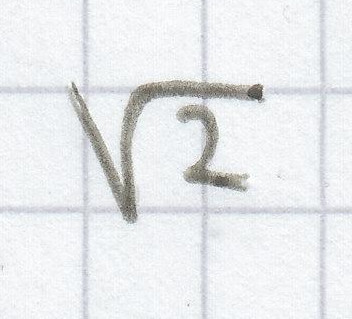
malnimmt.
AQ =
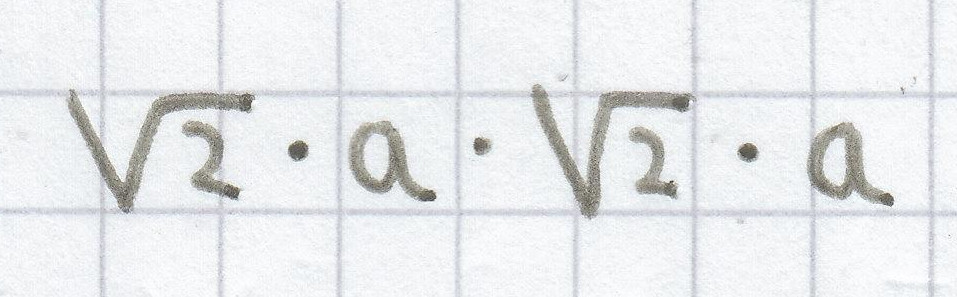
AQ = 2 · a · a
Beispiel: Ein Quadrat hat die Seitenlänge 10 cm. Sein Flächeninhalt ist:
AQ = 10 cm · 10 cm
AQ = 100 cm²
Der Flächeninhalt des Quadrats soll nun doppelt so groß sein, also 200 cm².
200 cm² = a · a
200 cm² = a² | √ a > 0
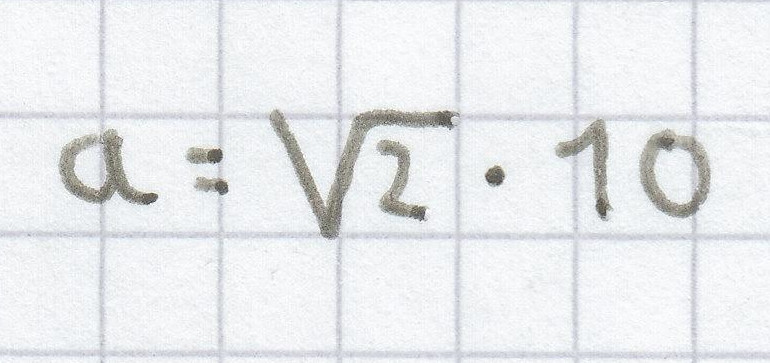
3. Mathematik-Nachhilfe-Aufgabe: Es soll der Graph der Funktion gezeichnet werden. Darüber hinaus soll der Scheitelpunkt sowie die Schnittpunkte mit den Koordninatenachsen ermittelt werden.
a) f(x) = x² – 2
Wie man hier sieht, handelt es sich um eine quadratische Funktion. Der Graph der Funktion ist die um 2 Längeneinheiten (LE) entlang der y-Achse verschobene Normalparabel.
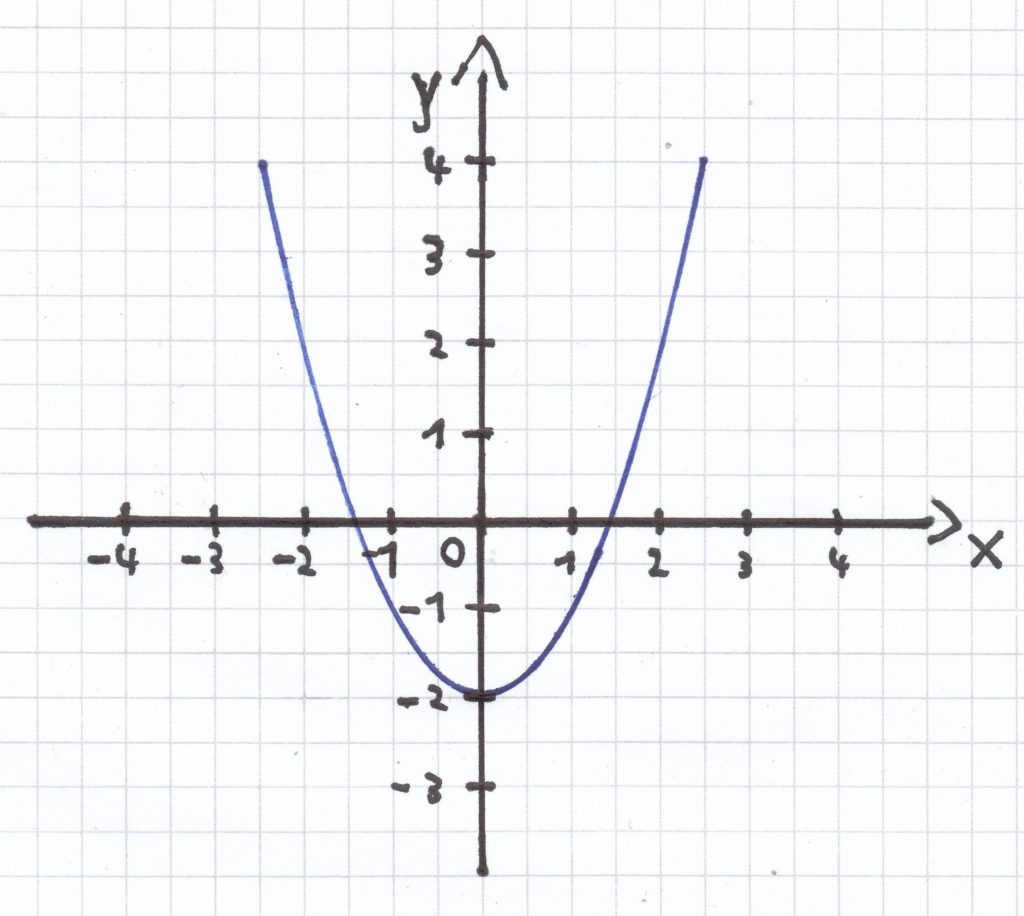
Der Scheitelpunkt der Funktion ist daher S (0 | –2).
Ein Schnittpunkt mit der x-Achse ist ungefähr bei P1 (1,4 | 0), der andere Schnittpunkt mit der x-Achse ist etwa bei P2 (–1,4 | 0).
Der Schnittpunkt mit der y-Achse ist: P (0 | –2).
b) f(x) = x² + 1,5
Hier ist die Normalparabel um 1,5 LE nach oben, entlang der y-Achse verschoben. Aufgabe
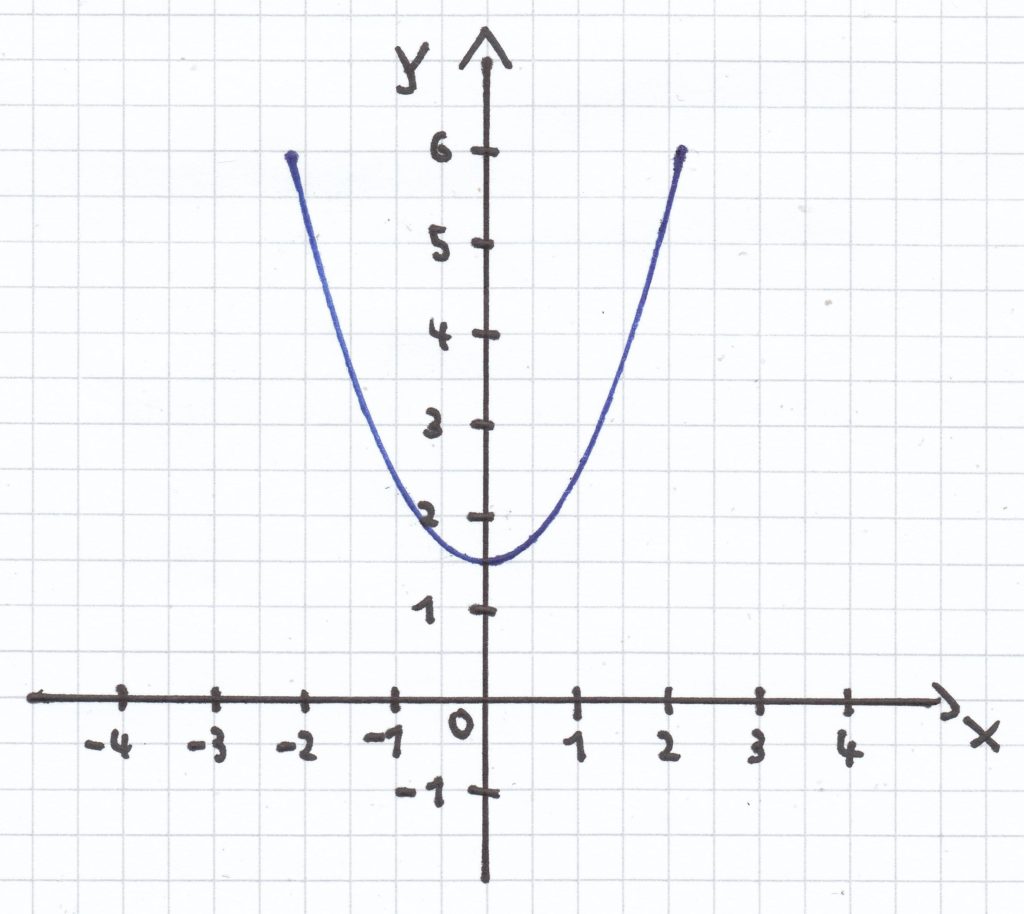
Der Scheitelpunkt der Funktion ist: S (0 | 1,5).
Der Schmittpunkt mit der y-Achse ist identisch mit dem Scheitelpunkt: P (0 | 1,5).
Die Funktion besitzt keinen Schnittpunkt mit der x-Achse.
c) f(x) = x² – 2,25
Hier ist die Normalparabel um 2,25 LE nach unten, entlang der y-Achse verschoben.
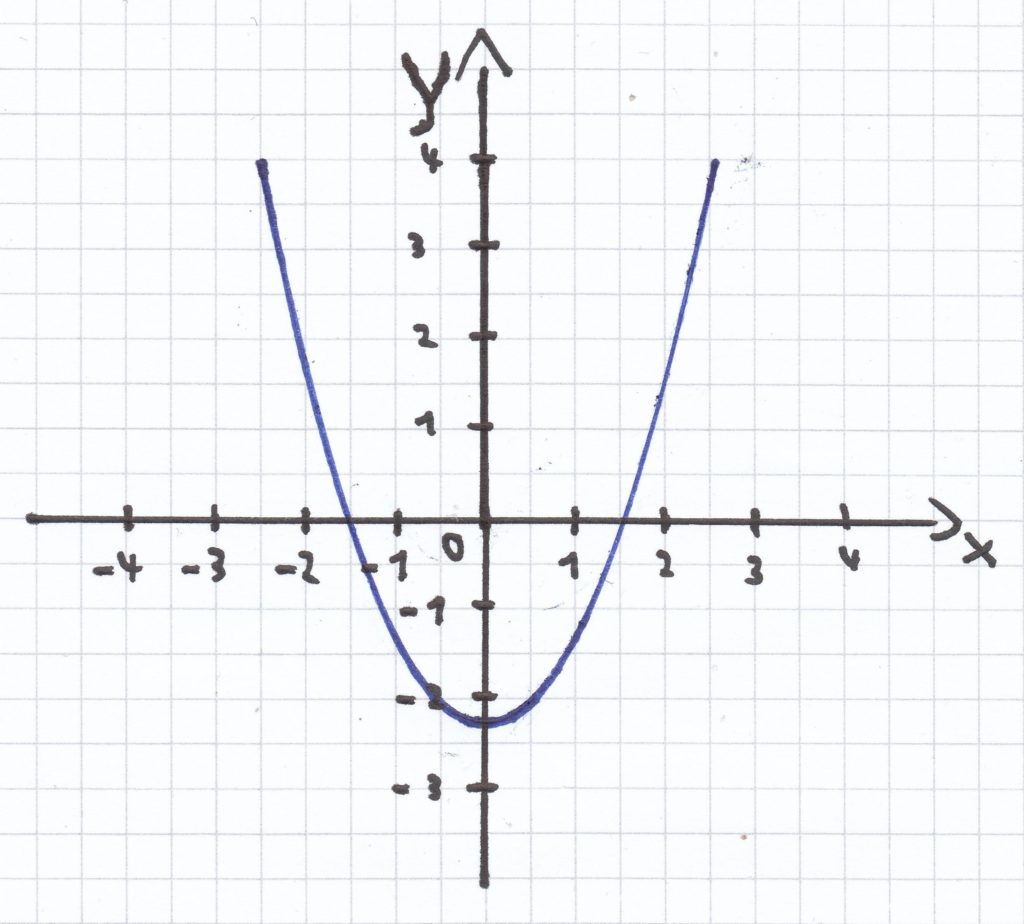
Der Scheitlpunkt der Funktion ist: S (0 | –2,25).
Der eine Schnittpunkt mit der x-Achse ist: P1 (–1,5 | 0), der andere Schnittpunkt mit der x-Achse ist: P2 (1,5 | 0).
Der Schnittpunkt mit der y-Achse ist: P (0 | –2,25).
4. Mathe-Nachhilfe-Aufgabe: Ermittle den Scheitelpunkt der Funktion.
Gegeben ist die Funktion: f(x) = (x – d)² . Es gilt: Bei der Funktion ist f(–1) = f(3). Bestimme für die Funktion deren Scheitelpunkt.
An der Stelle x = –1 und an der Stelle x = 3 hat die Funktion den gleichen y-Wert.
Deshalb gilt:
(–1 – d)² = (3 – d)²
Diese Gleichung muss man nun nach der Variablen d hin auflösen.
(1 + d)² = (3 – d)²
Hier liegt die 1. Binomische Formel vor sowie die 2. Binomische Formel.
(1 + d)² = (3 – d)²
(1)² + 2 · 1 · d + (d)² = (3)² – 2 · 3 · d + (d)²
1 + 2d + d² = 9 – 6d + d² | – d²
1 + 2d = 9 – 6d | + 6d
1 + 8d = 9 | – 1
8d = 8 | : 8
d = 1
Die Funktion ist: f(x) = (x – 1)².
Der Scheitelpunkt der Funktion ist: S (1 | 0).