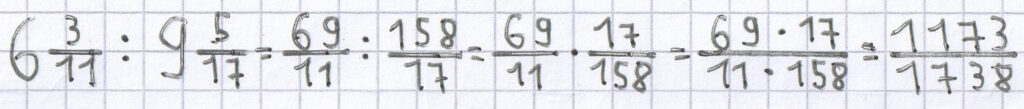1. Allgemeines zur Multiplikation und Division von Brüchen
Für die Multiplikation und Division von Bruchzahlen gilt genauso wie bei der Addition und Subtraktion von Brüchen, dass sich die bei den Grundrechenarten erworbenen Fähigkeiten hier entschieden auszahlen. Hierbei profitiert man bei der Multiplikation und Division von Brüchen vor allem, wenn man in Mathe folgende Rechenoperation besonders gut verinnerlicht hat: das Multiplizieren. Ja, man hat hier richtig gelesen: nur das Multiplizieren! Das stellt nämlich eine Besonderheit beim Bruchrechnen dar. Denn sowohl die Multiplikation als auch die Division von Brüchen erfolgt über ein Multiplizieren. Da es sich hierbei, bei dem Multiplizieren und dem Dividieren von Brüchen, aber dennoch um zwei unterschiedliche Rechenoperationen handelt, erfolgt die Berechnung logischerweise auf unterschiedliche Weise. Das ist ja irgendwie auch klar, da ja ansonsten die Multiplikation und die Division von Brüchen haargenau gleich wären. Dieses widerspricht natürlich aber fundamental jeder Mathe-Logik.
2. Die Multiplikation von Brüchen
Für die Multiplikation von Brüchen in Mathe gilt: Sowohl echte als auch unechte Brüche werden dahingehend multipliziert, indem man stets Zähler mal Zähler malnimmt und Nenner mal Nenner malnimmt.
Bei der Multiplikation von gemischten Brüchen gilt: Jeder gemischte Bruch, der mit einem anderen Bruch malgenommen wird, muss vorher in einen unechten Bruch umgewandelt werden. Darauf dürfen wiederum sämtliche Zähler miteinander malgenommen werden und sämtliche Nenner.
2.1 Die Multiplikation von echten und unechten Brüchen
Bei einer Multiplikation von echten und unechten Brüchen wird sowohl jeder Zähler als auch jeder Nenner miteinander malgenommen.
Beispiele für die Multiplikation von echten Brüchen:

Zum Kürzen von Brüchen siehe auch unter Bruchrechnung/Erweitern und Kürzen das Kapitel 3. Das Kürzen eines Bruchs an.

;
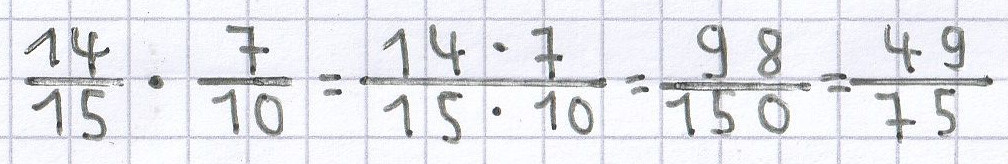
Die Multiplikation dieser beiden Brüche hätte man auch folgendermaßen machen können:
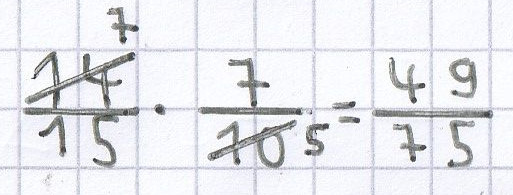
Findet man bei einer Multiplikation bei beiden Brüchen zwischen Zähler und Nenner einen gemeinsamen Teiler, so kann man diese beiden Brüche „über Kreuz“ mit dem gemeinsamen Teiler kürzen. Als Hochzahl schreibt man bei dem gekürzten Zähler und Nenner jeweils den Wert hin, der nach dem Kürzen übrig bleibt. Übersieht man jedoch, dass man „über Kreuz“ kürzen kann, dann kann man das wie oben bei der Aufgabe immer noch machen, wenn man die Multiplikation der Brüche durchgeführt hat.
Beispiele für die Multiplikation von unechten Brüchen:
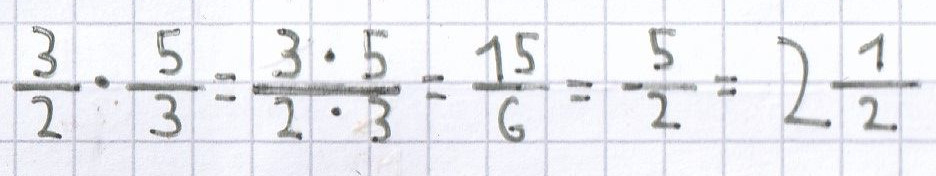
Zum Umwandeln von unechten Brüchen in gemischte Brüche siehe auch unter Bruchrechnung das Kapitel 4.1 Das Umrechnen eines unechten Bruchs in eine gemischten Bruch an.
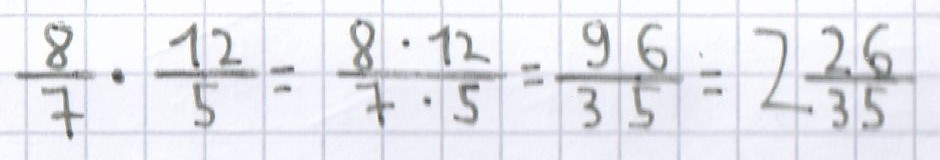
;
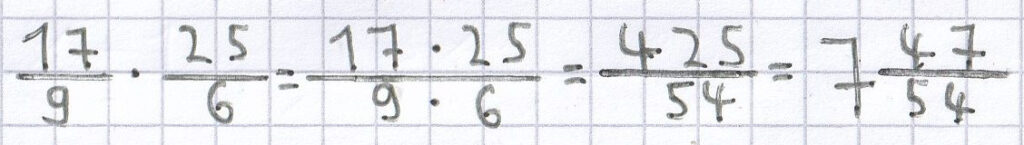
2.2 Die Multiplikation von gemischten Brüchen
Bevor man gemischte Brüche malnehmen darf, muss man diese immer zuvor in unechte Brüche umwandeln. Anschließend darf man Zähler und Zähler und Nenner Nenner miteinander malnehmen.
Beispiele für die Multiplikation von gemischten Brüchen:
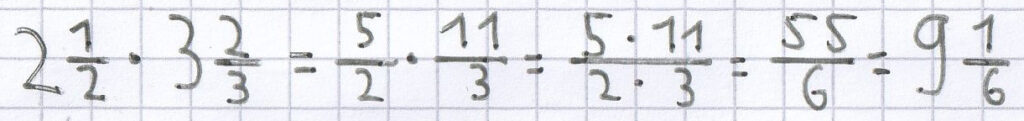
;
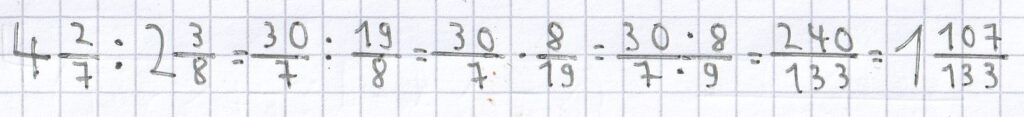
;
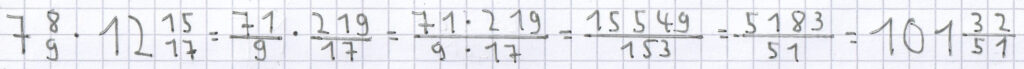
3. Die Division von Brüchen
Ein Division bei Brüchen stellt immer eine Multiplikation dar. Das klingt widersprüchlich, ist es aber nicht. Denn ein Bruch wird durch einen anderen Bruch dividiert, indem man bei dem zweiten Bruch den Kehrwert bildet und anschließend beide Brüche miteinander multipliziert. Der Kehrwert eines Bruches ist hierbei einfach das Vertauschen des Nenners und des Zählers.
3.1 Die Division von echten und unechten Brüchen
In Mathe bei der Bruchrechnung darf man nach der Bildung des Kehrwerts sofort sowohl echte als auch unechte Brüche miteinander malnehmen.
Beispiele für die Division von echten Brüchen:
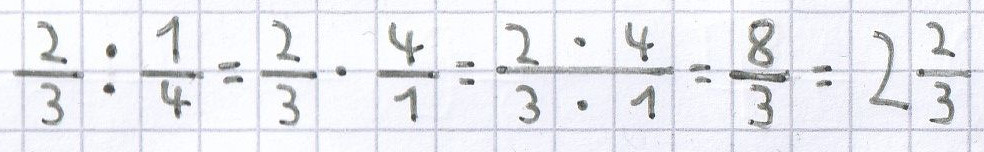
;
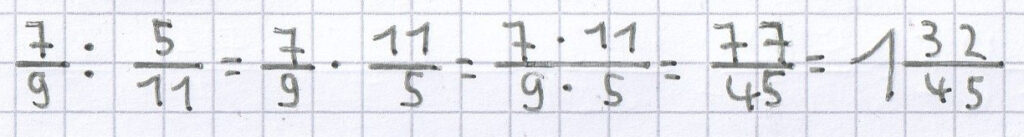
;
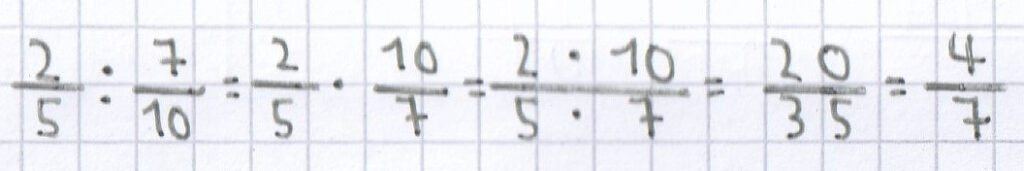
Hat man den Kehrwert bei der Division von Brüchen gebildet und „über Kreuz“ findet man bei den beiden Brüche zwischen Zähler und Nenner einen gemeinsamen Teiler, so kann man diese jeweils mit dem gemeinsamen Teiler kürzen. Als Hochzahl schreibt man über den gekürzten Zähler und Nenner den Wert, der nach dem Kürzen übrig bleibt.
Beispiele für die Division von unechten Brüchen:

;
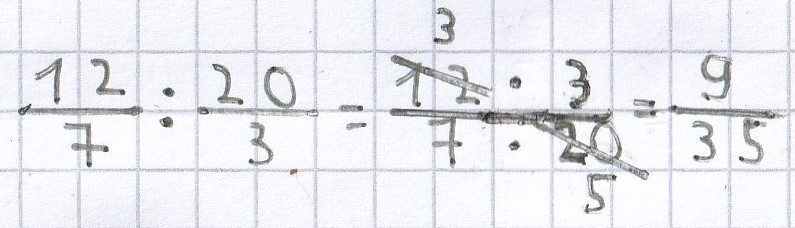
;
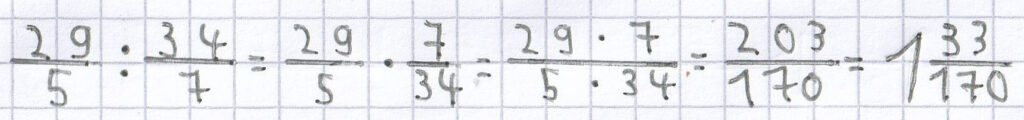
3.2 Die Division von gemischten Brüchen
Bei der Division von gemischten Brüchen gilt das Gleiche wie bei der Multiplikation von gemischten Brüchen: Bevor man die Rechenoperation durchführen darf, müssen diese immer vorher in unechte Brüche umgewandelt werden.
Beispiele für die Division von gemischten Brüchen:
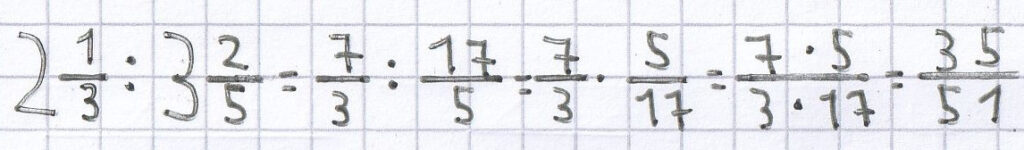
;
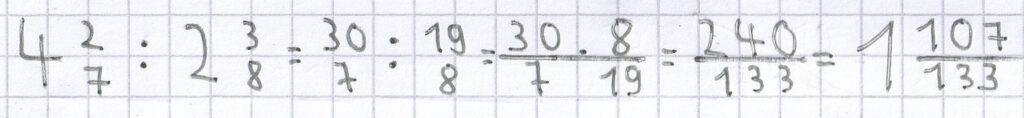
;