1. Allgemeines zu linearen Funktionen
Die ersten Funktionen, die im Fach Mathe behandelt werden, sind lineare Funktionen. Da Funktionen ein sehr wichtiges Mathematik-Stoffgebiet darstellen, sollte man hier besonders gut aufpassen, um zu verstehen, was Funktionen sind. Dann wird man sich bei allen noch kommenden Funktionen sowie der Analysis, bei der umfangreiche Funktionsuntersuchungen gemacht werden, umso leichter tun.
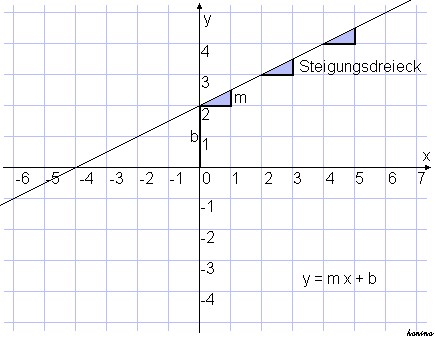
Der namensgebende Teil von linearen Funktionen, das „Linear“, ist aus dem Lateinischen und bedeutet „linienförmig, geradlinig“. Wenn man lineare Funktionen in ein Koordinatensystem einzeichnet, sieht man sofort, dass ihr Graph „linienförmig, geradlinig“ verläuft – und versteht, warum diese Funktionen „lineare Funktionen“ heißen.
Die Wertetabelle, der hier dargestellten linearen Funktion
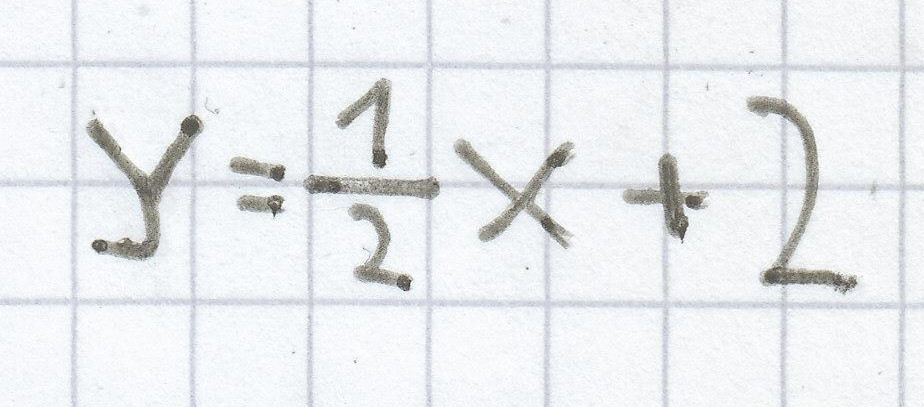
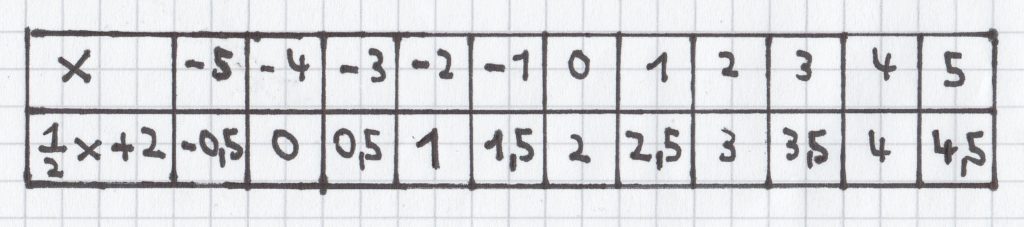
2. Charakteristika linearer Funktionen
Lineare Funktionen können immer allgemein mithilfe dieser Zuordnungsvorschrift beschrieben werden:
x ↦ m · x + n
(Zuordnungsvorschrift einer linearen Funktion)
oder mittels folgender Funktionsgleichung:
y = m · x + n.
Die Definitionsmenge ist ℚ.
Das m bei der Zuordnungsvorschrift oder der Funktionsgleichung ist die Steigung und zeigt immer auf, was für eine Steigung (ob positiv oder negativ und ob steil oder eher flach) die lineare Funktion besitzt; das n bei der Zuordnungsvorschrift oder Funktionsgleichung ist das absolute Glied bzw. der Ordinatenabschnitt (das ist der Schnittpunkt mit der y-Achse im Koordinatensystem). Durch das absolute Glied zeigt sich jeweils, an welcher Stelle die lineare Funktion im Koordinatensystem die y-Achse schneidet.
Der Graph einer linearen Funktion ist immer eine Gerade bzw. geradlinig. Der Schnittpunkt zwischen linearer Funktion und der y-Achse weist hierbei stets die Koordinaten P (0 | n) auf.
Eine lineare Funktion muss nicht immer eine Steigung vorweisen, da m auch = 0 sein kann. Ist m = 0, so verläuft der Graph der linearen Funktion immer parallel zur x-Achse.
Ebenso muss eine lineare Funktion kein absolutes Glied besitzen. Ist nämlich n = 0 so schneidet die lineare Funktion die y-Achse immer bei 0 und weist dann die Koordinate P (0 | 0) auf. Man sagt dann, der Graph ist eine Ursprungsgerade, da die Gerade immer durch den Anfang/Ursprung des Koordinatensystems geht.
Je nach Vorzeichen von m ist eine Gerade (streng monoton) steigend oder (streng monoton) fallend. Ist nämlich m positiv/„+“ so sagt man, dass die Gerade eine positive Steigung hat, ist hingegen m negativ/„–“ so sagt man, dass die Gerade eine negative Steigung besitzt.
Abhängig von Größe der Zahl, die die Steigung wiedergibt, kann man sagen, ob die lineare Funktion „steil“ oder „flach“ verläuft. Je größer nämlich die Steigung m ist, desto steiler (streng monoton steigend/fallend) verläuft die linearer Funktion. Je kleiner demzufolge die Steigung m ist, desto flacher (streng monoton steigend/fallend) verläuft die lineare Funktion.
Als Orientierung ist hierbei hilfreich:
Ist die Steigung m > 1, umso steiler steigt sie an. Ist die Steigung m < 1 desto flacher steigt sie an.
ist die Steigung m < –1, desto steiler fällt sie. Ist die Steigung m > –1 desto flacher fällt sie.
3. Ermittlung der Steigung und des Schnittpunktes mit der y-Achse anhand der Funktionsgleichung
Beispiele:
Folgendes sind alles lineare Funktionen. Bestimme ihre Steigung und der Schnittpunkt mit der y-Achse, gebe weiter an, ob die Funktion ansteigt oder fällt.
a) y = 2x + 5
b) y = –3 · x + 3
c)
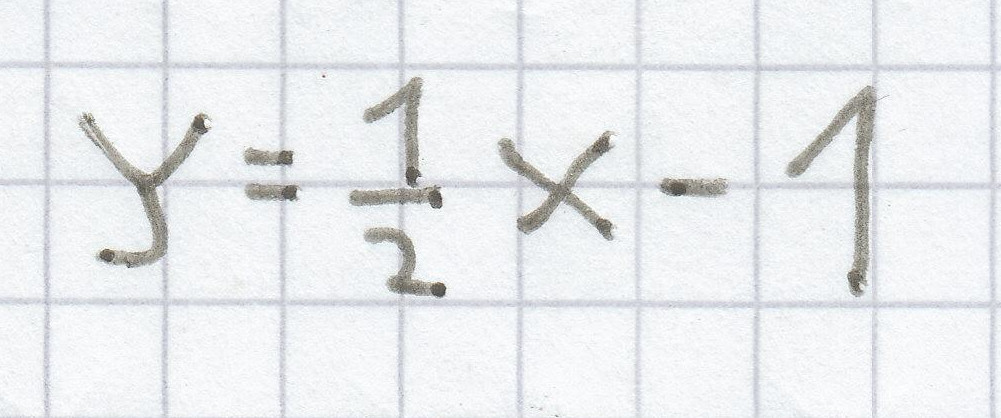
d) y = –0,25 · x + 6
e) y = x – 3
f) y = 2x
g) y = 3
Ist die Funktionsgleichung einer linearen Funktion gegeben, so kann man hiervon immer sofort die Steigung m und das absolute Glied n ermitteln.
Die Steigung m steht bei einer linearen Funktion immer vor der Variablen und stellt hierbei einen Faktor dar. Daher ist die Steigung m mit der Variablen mittels einer Multiplikation verbunden. Das absolute Glied n schließt sich an die Steigung mittels einer Addition oder Subtraktion an.
a) y = 2x + 5
Hier ist die Steigung m = 2 und das absolute Glied n = 5. Da die lineare Funktion eine positive Steigung besitzt, steigt sie. Die y-Achse schneidet sie im Punkt P (0 | 5).
b) y = –3 · x + 3
Bei dieser linearen Funktion ist die Steigung m = –3 und das absolute Glied n = 3. Da hier die Steigung ein Minus vorweist, ist diese fallend. Im Punkt P (0 | 3) wird die y-Achse geschnitten.
c)
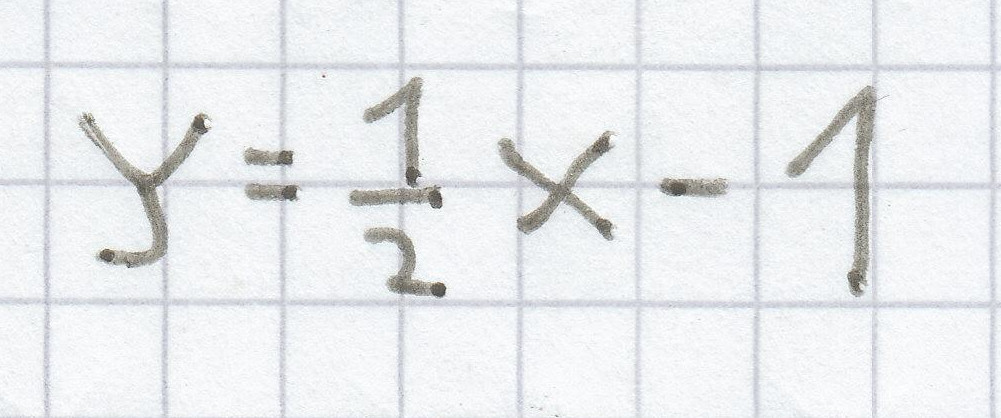
Hier ist die Steigung m =
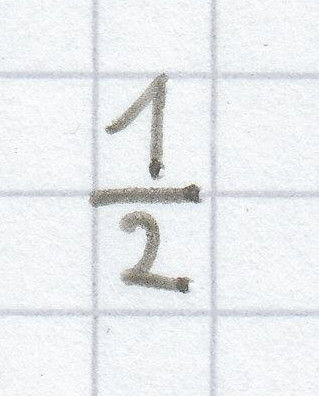
und das absolute Glied n = –1. Da die Steigung positiv ist, steigt die Funktion, aber sie verläuft nicht allzu steil. Denn die Steigung m ist < 1. Der Schnittpunkt mit der y-Achse ist P (0 | –1).
d) y = –0,25 · x + 6
Diese lineare Funktion besitzt die Steigung m = –0,25 und als absolutes Glied n = 6. Da m negativ ist, ist die Funktion fallend und da m < 1 eher leicht fallend. Bei P (0 | 6) schneidet die lineare Funktion die y-Achse.
e) y = x – 3
Steht keine Zahl vor der Variablen so, ist die Steigung m immer = 1. Denn die Funktionsgleichung ist dann nichts anderes als y = 1 · x – 3. Das absolute Glied n = – 3. Da die Steigung m positiv ist, steigt die lineare Funktion. Die Funktion schneidet die y-Achse in dem Punkt P (0 | –3).
Steht bei der Funktionsgleichung einer linearen Funktion vor der Variablen nur ein Minus und kein weitere Faktor, so ist die Steigung immer m = –1.
f) y = 2x
Bei dieser linearen Funktion ist die Steigung m = 2. Da dahinter keine Zahl steht, ist das absolute Glied n = 0. Die Funktion ist steigend, da m positiv ist. Aufgrund der Steigung m > 1 steigt diese steil an. Der Schnittpunkt mit der y-Achse ist bei P (0 | 0). Hier handelt es sich also um eine Ursprungsgerade, da die lineare Funktion durch den Koordinatenurspung geht.
g) y = 3
Da diese Funktion keine Variable vorweist, hat sie auch keine Steigung. Die Steigung m ist demzufolge = 0. Das absolute Glied ist n = 3. Eine lineare Funktion, die keine Steigung besitzt, verläuft immer parallel zur x-Achse. Den Schnittpunkt mit der y-Achse hat die Funktion bei P (0 | 3).
4. Bestimmung der Funktionsgleichung vom Graphen der linearen Funktion
Anhand einer gegebenen Funktionsgleichung kann man immer die Steigung und deren Schnittpunkt mit der y-Achse ermitteln. Mittels des Graphen einer linearen Funktion, der immer eine Gerade darstellt, kann man umgekehrt immer die Funktionsgleichung aufstellen. Hierfür muss zum einen die Steigung und zum anderen das absolute Glied ermittelt werden.
4.1 Bei positiver Steigung
- Das Ermitteln der Steigung m
Um die Steigung einer linearen Funktion zu ermitteln, bedient man sich eines sogenannten Steigungsdreiecks. Bei dem unten darstellten Graphen einer linearen Funktion sind zwei Steigungsdreiecke mit der Farbe grün eingezeichnet worden. Wie man sieht, weist jedes Steigungsdreieck einen x-Wert und einen y-Wert auf. Damit man den jeweiligen x-Wert und den jeweiligen y-Wert des Steigungsdreiecks genau ermitteln kann, muss man das Steigungssdreieck möglichst immer entlang ganzer Karos einzeichnen. Zudem ist es wichtig, möglichst das Steigungsdreieck immer gleich in den Graphen der linearen Funktion einzuzeichnen. Bei einer linearen Funktion mit positiver Steigung ist es am einfachsten, immer den x-Wert des Steigungsdreiecks nach rechts einzuzeichnen (das steht dann für einen positiven Zahlenwert) und der y-Wert nach oben hin (das steht dann ebenso immer für einen positiven Zahlenwert). Hierbei ist es egal, wie groß das Steigungsdreieck ist, entscheidend ist nur, dass es möglichst entlang ganzer Karos geht, um exakte Zahlenverhältnisse herauslesen zu können. Denn anschließend ermittelt man die Steigung m, indem man folgenden Quotienten des Steigungsdreiecks bildet:
m =

Fährt man gedanklich das Steigungsdreieck von der x-Achse beginnend und der Geraden hin zu y Achse und wiederum zur Geraden, so hat man auch der Reihe nach immer alle zu ermittelnden Werte: x1 zu Beginn, beim Übergang hin zu Vertikalen x2, dort ist auch y1. Am Ende des Steigungsdreiecks ist schließlich y2.
Bei dem unteren Graphen hat das eine Steigungsdreieck den x-Wert 1 (x2 = 1, x1= 0; x2 – x1 = 1 – 0 = 1) und den y-Wert 2 (y2 = 4, y1 = 2; y2 – y1= 4 – 2 = 2); das andere Steigungsdreieck hat den x-Wert 2 (x2 = –0,5, x1= –2,5; x2 – x1 = –0,5 – (–2,5) = 2) und den y-Wert 4 (y2 = 1, y1 = –3; y2 – y1 = 1 – (–3) = 4).
Demzufolge ergibt sich für diese lineare Funktion folgende Steigung:
m =
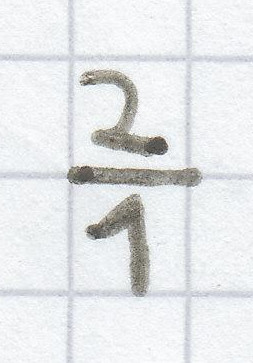
= 2
oder:
m =
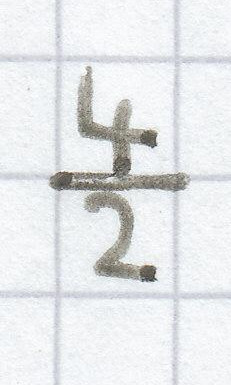
= 2
- Das Ermitteln des absoluten Gliedes n
Das absolute Glied einer linearen Funktion kann man immer aus dem Schnittpunkt mit der y-Achse herauslesen. Denn hier gilt P (0 | n). Da hier P (0 | 2) ist, ist n = 2.
- Das Aufstellen der Funktionsgleichung:
Die Funktionsgleichung einer linearen Funktion lautet: y = mx + n. Jetzt muss man nur noch die ermittelten Werte, die Steigung m und das absolute Glied n, in die Funktionsgleichung einsetzen: y = 2x + 2
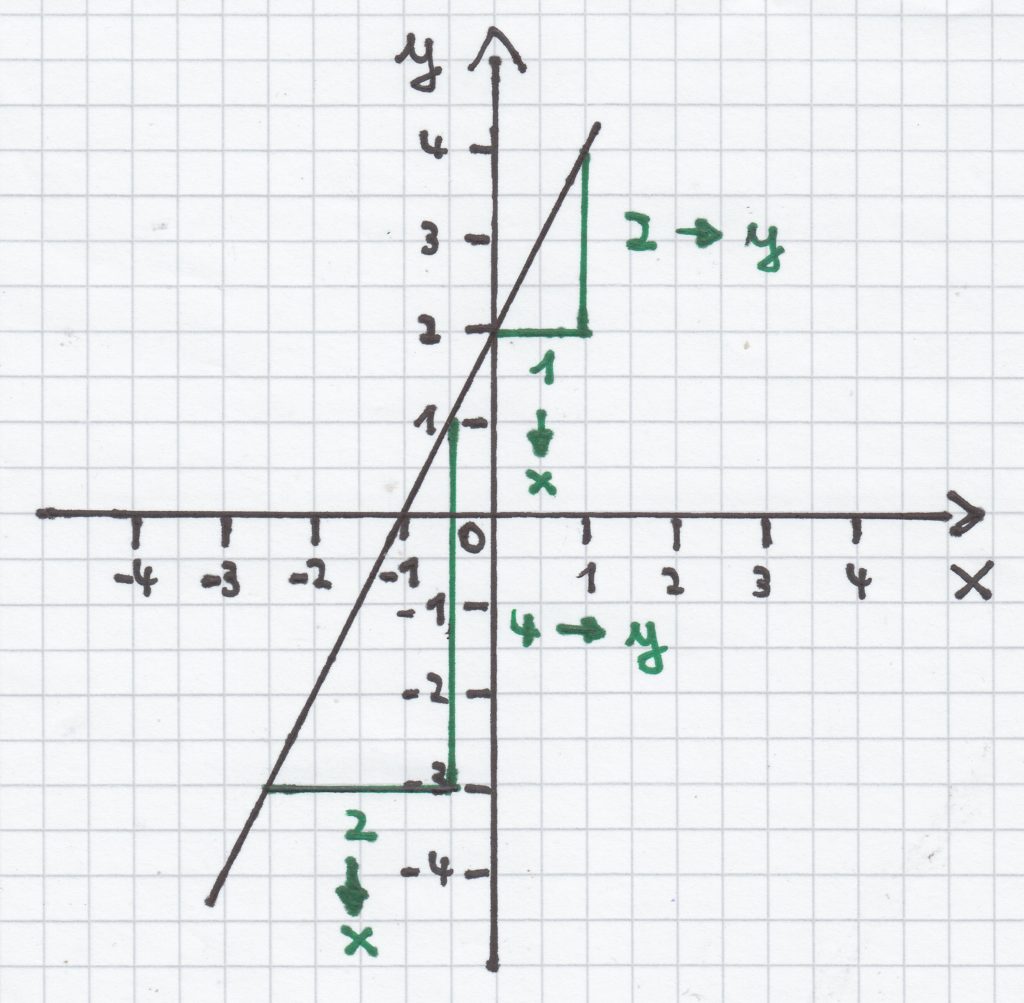
4.2 Bei negativer Steigung
- Das Ermitteln der Steigung m
Hier fährt man wiederum am besten gedanklich das Steigungsdreieck ab, beginnend von der Geraden entlang der x-Achse, hier ist x1, der Übergang zur Vertikalen ist x2. Dort ist auch y1. Am Ende des Steigungsdreiecks hin zur Geraden befindet sich schließlich y2.
Bei dem unteren Graphen hat das Steigungsdreieck den x-Wert –2 ( x2 = –4, x1= –2; x2 – x1 = –4 – (–2) = –2) und den y-Wert 1 (y2 = 1, y1 = 0; y2 – y1 = 1 – 0 = 1); das andere Steigungsdreieck hat x-Wert –4 (x2 = –1, x1 = 3; x2 – x1 = –1 –3 = –4) und den y-Wert 2 (y2 = –0,5, y1 = –2,5; y2 – y1 = –0,5 – (–2,5= 0 2).
Deshalb ergibt sich für diese lineare Funktion folgende Steigung:
m =
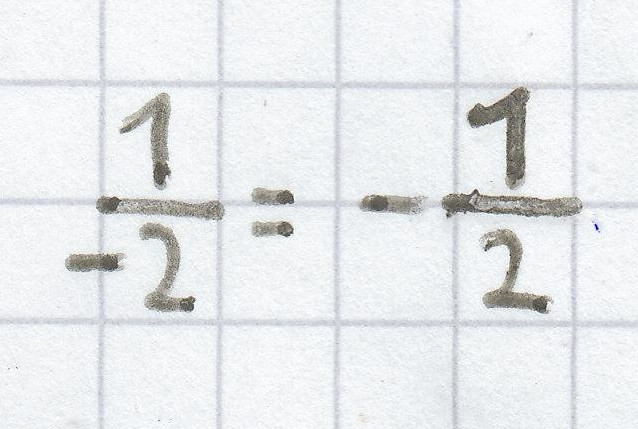
oder: m =
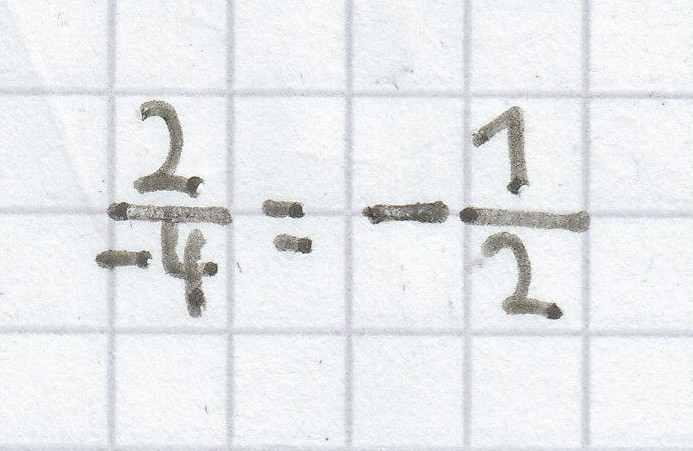
- Das Ermitteln des absoluten Gliedes n
Das absolute Glied kann man immer aus dem Schnittpunkt mit der y-Achse herauslesen. Diese ist hier P (0 | –1). Daher ist hier n = –1.
- Das Aufstellen der Funktionsgleichung
Die Funktionsgleichung einer linearen Funktion ist immer f(x) = mx + n. Demzufolge ergibt sich nach dem Einsetzen der ermittelnden Werte folgende Funktionsgleichung für diese linearen Funktion hier:
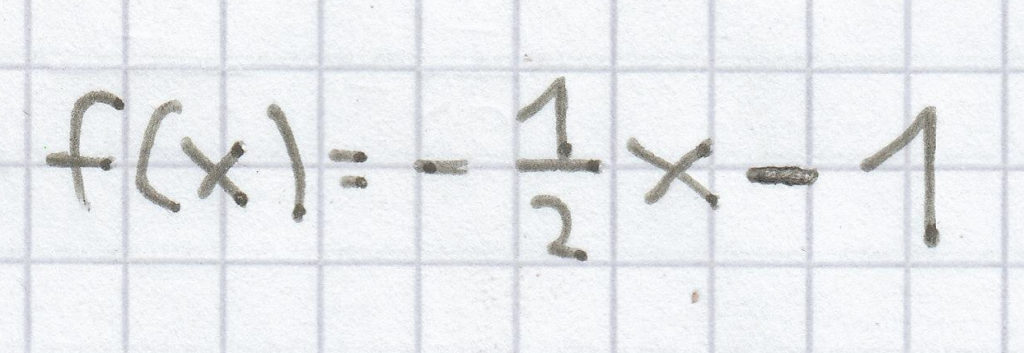
5. Das Zeichnen von linearen Funktionen
Der Graph einer linearen Funktion ist immer eine Gerade. Daher benötigt man zum Zeichnen einer linearen Funktion immer auch nur zwei Punkte. Diese zwei Punkte ermittelt man am einfachsten aus der gegeben Funktionsgleichung. Ein Punkt ist hierbei stets der Schnittpunkt mit der y-Achse, der Punkt P (0 | n). Der andere Punkt ergibt sich nun, indem man ein Steigungsdreieck von dem Schnittpunkt mit der y-Achse aus bildet.
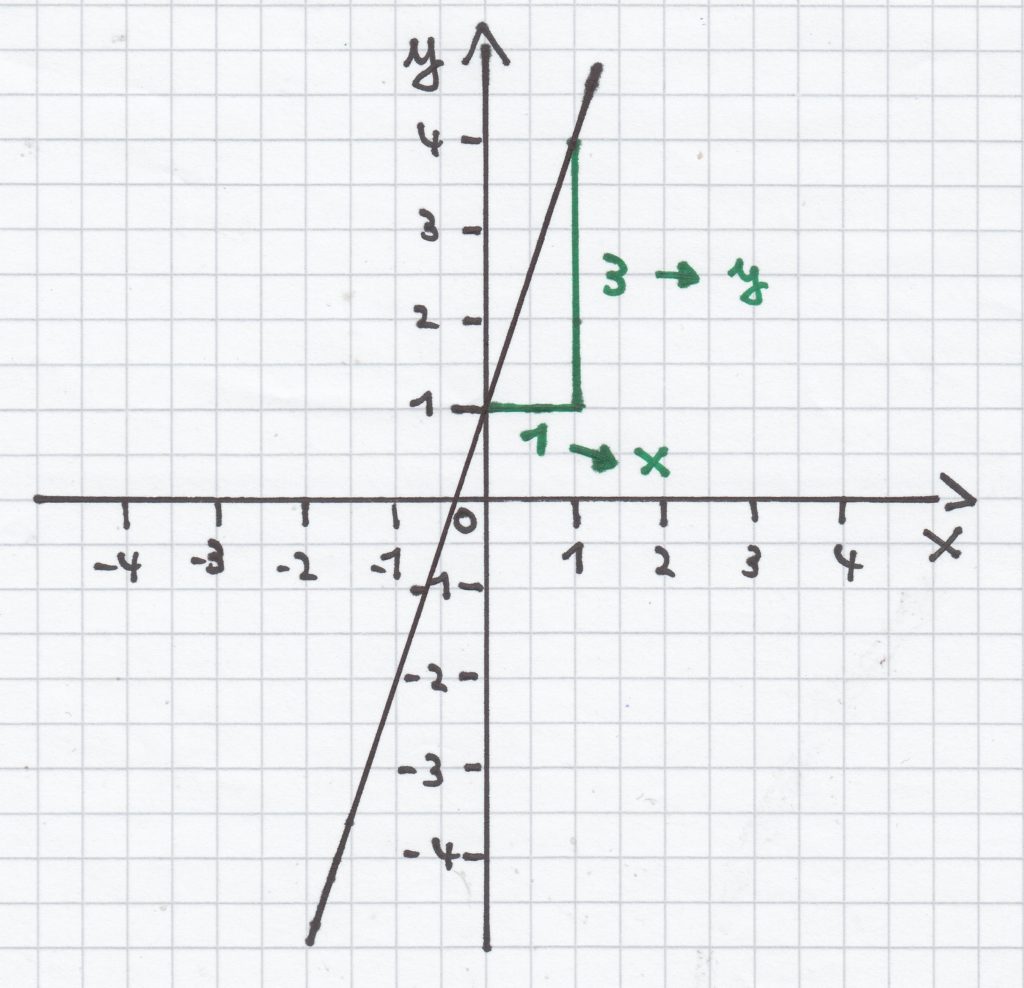
5.1 Das Zeichnen einer linearen Funktion mit positiver Steigung
Es ist folgende Funktionsgleichung einer linearen Funktion gegeben:
y = 3x + 1
Den Schnittpunkt mit der y-Achse kann man hierbei sofort herauslesen. Dieser ist P (0 | 1), ebenso die Steiung, die hier m = 3
bzw.
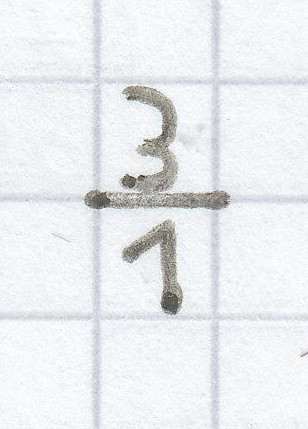
ist.
Ist nun die Steigung m jeweils eine ganzzahlige Zahl, so bildet man hieraus jeweils eine Bruchzahl.
Nach dem Ermitteln der Steigung kann man das Steigungsdreieck an den Schnittpunkt mit der y-Achse bilden. Hierbei geht man eine Längeneinheit/LE nach rechts und 3 Längeneinheiten/LE nach oben, da ja hier eine positive Steigung vorliegt. Darauf kann man die Gerade der linearen Funktion zeichnen.
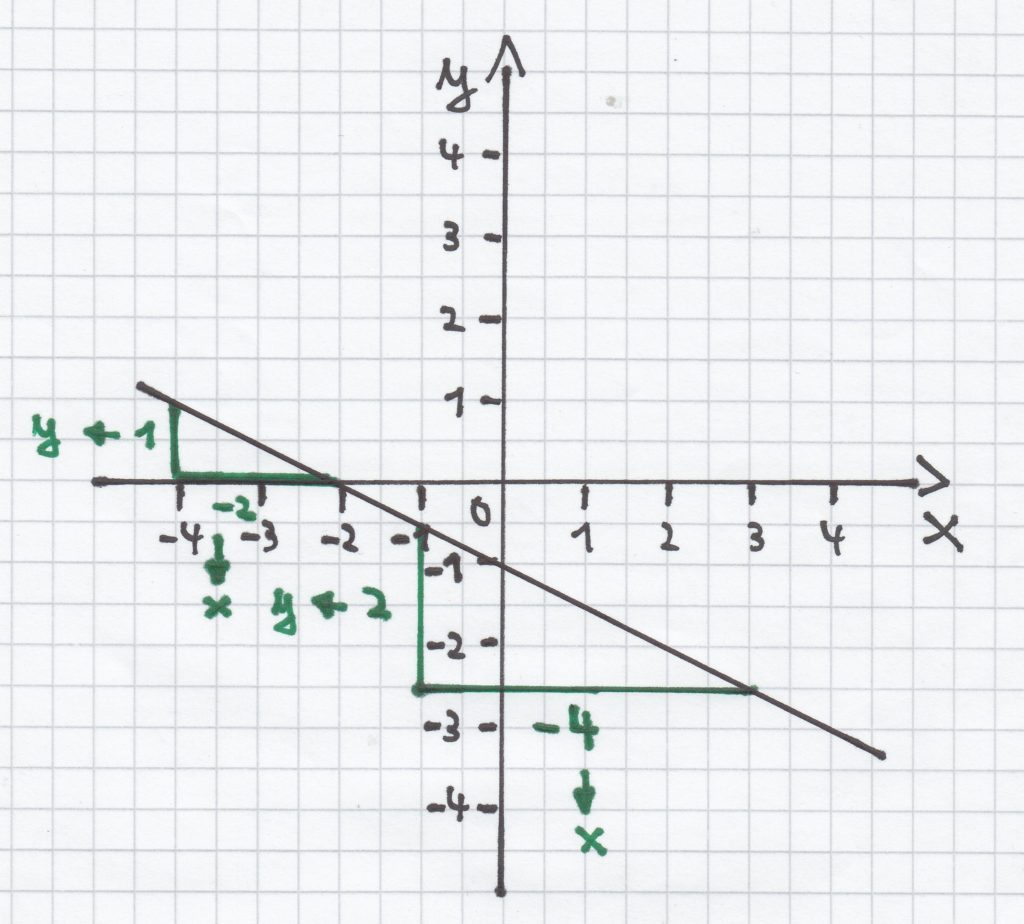
5.2 Das Zeichnen einer linearen Funktion mit negativer Steigung
Folgende Funktionsgleichung einer linearen Funktion ist gegeben:
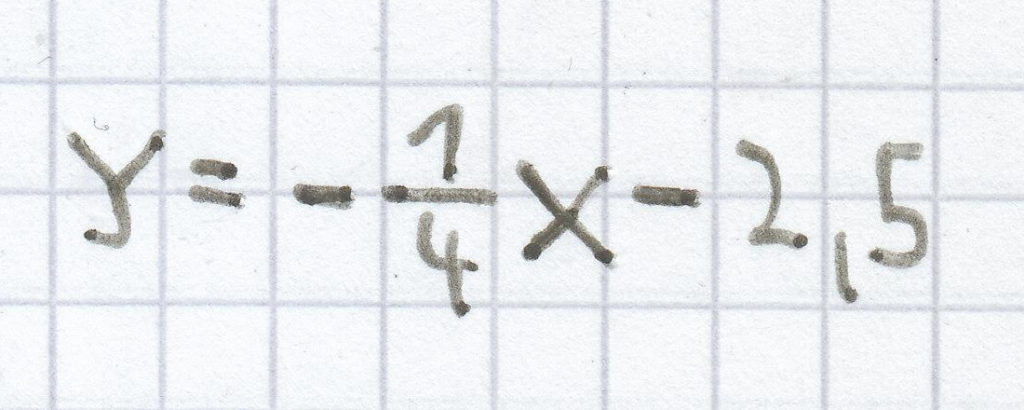
Der Schnittpunkt mit der y-Achse ist hier P (0 | −2,5), die Steigung m ist

.
Vom Schnittpunkt mit der y-Achse ausgehend kann man nun das Steigungsdreieck einzeichnen. Hierbei geht man vier Längeneinheiten/LE nach links, da eine negative Steigung vorliegt, und eine Längeneinheit/LE nach oben. Darauf kann man die Gerade zeichnen.
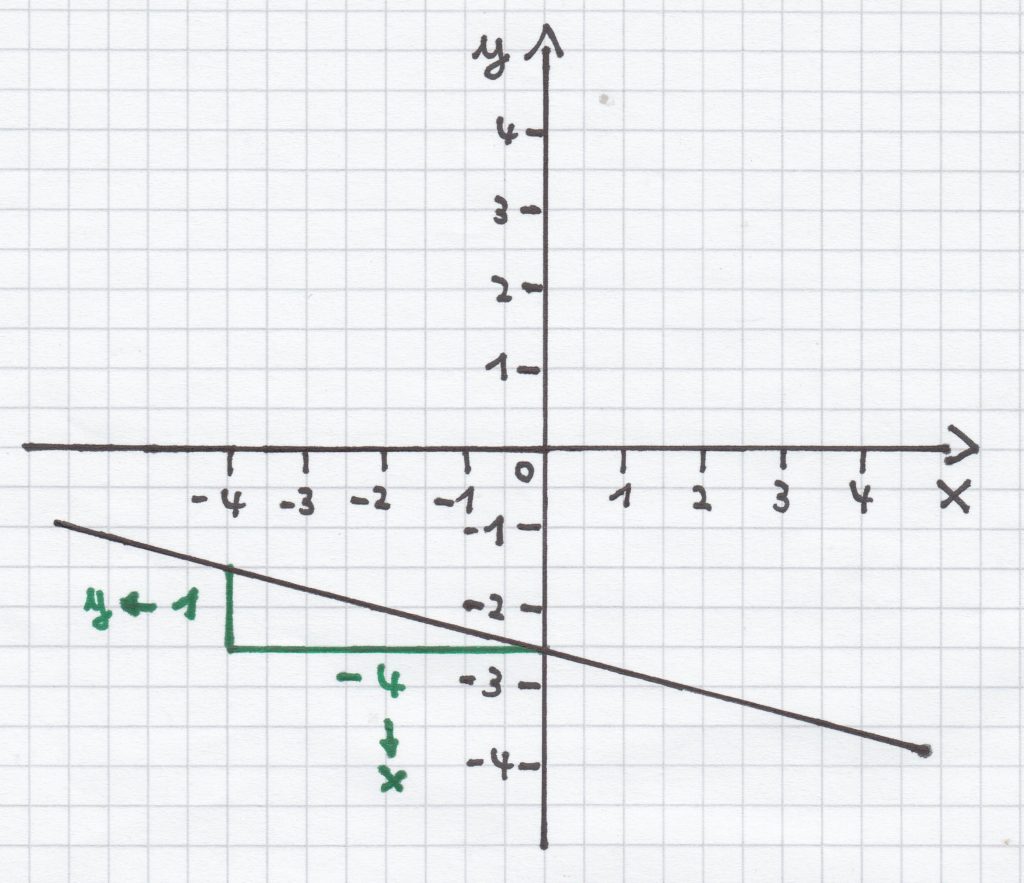
Man sollte sich einprägen, dass rechts und nach oben das Steigungsdreieck mit einer positiven Steigung verläuft, und links und nach oben das Steigungsdreieck mit einer negativen Steigung.
Man sollte aber auch wissen: Die Umkehrung gilt ebenso! Bei einer positiven Steigung kann man daher auch nach links und nach unten das Steigungsdreieck einzeichnen. Bei einer negativen Steigung kann man auch das Steigungsdreieck nach rechts und nach unten einzeichnen. Eine Art des Einzeichnens sollte man sich aber auf jeden Fall einprägen.