1. Allgemeines zu Potenzfunktionen
Der Graph der bekanntesten Potenzfunktion ist die sogenannte Normalparabel. Diese besitzt folgende Funktionsgleichung: f(x) = x2. Alle weiteren Funktionen, die aus einer Potenz bestehen und bei denen die Variable die Basis ist, nennt man Potenzfunktionen.
Hieraus ergibt sich, dass auch die Funktion f(x) = x1 eine Potenzfunktion ist – deren Graph eine Gerade ist, und zwar die 1. Winkelhalbierende.
Das sind alles Potenzfunktionen:
x ↦ x1, die Funktionsgleichung ist y = x1
x ↦ x2, die Funktionsgleichung ist y = x2
x ↦ x3, die Funktionsgleichung ist y = x3
x ↦ x4, die Funktionsgleichung ist y = x4
x ↦ x5, die Funktionsgleichung ist y = x5
x ↦ x6, die Funktionsgleichung ist y = x6
…
1.1 Der Graph von Potenzfunktionen
Die Potenzfunktion x ↦ x1 hat folgenden Graphen:

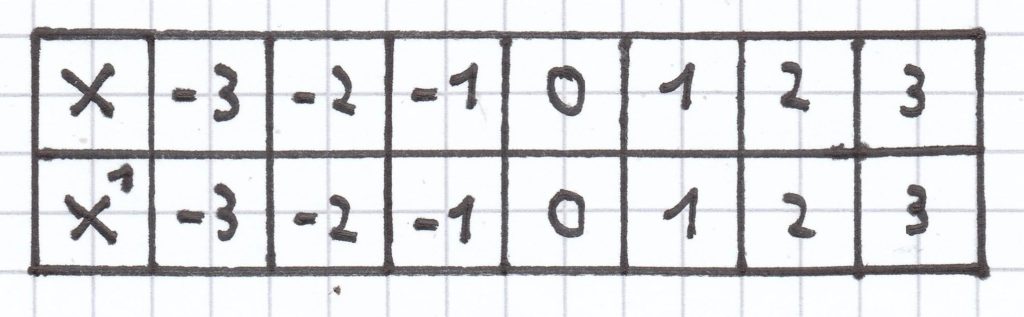
Der Graph der Potenzfunktion x ↦ x1 mit x є ℝ steigt von links nach rechts.
Der Graph ist punktsymmetrisch zum Ursprung/P (0|0). Es gilt nämlich: f(x) = x und f(–x) = –x
Beispiel: f(2) = 2 und f(–2) = –2
Die Funktionsgleichung ist y = x¹
Die Potenzfunktion x ↦ x2 hat diesen Graphen:
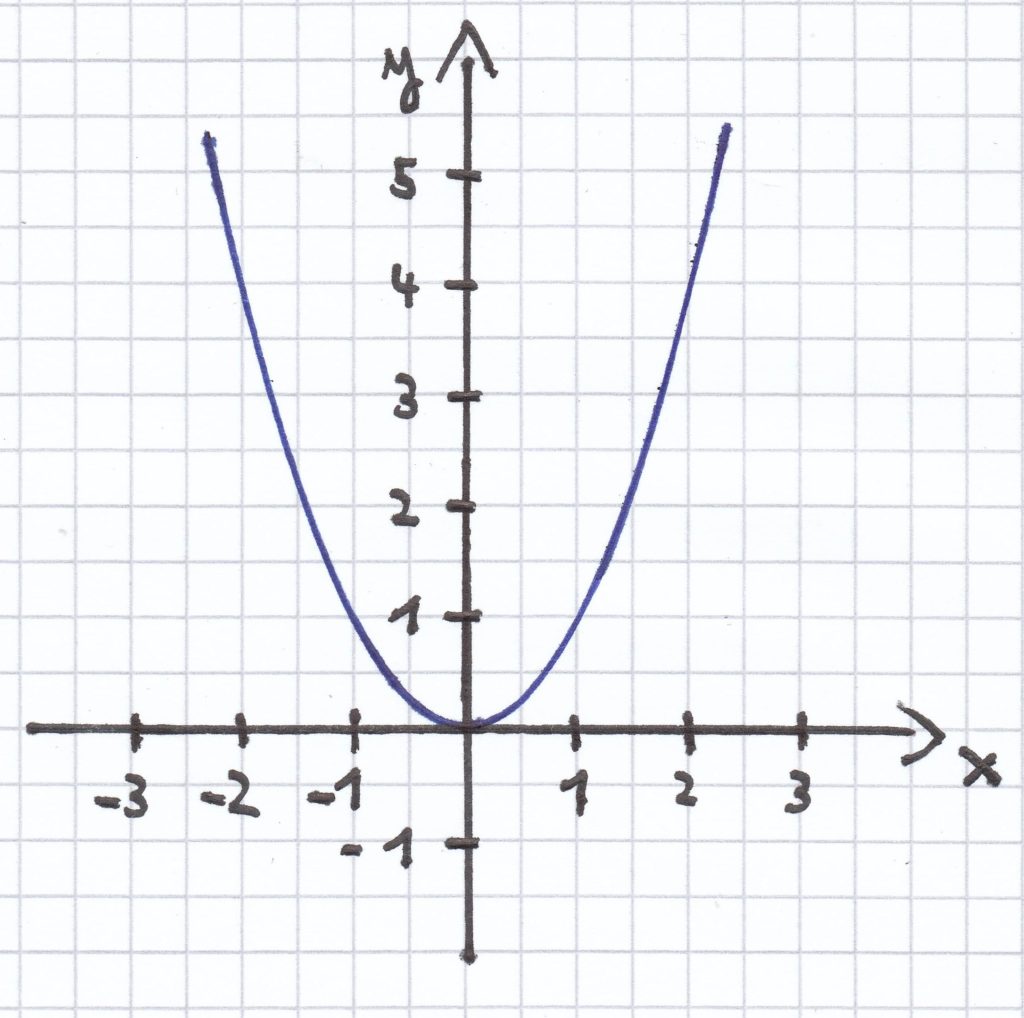
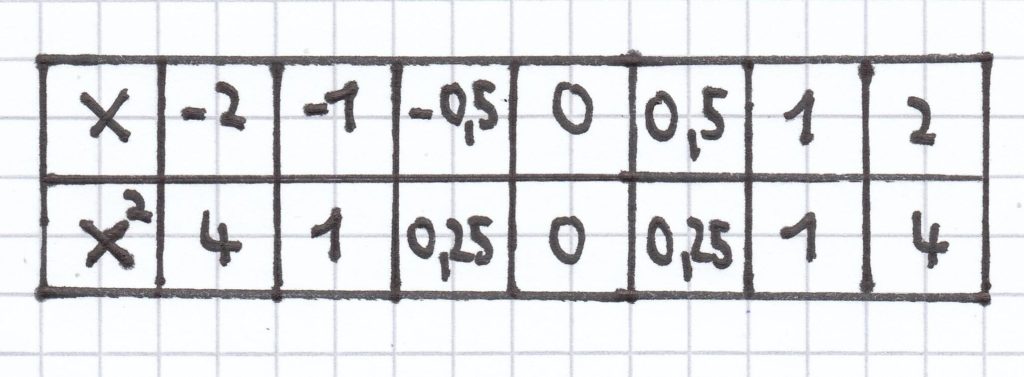
Der Graph der Potenzfunktion x ↦ x2 mit x є ℝ fällt von links nach rechts bis zum Ursprung/P (0|0). Darauf steigt er.
Der Graph ist symmetrisch zur y-Achse. Es gilt nämlich: f(x) = x² und f(–x) = x².
Beispiel: f(2) = (2)² = 4 und f(–2) = (–2)² = 4
Der Graph schmiegt sich in der Nähe des Ursprungs/P (0|0) an die x-Achse an.
Die Funktionsgleichung ist y = x².
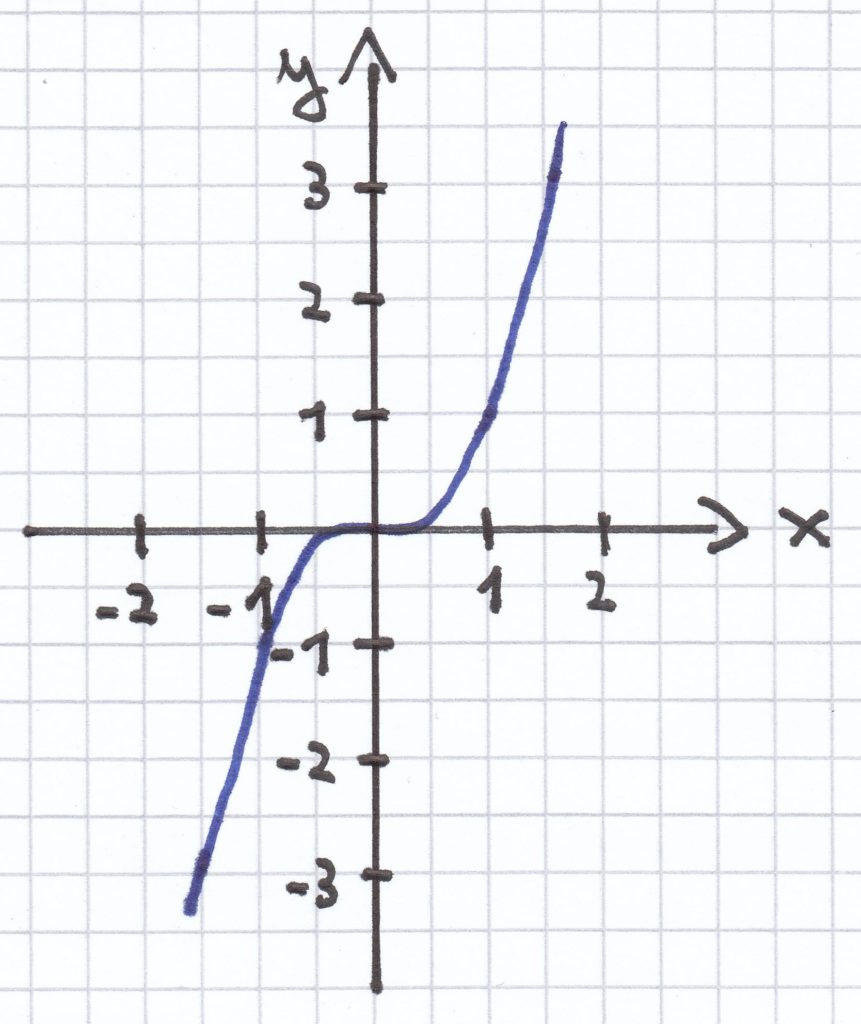
Die Potenzfunktion x ↦ x3 hat diesen Graphen:
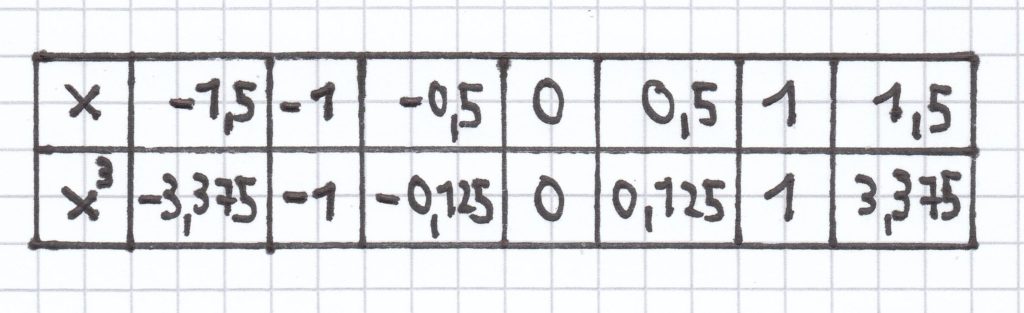
Der Graph der Potenzfunktion x ↦ x3 mit x є ℝ steigt von links nach rechts stetig an.
Der Graph ist punktsymmetrisch zum Ursprung/P (0|0). Es gilt nämlich: f(x) = x³ und f(–x) = –x³
Beispiel: f(2) = (2)³ = 8 und f(–2) = (–2)³ = –8
Der Graph schmiegt sich in der Nähe des Ursprungs/P (0|0) an die x-Achse an.
Die Funktionsgleichung ist y = x³.
Definition:
Eine Funktion, die die Zuordnungsvorschrift x ↦ xn vorweist und somit die Funktionsgleichung f(x) = xn besitzt, nennt man Potenzfunktion (n є N*).
Der Definitionsbereich der Potenzfunktion ist R.
2. Potenzfunktionen mit geradem Exponenten
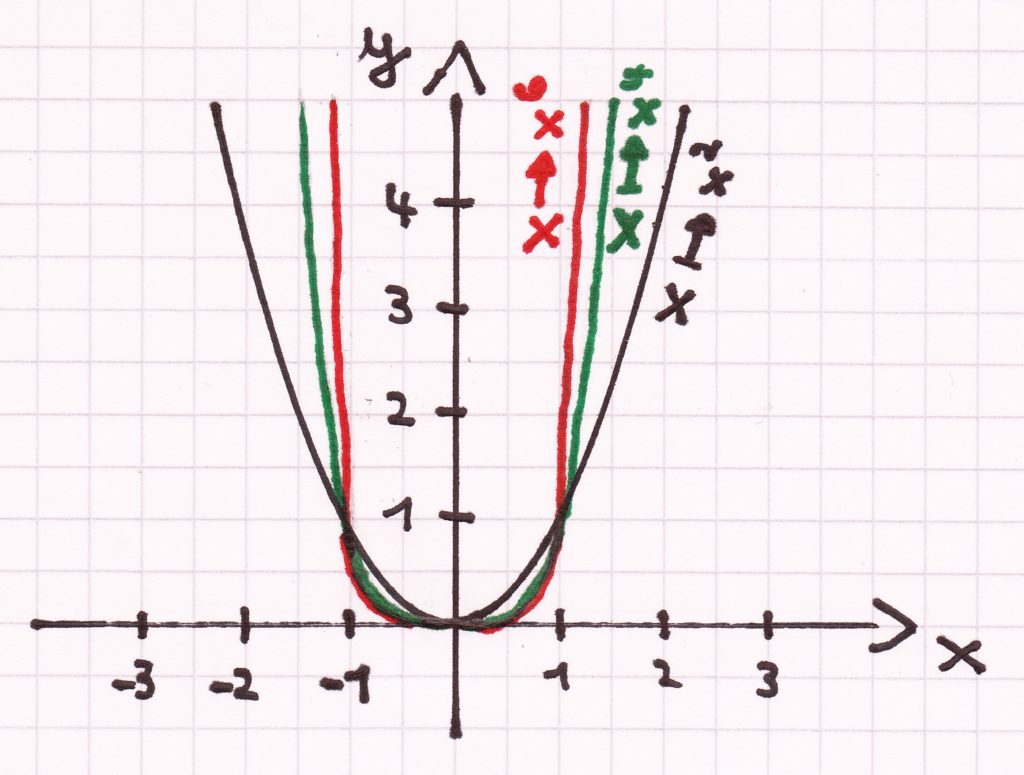
Allgemeine Merkmale von Potenzfunktionen mit geradem Exponenten
- Jede Potenzfunktion x ↦ xn mit geradem Exponenten weist einen Graphen auf, der symmetrisch zur y-Achse ist.
- Alle diese Potenzfunktionen haben drei gemeinsame Punkte: P1 (0|0), P2 = (1|1) und P3 = (–1|1).
- Ist x < 0, so sind die Funktionen streng monoton fallend, ist x > 0, dann sind die Funktionen streng monoton steigend.
3. Potenzfunktionen mit ungeraden Exponenten
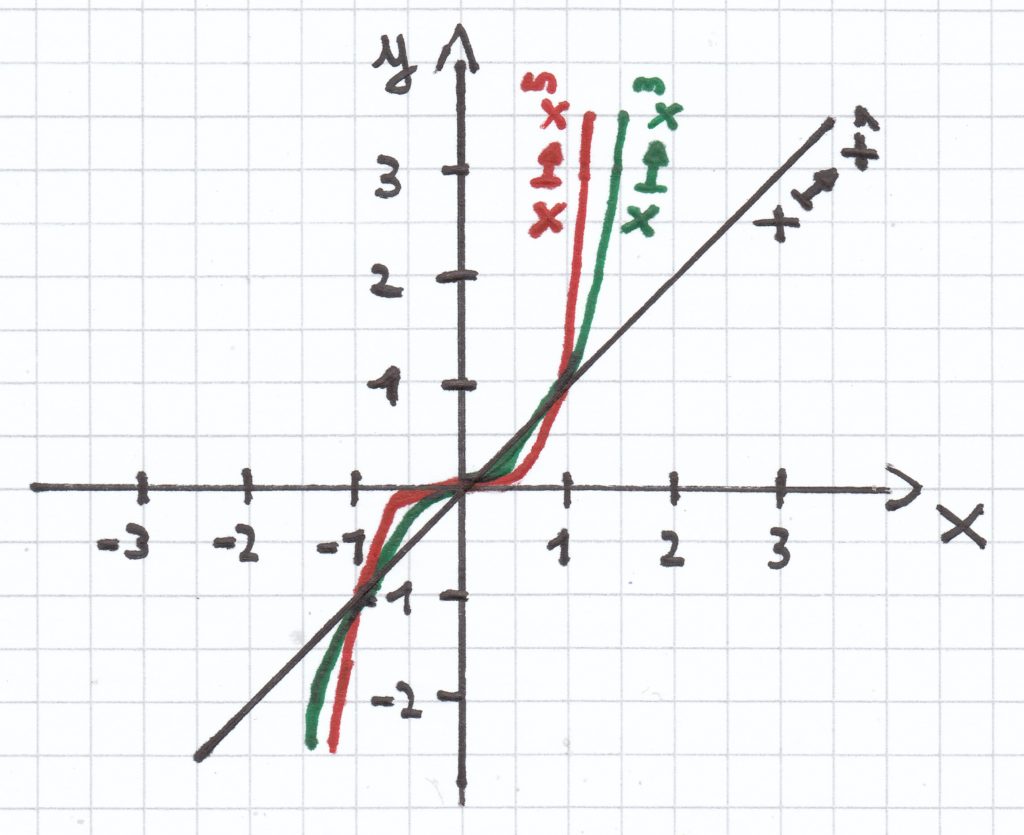
Allgemeine Merkmale von Potenzfunktionen mit ungeraden Exponenten.
- Jede Potenzfunktion x ↦ xn mit ungeradem Exponenten hat einen Graphen, der punktsymmetrisch zum Ursprung/P (0|0) ist.
- Alle diese Potenzfunktionen habe folgende drei gemeinsame Punkte: P1 (0|0), P2 (1|1) und P3 (–1|–1).
- Die Funktionen sind an jeder Stelle streng monoton steigend.