1. Allgemeines zu quadratischen Funktionen
Eine quadratische Funktion kann man auf zweierlei Weise problemlos als granzrationale Funktion zweiten Grades bzw. quadratische Funktion „diagnostizieren“ – entweder anhand ihres Graphen oder ihrer Funktionsgleichung. Der Graph (das zeichnerische Schaubild im Koordinatensystem) einer quadratischen Funktion ist nämlich immer eine Parabel und deren Funktionsgleichung weist immer als höchste Potenz ein x² auf.
Je nach Funktionsgleichung kann hierbei der Graph eine sogenannte Normalparabel sein, eine gestauchte (breitere, ausgehend von Form der Normalparabel) Parabel oder eine gestreckte (schmalere, von der Form der Normalparabel ausgehend) Parabel vorweisen. Alle drei Parabelformen lassen sich von der Funktionsgleichung her bestimmen. Das Gleiche gilt für die Lage der Parabeln im Koordinatensystem, die nach oben oder nach unten geöffnet sein kann und deren Hoch- oder Tiefpunkt irgendwo in einem der vier Quadranten (der vier Achsenabschnitte) liegen kann. Denn auch die Funktionsgleichung kann hierüber genau Auskunft geben.
Oftmals muss man bei quadratischen Funktionen erst bestimmte Äquivalenzumformungen am Funktionsterm vornehmen, um genau sehen zu können, welche Parabelform vorliegt, wie sie geöffnet ist und wo genau im Koordinatensystem ihr Scheitel (das ist der Hoch- bzw. Tiefpunkt der Parabel) liegt.
2. Die einfachste quadratische Funktion: f(x) = x²
Der Graph der einfachsten quadratischen Funktion, f(x) = x², ist eine Normalparabel. Diese sieht dargestellt in einem Koordinatensystem folgendermaßen aus:
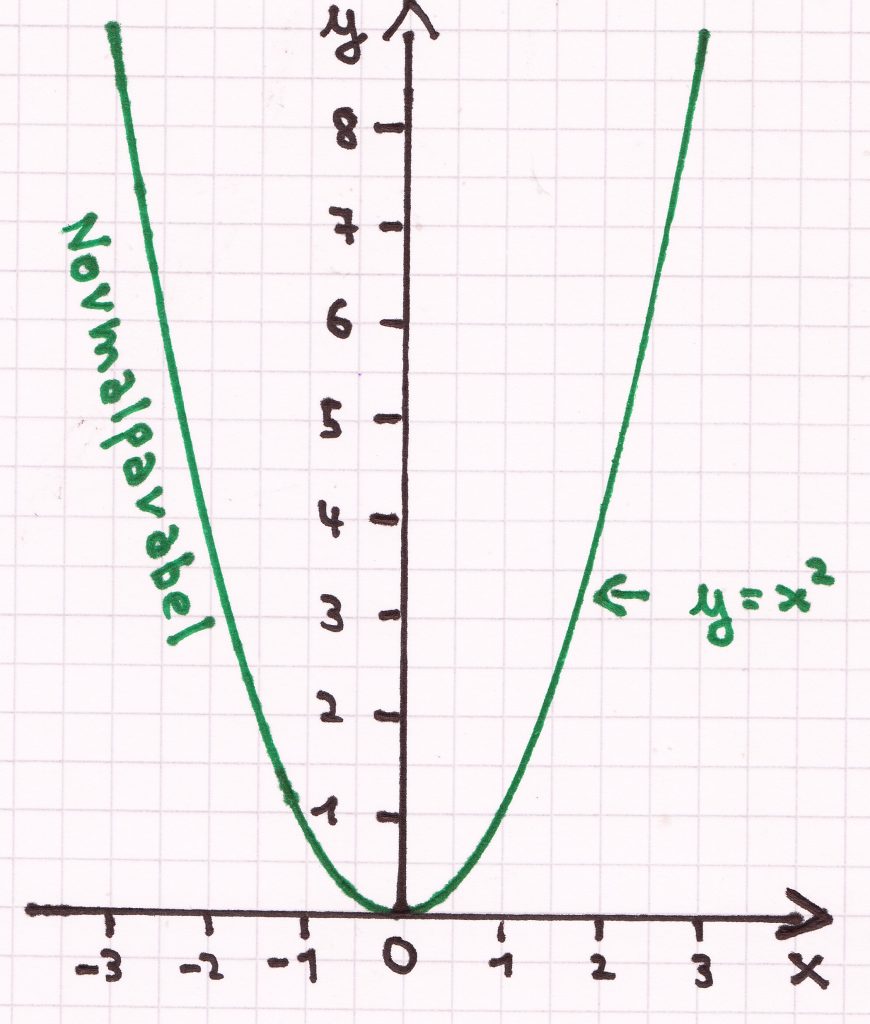
Die Wertetabelle der Funktion f(x) = x² ist hierbei diese:

Merkmale/Charakteristika der Quadratfunktion f mit f(x) = x²
- Achsensymmetrie: Der Graph ist achsensymmetrisch zur y-Achse
- Scheitelpunkt = Tiefpunkt: Der Koordinatenursprung, S (0/0), ist der Scheitelpunkt und und zugleich der tiefste Punkt/Tiefpunkt des Graphen.
- Monotonie: Im 2. Quadranten ist der Graph streng monoton fallend, im 1. Quadranten streng monoton steigen.
3. Verschiebung der Normalparabel auf der 2. Koordinatenachse
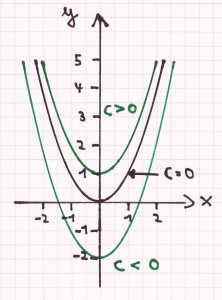
Verschiebt man die Normalparabel entlang der y-Achse, der 2. Koordinatenachse, so ändert sich die Funktionsgleichung f(x) = x². Hinzu kommt nämlich der konstante Wert c. Dadurch verändert sich die Funktionsgleichung dahingehend zu: f(x) = x² + c.
Allgemeine Merkmale der Funktion: f(x) = x² + c
- ist c > 0, dann ist die Normalparabel nach oben verschoben
- ist c < 0, dann ist die Normalparabel nach untern verschoben
Die Funktion f(x) = x² + c ist kongruent/deckungsgleich zu der Funktion f(x) = x². Die Achsensymmetrie, der Scheitelpunkt als Tiefpunkt und die Monotonie der Normalparabel bleiben hierbei erhalten. Nur der Scheitelpunkt der verschobenen Normalparabel ändert sich hin zu: S (0/c).
Beispiele:
Aus dem obigen Graphen kann man daher folgende drei quadratische Funktionen ablesen:
1) Die Normalparabel, die durch den Koordinatenursprung geht und bei der der c-Wert = 0 ist, hat die Funktionsgleichung f(x) = x² .
2) Die nach oben verschobene Normalparabel, bei der der c-Wert der Schnittpunkt mit der y-Achse ist und hier 1 beträgt. Daher ergibt sich die Funktionsgleichung: f(x) = x² + 1.
3) Bei der nach unten verschobenen Normalparabel ist wiederum der c-Wert der Schnittpunkt mit der 2. Koordinatenachse und beträgt hier –2. Deshalb ist hier die Funktionsgleichung: f(x) = x² – 2.
4. Verschiebung der Normalparabel auf der 1. Koordinatenachse
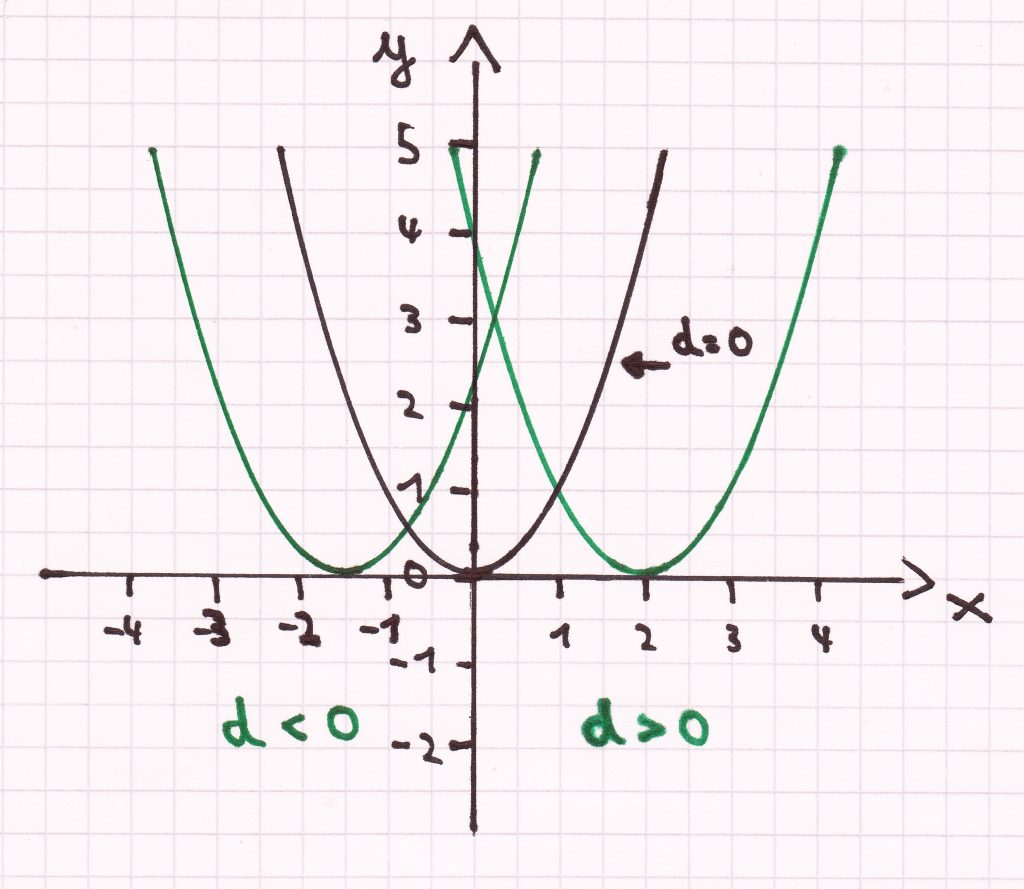
Wenn man die Normalparabel entlang der x-Achse verschiebt, der 1. Koordinatenachse, so verändert sich ebenfalls die Funktionsgleichung f(x) = x². Dies lässt sich in der Form f(x) = (x – d)² wiedergeben. Der d-Wert gibt hierbei die Verschiebung in Richtung der x-Achse an.
Allgemeine Merkmale der Funktion: f(x) = (x – d)²
- ist d > 0, dann ist die Normalparabel nach rechts verschoben
- ist d < 0, dann ist die Normalparabel nach links verschoben
Der Graph der Funktion ist weiterhin kongruent/deckungsgleich zur Normalparabel. Der Scheitelpunkt hat die Koordinaten S (d/0) und ist gleichzeitig der Tiefpunkt der Funktion. Mit der Gleichung x = d erhält man eine Parallele zur y-Achse, die gleichzeitig die Symmetrieachse des Graphen von der Funktion ist.
Beachte, dass der d-Wert nur richtig bestimmt werden, wenn die Funktion die Form f(x) = (x – d)² hat. Achte hierbei auch unbedingt darauf, dass das Minus als Rechenzeichen zum Vorschein kommt.
Beispiele:
Aus den obigen Graphen, kann man folgende Funktionsgleichungen bestimmen:
1) Die Normalparabel, die ihren Scheitel im Koordinatenursprung hat, besitzt den d-Wert 0. Daher ist die Funktionsgleichung: f(x) = (x – 0)² <=> f(x) = (x)² <=> f(x) = x².
2) Bei der nach rechts auf der x-Achse verschobenen Normalparabel ist der d-Wert 2. Daraus ergibt sich diese Funktionsgleichung: f(x) = (x – (+2))² <=> f(x) = (x – 2)².
3) Bei der nach links auf der x-Achse verschobenen Normalparabel ist der d-Wert –1,5. Hieraus ergibt sich diese Funktionsgleichung: f(x) = (x – (–1,5))².
5. Verschiebung der Normalparabel in beliebiger Richtung
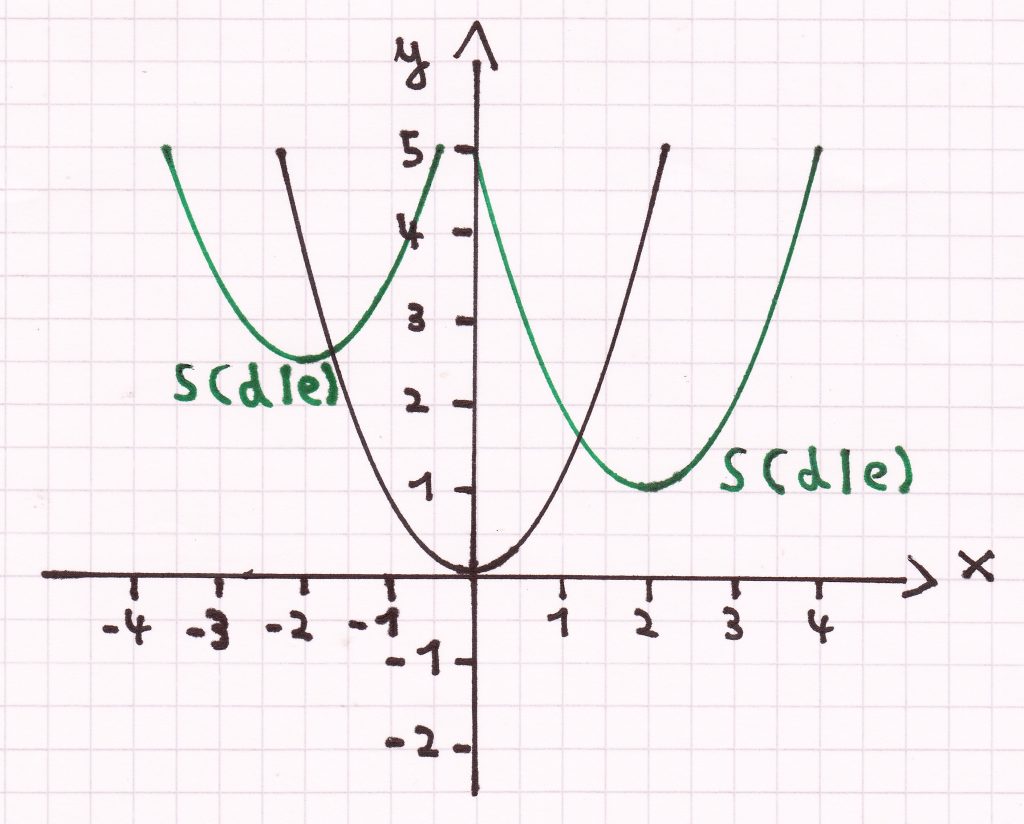
Wenn man nun die Normalparabel entlang der x- und y-Achse verschiebt, so verändert sich die Funktionsgleichung f(x) = x² folgendermaßen: f(x) = (x – d)² + e. Diese Form einer quadratischen Funktion nennt man die Scheitelpunktform.
Allgemeine Merkmale der Funktion: f(x) = (x – d)² + e
Der Graph der Funktion ist kongruent/deckungsgleich zur Normalparabel. Der Scheitelpunkt hat die Koordinaten S (d/e). Die Symmetrieachse lässt sich mit der Gleichung x = d ermitteln. Ist x < d so fällt der Graph der Funktion, ist x > d so steigt der Graph der Funktion an.
Beispiele:
Von den obigen Graphen, kann man folgende Funktionsgleichungen aufstellen:
1) Die Normalparabel, bei der ihr Scheitel im Koordinatenursprung liegt, besitzt den e-Wert 0 und den d- Wert 0. Daher ergibt sich die Funktionsgleichung: f(x) = (x – 0)² + 0 <=> f(x) = x²
2) Bei der nach rechts oben verschobenen Normalparabel ist der e-Wert = 1 und der d-Wert = 2. Hierdurch kann man folgende Funktionsgleichung aufstellen: f(x) = (x – (+2))² + 1 <=> f(x) = (x – 2)² + 1
3) Bei der nach links oben verschobenen Normalparabel ist der e-Wert 2,5 und der d-Wert –2. Daher ergibt sich diese Funktionsgleichung: f(x) = (x – (–2))² + 2,5
Oftmals liegt eine quadratische Funktion in der sogenannten Normalform, f(x) = x² + px + q, vor. Die Funktion kann man dann durch ein quadratisches Ergänzen in die Scheitelpunktform bringen.
Die Umwandlung der Normalform hin zur Scheitelpunktform geht auch über diese Gleichungen:

,
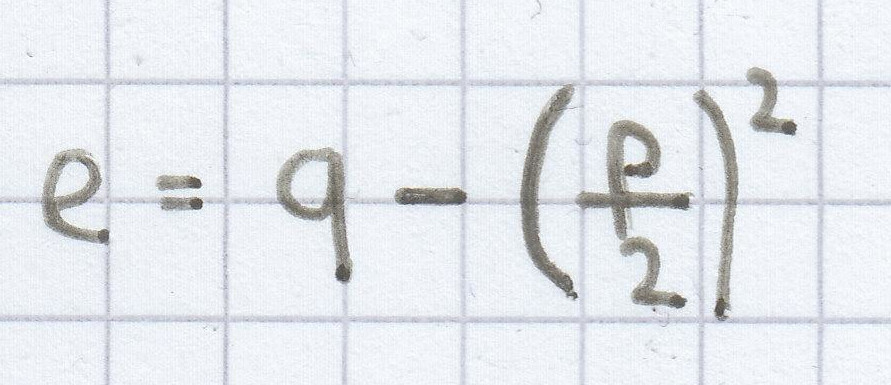
.