
1. Allgemeines zum Umrechnen von Größen
Bei Größen müssen im Fach Mathematik die ermittelnden Größenangaben oft umgerechnet werdet, und zwar in eine größere oder eine kleinere Maßeinheit. Das kann aus zweierlei Gründen notwendig sein.
- Damit man verschiedene Größenangaben gleicher Größen (z. B. Längen wie 5 m und 1200 mm oder Zeitdauern wie 5 h und 216000 s) bestmöglich vergleichen kann, müssen die Maßeinheiten jeweils gleich sein (z. B. umgerechnet in Längen wie 5 m und 1,2 m oder umgerechnet in Zeitdauern wie 5 h und 1 h).
- Wenn die Maßzahl einer Größenangabe sehr groß (z.B. Längen wie 50000000 cm oder Zeitdauern wie 864000 s) oder sehr klein (z. B. Längen wie 0,0000098 km oder Zeitdauern wie 0,02 h) ist und dementsprechend viele Zahlen vor oder nach dem Komma stehen, sollte man immer eine größere (z.B. umgerechnet in die Länge wie 500 km oder umgerechnet in die Zeitdauer wie 10 d) oder kleinere Maßeinheit (z. B. umgerechnet in die Länge wie 9,8 mm oder umgerechnet in die Zeitdauer wie 1,2 min) wählen. Denn dann kann man viel besser sehen, wie groß die Größe wirklich ist.
2. Umrechnen von Größen
Je nach Längeneinheiten, Einheiten für Zeitdauern, Gewichtseinheiten und Einheiten für die Fläche und den Rauminhalt gelten für die Umrechnung in andere Einheiten der gleichen Größe verschiedene Umrechnungszahlen. Nachfolgend ist veranschaulicht, wie eine richtige Umrechnung von Längeneinheiten, Gewichtseinheiten und Einheiten von Zeitdauern gemacht wird.
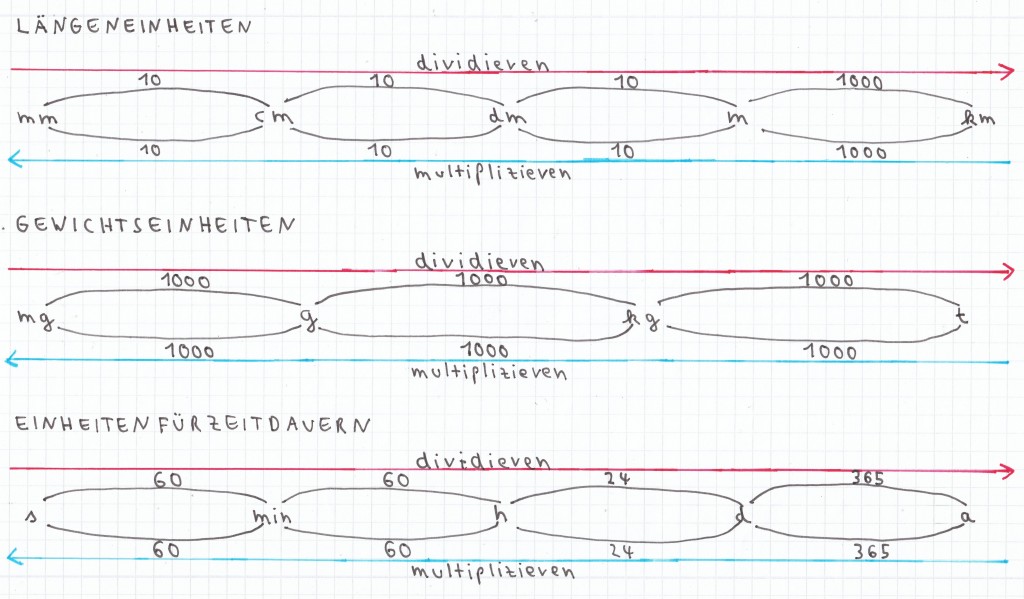
Durch diese bildliche Veranschaulichung soll deutlich gemacht werden, dass von links nach rechts die Maßeinheiten der Größen Länge, Gewicht und Zeitdauer größer werden (rote Pfeilrichtung). Hierbei wird stets mit einer bestimmten Umrechnungszahl eine Division durchgeführt. Umgekehrt werden dagegen die Maßeinheiten der gleichen Größen von links nach rechts kleiner (blaue Pfeilrichtung). Hierbei wird jeweils mit einer bestimmten Umrechnungszahl eine Multiplikation durchgeführt.
2.1 Umrechnen der Größe Länge
Hierbei ist bei der Größe Länge die kleinste gängige Maßeinheit im Fach Mathematik mm (Millimeter), die nächst größere cm (Zentimeter), die wiederum nächst größere dm (Dezimeter), die daraufhin nächst größere m (Meter) und die darauffolgende letzte relevante Maßeinheit km (Kilometer). Die Umrechnungszahl von mm in cm ist hierbei 10, von cm in dm ebenfalls 10 und von dm in m ebenso 10, von m in km hingegen beträgt die Umrechnungszahl 1000. Die gleichen Umrechnungszahlen gelten natürlich auch in umgekehrter Richtung! Daher ist die Umrechnungszahl von km in m 1000, die Umrechnungszahl von m in dm 10, von dm in cm ebenfalls 10 und von cm in mm ebenso 10.
2.2 Umrechnen der Größe Gewicht
Bei der Größe Gewicht ist hingegen die kleinste gängige Maßeinheit im Fach Mathe mg (Milligramm), die nächst größere g (Gramm), die wiederum nächst größer kg (Kilogramm) und die darauffolgende letzte relevante t (Tonne). Die Umrechnungszahl von mg in g ist hierbei 1000, von g in kg ebenfalls 1000 und von kg in t ebenso 1000. Auch hier gelten natürlich in umgekehrter Richtung die gleichen Umrechnungszahlen! Deshalb ist die Umrechnungszahl von t in kg 1000, von kg in g ebenfalls 1000 und von g in mg ebenso 1000.
2.3 Umrechnen der Größe Zeitdauer
Bei der Größe Zeitdauer ist hingegen die kleinste gängige Maßeinheit im Fach Mathematik s (Sekunde), die nächst größere min (Minute), die wiederum nächst größere h (Stunde), die daraufhin nächst größere d (Tag) und die darauffolgende letzte relevante a (Jahr). Die Umrechnungszahl von s in min ist hierbei 60, von min in h ebenfalls 60, von h in d 24 und von d in a 365. Natürlich gelten auch hier in die umgekehrte Richtung die gleichen Umrechnungszahlen! Daher ist die Umrechnungszahl von a in d 365, von d in h 24, von h in min 60 und von min in s ebenfalls 60. (Anmerkung: Bei einem Schaltjahr umfasst ein Jahr hingegen 366 Tage. In der Zinsrechnung hat ein Jahr hingegen nur 360 Tage).
Damit man nun eine Länge, ein Gewicht oder eine Zeitdauer jeweils dahingehend umrechnen kann, dass deren Maßeinheit stets größer wird, muss man ihre Maßzahl mit einer bestimmten Umrechnungszahl dividieren. Hält man diese bestimmte Umrechnungszahl stets ein, so kann man jeweils die Maßeinheit der Größenangabe ohne Probleme vergrößern (Beispiele: 500 mm wird mit der Umrechnungszahl 10 dividiert, so erhält man 50 cm. Möchte man nun die Maßeinheit weiter zur nächst größeren hin umrechnen, so muss man 50 cm wiederum durch die Umrechnungszahl 10 dividieren. Hierbei ergibt sich dann die Größenangabe 5 dm usw.; 2000000 mg wird mit der Umrechnungszahl 1000 dividiert, so erhält man 2000 g. Möchte man nun die Maßeinheit wiederum weiter zur nächst größeren hin umrechnen, so muss man 2000 g wiederum durch die Umrechnungszahl 1000 dividieren. Hierbei ergibt sich dann die Größenangabe 2 kg usw.; 25200 s wird mit der Umrechnungszahl 60 dividiert, so erhält man 420 min. Möchte man nun die Maßeinheit weiter zur nächst größeren hin umrechnen, so muss man 420 min wiederum durch die Umrechnungszahl 60 dividieren. Hierbei ergibt sich dann die Größenangabe 7 h usw.).
Damit man nun eine Länge, ein Gewicht oder eine Zeitdauer stets dahingehend umrechnen kann, dass deren Maßeinheit jeweils kleiner wird, muss man ihre Maßzahl mit einer bestimmten Umrechnungszahl multiplizieren. Hält man hier ebenfalls die bestimmte Umrechnungszahl stets ein, dann kann man jeweils die Maßeinheit der Größenangabe wiederum problemlos verkleinern (Beispiele: 50 km wird mit der Umrechnungszahl 1000 multipliziert, so erhält man 50000 m. Möchte man nun die Maßeinheit wiederum weiter zur nächst kleineren hin umrechnen, dann muss man 50000 m mit der Umrechnungszahl 10 multiplizieren. Hierbei ergibt sich dann die Größenangabe 500000 dm usw.; 7 t wird mit der Umrechnungszahl 1000 multipliziert, so erhält man 7000 kg. Möchte man nun die Maßeinheit wiederum weiter zur nächst kleineren hin umrechnen, dann muss man 7000 kg wiederum mit der Umrechnungszahl 1000 multiplizieren. Dadurch ergibt sich dann die Größenangabe 7000000 g; 5 a wird mit der Umrechnungszahl 365 multipliziert, so erhält man 1825 d. Möchte man nun die Maßeinheit wiederum zur nächst kleineren hin umrechnen, so muss man 1825 d mit der Umrechnungszahl 24 multiplizieren. Hierdurch ergibt sich dann die Größenangabe 43800 h usw.).
Genauso wie bei den Größen Länge, Gewicht und Zeitdauer bei der Umrechnung in andere Einheiten eindeutige Umrechnungszahlen gelten, gibt es für die Größen Fläche und Rauminhalt ebenso welche. Nachfolgend sind diese wieder bildhaft veranschaulicht.
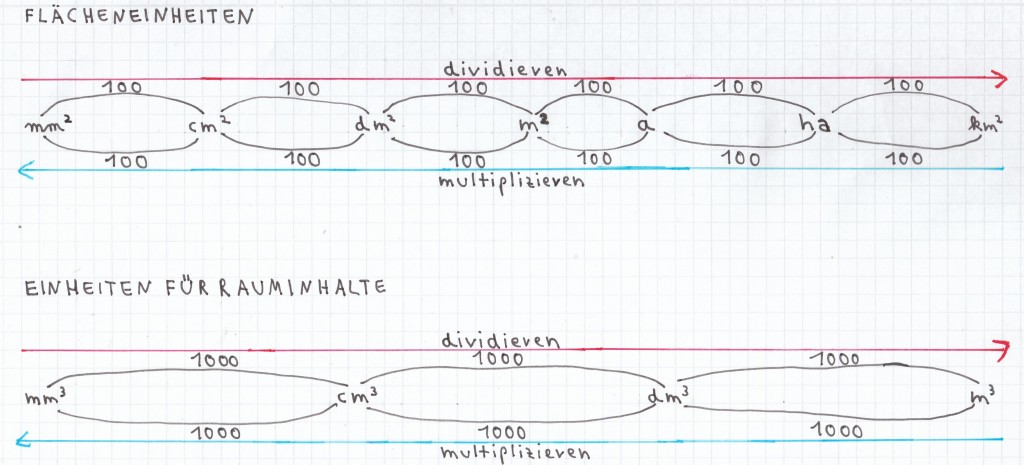
Durch diese bildhafte Veranschaulichung soll ebenso aufgezeigt werden, dass von links nach rechts die Maßeinheiten der Größen Flächen und Rauminhalt (Volumen) größer werden (rote Pfeilrichtung). Hierbei wird jeweils mit einer bestimmten Umrechnungszahl eine Division durchgeführt. Dagegen werden umgekehrt die Maßeinheiten derselben Größen von rechts nach links kleiner (blaue Pfeilrichtung). Hierbei wird stets mit einer bestimmten Umrechnungszahl eine Multiplikation durchgeführt.
2.4 Umrechnen der Größe Fläche
Hierbei ist im Fach Mathematik bei der Größe Fläche die kleinste gängige Maßeinheit mm² (Quadratmillimeter), die nächst größere cm² (Quadratzentimeter), die wiederum nächst größere dm² (Quadratdezimeter) die daraufhin nächst größere m² (Quadratmeter), die darauffolgende nächst größere a (Ar) und die daraufhin folgende Maßeinheit ha (Hektar) und die darauffolgende letzte relevante km² (Quadratkilometer). Die Umrechnungszahl von mm² in cm² ist hierbei 100, von cm² in dm² ebenso 100, von dm² in m² ebenfalls 100, von m² in a beträgt die Umrechnungszahl ebenso 100 und von a in ha ebenfalls 100 sowie von ha in km² auch 100. Die Umrechnungszahlen gelten natürlich auch in umgekehrter Richtung! Daher ist die Umrechnungszahl von km² in ha 100, von ha in a ebenfalls 100, von a in m² ebenso 100, von m² in dm² ebenfalls 100, von dm² in cm² ebenso 100 sowie von cm² in mm² auch 100.
2.5 Umrechnen der Größe Rauminhalt (Volumen)
Bei der Größe Rauminhalt (Volumen) ist im Fach Mathematik hingegen die kleinste gängige Maßeinheit mm³, die nächst größere cm³, die daraufhin nächst größere dm³ und die darauffolgende letzte relevante m³. Die Umrechnungszahl von mm³ in cm³ ist hierbei 1000, von cm³ in dm³ ebenso 1000 und von dm³ in m³ ebenfalls 1000. Natürlich gelten auch hier die Umrechnungszahlen in umgekehrter Richtung! Daher ist die Umrechnungszahl von m³ in dm³ 1000, von dm³ in cm³ ebenfalls 1000 und von cm³ in mm³ ebenso 1000 (Anmerkung: Für Rauminhalte/Volumen gibt es noch folgende spezielle Beziehungen verschiedener Maßeinheiten: 1 l sind 1 dm³; 1 ml sind 1 cm³; 1 l sind 1000 ml; 1 hl sind 100 l).
Damit man nun eine Fläche oder ein Rauminhalt stets dahingehend umrechnen kann, dass deren Maßeinheit jeweils größer wird, muss man ihre Maßzahl mit einer bestimmten Umrechnungszahl dividieren. Hält man diese Umrechnungszahl jeweils ein, so kann man auch stets die Maßeinheit der Größenangabe problemlos verkleinern (Beispiele: 90000 mm² wird mit der Umrechnungszahl 100 dividiert, so erhält man 900 cm². Möchte man nun die Maßeinheit weiter zur nächst größeren hin umrechnen, so muss man 900 cm² wiederum durch die Umrechnungszahl 100 dividieren. Hierdurch erhält man dann die Größenangabe 9 dm² usw.; 2000000 mm³ wird durch die Umrechnungszahl 1000 dividiert, so erhält man 2000 cm³. Möchte man nun die Maßeinheit weiter zur nächst größeren hin umrechnen, so muss man 2000 cm³ wiederum durch die Umrechnungszahl 1000 dividieren. Dadurch erhält man die Größenangabe 2 dm³ usw.).
Damit man hingegen nun eine Fläche oder ein Rauminhalt stets derart umrechnen kann, dass deren Maßeinheit jeweils kleiner wird, muss man ihre Maßzahl mit einer bestimmten Umrechnungszahl multiplizieren. Hält man hier ebenso die bestimmte Umrechnungszahl stets ein, so kann man jeweils die Maßeinheit der Größenangabe problemlos verkleinern (Beispiele: 5 km² wird mit der Umrechnungszahl 100 multipliziert, so erhält man 500 ha. Möchte man nun die Maßeinheit weiter zur nächst kleineren hin umrechnen, so muss man 500 ha wiederum mit der Umrechnungszahl 100 multiplizieren. Hierdurch ergibt sich die Größenangabe 50000 a; 30 m³ wird mit der Umrechnungszahl 1000 multipliziert, so erhält man 30000 dm³. Möchte man nun die Maßeinheit weiter zur nächst kleineren hin umrechnen, so muss man 30000 dm³ wiederum mit der Umrechnungszahl 1000 multiplizieren. Hierdurch erhält man die Größenangabe 30000000 cm³ usw.).
2.6 Umrechnen der Größe Geldwert
Da es bei der Größe Geldwert nur zwei Maßeinheiten gibt, spielt diese Größe im Fach Mathematik bei Größen-Umrechnungen kaum eine Rolle. Trotzdem sollte man die Umrechnungszahl hierfür wissen. Hierzu sollte man sich nur Folgendes einprägen.
1 Euro = 100 Cent
Dadurch weiß mann, dass die Umrechnungszahl von Cent in Euro und von Euro in Cent jeweils 100 ist. Die Maßeinheit für Cent ist hierbei ct, die für Euro €.
2.7 Tipps zum Umrechnen von Größen
Falls ein Schüler bei der Umrechnung von Größen Probleme hat, sollte eine Nachhilfe vier Punkte aufgreifen:
- Das Auswendiglernen der verschiedenen Maßeinheiten und das natürlich der Reihenfolge nach (von der kleinsten oder größten her beginnend)
- Das Auswendiglernen der Umrechnungszahlen
- Das Üben der Grundrechenarten Multiplikation und/oder Division
- Das Üben von Dezimalzahlen
Im Fach Mathe treten immer wieder in verschiedenen Klassenstufen Aufgaben auf, in denen die Maßeinheiten von Größenangaben richtig umgerechnet werden müssen. Daher ist ein korrektes Beherrschen überaus wichtig, da das Umrechnen immer auch schon Punkte gibt und somit in die Note einfließt.