1. Allgemeines zu biquadratischen Gleichungen
Hat eine Gleichung zwei Variablen die jeweils die Potenz hoch zwei enthalten, wie beispielsweise die Gleichung x4 – 10x2 + 9 = 0, dann liegt in Mathe eine sogenannte biquadratische Gleichung vor. Denn die Gleichung kann man ja auch mittels einer algebraischen Umformung/Anwendung eines Potenzgesetzes so schreiben:
4(x2)2 – 10x2 + 9
(so zeigt sich eindeutig das Zwei- bzw. Biquadratische solcher Gleichungen).
Dadurch, dass eine biquadratische Gleichung gewissermaßen eine quadratische Gleichung mitenthält, kann man diese auch auf jene zurückführen.
2. Das Lösen biquadratischer Gleichungen
Eine biquadratische Gleichung löst man, indem man mittels einer Substitution die biquadratische Gleichung auf eine quadratische Gleichung hin umwandelt.
Man substituiert/ersetzt hierbei, indem man diese Gleichung anwendet:
x2 = z
Die Substitution macht man dann konkret Folgendermaßen:
x4 wird zu z2
und
x² wird zu z
x4 – 10x2 + 9 wird zu z2 – 10z + 9
Die durch Substitution erhaltene quadratische Gleichung kann man nun mittels der p-q-Formel oder mittels quadratischen Ergänzens lösen.
Falls die quadratische Gleichung eine oder zwei Lösungen hat, muss man darauf die Substitution wieder rückgängig machen. Das macht man folgendermaßen
x² = z | √
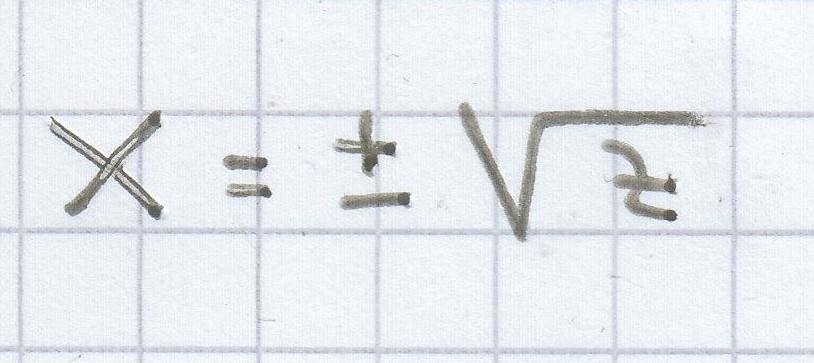
2.1 Vier Lösungen bei einer biquadratischen Gleichung
Es ist diese biquadratische Gleichung gegeben:
x4 – 10x2 + 9 = 0.
Mittels Substitution erhält man diese quadratische Gleichung:
z2 – 10z + 9
Mittels p-q-Formel ergeben sich folgende Lösungen:
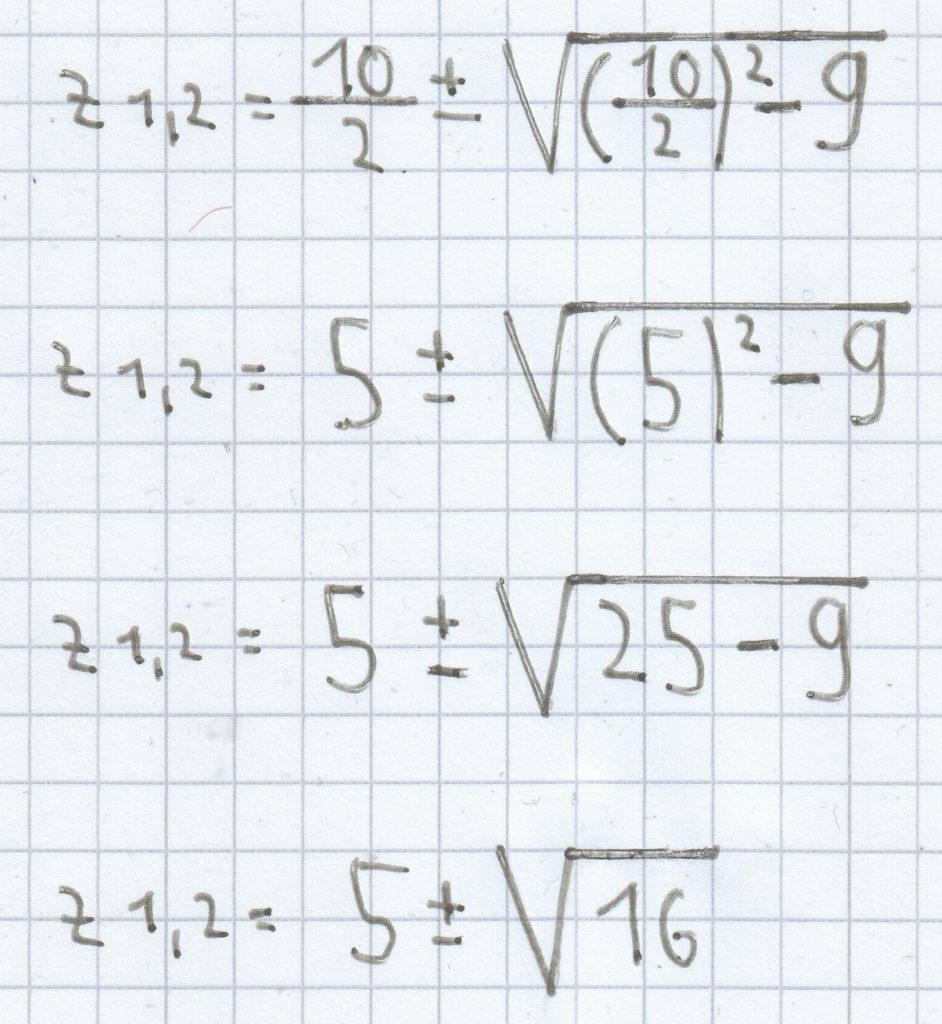
z1,2 = 5 ± 4
z1 = 5 + 4
z1 = 9
z2 = 5 – 4
z2 = 1
Mittels quadratischen Ergänzens erhält man diese Lösungen:
z² – 10z + 9 = 0 | – 9
z² – 10 = –9
z² – 10 + 25 = –9 + 25
(z – 5)² = 16 | √
z – 5 = ± 4 | + 5
z1 = 5 + 4
z1 = 9
z2 = 5 – 4
z2 = 1
Das Auflösen der Substitution:
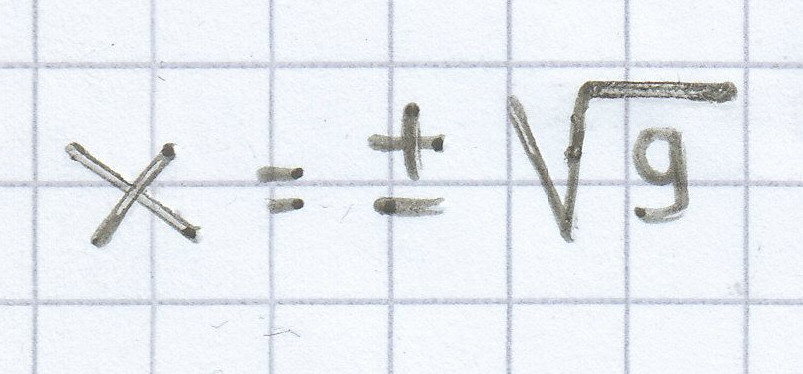
x1,2 = ± 3
x1 = 3
x2 = –3
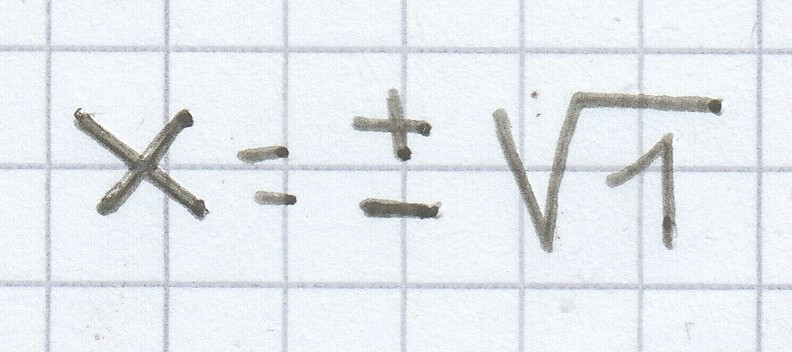
x3,4 = ± 1
x3 = 1
x4 = –1
Die Lösungsmenge der biquadratischen Gleichung x4 – 10x² + 9 = 0 ist:
L = {–3; –1; 1; 3}