1. Allgemeines zur Wahrscheinlichkeitsrechnung
Karten- und Glücksspiele faszinieren Menschen über die Maßen. Das gilt ganz besonders, wenn man dadurch auch noch Geld gewinnen kann. Schließlich macht es nahezu jedem Spaß durch Spielen Geld zu gewinnen. Daher gibt es auch weltweit unzählige Kasinos und Spielbanken, die das einem ermöglichen – vorausgesetzt man ist mindestens 18 Jahre alt. Glücksspiele sind nämlich bekanntlich auch sehr gefährlich, da sie schnell süchtig machen – und man hierbei schnell jede Menge Geld verlieren kann. Aus diesem Grund macht hier auch eine Altersbegrenzung einen großen Sinn. Aber auch als Erwachsener sollte man sich stets im Klaren sein: Bei Karten- und bei Glücksspielen, die bei Kasinos und Spielbanken zum Einsatz kommen, ist die Wahrscheinlichkeit immer zu Ungunsten des Spielenden bzw. wie man so schön sagt: „Die (Spiel-)Bank gewinnt immer!“

In Mathe in der Wahrscheinlichkeitsrechnung geht es nun darum, bei einem bestimmten zufälligen Ereignis ganz genau die Wahrscheinlichkeit zu bestimmen. Hierzu greift man auf sogenannte Zufallsexperimente (beispielsweise mit Münzen, Karten Roulette) zurück, deren Ergebnisse auf die Realität (wie zum Beispiel auf Spielbanken- und Casinowelten) übertragbar sind.
2. Grundbegriffe der Wahrscheinlichkeitsrechnung
2.1 Zufallsexperiment
Ein Zufallsexperiment basiert, wie der Name es schon sagt, nur auf Zufall. Also alle Ausgänge solch eines Experiments sind einzig und allein vom Zufall abhängig.
Beispiele:
Das Werfen einer Münze; das Würfeln mit einem Würfeln; der Ausgang bei einem Roulette-Wurf; das Ziehen einer Kugel aus einem Gefäß, in dem sich verschiedenfarbige Kugeln befinden; das Ziehen einer Karte aus einem Stapel Karten; das Drehen eines Glücksrads, das in verschiedene Zahlen oder Farben unterteilt ist.
2.2 Ergebnismenge Ω
Die Ergebnismenge Ω gibt immer die Menge aller möglichen Ergebnisse eines Zufallsexperiment an.
Beispiele:
Bei einer Münze mit Kopf und Zahl ist Ω = {Kopf; Zahl}; bei einem Würfel, der aus sechs Zahlen besteht, ist Ω = {1; 2; 3; 4; 5; 6}; bei einem Gefäß, in dem sich rote, blaue und grüne Kugeln befinden, ist Ω = {rot; blau; grün}.
2.3 Ereignis E
Das Ereignis E ist immer eine Teilmenge der Ergebnismenge Ω. Das Ereignis ist hierbei immer eine eingegrenzte Möglichkeit aller Möglichkeiten der Ergebnismenge.
Beispiele:
Das Ereignis: „Zahl“ bei einem Münzwurf, E = {Zahl} ⊂ Ω; die ungeraden Zahlen bei einem Würfelwurf, E = {1; 3; 5} ⊂ Ω; die Bildkarten bei einem Kartenspiel, E = {Bube; Dame; König} ⊂ Ω.
2.31 Elementare Summenregel
Um in Mathe die Wahrscheinlichkeit eines Ereignisses zu berechnen, gilt folgende einfache Regel: die elementare Summenregel.
Können bei einem Zufallsversuch mehrere Ergebnisse auftreten und man möchte die Wahrscheinlichkeit wissen, dass das Ergebnis oder diese Ergebnisse eintreffen, so fasst man jene zu einem Ereignis zusammen. Alle zu dem Ereignis E gehörenden Ergebnisse a1, a2, a3,…, am weisen dann diese Wahrscheinlichkeit P(E) auf:
P(E) = P(a1) + P(a2) + P(a3) + … + P(am)
Beispiele:
Beim Würfeln das Auftreten der Zahlen 1, 3, 5 und 6:
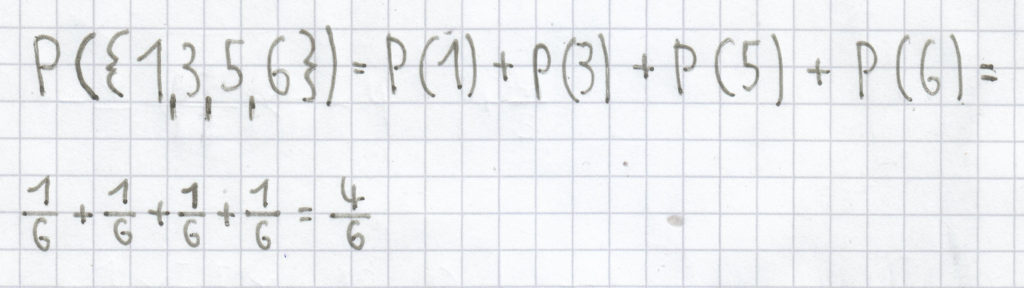
.
Beim Drehen eines Glücksrads, das aus 10 Zahlen besteht und 10 gleichgroßen Feldern, und die Zahlen 2, 5, 7, 8 auftreten:
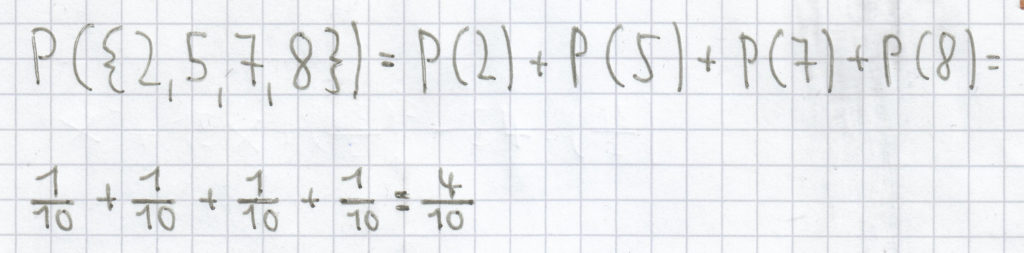
.
2.4 Elementarereignis
Das Elementarereignis ist ein Ereignis, das immer nur aus einem einzigen Ergebnis besteht.
Beispiele:
Beim Münzwurf ist {Zahl} ein Elementarereignis; beim Würfel ist die Augenzahl {4} ein Elementarereignis; bei einem Kartenspiel {Karo Bube}.
2.5 Laplace-Experiment
Bei einem Laplace-Experiment handelt es sich um ein Zufallsexperiment, bei dem alle Elementarereignisse mit gleichbleibender Wahrscheinlichkeit auftreten. Diese gleich bleibende Wahrscheinlichkeit der Elementarereignisse kann man mittels der sogenannten Laplace-Regel berechnen.
Die Wahrscheinlichkeit P(E) eines Ereignisses, das einer gleich bleibenden Wahrscheinlichkeit unterliegt, kann man folgendermaßen berechnen:

Beispiele:
Eine Münze besteht aus Kopf und Zahl. Die Wahrscheinlichkeit, dass das Ergebnis Kopf auftritt ist:
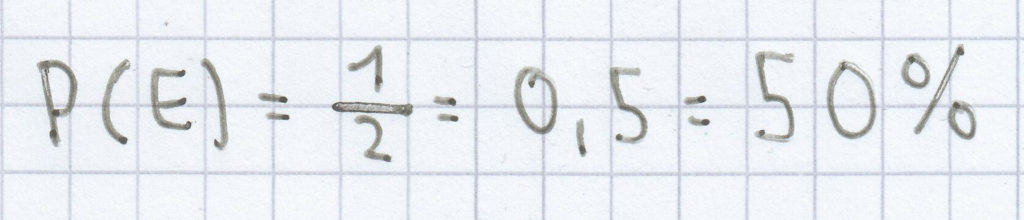
. Demzufolge ist auch die Wahrscheinlichkeit, dass bei einem Münzwurf das Ergebnis Zahl auftritt:
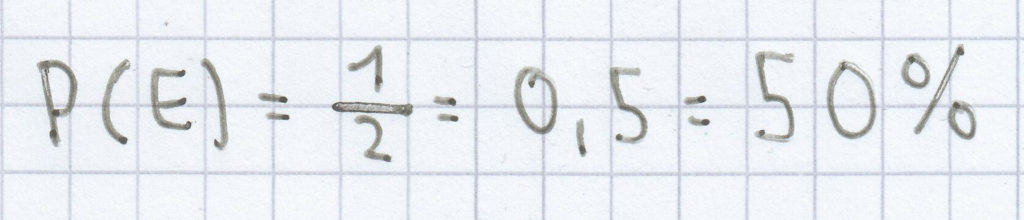
.
Ein Würfel besteht aus den Zahlen 1, 2, 3, 4, 5, 6. Dass Zahl 5 als Ergebnis auftritt, hat die Wahrscheinlichkeit:
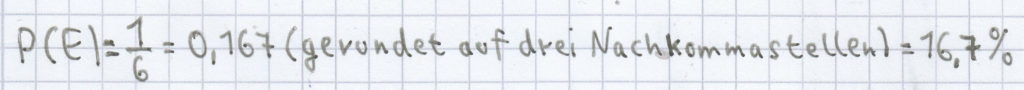
. Daher ist auch die Wahrscheinlichkeit, dass als Ergebnis 1, 2, 3, 4 oder 6 gewürfelt wird:
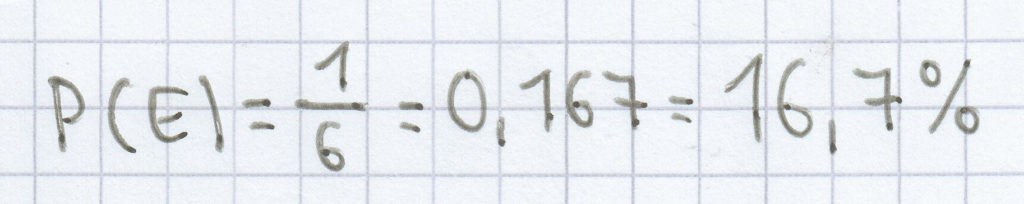
.
Ein Roulette-Spiel besteht aus 36 Feldern plus der Null als Feld. Die Wahrscheinlichkeit, dass als Ergebnis eine 10 beim Roulette auftritt, ist daher:
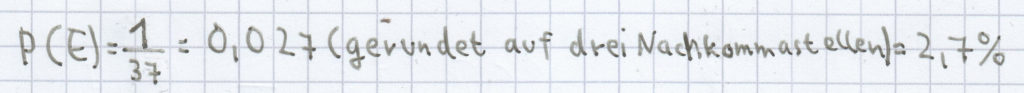
. Deshalb ist die Wahrscheinlichkeit für alle anderen Zahlen als Ergebnis ebenso:

.
Sei es eine Zahl, ein Würfel oder ein Roulette oder etwas anderes, das bei seiner Wahrscheinlichkeit unter das Laplace-Experiment fällt, in der Realität gelten diese Wahrscheinlichkeiten natürlich ebenso! Würde man daher sehr, sehr oft alle Ergebnisse bei einem Münzwurf, bei einem Würfel usw. notieren, dann würden diese sich von der Wahrscheinlichkeit mehr und mehr der durch das Laplace-Experiment berechnenden Wahrscheinlichkeiten annähern.
2.6 Gegenereignis
Liegt ein Ereignis E vor, so kann man auch immer eine eindeutige Aussage über das hierzu gehörige Ereignis Ē, das sogenannte Gegenereignis von E, machen. Das Gegenereignis Ē beinhaltet nämlich immer alle Ergebnisse der Ergebnismenge S eines Zufallsversuches, die nicht zu dem Ereignis E gehören.
Beispiele:
Bei einem einmaligen Münzwurf trat das Ereignis E „Kopf“ ein. Das Gegenereignis Ē ist hier „Zahl“.
Beim dreimaligen Würfeln gab es das Ereignis „Augenzahl 2“ und „Augenzahl 3“. Das Gegenereignis Ē ist hier „Augenzahl 1“, „Augenzahl 4“, „Augenzahl 5“, „Augenzahl 6“.
2.61 Komplementärregel
Liegt ein Ereignis E vor und dessen Ergebnismenge S, so gilt folgende Komplementärregel:
Die Wahrscheinlichkeit P(E) des Ereignisses E und die Wahrscheinlichkeit P(Ē) des hierzu gehörigen Gegenereignisses ergeben zusammen immer 1. Daher gilt hier:
P(E) + P(Ē) = 1
Beispiele:
Bei einem Münzwurf ist die Wahrscheinlichkeit für das Ereignis „Kopf“:
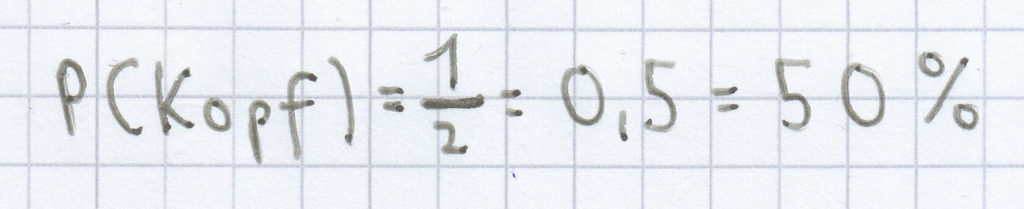
.
Die Wahrscheinlichkeit des Gegenereignisses P(Zahl) ist:
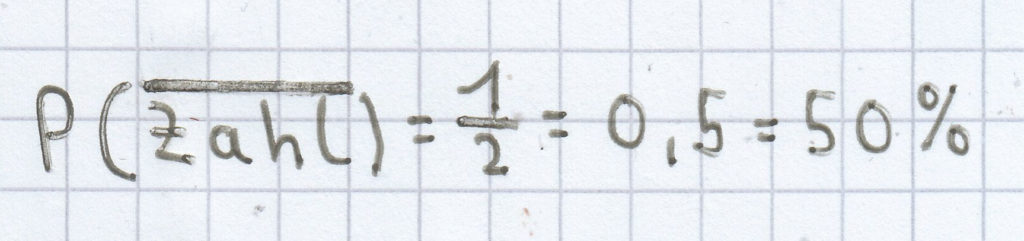
.
P(Kopf) + P (Zahl) = 0,5 + 0,5 = 1.
Die Wahrscheinlichkeit bei einem Würfelwurf, dass das Ereignis „Augenzahl 2“ eintritt ist:
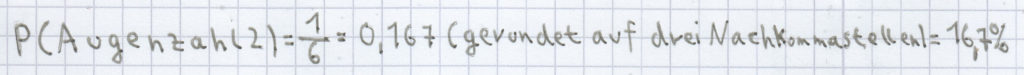
. Die Wahrscheinlichkeit des Gegenereignisses P(Augenzahl 1, 3, 4, 5, 6) ist:
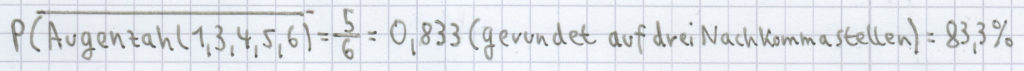
. P(Augenzahl 2) + P(Augenzahl 1, 3, 4, 5, 6) = 0,167 + 0,833 = 1.