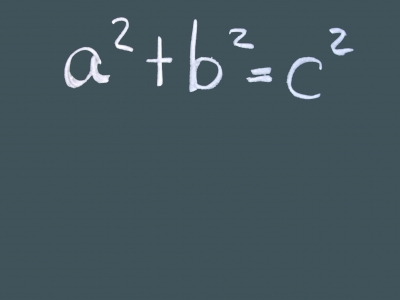Schlagwort: Term

In jedem Raum in einem häuslichen Wohnfeld (es sei denn, man wohnt im Dachgeschoss) begegnet man dem Satz des Pythagoras – und das von Zimmer zu Zimmer gleich doppelt. Normalerweise besitzen ja Räume in Wohnungen eine rechteckige Grundfläche und demzufolge auch die Form eines viereckigen Quaders. Jeder viereckige Quader beziehungsweise Raum enthält nun 2-mal den Satz des Pythagoras – auf der Grundfläche in Form der Flächendiagonalen und im Zimmer selbst in Form der Raumdiagonalen. Hat man daher die Länge und die Breite des Raumes gemessen, dann kann man zunächst über den Satz des Pythagoras die Flächendiagonale des Zimmers berechnen und im Anschluss unter Einbeziehung der Raum-Höhe die Raumdiagonale. Die jeweils ermittelten Ergebnisse lassen dann vielleicht das Zimmer größer erscheinen und man bekommt dadurch eventuell ein positiveres Raumgefühl (das war natürlich eher scherzhaft gemeint 🙂 ).

Eine Gesetzmäßigkeit aus dem Mathematik-Unterricht vergessen viele Menschen ihr Leben lang nicht mehr – den „Satz des Pythagoras“. Der Grund hierfür ist aber bestimmt nicht in einem „mathematischen“ Trauma zu finden, den diese Mathe-Gesetzmäßigkeit bei den einstigen Schülern hervorrief. Denn der Satz des Pythagoras stellt für einen „nicht gerade auf den Kopf gefallenen“ Schüler kein allzu schwieriges Mathe-Stoffgebiet dar. Demzufolge sind irgendwelche psychosomatischen „Folgeschäden“ aufgrund dieser mathematischen Gesetzmäßigkeit auf jeden Fall ausgeschlossen. Vielmehr liegt der Nichtvergessenkönnen-Grund nämlich gerade in der großen Einfachheit und Unkompliziertheit des Satzes begründet. Schließlich muss man sich beim Satz des Pythagoras nur eine überaus einprägsame Gleichung merken – und zwar a² + b² = c².

„Die Probe aufs Exempel machen“, diese Redensart/dieses Sprichwort passt auch bestens zu Gleichungen. Bei jeder Gleichung kann man nämlich mittels des über Äquivalenzumformungen ausfindig gemachten Ergebnisses überprüfen – ob dieses auch wirklich das richtige ist! Hierzu muss man nur einfach stets „die Probe aufs Exempel machen“. Aber wie geht das nun genau bei jeder einzelnen Gleichung? Ganz einfach. Indem man jede ermittelte Lösung in die Ursprungsgleichung einsetzt. Die Ursprungsgleichung ist hierbei immer die Gleichung, an der noch keine Äquivalenzumformungen vorgenommen wurden. „Für mich ist das nicht ganz logisch, da doch eine Lösung eine Lösung ist – und deshalb eigentlich nicht falsch sein kann“, könnte hier jetzt ein „mitdenkender“ Schüler entgegenhalten. Der Mathematik-Lehrer kann zwar den Einwand seines Schülers nachvollziehen, aber trotzdem nichts gegen die Mathe-Tatsache machen, dass nicht jede ermittelte Lösung einer Gleichung auch eine wirkliche Lösung einer Gleichung ist – was demzufolge ebenso der Schüler „schlucken“ muss.

Im Fach Mathematik müssen zum Lösen von Gleichungen fast immer Äquivalenzumformungen angewendet werden. Das sind Umformungen, wobei sich die Lösungsmenge der Ausgangsgleichung nicht ändert. Bei allen Grundrechenarten, „+“, „–“, „·“ und „:“, ist das auf jeden Fall gegeben, wenn hierbei immer nur gleiche Variablen und „nackte“ Zahlen zusammengefasst werden oder die „nackte“ Zahl von der Variable entfernt wird.

Entscheidend bei Äquivalenzumformungen ist nun vor allem, dass jede Äquivalenzumformung einen Schritt näher zur Lösung der Gleichung führen soll. Schließlich tickt in Mathe bei jeder Klassenarbeit und später auch ganz besonders im Abitur stets die Uhr, so dass man eigentlich immer ein Zeitproblem hat, wenn man nicht schnellstmöglich zielgerichtet Aufgaben löst.