1. Allgemeines zu Zahlen
Etwas was jede Schülerin und jeder Schüler vor Beginn des ersten Schuljahres bereits gelernt hat, das sind Zahlen. Im Kindergarten wird einem nämlich bereits die wundersame und wundervolle Welt der Zahlen näher gebracht. Dort lernt man schließlich der Reihe nach die Zahlen von 1 bis 10 – und des Öfteren noch weitere darauffolgende. Daher wird man hier indirekt, ohne es in diesem Alter bewusst zu wissen, schon zweierlei Besonderheiten von Zahlen stets mitlernen bzw. beim Aufsagen beherzigen: das Fortlaufen von Zahlen nach einem bestimmten Abstand und das zunehmende Fortlaufen von Zahlen hin in eine Richtung. Bei den Zahlen 1, 2, 3, 4, 5 usw., die man lernt, ist nämlich der Abstand jeweils gleich groß, nämlich 1, und die Richtung stets im positiven Bereich zunehmend. Schließlich ist die Zahl 2 größer als die Zahl 1 und die Zahl 3 wiederum größer als die Zahl 2 und die Zahl 4 wiederum erneut größer als die Zahl 3 usw.

1.1 Veranschaulichung von Zahlen an einer Zahlengeraden
In der Grundschule in Mathe wird man dann noch eine weitere wichtige Zahl dazu lernen, die Zahl Null. Dort lernt man nämlich dann, dass die bereits gelernten Zahlen 1, 2, 3, 4, 5 usw. bei der Zahl 0 beginnen. Veranschaulicht wird das in der Mathematik an einer sogenannten Zahlengeraden. Das ist ein waagrechter Strich, an dem senkrecht jeweils in gleichmäßigem Abstand kleinere Striche mit den fortlaufenden Zahlen gemacht werden und an dessem rechten Ende ein Pfeil sich befindet. Hierdurch kommt zum Ausdruck, dass die Zahlen in diese Richtung unendlich fortsetzbar sind (was übrigens in die andere Richtung der Zahlengeraden ebenso gilt!).
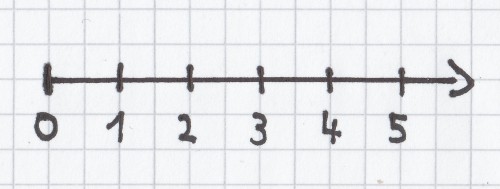
1.2 Dezimales Stellenwertsystem
Zahlen zu bestimmen, muss man lernen. Denn bspw. eine 4 bedeutet nicht immer eine 4.
Wenn man sich die Zahlen 4, 41, 410 anschaut, dann hat die Ziffer 4 hier jeweils einen unterschiedlichen Wert.
Je nach Position bei der Zahl hängt hierbei ihr Wert ab.
Bei 4 gibt es nur eine Ziffer, also nur 1er. Daher ist hier ihr Wert 4, gesproche vier. Bei 41 gibt es zwei Ziffern, wobei hier die Zahl aus 10ern und 1ern besteht. Da die 4 hier an erster Stelle steht, hat diese den Wert 40 und die Zahl lautet gesprochen: einundvierzig. Bei der Zahl 410, die drei Ziffern vorweist und die Zahl somit aus 100ern, 10ern und 1ern besteht, steht die 4 wiederum an der ersten Stelle. Jetzt hat sie aber den Wert 400 bzw. gesprochen: vier Hundert.
Den Zahlen, wie wir sie lernen, liegt ein sogenanntes Stellenwertsystem zugrunde. Das heißt nichts anderes als: Je nach Stelle bei einer Zahl bestimmt sich deren Wert.
Merkmale eines Stellenwertsystems
1. Anhand des Stellenwertsystems wird deutlich, welche Anzahl und Position von Bündelungseinheiten, 1ern, 10ern, 100ern usw., bei einer bestimmten Zahl vorliegt.
2. Bei einem Stellenwertsystem wird zwischen den Begriffen Ziffer, Stelle einer Ziffer und dem Wert, der von der Stelle der Ziffer abhängt, unterschieden.
3. Die Anzahl der zur Verfügung stehenden Ziffern nennt man Basis des Stellenwertsystems.
Das dezimale Stellenwertsystem verwendet diese zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Die Basis des dezimalen Stellenwertsystems (lateinisch decem für zehn): ist zehn.
Die Bündelungseinheiten werden durch Potenzen der Zahl 10 wiedergegeben und bezeichnen die Stelle im dezimalen Stellenwertsystem.
100 = 1, bezeichnet die 1er Stelle
101 = 10, bezeichnet die 10er Stelle
102 = 100, bezeichnet die 100er Stelle
103 = 1000, bezeichnet die 1000er Stelle
usw.
Es wird bei einem dezimalen Stellenwertsystem zwischen Stellenwert und Zahlenwert einer Ziffer unterschieden.
Je nach Stellung der Ziffer innerhalb einer Zahl ergibt sich die jeweilige Bündelungseinheit (1er, 10, 100er, 1000er, usw.). Das nennt man den Stellenwert einer Ziffer.
Bei jeder Ziffer kann man zusätzlich erkennen, wie viele Bündelungseinheiten (1er, 10, 100er, 1000er, usw.) vorliegen. Das nennt man den Zahlenwert einer Ziffer.
Wie erklärt sich die Zahl 5429 anhand des dezimalen Stellenwertsystems?
Man kann diese Schritt für Schritt mittels Potenzen, genauer gesagt als Zehnerpotenzen, wiedergeben, in Abhängigkeit vom Stellenwert und Zahlenwert der Zahl.
Die 1000er bzw. 5000 kann man mit 5 · 103 wiedergeben (von rechts vierte Stelle beinhaltet 1000er mit hier dem Zahlenwert 5, also der 5-Fachen 1000er Bündelung).
Die 100er bzw. 400 kann man mit 4 · 102 wiedergeben (von rechts dritte Stelle beinhaltet 100er mit hier dem Zahlenwert 4, also der 4-Fachen 1000er Bündelung).
Die 10er kann bzw. 20 man mit 2 · 102 wiedergeben (von rechts zweite Stelle beinhaltet 10er mit hier dem Zahlenwert 2, also der 2-Fachen 10er Bündelung).
Die 1er bzw. 9 kann man mit 9 · 100 wiedergeben (von rechts erste Stelle beinhaltet 1er mit hier dem Zahlenwert 9, alos der 9-Fachen 1er Bündelung).
Die Zahl 5429 setzt sich je nach Stellenwert und Zahlenwert aus Potenzen also folgendermaßen zusammen:
5429 = 5 ·103 + 4 ·102 + 2 · 102 + 9 · 100.
1.3 Stellenwerttafel
Folgende Zahlen sind gegeben:
12, 534, 51749, 419900, 57800333, 1275600889, 375840780905568.
Gib diese Zahlen als Zehnerpotenzen wieder und trage diese anschließend in eine Stellenwerttafel ein.
12 = 1 · 101 + 2 · 100,
532 = 5 · 102 + 3 · 101 + 2 · 100,
419900 = 4 · 105 + 1 · 104 + 9 · 103 + 9 · 102 + 0 · 101 + 0 · 100,
57800333 = 5 · 107 + 7 · 106 + 8 · 105 + 0 · 104 + 0 · 103 + 3 · 102 + 3 · 101 + 3 · 100,
1275600889 = 1 · 1010 + 2 · 109 + 7 · 108 + 5 · 107 + 6 · 106+ 6 · 105 + 0 · 104 + 0 · 103 + 8 · 102 + 8 · 101+ 9 · 100,
375840780905568 = 3 · 1014 + 7 · 1013 + 5 · 1012 + 8 · 1011 + 4 · 1010 + 0 · 109 + 7 · 108+ 8 · 107 + 0 · 106+ 9 · 105 + 0 · 104 + 5 · 103 + 5 · 102 + 6 · 101 + 8 · 100

Die Stellenwerttafel fängt von rechts mit der kleinsten Zehnerpotenz an und nimmt nach rechts immer um eine Zehnerpotenz zu.
Die Bündelungenseinheiten sind hierbei folgende:
100 = Einer (Abkürzung in der Stellenwerttafel oft auch „E“)
101 = Zehner (Abkürzung in der Stellenwerttafel oft auch „Z“)
102 = Hunderter (Abkürzung in der Stellenwerttafel oft auch „H“)
103 = Tausender (Abkürzung in der Stellenwerttafel oft auch „T“
104 = Zehntausender (Abkürzung in der Stellenwerttafel oft auch „ZT“)
105 = Hunderttausender (Abkürzung in der Stellenwerttafel oft auch „HT“)
106 = Millionen (Abkürzung in der Stellenwertafel oft auch „MIO“)
107 = Zehnmillionen (Abkürzung in der Stellenwettaffel oft auch „ZMIO“
108 = Hundertmillionen (Abkürzung in der Stellenwerttafel oft auch „HMIO“)
109 = Milliarden (Abkürzung in der Stellenwerttafel oft auch „MRD“)
109 = Zehnmilliarden (Abkürzung in der Stellenwerttafel oft auch „ZMRD“
109 = Hundermilliarden (Abkürzung in der Stellenwerttafel oft auch „HMRD“
109 = Billionen (Abkürzung in der Stellenwerttafel oft auch „BIO“
109 = Zehnbillionen (Abkürzung in der Stellenwerttafel oft auch „ZBIO“
109 = Hunderbillionen (Abkürzung in der Stellenwerttafel oft auch„HBIO“