Oberfläche und Volumen von Pyramiden sind Teil der Raumgeometrie. Wie aber berechnet man das Volumen und die Oberfläche von Pyramiden am unkompliziertesten? Welche Formeln benötigt man dazu und an welcher Stelle muss man mit dem Satz des Pythagoras rechnen? Eine Reihe von Fragen also, die wir im Folgenden beantworten wollen. Ein spezielles Augenmerk dabei werden wir auf die häufigsten Fehler legen, die Schülern in Klassenarbeiten immer wieder unterlaufen und mit welchen Strategien man sie am besten verhindern kann. Sehen wir uns zunächst einmal zwei Pyramiden an:
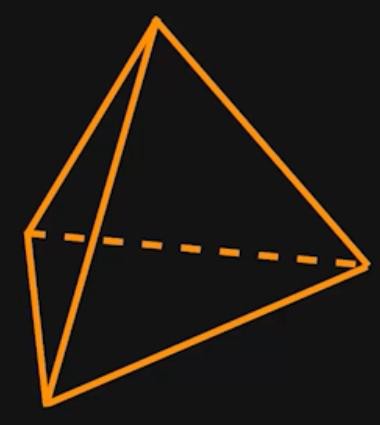
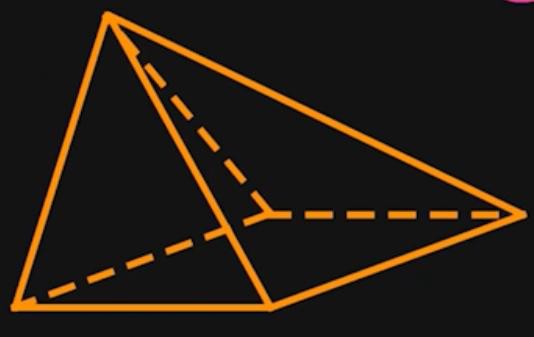
Wie wir erkennen, ist eine Pyramide ein Körper, der aus einer Grundfläche und Seitenflächen besteht. Die Grundfläche einer Pyramide kann wie in unseren Beispielen ein Dreieck oder ein Rechteck sein, es sind aber auch Quadrate und andere Vielecke als Grundfläche einer Pyramide denkbar. Die Anzahle der Ecken der Grundfläche bestimmt dabei die Anzahl der Seitenflächen. So hat eine Pyramide mit einem Dreieck als Grundfläche auch drei Seitenflächen.
Die Seitenflächen einer Pyramide sind immer Dreiecke, die an der Spitze der Pyramide zusammenlaufen. Das Lot von der Spitze der Pyramide auf die Grundfläche ist die Höhe des Körpers.
Nun aber erstmal genug der Theorie. Sehen wir uns nun der Reihe nach an, wie wir das Volumen und die Oberfläche einer Pyramide berechnen.
Volumen der Pyramide:
Wir haben festgestellt, dass eine Pyramide ein spitzer Körper ist. Mit diesem Wissen können wir für alle Pyramiden allgemein folgende Grundformel aufstellen:
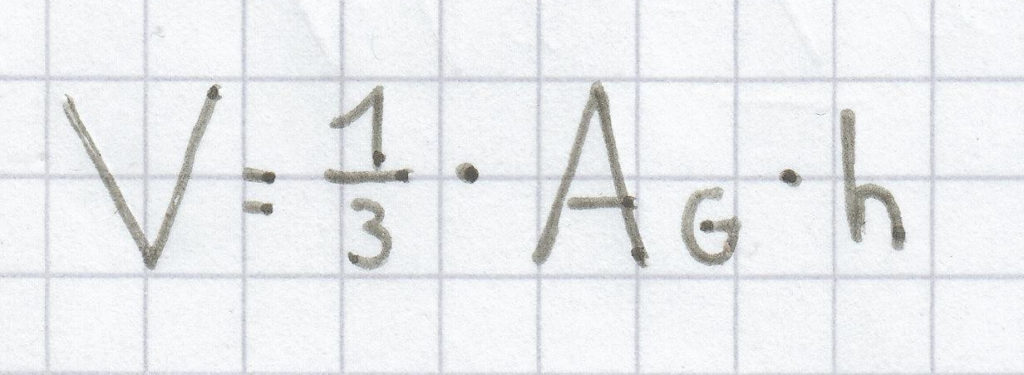
Wir berechnen also die Grundfläche AG nehmen diese mal der Höhe der Pyramide und teilen das Ergebnis durch 3, da eine Pyramide ein spitzer Körper ist.
Mehr lässt sich theoretisch dazu auch gar nicht sagen. Gehen wir deswegen gleich in die Praxis und sehen uns die hauptsächliche Fehlerquelle bei der Volumenberechnung an.
Welche Höhe ist richtig?
Die wichtigste Fehlerquelle beim Volumen von Pyramiden ist, die Höhe der Pyramide richtig zu verwenden. Eine Pyramide hat zwar eigentlich nur eine Höhe, jedoch haben auch die Dreiecke, die die Seitenflächen der Pyramide sind, natürlich eine eigene Höhe. Diese Höhe ist aber nicht richtig, um damit das Volumen zu berechnen. Hier benötigen wir, und das vergessen Schüler gerne, den Lehrsatz des Pythagoras, nämlich a2 + b2 = c2. In der folgenden Skizze ist das Problem anschaulich dargestellt:
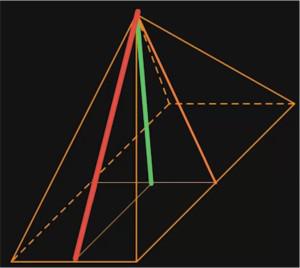
Die rote Linie ist eine der Seitenhöhen und die grüne Linie ist die Höhe der Pyramide. Die grüne Linie und die rote Linie bilden mit dem Teil der Grundlinie ein rechtwinkliges Dreieck, wobei die rote Linie, also die Seitenhöhe die Hypothenuse ist. Wenn du die Körperhöhe nicht gegeben hast, aber die rote Seitenhöhe, kannst du sie mit dem Satz des Pythagoras berechnen.
Wenn du die Körperhöhe hast, dann brauchst du nur noch in die Formel zur Volumenberechnung einsetzen.
Mein Tipp: Um zu vermeiden, dass du die falsche Höhe zur Berechnung verwendest, solltest du dir immer eine Skizze nach den Angaben machen und sorgfältig die gegebenen Größen eintragen.
Oberfläche der Pyramide:
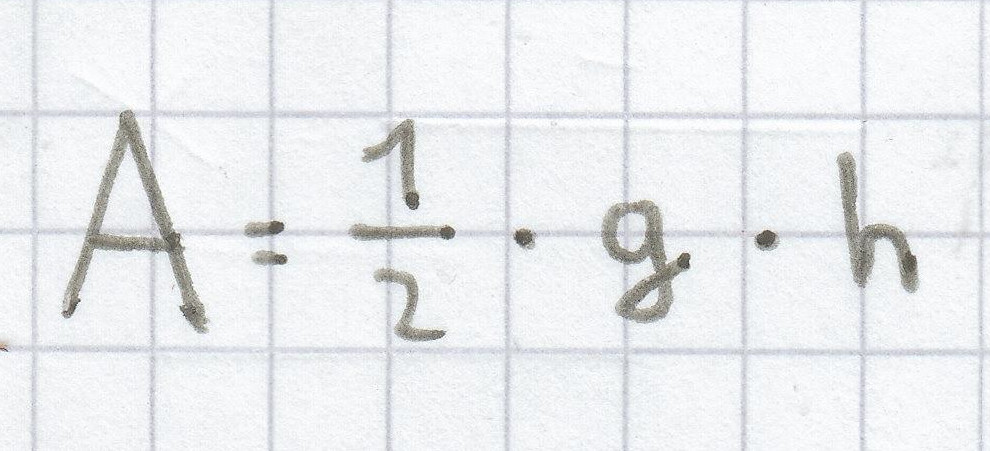
Die Oberfläche einer Pyramide besteht aus der Grundfläche und der sogenannten Mantelfläche. Die Mantelfläche ist die Summe aller Dreiecke, die die Pyramide als Seitenflächen hat. Schau dir als Gedächtnisstütze einfach nochmal die beiden Skizzen vom Anfang des Textes an.
Du musst also zuerst die Grundfläche mit der dafür zuständigen Formel berechnen und dann die unterschiedlichen Seitenflächen. Diese sind immer Dreiecke und dafür ist folgende Formel, wie wir wissen zuständig:
Soweit zur Theorie. Auch die Berechnung der Oberfläche wartet mit einer Fehlerquelle auf und zwar der Gleichen wie die Berechnung des Volumens.
Welche Höhe ist richtig?
Sehen wir uns noch einmal die Skizze von oben an. Zur Übersichtlichkeit habe ich sie hier noch einmal abgebildet:
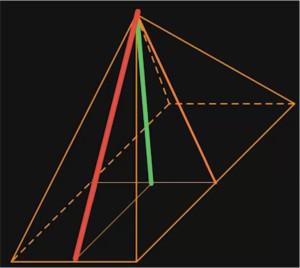
Zur Berechnung der Oberfläche brauchen wir die Fläche des Dreiecks, indem die rote Linie eingezeichnet ist. Das ist nämlich die Höhe, die auch als „h“ in der Flächenformel für Dreiecke enthalten ist. Diese rote Linie ist aber in manchen Aufgaben nicht angegeben und du darfst dann nicht den Fehler machen, dass du mit der Körperhöhe (grüne Linie) versuchst, das Seitendreieck zu berechnen, nur weil sie gegeben ist.
Wenn du die Seitenhöhe eines Dreiecks nicht gegeben hast, aber die Körperhöhe, dann kannst du sie über den Satz des Pythagoras (a2 + b2 = c2) berechnen. Die Seitenhöhe und die Körperhöhe bilden nämlich mit dem Stück der Grundlinie ein rechtwinkliges Dreieck. Hierbei ist die Seitenhöhe des Dreiecks immer die Hypotenuse.
Mein Tipp: Mach dir wie für die Volumenberechnung eine saubere Skizze und beschrifte sie ordentlich, dann kommst du nicht in die Gefahr, die falsche Höhe zu verwenden.

Zusammenfassende Tipps zur Berechnung von Volumen und Oberfläche einer Pyramide:
- Skizze anfertigen!
Solltest du in einer Schulaufgabe oder Klassenarbeit eine Angabe vorfinden, die nur aus Worten besteht kannst du nur mit einer ordentlichen Skizze sicherstellen, dass du auch alle Angaben richtig verstanden hast und sie dann richtig anwenden! - Skizze genau ansehen!
Welche Maßeinheiten hast du gegeben? Sind diese in der gleichen Maßeinheit? Bitte nicht Äpfel mit Birnen vergleichen!
Welche Flächen hast du gegeben?
Welche Höhe hast du gegeben und welche brauchst du? Musst du den Satz des Pythagoras anwenden? - Welche Formeln musst du anwenden?
Überlege dir das vorher, damit du entscheiden kannst, ob du alle Maße gegeben hast, oder ob du noch etwas berechnen musst, bevor du Oberfläche und Volumen berechnen kannst! - Rechne Schritt für Schritt! Mache nicht zu viele Schritte auf einmal, sonst besteht die Gefahr, dass du durcheinander kommst.
- Überprüfe dein Ergebnis! Vergleiche die Maßeinheit des Ergebnisses mit der der Angaben und der Skizze! Nur so kannst du entscheiden, ob du ein sinnvolles Ergebnis erhalten hast!
Zu meiner Person:
Ich betreibe den Blog „der-nachhilfe-lehrer.de“ ( https://der-nachhilfe-lehrer.de/ ) und bin seit über zwanzig Jahren in der professionellen Schülernachhilfe tätig. Der Inhalt meines Blogs besteht hauptsächlich aus verständlichen aber auch thematisch umfassenden Erklär-Texten zu wichtigen Stoffgebieten der Schule. Mein Schwerpunkt liegt darauf, den Schulstoff so zu erklären, dass sich die Schüler da abgeholt fühlen, wo sie sind, nämlich entweder direkt nach der Neueinführung eines Stoffgebietes in der Schule oder kurz vor einer Klassenarbeit. Durch eine für Schüler verständliche Sprache möchte ich ihnen die „Angst“ vor dem Stoff nehm