
Proportional ist ein sehr wichtiges Wort in der Mathematik. Vielen Aufgaben in Mathe liegen nämlich sogenannte proportionale Zuordnungen zugrunde. Was bedeutet aber das Wort proportional genau? Am einfachsten kann man sich das mittels eines Vergleichs vor Augen führen, zum Beispiel bei einem Produkt aus dem Supermarkt. 6 Bio-Eier (natürlich Freilandhaltung) kosten dort beispielsweise 2,10 €. 12 Bio-Eier kosten dann – 4,20 € (also doppelt so viel). Es liegt schließlich eine proportionale Zuordnung vor, d. h. die zugeordneten Größen (hier Bio-Eier → Preis) stehen in einem gleichen Verhältnis zueinander. Das ist sehr praktisch. So kann man schließlich über den sogenannten Dreisatz, der auf proportionalen Zuordnungen fußt, jegliche beliebe Zuordnung berechnen – wie beispielsweise 1 Bio-Ei kostet (wenn man es einzeln im Supermarkt kaufen könnte) oder 105 usw.
Aufgaben zum Mathe-Stoffgebiet Dreisatz
1. Mathematik-Nachhilfe-Aufgabe: Vervollständige die Zuordnung Benzinvolumen → Preis.
Benzinvolumen Preis
36 l 28,08 €
13 l 10,14 €
49 l __
7 l __
__ 32,76 €
23 l __
26 l __
35 l __
2. Mathematik-Nachhilfe-Aufgabe: Ein Fischfilet mit einem Gewicht von 300 g kostet 8 Euro.
a) Zeichne die proportionale Zuordnung Gewicht Fisch → Preis in ein Koordinatensystem ein.
b) Der Fisch kostet nach einer Preiserhöhung nun wie folgt: 300 g → 8,50 €. Zeichne ebenfalls die proportionale Zuordnung in dasselbe Koordinatensystem ein. Was fällt auf?
c) In einem anderen Supermarkt ist der Fisch günstiger. 300 g kosten 7,50 €. Zeichne ebenfalls den Graphen in das vorhandene Koordinatensystem. Was fällt auf?
3. Mathe-Nachhilfe-Aufgabe: Im Sommer dehnt sich während sehr warmer Sommertage das Eisen bei Eisenbahnschienen oft aus. So etwa eine Streckenlänge von 20 m um 8 cm. Wie stark ist die Ausdehnung bei 40 m; 60 m; 30 m und 90 m Streckenlänge?
4. Mathematik-Nachhilfe-Aufgabe: Ein Stoff für Vorhänge kostet wie folgt: 1 m → 18,40 €. Berechne wie viel 0,6 m; 3,8 m; 7,6 m und 8,5 m desselben Stoffes kosten.

Lösungen zum Mathematik-Stoffgebiet Dreisatz
1. Mathe-Nachhilfe-Aufgabe: Es soll folgende Zuordnung Benzinvolumen → Preis vervollständigt werden.
Benzinvolumen Preis
36 l 28,08 €
13 l 10,14 €
49 l __
7 l __
__ 32,76 €
23 l __
26 l __
35 l __
Hier muss man nun genau gucken, welche Größen man mittels einer Multiplikation oder einer Division berechnen kann. Da eine proportionale Zuordnung vorliegt, muss die getätigte Rechenoperation, ein Multiplizieren oder ein Dividieren, natürlich immer auf beiden Seiten der Zuordnung durchgeführt werden.
Ganz einfach kann man hier durch eine Multiplikation den fehlenden Wert berechnen:
13 l 10,14 € | · 2
26 l 20,28 €
Um die anderen fehlenden Werte ganz einfach berechnen zu können, berechnet man nun bei einer Zuordnung den Preis für 1 l Benzinvolumen.
36 l 28,08 € | : 36
1 l 0,78 €
Hierauf kann man nun alle anderen fehlenden Benzinvolumenwerte-Werte berechnen.
1 l 0,78 € | · 49
49 l 38,22 € | : 7
7 l 5,46 € | · 5
35 l 27,30 €
1 l 0,78 € | · 23
23 l 17,94 €
Bei dem fehlenden Liter-Wert sollte man ein paar Mal ausprobieren, welcher Euro-Wert mittels Multiplikation den angegeben Euro-Wert ergibt. Das kann man ganz einfach, indem man den gegeben Wert 32,76 € durch ein paar andere Euro-Werte teilt. Bei geteilt durch 5,46 € ergibt sich hierbei beispielsweise genau 6. Man kann aber auch ganz einfach einen Dreisatz anwenden, wie beispielsweise so: (7 l · 32,76 €) : 5,46 € = 42 l. Beim Dreisatz nimmt man immer zwei Werte über Kreuz mal und teilt den dritten Wert durch das Produkt. Das Ergebnis liefert den fehlenden Wert.
7 l 5,46 € | · 6
42 l 32,76 €
Die vollständige Zuordnung Benzinvolumen → Preis sieht dann wie folgt aus:
Benzinvolumen Preis
36 l 28,08 €
13 l 10,14 €
49 l 38,22 €
7 l 5,46 €
42 l 32,76 €
23 l 17,94 €
26 l 20,28 €
35 l 27,30 €
2. Mathe-Nachhilfe-Aufgabe: Es kostet ein Fischfilet mit einem Gewicht von 300 g 8 Euro.
a) Die proportionale Zuordnung Gewicht des Fisches → Preis soll in ein Koordinatensystem gezeichnet werden.
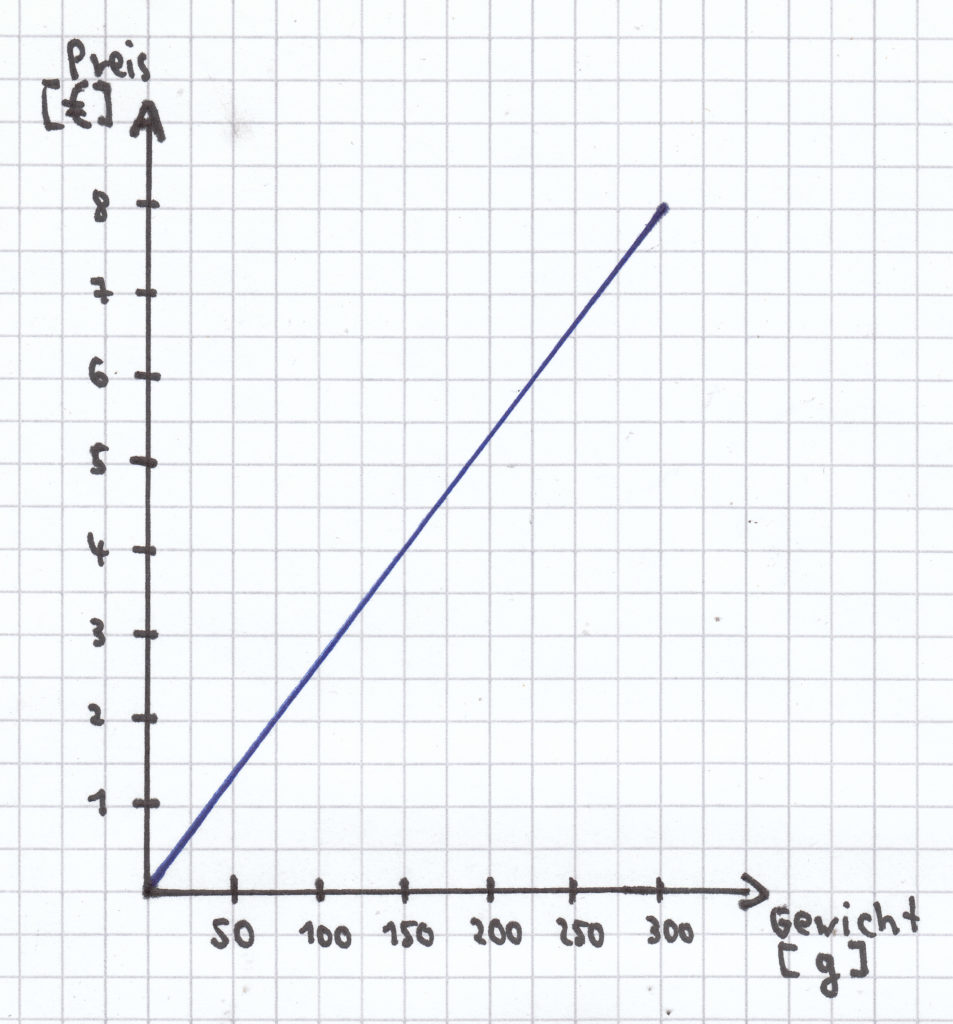
b) Nach einer Preiserhöhung kostet der Fisch nun folgendermaßen: 300 g → 8,50 €. Diese Zuordnung soll ebenfalls in das gleiche Koordinatensystem eingezeichnet werden. Was fällt hierbei auf?
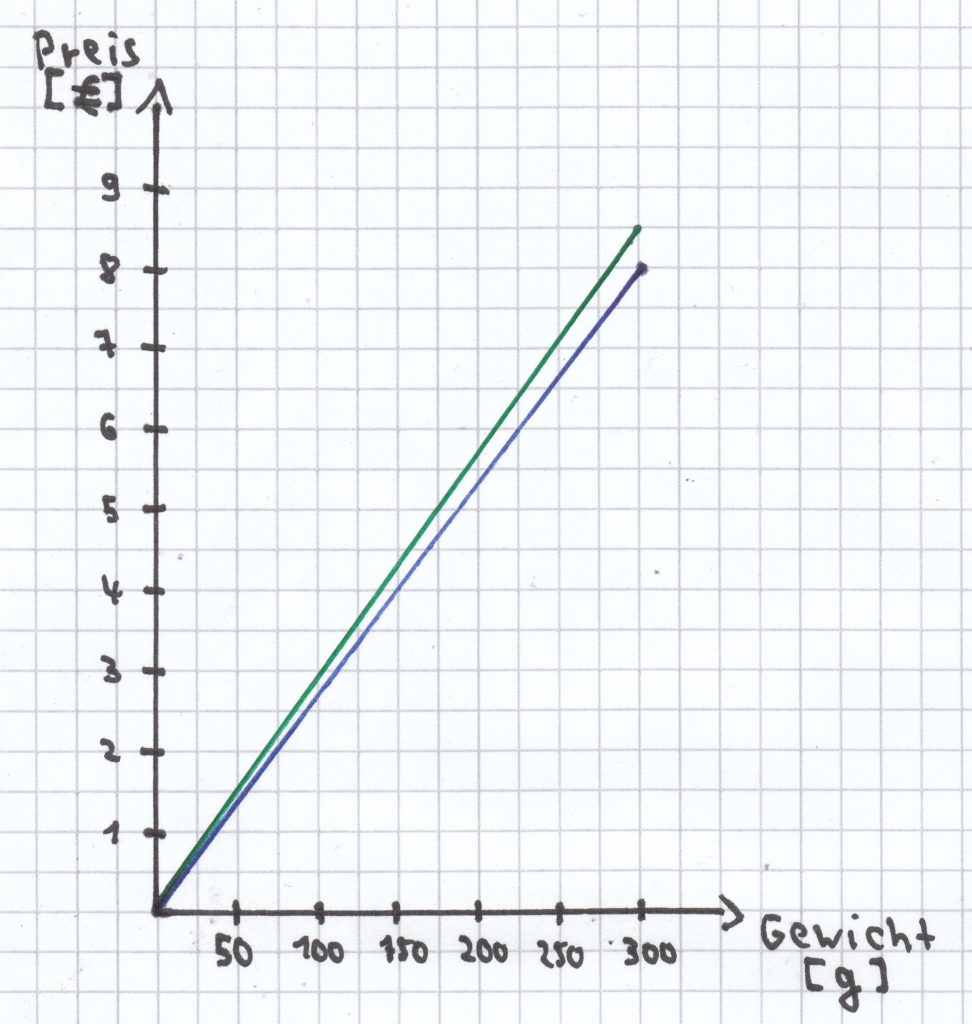
Es fällt auf, dass die grüne (Halb-)Gerade steiler verläuft als die blaue (Halb-)Gerade. Denn der eine Preis (grün) des Fischfilets ist teurer als der andere Preis (grün).
c) Auf einem Fischmarkt kosten 300 g Fischfilet 7,50 €. Der Graph dieser Zuordnung soll ebenso ins Koordinatensystem eingezeichnet werden. Was fällt hier wiederum auf?
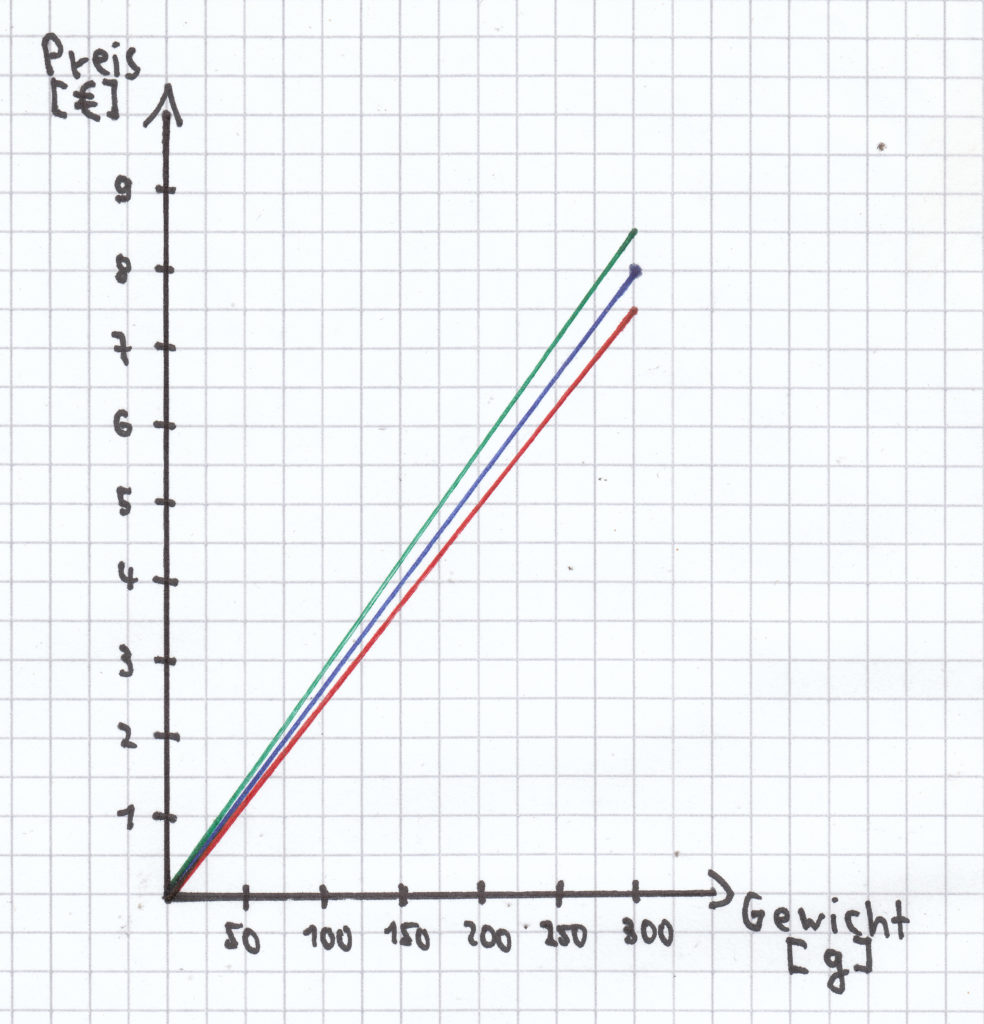
Der günstigste Preis für das Fischfilet, die rote (Halb-)Gerade, verläuft flacher als die anderen beiden. Der teuerste Preis, die grüne (Halb-)Gerade, verläuft am steilsten. Der Preis, der zwischen diesen beiden liegt, ist die blaue (Halb-)Gerade in der Mitte.
3. Mathematik-Nachhilfe-Aufgabe: Wenn es Sommer ist, dann dehnt sich am warmen Sommertagen das Eisen von Eisenbahnschienen aus. Bei einer Streckenlänge von 20 m etwa um 8 cm. Berechne die Ausdehnung bei einer Streckenlänge von 40 m; 60 m; 30 m und 90 m.
20 m 8 cm | · 2
40 m 16 cm
20 m 8 cm | · 3
60 m 24 cm | : 2
30 m 12 cm | · 3
90 m 36 cm
Bei 40 m beträgt die Ausdehnung der Schienen, 16 cm; bei 60 m 24 cm; bei 30 m 12 cm und bei 90 m 36 cm.
4. Mathe-Nachhilfe-Aufgabe: In einem Geschäft kostet der Stoff für Vorhänge wie folgt: 1 m → 18,40 €. Ermittle den Preis für 0,6 m; 3,8 m; 7,6 m und 8,5 m an Stoff.
1 m 18,40 € | · 0,6
0,6 m 11,04 €
1 m 18,40 € | · 3,8
3,8 m 69,92 € | · 2
7,6 m 139,84 €
1 m 18,40 € | · 8,5
8,5 m 156,40 €
Im Geschäft kosten 0,6 m Stoff für Vorhänge 11,04 €; 3,8 m 69,92 €; 7,6 m 139,84 € und 8,5 m 156,40 €.