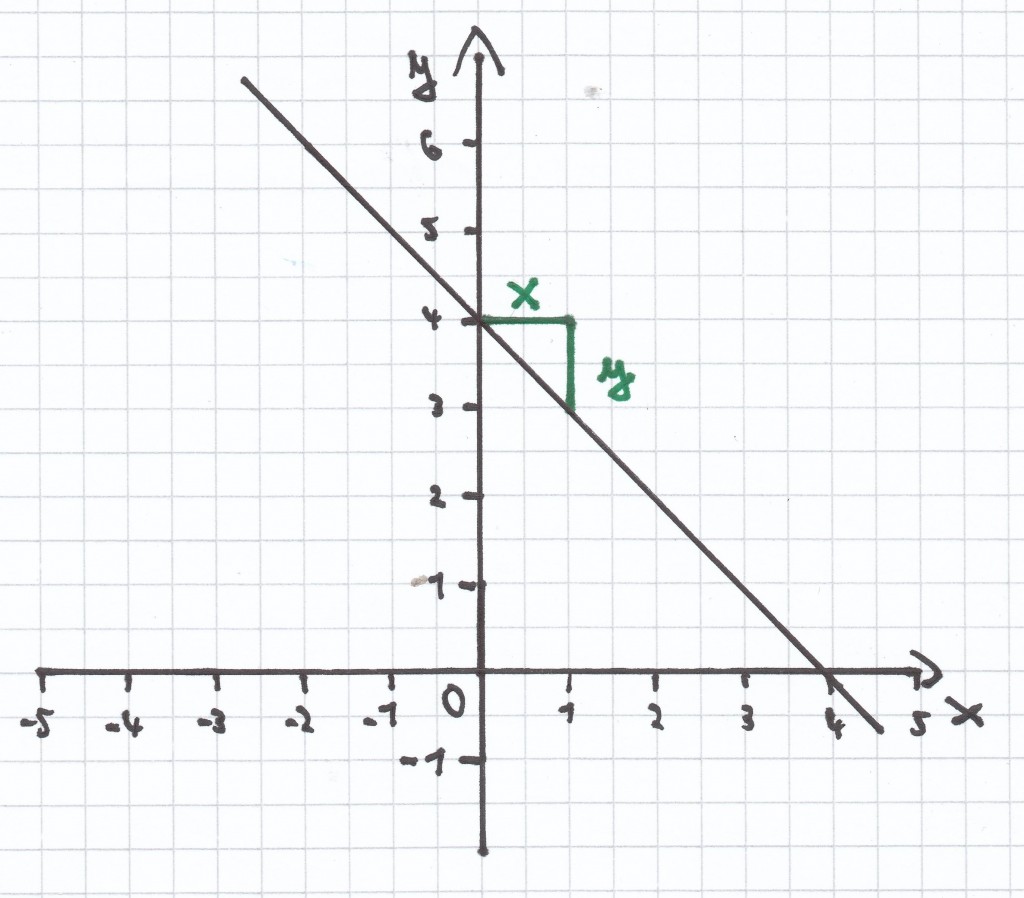
Die ersten in Mathe dran kommenden Funktionen sind lineare Funktionen.
Diese haben folgende Zuordnungsvorschrift:
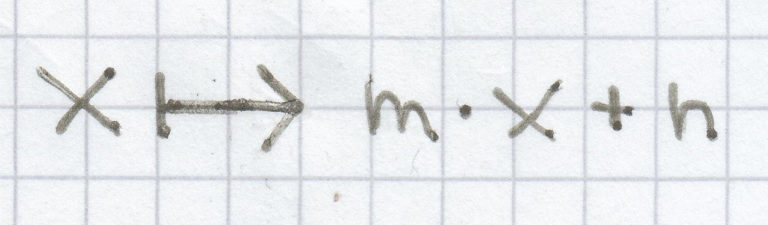
und diese Funktionsgleichung:
y = m · x + n.
Wie man sieht, weisen lineare Funktionen in der Regel eine Variable/„x“ auf, die die Potenz hoch eins/„x“ bzw. „x¹“ besitzt. Darüber hinaus einen konstanten Wert/„m“, der mit der Variablen verbunden ist. „m“ ist hierbei die Steigung der linearen Funktion. Ebenso besitzen lineare Funktionen oftmals einen zweiten konstanten Wert, nämlich „n“. „n“ wird hierbei als das absolut Glied bezeichnet und ist der Ordinatenabschnitt, also der Schnittpunkt mit der y-Achse. Hat man die Funktionsgleichung einer linearen Funktion gegeben, so kann man diese immer sofort in ein Koordinatensystem einzeichnen. Der Graph der so dargestellten linearen Funktion ist hierbei immer eine Gerade.
Aufgaben zum Mathematik-Stoffgebiet Lineare Funktionen
1. Mathe-Nachhilfe-Aufgabe: Mache die Punktprobe! Überprüfe welche Punkte zur linearen Funktion gehören. Folgende Punkte sind gegeben:
P1 (1|4), P2 (2|3), P3 (2|1), P4 (4|2), P5 (–8|10), P6 (–2|–1).
a) 3y + 2x = 14
b) –3y + 5x = –7
c) ${\frac{y}{2}$ – ${\frac{x}{4}$ = 0
2. Mathematik-Nachhilfe-Aufgabe: Gib die Steigung der linearen Funktion an. Ermittle ebenso den Schnittpunkt mit der y-Achse und den Schnittpunkt mit der x-Achse.
a) 4x + 5y = 5
b) –3y + x = 0
c) 3y = 12x + 15
d) ${\frac{y}{4}$ + ${\frac{x}{2}$ – ${\frac{3}{4}$ = 0
3. Mathe-Nachhilfe-Aufgabe: Ergänze folgende Punkt so, dass diese jeweils auf den gegeben linearen Funktionen liegen:
P1 (_|0), P2 (0|_), P3 (_|6), P4 (1|_), P5 (_|–0,6), P6 (–0,2|_).
a) 2x – 5y = 0
b) y + x = 1
c) 0,4y – 1,2x = 4,8
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2
4. Mathe-Nachhilfe-Aufgabe: Es sind zwei Variablen gegeben. Löse zunächst die Gleichung nach der Variablen y hin auf und zeichne anschließend die Funktion.
a) 3x – 5y = 20
b) 2y + 4x = 20
c) y + ${\frac{x}{2}$ = –3,5
d) ${\frac{v~+~y}{4}$ = 1
Lösungen zum Mathe-Stoffgebiet Lineare Funktionen
1. Mathematik-Nachhilfe-Aufgabe: Mache bei den linearen Funktionen die Punktprobe und überprüfe, ob folgende Punkte zu der Funktion gehören:
P1 (1|4), P2 (2|3), P3 (2|1), P4 (4|2), P5 (–8|10), P6 (–2|–1).
Ein Punkt ist immer zu einer Funktion, egal welcher, gehörend, wenn der x-Wert und y-Wert des Punktes eingesetzt in die Funktion eine wahre Aussage ergibt. Jeder Punkt hat hat einen x-Wert (der erste Wert) und einen y-Wert (der zweite Wert). Eine Funktion weist ebenso immer auch einen x-Wert und einen y-Wert auf. Setzt man nun die Werte des Punktes in die Funktionsgleichung ein und die Funktionsgleichung liefert eine wahre Aussage, so liegt der Punkt auf der Funktion. Dadurch ergibt sich auch diese Umkehrung: Ist das jedoch nicht der Fall, dass die Funktionsgleichung eine wahre Aussage liefert, so gehört der Punkt nicht zu der Funktion.
a) 3y + 2x = 14
P1 (1|4)
3 · (4) + 2 · (1) = 14 <=>
12 + 2 = 14 <=>
14 = 14
Die Gleichung liefert eine wahre Aussage. Der Punkt P1 (1|4) liegt daher auf der Funktion.
P2 (2|3)
3 · (3) + 2 · (2) = 14 <=>
9 + 4 = 14 <=>
13 = 14
Da die Gleichung keine wahre Aussage liefert, liegt der Punkt P2 (2|3) nicht auf der Funktion.
P3 (2|1)
3 · (1) + 2 · (2) = 14 <=>
3 + 4 = 14 <=>
7 = 14
Der eingesetzte Punkt P3 (2|1) gehört nicht zu der Funktion, da dieser eingesetzt keine wahre Aussage ergibt.
P4 (4|2)
3 · (2) + 2 · (4) = 14 <=>
6 + 8 = 14 <=>
14 = 14 <=>
Da der eingesetzte Punkt P4 (4|2) eine wahre Aussage der Gleichung liefert, liegt er auf der linearen Funktion.
P5 (-8|10)
3 · (10) + 2 · (–8) = 14 <=>
30 – 16 = 14 <=>
14 = 14 <=>
Die Punktprobe belegt, dass der Punkt P5 (-8|10) auf der Funktion liegt.
P6 (–2|–1)
3 · (–1) + 2 · (–2) = 14 <=>
–3 – 4 = 14 <=>
–7 = 14
Da die Gleichung eine unwahre Aussage ergibt, liegt der Punkt P6 (–2|–1) nicht auf der Funktion.
b) –3y + 5x = –7
P1 (1|4)
–3 · (4) + 5 · (1) = –7 <=>
–12 + 5 = 7 <=>
–7 = –7 <=>
Die Gleichung liefert eine wahre Aussage. Demzufolge gehört der Punkt P1 (1|4) zu der linearen Funktion.
P2 (2|3)
–3 · (3) + 5 · (2) = –7 <=>
–9 + 10 = –7 <=>
1 = –7
Der Punkt P2 (2|3) liegt nicht auf der Funktion, da die Gleichung eine unwahre Aussage ergibt.
P3 (2|1)
–3 · (1) + 5 · (2) = –7 <=>
–3 + 10 = –7 <=>
7 = –7
Die Aussage ist unwahr. Daher ist der Punkt P3 (2|1) nicht zu der Funktion gehörend.
P4 (4|2)
–3 · (2) + 5 · (4) = –7 <=>
–6 + 20 = –7 <=>
14 = –7
Die Gleichung liefert eine unwahre Aussage. Der Punkt P4 (4|2) liegt daher nicht auf der Funktion.
P5 (–8|10)
–3 · (10) + 5 · (–8) = –7 <=>
–30 – 40 = –7 <=>
–70 = –7
Da die Gleichung keine wahre Aussage ergibt, liegt der Punkt P5 (–8|10) nicht auf der Funktion.
P6 (–2|–1)
–3 · (–1) + 5 · (–2) = –7 <=>
3 – 10 = –7 <=>
–7 = –7
Die Aussage liefert eine wahre Aussage. Der Punkt P6 (–2|–1) gehört daher zu der Funktion.
c) ${\frac{y}{2}$ – ${\frac{x}{4}$ = 0
P1 (1|4)
${\frac{4}{2}$ – ${\frac{1}{4}$ = 0 <=>
2 – 0,25 = 0 <=>
1,75 = 0
Die Gleichung ergibt eine unwahre Aussage. Daher gehört der Punkt P1 (1|4) nicht zu der linearen Funktion.
P2 (2|3)
${\frac{3}{2}$ – ${\frac{2}{4}$ = 0 <=>
1,5 – 0,5 = 0 <=>
1 = 0
Da der Punkt P2 (2|3) keine wahre Aussage ergibt, liegt dieser nicht auf der Funktion.
P3 (2|1)
${\frac{1}{2}$ – ${\frac{2}{4}$ = 0 <=>
0,5 – 0,5 = 0 <=>
0 = 0
Der Punkt P3 (2|1) gehört zu der Funktion, da die Gleichung eine wahre Aussage ergibt.
P4 (4|2)
${\frac{2}{2}$ – ${\frac{4}{4}$ = 0 <=>
1 – 1 = 0 <=>
0 = 0
Die Aussage ist wahr und demzufolge gehört der Punkt P4 (4|2) zu der Funktion.
P5 (–8|10)
${\frac{10}{2}$ – ${\frac{–8}{4}$ = 0 <=>
5 + 2 = 0 <=>
7 = 0
Der Punkt P5 (–8|10) liegt nicht auf der Funktion, da die Aussage ein unwahres Ergebnis ergibt.
P6 (–2|–1)
${\frac{-1}{2}$ – ${\frac{-2}{4}$ = 0 <=>
–0,5 + 0,5 = 0 <=>
0 = 0
Der Punkt P6 (–2|–1) liegt auf der Funktion, da die Punktprobe eine wahre Aussage ergibt.
2. Mathematik-Nachhilfe-Aufgabe: Bestimme bei der linearen Funktion die Steigung, den Schnittpunkt mit der y-Achse und der x-Achse.
a) 4x + 5y = 5
Um die Steigung eindeutig bestimmen zu können, muss man die Funktion nach y hin umwandeln.
4x + 5y = 5 | – 4x <=>
5y = –4x + 5 | : 5 <=>
y = –${\frac{4}{5}$x + 1
Die Steigung der linearen Funktion ist –${\frac{4}{5}$. Den Schnittpunkt mit der y-Achse kann man nun auch sofort ablesen, diese ist Py (0|1). Um den Schnittpunkt mit der x-Achse zu bestimmen, muss man die nach y hin aufgelöste Funktionsgleichung gleich null setzen und anschließend nach x hin auflösen.
0 = –${\frac{4}{5}$x + 1 | + ${\frac{4}{5}$x <=>
${\frac{4}{5}$x = 1 | : ${\frac{4}{5}$x <=>
x = 1,25
Der Schnittpunkt mit der x-Achse liegt bei Px (1,25|0).
b) –3y + x = 0 | + 3y <=>
x = 3y | : 3 <=>
${\frac{1}{3}$x = y <=>
y = ${\frac{1}{3}$x
Die Steigung ist hier ${\frac{1}{3}$. Da bei dieser linearen Funktion kein n-Wert vorhanden ist, ist dieser null. Daher ist der Schnittpunkt mit der y-Achse Py (0|0).
0 = ${\frac{1}{3}$x | : ${\frac{1}{3}$ <=>
0 = x
Der Schnittpunkt mit der x-Achse ist bei dieser linearen Funktion Px (0|0).
c) 3y = 12x + 15 | : y <=>
y = 4x + 5
Die Steigung der linearen Funktion beträgt hier 4 und der Schnittpunkt mit der y-Achse ist hier Py (0|5).
0 = 4x + 5 | – 5 <=>
–5 = 4x | : 4 <=>
–${\frac{5}{4}$ = x <=>
x = –${\frac{5}{4}$
Die lineare Funktion weist den Schnittpunkt Px (–${\frac{5}{4}$|0) mit der x-Achse auf.
d) ${\frac{y}{4}$ + ${\frac{x}{2}$ – ${\frac{3}{4}$ = 0 | – ${\frac{x}{2}$ <=>
${\frac{y}{4}$ – ${\frac{3}{4}$ = – ${\frac{x}{2}$ | + ${\frac{3}{4}$ <=>
${\frac{y}{4}$ = – ${\frac{x}{2}$ + ${\frac{3}{4}$ | · 4 <=>
y = 2x + 3
Die lineare Funktion besitzt die Steigung 2 und den Schnittpunkt Py (0|3) mit der y-Achse.
0 = 2x + 3 | – 3 <=>
–3´= 2x | : 2 <=>
–${\frac{3}{2}$ = x <=>
x = –${\frac{3}{2}$
Der Schnittpunkt der der x-Achse ist hier Px (–${\frac{3}{2}$|0).
3. Mathe-Nachhilfe-Aufgabe: Bestimme die fehlenden Punkte so, dass diese zu den linearen Funktionen gehören: P1 (_|0), P2 (0|_), P3 (_|6), P4 (1|_), P5 (_|–0,6), P6 (–0,2|_).
Man setzt hier den gegebenen Wert des Punktes in die lineare Gleichung ein. Danach löst man die Gleichung nach der noch übrig gebliebenen Variablen auf. Dadurch erhält man dann den zweiten Wert des Punktes.
a) 2x – 5y = 0 <=>
P1 (_|0)
2x – 5 · (0) = 0 <=>
2x = 0 | : 2 <=>
x = 0
P1 (0|0)
a) 2x – 5y = 0 <=>
P2 (0|_)
2 · (0) – 5y = 0 <=>
0 – 5y = 0 | : (–5) <=>
y = 0
P2 (0|0)
a) 2x – 5y = 0 <=>
P3 (_|6)
2x – 5 · (6) = 0 <=>
2x – 30 = 0 | + 30 <=>
2x = 30 | : 2 <=>
x = 15
P3 (15|6)
a) 2x – 5y = 0 <=>
P4 (1|_)
2 · (1) – 5y = 0 <=>
2 – 5y = 0 | + 5y <=>
2 = 5y | : 5 <=>
${\frac{2}{5}$ = y <=>
y = ${\frac{2}{5}$
P4 (1|${\frac{2}{5}$)
a) 2x – 5y = 0 <=>
P5 (_|–0,6)
2x – 5 · (–0,6) = 0 <=>
2x + 3 = 0 | – 3 <=>
2x = –3 | : 2 <=>
x = –${\frac{3}{2}$
P5 (–${\frac{3}{2}$|–0,6)
a) 2x – 5y = 0 <=>
P6 (–0,2|_)
2 · (–0,2) – 5y = 0 <=>
–0,4 – 5y = 0 | + 5y <=>
–0,4 = 5y | : 5 <=>
–0,08 = y <=>
y = –0,08
P6 (–0,2|–0,08)
b) y + x = 1 <=>
P1 (_|0)
0 + x = 1 <=>
x = 1
P1 (1|0)
b) y + x = 1 <=>
P2 (0|_)
y + 0 = 1 <=>
y = 1
P2 (0|1)
b) y + x = 1 <=>
P3 (_|6)
6 + x = 1 | – 6 <=>
x = –5
P3 (–5|6)
b) y + x = 1 <=>
P4 (1|_)
y + 1 = 1 | – 1 <=>
y = 2
P4 (1|2)
b) y + x = 1 <=>
P5 (_|–0,6)
–0,6 + x = 1 | + 0,6 <=>
x = 1,6 <=>
P5 (1,6|–0,6)
b) y + x = 1 <=>
P6 (–0,2|_)
y – 0,2 = 1 | + 0,2 <=>
y = 1,2
P6 (–0,2|1,2)
c) 0,4y – 1,2x = 4,8 <=>
P1 (_|0)
0,4 · (0) – 1,2x = 4,8 <=>
–1,2x = 4,8 | : (–1,2) <=>
y = –4
P1 (–4|0)
c) 0,4y – 1,2x = 4,8 <=>
P2 (0|_)
0,4y – 1,2 · (0) = 4,8 <=>
0,4y = 4,8 | : 0,4 <=>
y = 12
P2 (0|12)
c) 0,4y – 1,2x = 4,8 <=>
P3 (_|6)
0,4 · (6) – 1,2x = 4,8 <=>
2,4 – 1,2x = 4,8 | – 2,4 <=>
–1,2x = 2,4 | : (–1,4) <=>
x = –2
P3 (–2|6)
c) 0,4y – 1,2x = 4,8 <=>
P4 (1|_)
0,4y – 1,2 · (1) = 4,8 <=>
0,4y – 1,2 = 4,8 | + 1,2 <=>
0,4y = 6 | : 0,4 <=>
y = 15
P4 (1|15)
c) 0,4y – 1,2x = 4,8 <=>
P5 (_|–0,6)
0,4 · (–0,6) – 1,2x = 4,8 <=>
–0,24 – 1,2x = 4,8 | + 0,24 <=>
– 1,2x = 5,04 | : (–1,2) <=>
x = –4,2
P5 (–4,2|–0,6)
c) 0,4y – 1,2x = 4,8 <=>
P6 (–0,2|_)
0,4y – 1,2 · (–0,2) = 4,8 <=>
0,4y + 0,24 = 4,8 | – 0,24 <=>
0,4y = 4,56 | : 0,4 <=>
y = 11,4
P6 (–0,2|11,4)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P1 (_|0)
${\frac{0}{3}$ + ${\frac{x}{2}$ = 2 <=>
${\frac{x}{2}$ = 2 | · 2 <=>
x = 4
P1 (4|0)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P2 (0|_)
${\frac{y}{3}$ + ${\frac{0}{2}$ = 2 <=>
${\frac{y}{3}$ = 2 | · 3 <=>
y = 6
P2 (0|6)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P3 (_|6)
${\frac{6}{3}$ + ${\frac{x}{2}$ = 2 <=>
2 + ${\frac{x}{2}$ = 2 | – 2 <=>
${\frac{x}{2}$ = 0 | · 2 <=>
x = 0
P3 (0|6)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P4 (1|_)
${\frac{y}{3}$ + ${\frac{1}{2}$ = 2 <=>
${\frac{y}{3}$ + 0,5 = 2 | – 0,5 <=>
${\frac{y}{3}$ = 1,5 | · 3 <=>
y = 4,5
P4 (1|4,5)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P5 (_|–0,6)
${\frac{-0,6}{3}$ + ${\frac{x}{2}$ = 2 <=>
–0,2 + ${\frac{x}{2}$ = 2 | + 0,2 <=>
${\frac{x}{2}$ = 2,2 | · 2 <=>
x = 4,4
P5 (4,4|–0,6)
d) ${\frac{y}{3}$ + ${\frac{x}{2}$ = 2 <=>
P6 (–0,2|_)
${\frac{y}{3}$ + ${\frac{-0,2}{2}$ = 2 <=>
${\frac{y}{3}$ – 0,1 = 2 | + 0,1 <=>
${\frac{y}{3}$ = 2,1 | · 3 <=>
y = 6,3
P6 (–0,2|6,3)
4. Mathe-Nachhilfe-Aufgabe: Es ist eine Gleichung mit zwei Variablen gegeben. Löse die Gleichung nach y hin auf und zeichne daraufhin die Funktion.
a)
3x – 5y = 20 | + 5y <=>
3x = 5y + 20 | – 20 <=>
3x – 20 = 5y | : 5 <=>
${\frac{3}{5}$x – 4 = y <=>
y = ${\frac{3}{5}$x – 4
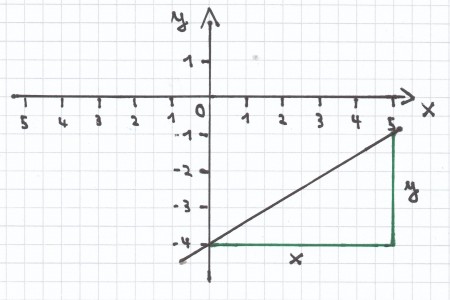
b)
2y + 4x = 20 | – 4x <=>
2y = –4x + 20 | : 2 <=>
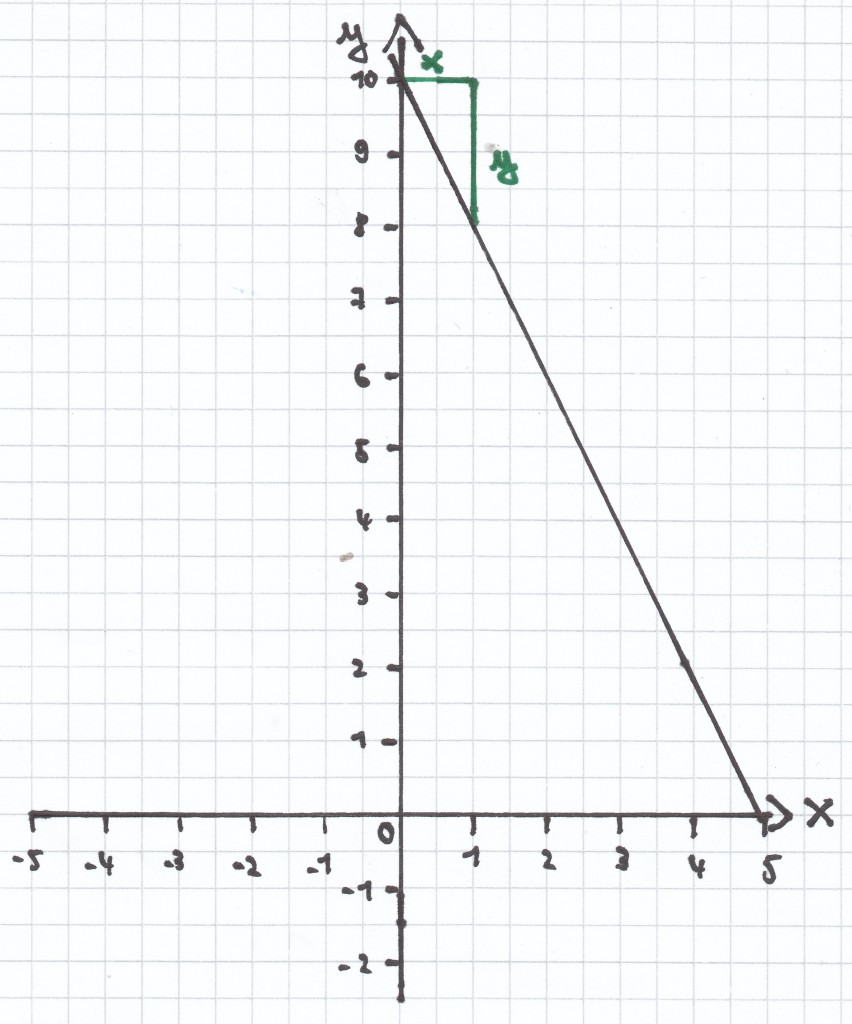
c)
y + ${\frac{x}{2}$ = –3,5 | – ${\frac{x}{2}$ <=>
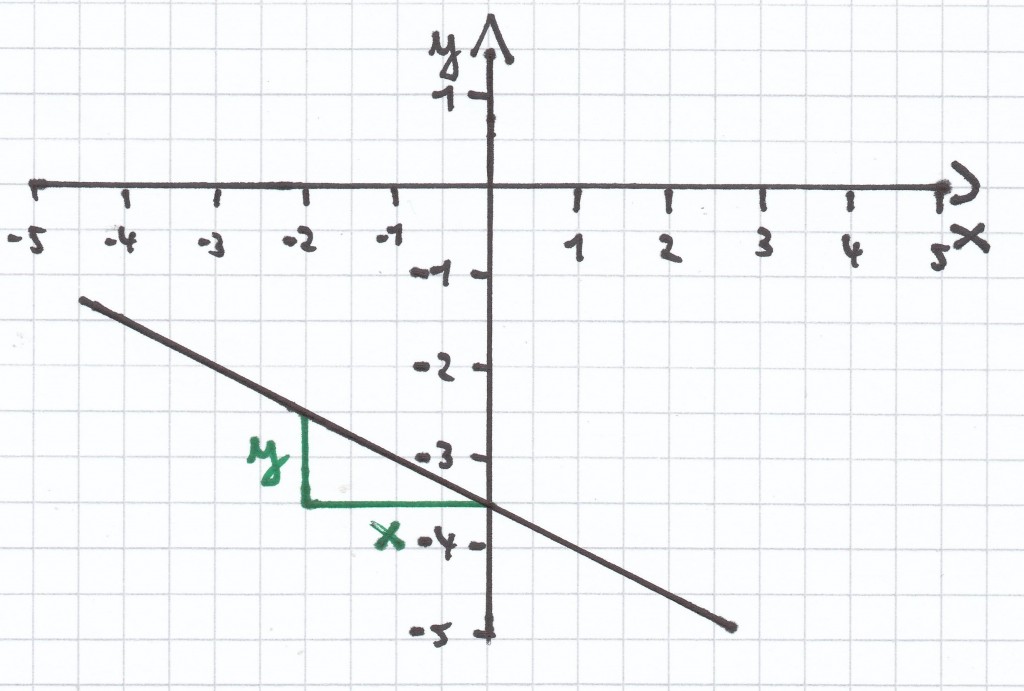
d)
${\frac{v~+~y}{4}$ = 1 | · 4 <=>
u + v = 4 | – u <=>