1. Grundlegendes zu Ungleichungen
In der Grundschule hat man normalerweise die Bedeutung und die richtige Handhabung des Zeichens „>“/„größer als“ und des Zeichens „<“/„kleiner als“ intensiv gelernt. Daher weiß man, wenn eine Zahl größer als die andere ist, dass man hierfür als Zeichen das „>“ verwendet. Bei den Zahlen 5 und 12 wird man daher sofort in der Sprache der Mathematik ausgedrückt schreiben können: 12 > 5. Ebenso weiß man sofort, wenn eine Zahl kleiner als eine andere Zahl ist, dass man dann das Zeichen „<“ hierfür verwendet. Bei den Zahlen 6 und 9 kann man deshalb sofort mathematisch wiedergeben: 6 < 9.
Das „>“/„größer als“ und das „<“/„kleiner als“ verwendet man daher in Mathe immer, wenn zwei Zahlen, die man miteinander vergleicht, nicht gleich sind. Wären die beiden Zahlen nämlich gleich, so würde man das hierfür in Mathematik gängige Zeichen benutzen, das „=“/„gleich“. Denn unstrittig wird jeder nicht auf den Kopf gefallene Mensch zustimmend nämlich Folgendes mathematisch wiedergeben, wenn man die Zahl 7 mit der Zahl 7 vergleicht: 7 = 7.
In der Mathematik kann man nun das „>“/„größer als“ und das „<“/„kleiner als“ genauso wie das „=“/„gleich“ nicht nur bei dem Vergleich von Zahlen verwenden, sondern auch im Zusammenhang mit Variablen und Termen. Verwendet man nun einen Term zusammen mit einem „>“/„größer als“ oder „<“/„kleiner als“, so liegt in der Mathematik eine sogenannte Ungleichung vor. Benutzt man hingegen das „=“/„gleich“, dann liegt hingegen eine Gleichung vor.
Beispiele für Ungleichungen mit einer Variablen, die jeweils die Potenz „hoch 1″ vorweisen:
- x + 2 > 5
- 3x > 2
- 8x + 3 < 12
- 7x – 21 > 12x + 9
- –23x – 9 < 18x – 11
2. Die Bestimmung der Lösungsmenge einer reinen Ungleichung
2.1 Ein bestimmter Zahlenbereich als Lösungsmenge
Die Lösungsmenge einer Ungleichung ermittelt man genauso wie bei einer Gleichung fast ausschließlich über Äquivalenzumformungen.
x + 2 > 5 | – 2 <=>
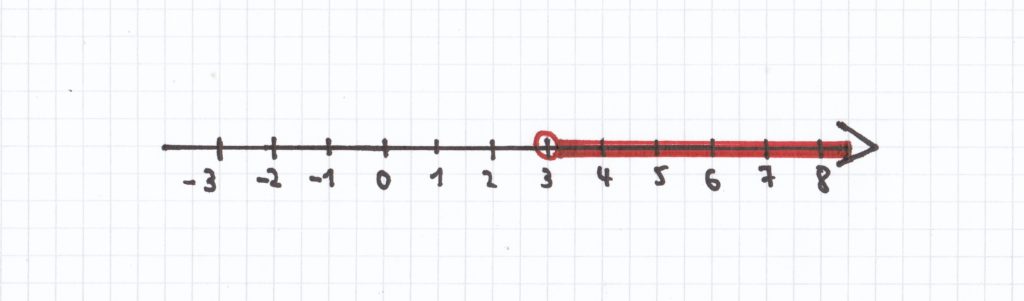
x > 3
L = {x | x > 3}
Die Lösungsmenge hier würde in Worten lauten: die Menge aller x, für die gilt, dass jedes x größer 3 eine Lösung der Ungleichung ist.
Im Vergleich zu Gleichungen unterscheidet sich aber bei Ungleichungen deren Lösungsmenge. Denn im Gegensatz zu Gleichungen liegt hier oft ein Zahlenbereich als Lösung vor.
2.2 Keine Lösung bei einer Ungleichung
Eliminiert sich das x innerhalb der Ungleichung, so kann die Lösungsmenge genau wie bei einer Gleichung entweder die leere Menge/{ } bzw. Ø sein oder die Menge aller Zahlen/ℚ oder ℝ.
x + 7 < x | – x <=>
7 < 0
L = { } bzw. Ø
Wie das Ergebnis nach der Elimination der Variablen x zeigt, bleibt die widersprüchliche Aussage stehen, dass 7 kleiner 0 ist. Daher gibt es hier für die Ungleichung keine Lösung.
2.3 Unendlich viele Lösungen bei einer Ungleichung
x + 4 > x | – x <=>
4 > 0
L = ℚ oder ℝ (je nach Klassenstufe)
Nach der Elimination der Variable ergibt sich hier als Ergebnis die Aussage, dass 4 größer 0 ist. Diese Aussage ist immer wahr. Daher gibt es für die Ungleichung hier unendlich viele Lösungen.
2.4 Ein bestimmter Zahlenbereich als Lösungsmenge bei einer Ungleichung der Form „≥“/„≤“
Neben dem bei einer Ungleichung normalerweise verwendeten Zeichen „>“/„größer als“ und „<“/„kleiner als“ können auch noch diese Zeichen vorkommen: „≥“/„größer gleich“ und „≤“/„kleiner gleich“. Besteht nun eine Ungleichung aus einem „≥“ oder „≤“, so sieht deren Lösungsmenge in der Regel geringfügig anders aus, als dies bei einer reinen Ungleichung der Fall wäre. Denn ein kleiner Unterschied kommt hier hinzu, wenn ein bestimmter Zahlenbereich als Lösungsmenge vorliegt.
x + 7 ≥ 14 | – 7 <=>
x ≥ 7
L = {x | x ≥ 7}
Die Lösungsmenge lautet hier in Worten ausgedrückt: die Menge alle x, für die gilt, dass jedes x größer 7 und x gleich 7 eine Lösung der Ungleichung ist.
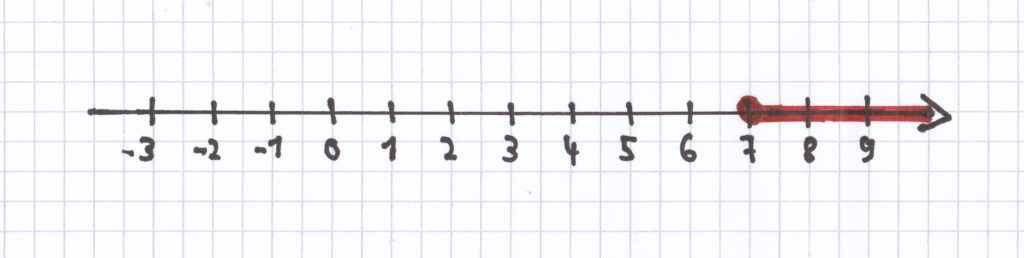
2.5 Keine Lösung bei einer Ungleichung der Form „≥“/„≤“
Keine Lösung liegt bei einer Ungleichung mit der Form „≥“/„≤“ genauso vor wie bei einer reinen Ungleichung, und zwar, wenn sich die Variable eliminiert, das Ergebnis aber widersprüchlich ist.
x + 2 ≤ x | – x <=>
2 ≤ 0
L = { } bzw. Ø
Da 2 niemals „kleiner gleich“ 0 ist, gibt es für die Ungleichung hier keine Lösung.
2.6 Unendlich viele Lösungen bei einer Ungleichung der Form „≥“/„≤“
Ungleichungen der Form „≥“/„≤“ liefern wie reine Ungleichungen genauso immer dann unendlich viele Lösungen, wenn sich zum einen die Variable eliminiert und zum anderen eine wahre Aussage entsteht.
x + 9 ≥ x | – x <=>
9 ≥ 0
L = ℚ oder ℝ (je nach Klassenstufe)
Da 9 „größer gleich“ 0 immer eine wahre Aussage der Ungleichung ist, gibt es hier unendlich viele Lösungen.
3. Das Umdrehen des Ungleichheitszeichens bei Ungleichungen
Die Äquivalenzumformungen bei Ungleichungen weisen eine Besonderheit auf, die es stets zu beachten gilt, und zwar das Umdrehen des Ungleichungszeichen bei einer Multiplikation oder Division mit einer negativen Zahl.
1. Beispiel
5x + 5 > 11 – x | + x <=>
6x + 5 > 11 | – 5 <=>
6x > 6 | : 6 <=>
x > 1
L = {x | x > 1}
Führt man bei einer Ungleichung, egal ob eine reine oder nicht, Äquivalenzumformungen mittels einer Addition/„+“, Subtraktion/„– “ oder Multiplikation/„·„eine Division/„:“ mit einer positiven Zahl durch, so bleibt die ursprüngliche Stellung des Ungleichheitszeichens stets gleich.
2. Beispiel
4x + 3 > 9 + 5x | – 5x <=>
–x + 3 > 9 | – 3 <=>
–x > 6 | · (–1) <=>
x < –6
L = {x | x < –6}
Führt man bei einer Ungleichung eine Äquivalenzumformung durch, bei der eine Multiplikation mit einem negativen Vorzeichen vorkommt, so dreht sich die ursprüngliche Stellung des Ungleichungszeichens um.
3. Beispiel
–x > 6 | : (–1) <=>
x < –6
L = {x | x < –6}
Das Gleiche gilt bei einer Division mit einer negativen Zahl. Auch hier dreht sich die ursprüngliche Stellung des Ungleichungszeichens um.