
1. Allgemeines zur Geometrie
Muss man in Mathematik gehäuft entweder ein Lineal, Geodreieck, einen Bleistift, Radiergummi oder einen Zirkel benutzen, ist allseits das Stöhnen in der Klasse groß. Denn im Mathe-Unterricht ist mal wieder Geometrie dran, ein großes, sehr umfangreiches Teilgebiet der Mathematik – das aber kaum einer Schülerin oder einem Schüler Spaß macht. Der Grund hierfür ist: An Mathe Interessierte wollen einfach viel lieber rechnen. Alles, was mit Zeichnen zu tun hat, gehört für diese eher in den Kunstunterricht. Nichtsdestotrotz wird man nicht daran vorbeikommen in der Grundschule, der Mittelstufe und, falls man Abitur machen möchte, in der Oberstufe sich in Mathe mit Geometrie zu reiben. Je höher jedoch die Klassenstufe ist, in der man sich befindet, desto mehr steht aber bei der Geometrie nicht nur das Zeichnen und Messen im Vordergrund – sondern auch das Rechnen. Dann ist auch mit ziemlicher Sicherheit wieder die Freude an den in Mathe-Interessierten entschieden höher!
Ganz grob kann man sagen, dass in Mathe in der Geometrie vom Punkt, der kleinsten geometrischen Darstellungsform, über Strecken und Flächen bis hin zu unterschiedlichen Körpern, dreidimensionalen Darstellungsformen, alles auf einem Blatt zeichnerisch wiedergegeben werden muss. Anfangs steht hierbei mehr das Zeichnen und Messen im Vordergrund, später immer mehr das Zeichnen und Rechnen. Eine große Genauigkeit ist aber in Geometrie von Anfang an wichtig! Daher müssen alle Hilfsmittel, wie Lineal, Geodreieck und Lineal, ohne irgendwelche Einschränkungen verwendet werden können. Ein guter Radiergummi und ein gespitzter Bleistift gehört hier ebenso dazu. Nur so ist nämlich die Grundvoraussetzung gewährleistet, dass alle geometrischen Darstellungen weitestgehend den geforderten Vorgaben in Abhängigkeit zu der jeweiligen Aufgabenstellungen entsprechen können. Bei in Anführungszeichen fehlerhaftem „geometrischen Handwerkszeug“ ist dies schließlich keineswegs gegeben, da dann die konkrete Umsetzung auf dem Papier oftmals nicht genau genug ist. Man kann das mit einem Handwerker vergleichen, der seine gelernte Tätigkeit nur gut ausüben kann, wenn sein hierfür notwendiges Equipment tadellos ist.
- Ein Punkt mit der Bezeichnung A sieht auf einem Blatt zeichnerisch dargestellt folgendermaßen aus:

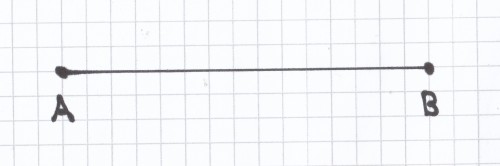
- Eine Strecke, die von den beiden Punkten A und B begrenzt wird, sieht zeichnerisch dargestellt wie folgt aus:
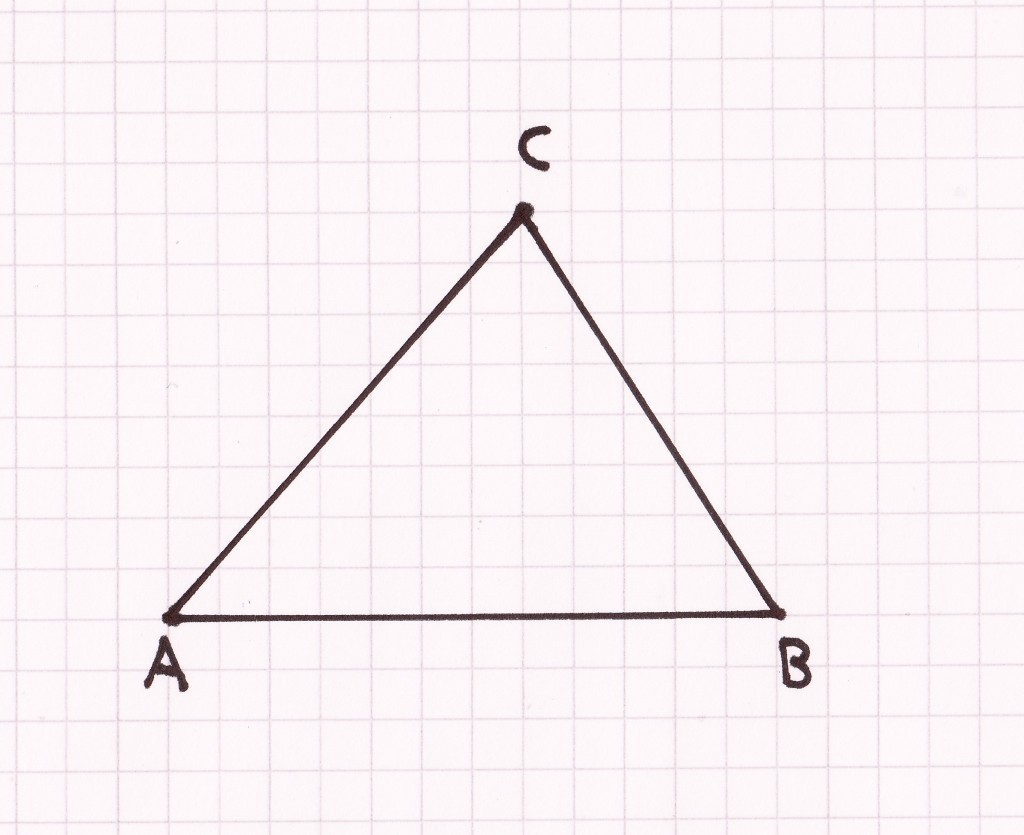
- Die kleinste Darstellung einer Fläche ist mittels drei Punkten möglich. Die hierbei entstehende geometrische Form ist ein Dreieck.
Auch kreisförmige Flächen kann man im Prinzip auf zwei gebogene Strecken zurückführen, die zusammen als zwei Kreisbögen einen Kreis bilden.
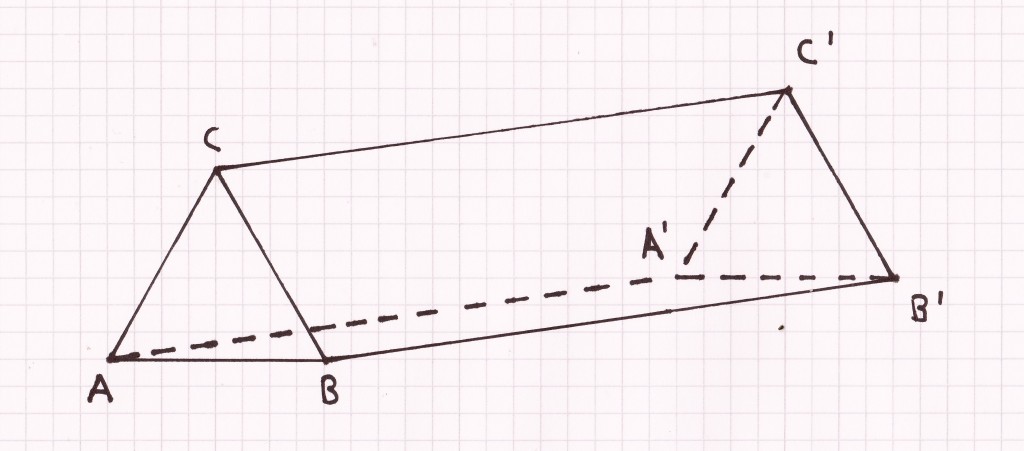
- Ein einfacher Körper, dessen Grund- und Deckfläche ein Dreieck bilden, stellt ein dreiseitiges Prisma dar:
Es gibt auch Körper, die nicht ein x-beliebiges Vieleck als Grund- und Deckfläche haben, sondern einen Kreis. Diese werden Zylinder genannt, wenn, wie bei einem Prisma diese beiden Flächen parallel zueinander stehen und auch noch konkruent (deckungsgleich) sind.