1. Bestandteile und Besonderheiten einer Potenz
Potenzen sind Zahlen oder Buchstaben, die sowohl eine Basis als auch einen Exponenten vorweisen. Das lernt man bereits in der Grundschule in Mathe. Auch lernt man hierbei, wie eine Potenz entsteht, nämlich durch eine besondere Multiplikation, bei der die Faktoren jeweils gleich sind.
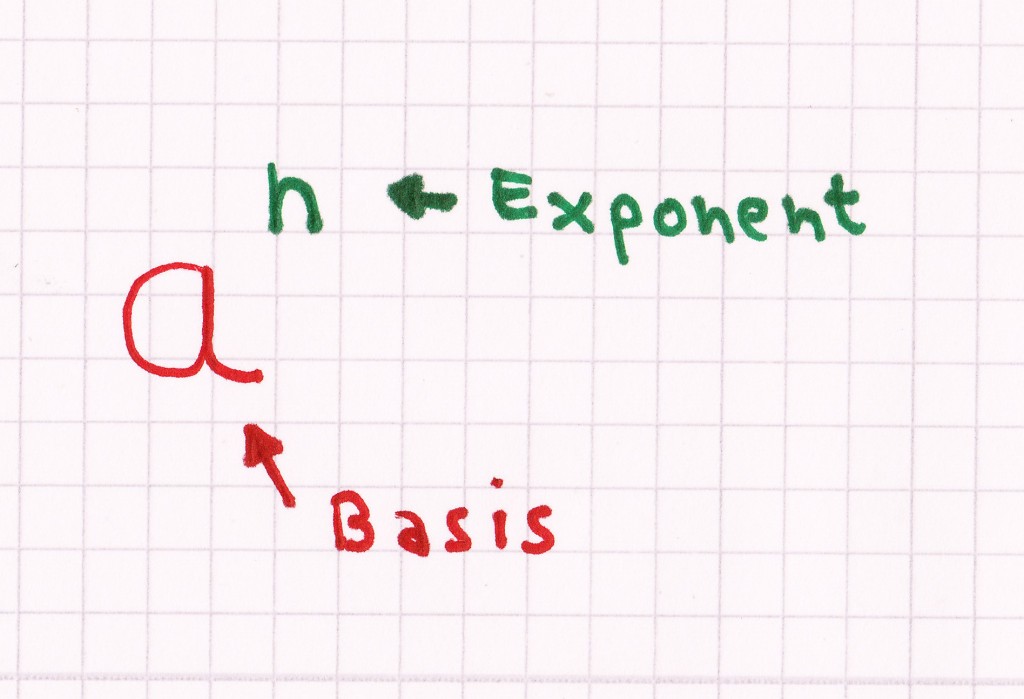
Aus dem gerade Gesagten ergibt sich demzufolge, dass:
38 = 3 · 3 · 3 · 3 · 3 · 3 · 3 · 3
oder:
(–6)5 = (–6) · (–6) · (–6) · (–6) · (–6)
oder:
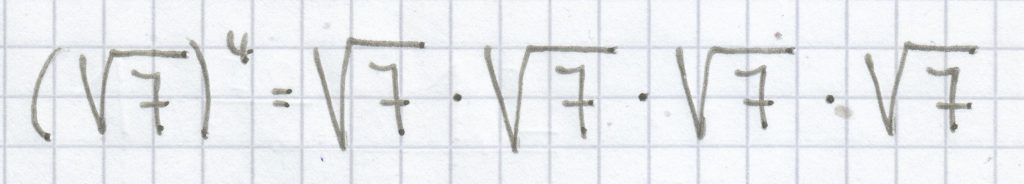
oder:
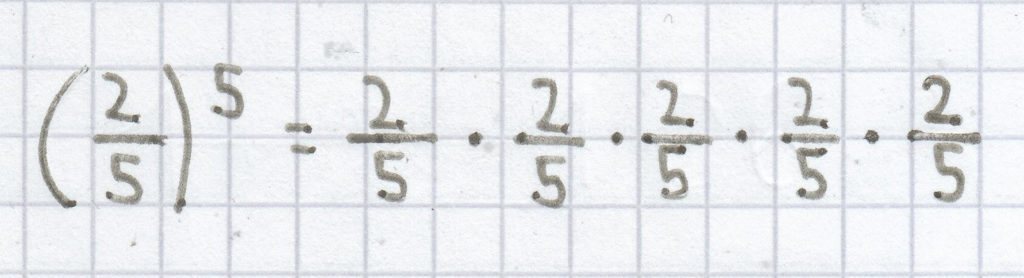
Allgemein kann man daher eine Potenz folgendermaßen definieren:
a1 = a
a2 = a · a
a3 = a · a · a
a4 = a · a · a · a
an = a · a · a … · a (n Faktoren von a), (für a є ℝ, n є ℕ*)
Bei einer Potenz gibt es zwei Besonderheiten, und zwar, wenn der Exponent eine Null vorweist oder wenn der Exponent negativ ist. Dann gilt folgende Definition:
a0 = 1
sowie
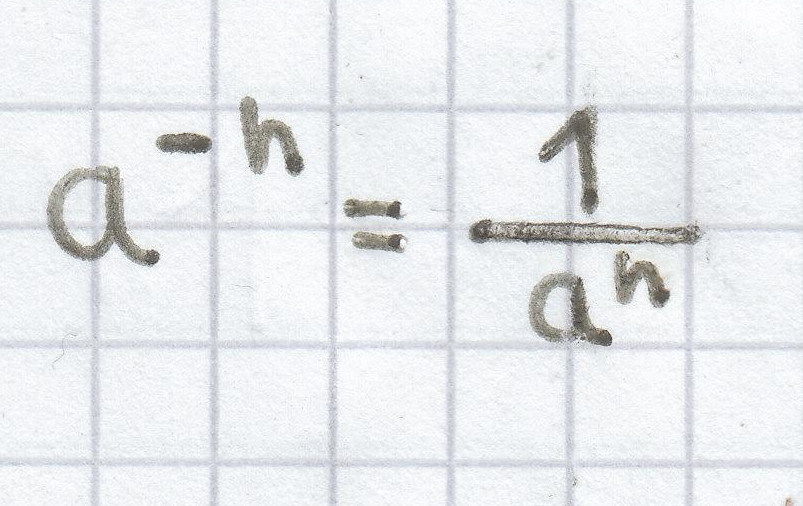
(für a ≠ 0, n є ℕ*)
Beispiele:
30 = 1
(–6)0 = 1
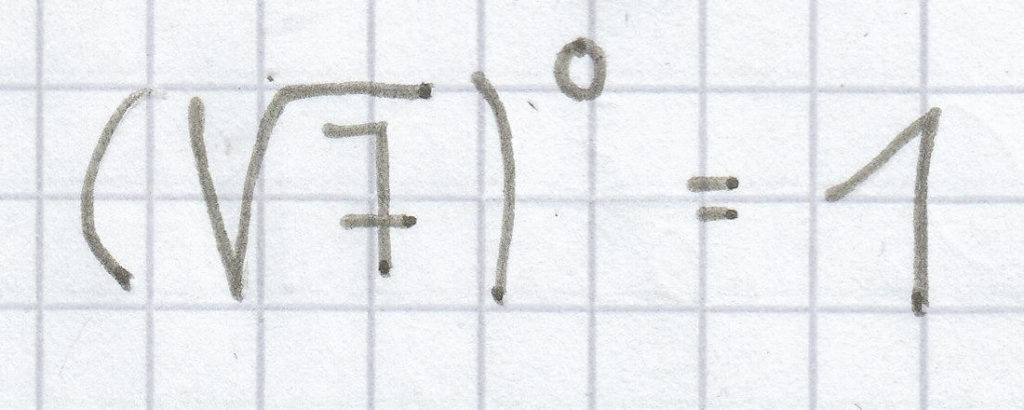
;
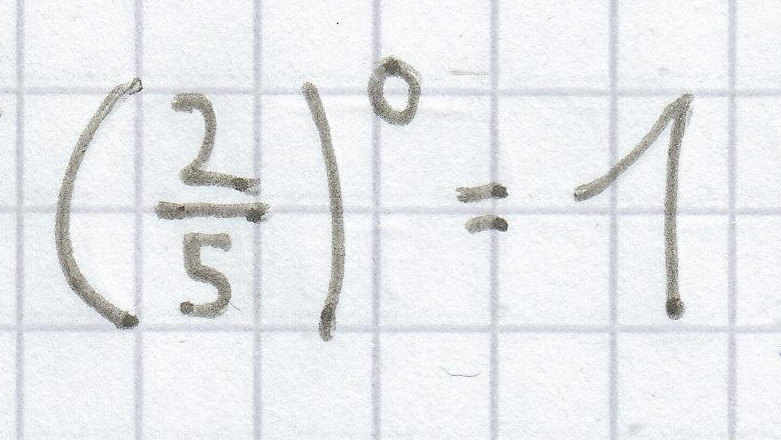
;
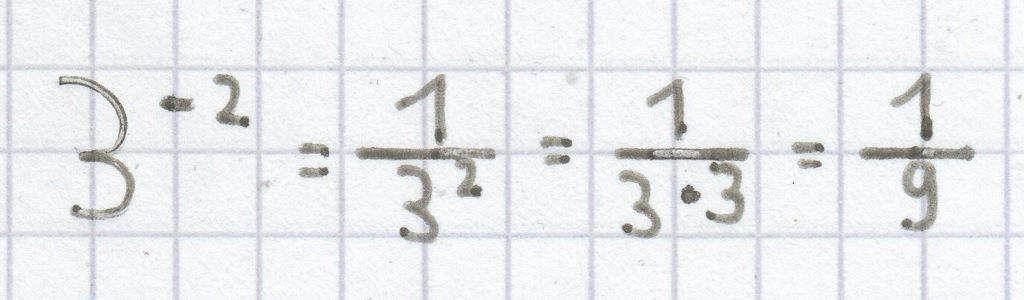
;

;
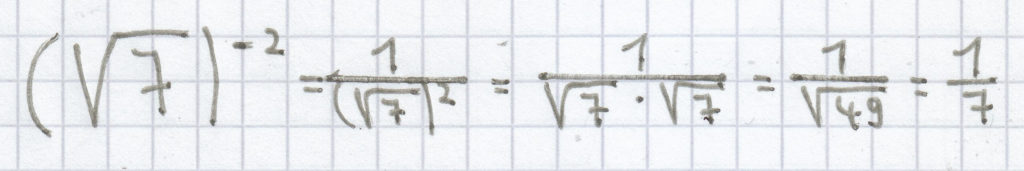
;
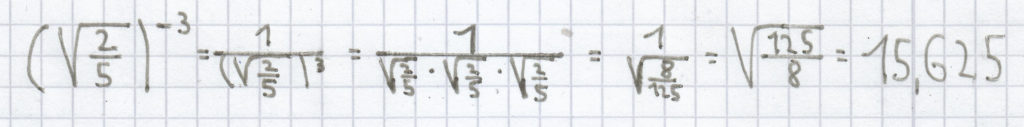
Eine Potenz mit der Basis 0 und einem negativen Exponenten ist nicht definiert.
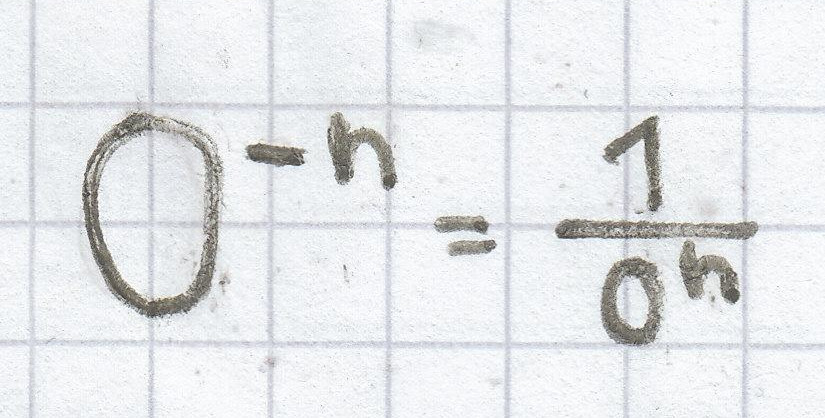
.
Wie man nach der Umformung sieht, steht im Nenner des Bruchs eine Null. Aus dem Mathe-Unterricht weiß man, dass solch ein Bruch nicht definiert ist.
2. Potenzgesetze
Wie alle Rechenoperationen, die man in der Schule in Mathematik gelernt hat, bestimmten Gesetzmäßigkeiten unterliegen, so ist dies auch bei Potenzen der Fall. Diese nennt man Potenzgesetze. Die Potenzgesetze werden folgendermaßen unterteilt:
- Potenzgesetz für die Multiplikation von Potenzen mit gleicher Basis
- Potenzgesetz für die Multiplikation von Potenzen mit gleichem Exponenten
- Potenzgesetz für das Potenzieren einer Potenz
- Potenzgesetz für die Division von Potenzen mit gleicher Basis
- Potenzgesetz für die Division von Potenzen mit gleichem Exponenten
2.1 Potenzgesetz für die Multiplikation von Potenzen mit gleicher Basis
Liegt eine Multiplikation von Potenzen mit gleicher Basis vor, so ergibt sich hierbei diese Gesetzmäßigkeit:
am · an = am + n (für a ≠ 0, m є Z, n є Z).
Die gleichen Basen werden miteinander multipliziert, indem man deren Exponenten addiert. Die Basis bleibt hierbei bestehen.
Beispiele:
52 · 57 = 5 2 + 7 = 59
3– 2 · 37 = 3– 2 + 7 = 35
2– 4 · 2– 5 = 2(–4) + (–5) = 2– 9 (–6)4 · (–6)3 = (–6)4 + 3 = (–6)7
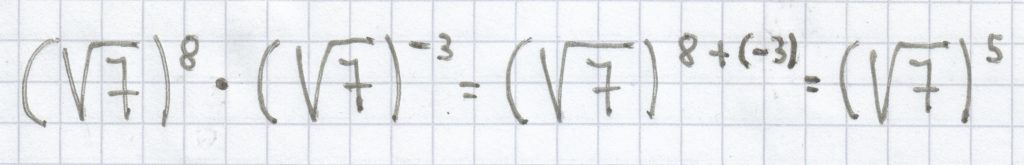
2.2 Potenzgesetz für die Multiplikation von Potenzen mit gleichem Exponenten
Liegt eine Multiplikation von Potenzen vor, deren Exponenten gleich sind, so ergibt sich diese Regelmäßigkeit:
an · bn = (a · b)n (für a ≠ 0, b ≠ 0, n є Z).
Die Basen werden miteinander multipliziert und der Exponent bleibt bestehen.
Beispiele:
87 · 57 = (8 · 5)7 = 407
45 · (–7)5 = (4 · (–7))5 = –285
(–3)2 · (–3)2 = ((–3) · (–3))2 = 92
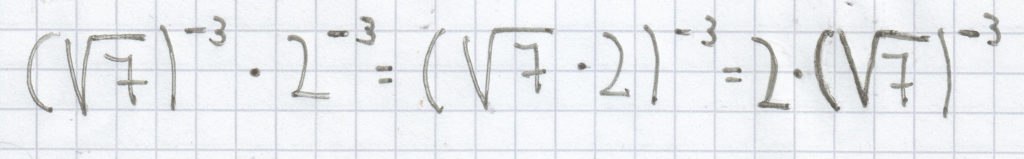
Beachte bei der Multiplikation der Basen auf die bei der Multiplikation geltenden Vorzeichenregeln.
2.3 Potenzgesetz für das Potenzieren einer Potenz
Potenziert man eine Potenz mit einer weiteren Potenz, so ergibt sich folgende Regelmäßigkeit:
(am)n = am · n (für a ≠ 0, m є Z, n є Z).
Eine Potenz wird potenziert, indem man die beiden Exponenten miteinander multipliziert. Die Basis bleibt hierbei bestehen.
Beispiele:
(53)2 = 53 · 2 = 56;
(2–4)5 = 2(–4) · 5 = 2 – 20;
(–83)–7= (–8)3 · (–7) = (–8)– 21
2.4 Potenzgesetz für die Division von Potenzen mit gleicher Basis
Liegt ein Bruch vor, bei dem Zähler und Nenner die gleiche Basis besitzen, dann gilt diese Regelmäßigkeit:
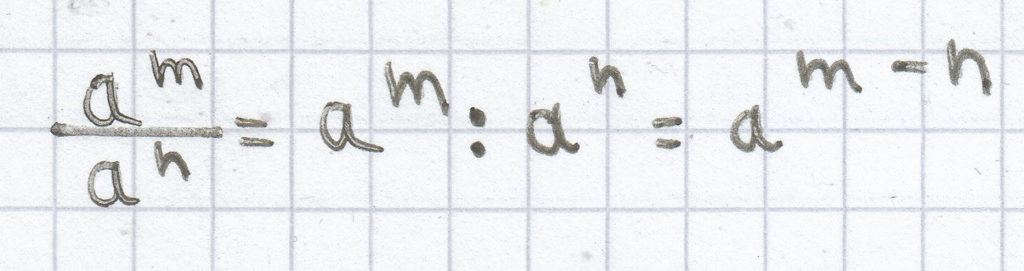
(für a ≠ 0, m є Z, n є Z).
Man zieht die Exponenten voneinander ab, wenn bei einem Bruch im Zähler und im Nenner die gleiche Basis auftritt. Die Basis bleibt bestehen.
Beispiele:
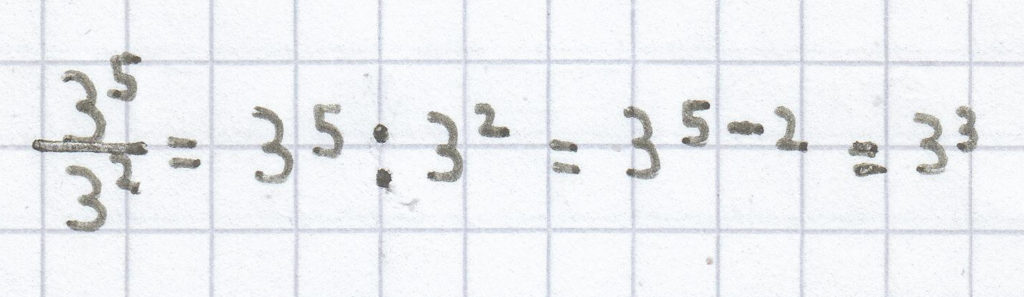
;
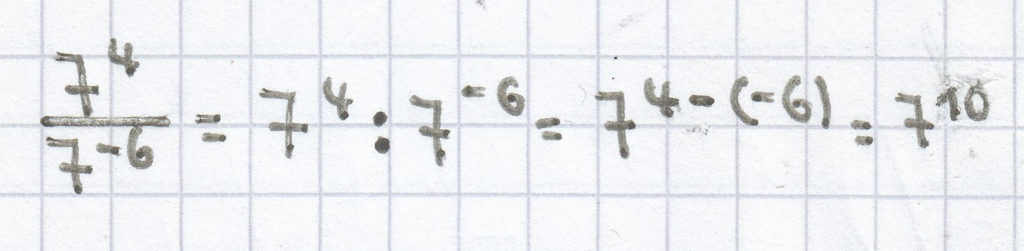
;

;
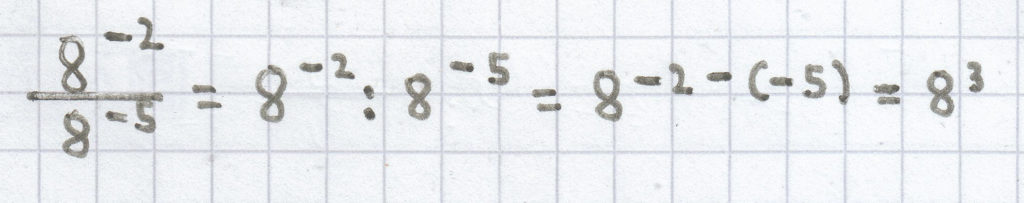
2.5 Potenzgesetz für die Division von Potenzen mit gleichen Exponenten
Weisen bei einem Bruch sowohl der Zähler als auch der Nenner den gleichen Exponenten auf, so gilt diese Gesetzmäßigkeit:
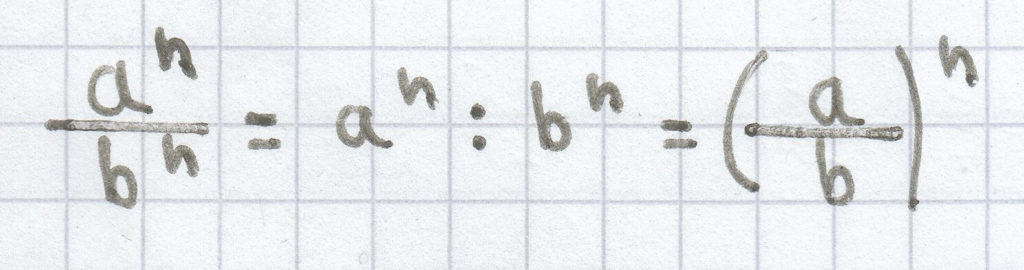
(für a ≠ 0, b ≠ 0 = n є Z).
Man dividiert die Basen, wenn bei einem Bruch die gleichen Exponenten im Zähler und Nenner auftreten. Der Exponent bleibt bestehen.
Beispiele:
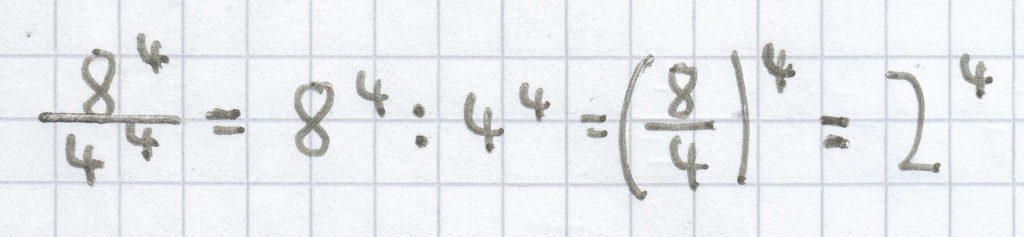
;
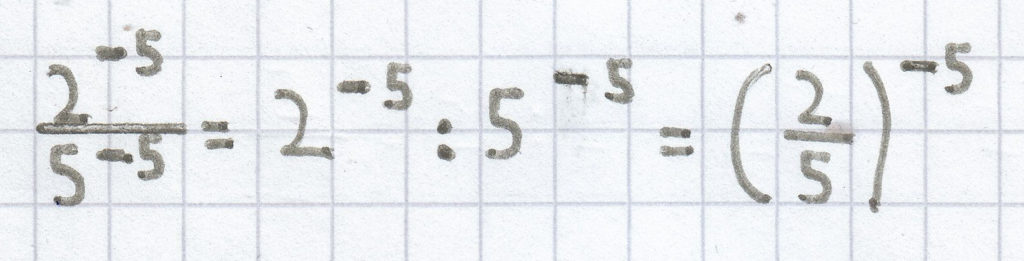
;
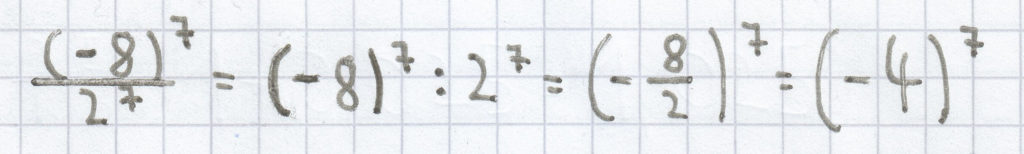
;
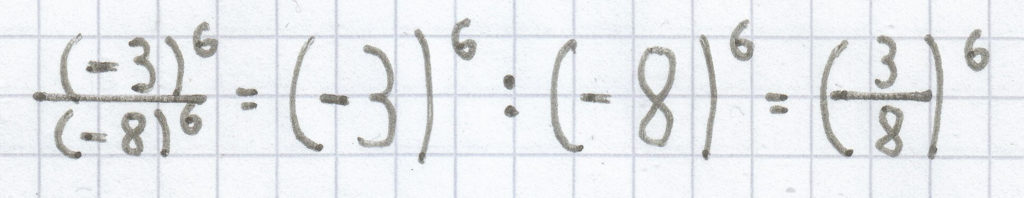
Achte auch auf die geltenden Vorzeichenregeln bei der Division.