Umfang

1. Allgemeines zum Umfang bei Vielecken

Ein Vieleck besteht aus Punkten, die eine Fläche bilden. Bei der Fläche eines Vielecks kann man nun nicht nur dessen Flächeninhalt bestimmen, sondern auch dessen Umfang. Der Umfang eines Vielecks ist hierbei immer die äußere Begrenzung der Fläche mittels der Seitenlängen. In der Schule in Mathe lernt man aber auch als Eselsbrücke, dass der gesamte Weg, den man bei einem Vieleck außen herum einmal gedanklich ablaufen kann, immer der Umfang darstellt.

Daher lässt sich der Umfang bei Vielecken auch wiedergebe als die Summe aller Seitenlinien.

2. Der Umfang bei Dreiecken

Ein Dreieck besteht bekanntlich aus drei Seitenlängen. Hierbei gibt es Dreiecke, die drei unterschiedliche Seitenlängen vorweisen. Das sind im Prinzip ganz normale Dreiecke. Darüber hinaus gibt es Dreiecke, bei denen zwei Seitenlinien gleich lang sind. Solch ein Dreieck wird als ein gleichschenkliges Dreieck bezeichnet. Des Weiteren gibt es Dreiecke, deren Seitenlängen alle gleich lang sind. Diese Dreiecke nennt man gleichseitige Dreiecke.

2.1 Der Umfang bei einem normalen Dreieck

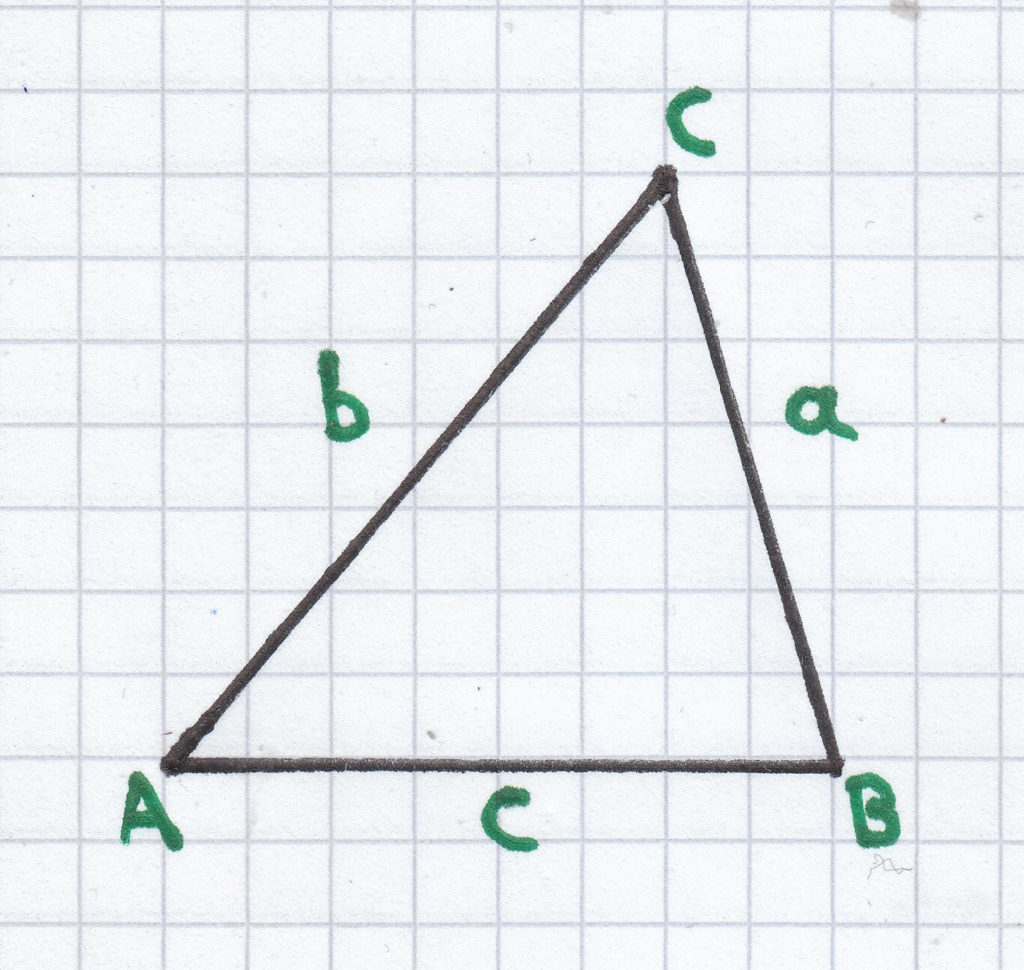
Der Umfang eines normalen Dreiecks berechnet man folgendermaßen:

U_D = a + b + c

Beispiel:

Ein Dreieck hat die Seitenlänge a = 10 cm, b = 8 cm und c = 5 cm. Der Umfang des Dreiecks beträgt dann:

U_D = 10 cm + 8 cm + 5 cm = 23 cm

2.2 Der Umfang bei einem gleichschenkligen Dreieck

Der Umfang eines gleichschenkligen Dreiecks kann man wie bei einem normalen Dreieck berechnen:

U_D = a + b + c

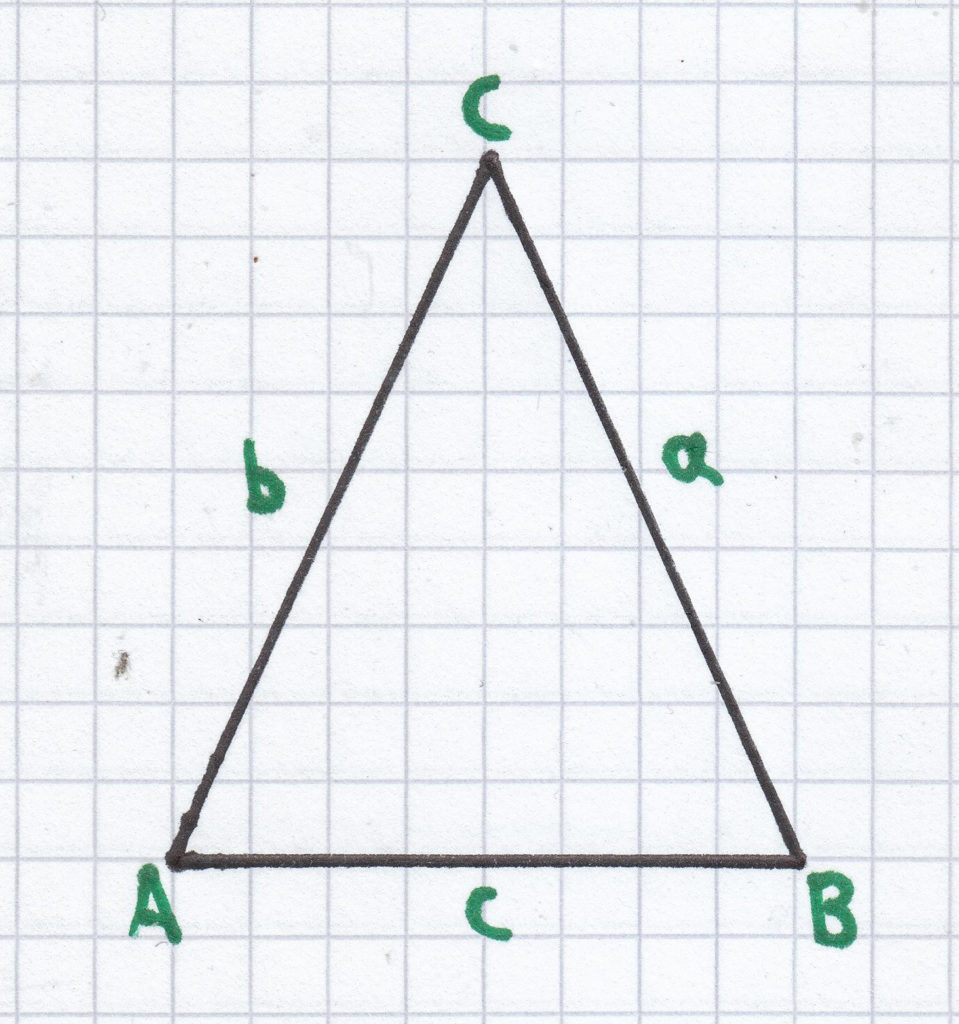
Da zwei Seitenlängen bei einem gleichschenkligen Dreieck immer gleich groß sind, ergeben sich folgende drei möglichen Berechnungen des Umfangs:

U_D = a + b + c; da gilt a = b, ergibt sich:

U_D = a + a + c = 2a + c

bzw.

U_D = b + b + c = 2b + c

U_D = a + b + c; da gilt: b = c, ergibt sich:

U_D = a + b + b = 2b + a

bzw.

U_D = a + c + c = 2c + a

U_D = a + b + c; da gilt a = c, ergibt sich:

U_D = a + a + b = 2a + b

bzw.

U_D = b + c + c = 2c + b

Beispiel:

Ein Dreieck hat die Seitenlängen a = 6,67 cm, b = 5 cm und c = 5 cm. Da zwei Seitenlängen hier gleich groß sind und es sich demzufolge um ein gleichschenkliges Dreieck handelt, beträgt der Umfang:

U_D = 6,67 cm + 2 · 5 cm = 16,67 cm.

2.3 Der Umfang bei einem gleichseitigen Dreieck

Genauso wie bei einem normalen Dreieck kann man auch bei einem gleichseitigen Dreieck den Umfang berechnen:

U_D = a + b + c

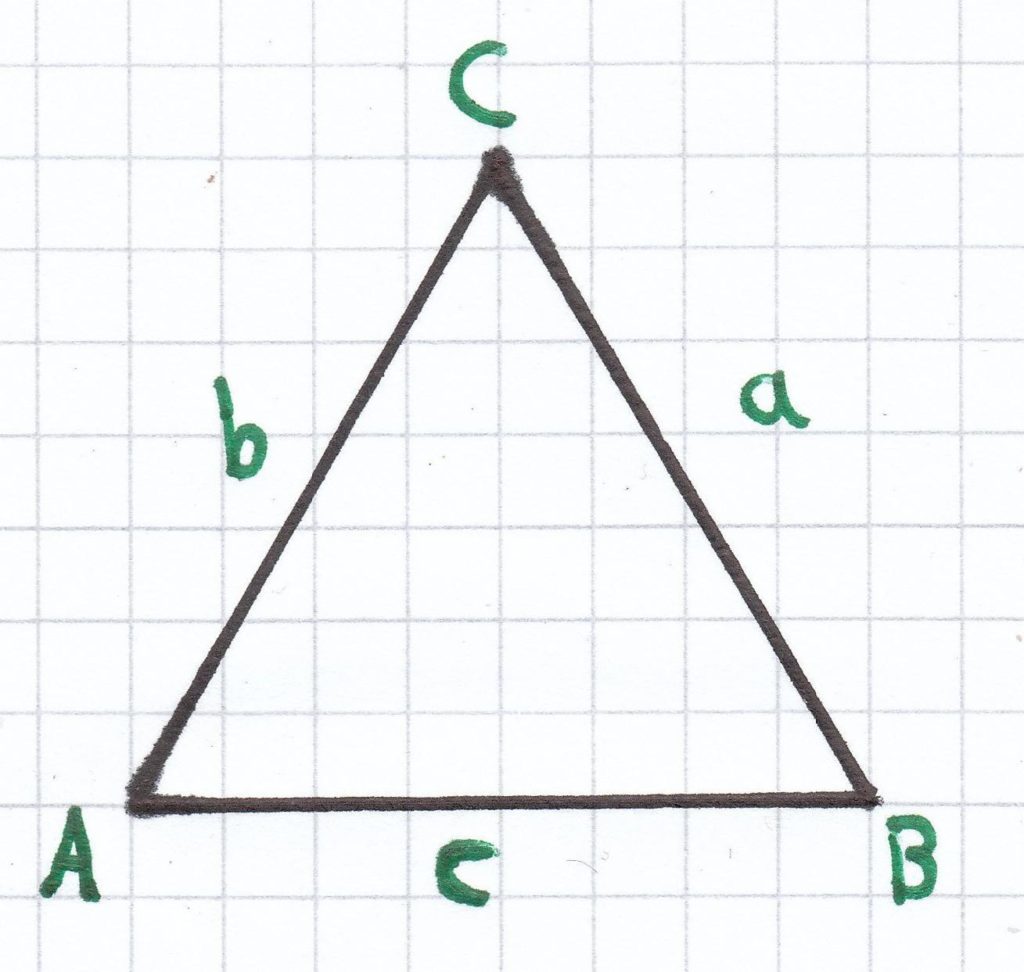
Da bei einem gleichseitigen Dreieck alle Seitenlängen gleichgroß sind, kann man auch den Umfang wie folgt berechnen:

U_D = a + b + c = 3a = 3b = 3c

Beispiel:

Bei einem gleichseitigen Dreieck ist die Seitenlänge 7 cm. Daraus ergibt sich, dass a = 7 cm, b = 7 cm und c = 7 cm ist. Der Umfang beträgt hier also:

U_D = 3 · 7 cm = 21 cm.

3. Der Umfang bei Vierecken

Ein Viereck weist bekanntlich vier Seiten auf. Besitzt ein Viereck unterschiedliche Seitenlängen, so handelt es sich hierbei um ein ganz normales Viereck. Hat ein Viereck zwei oder vier gleiche Seitenlängen, dann liegt ein besonderes Viereck vor.

3.1 Der Umfang bei einem normalen Viereck

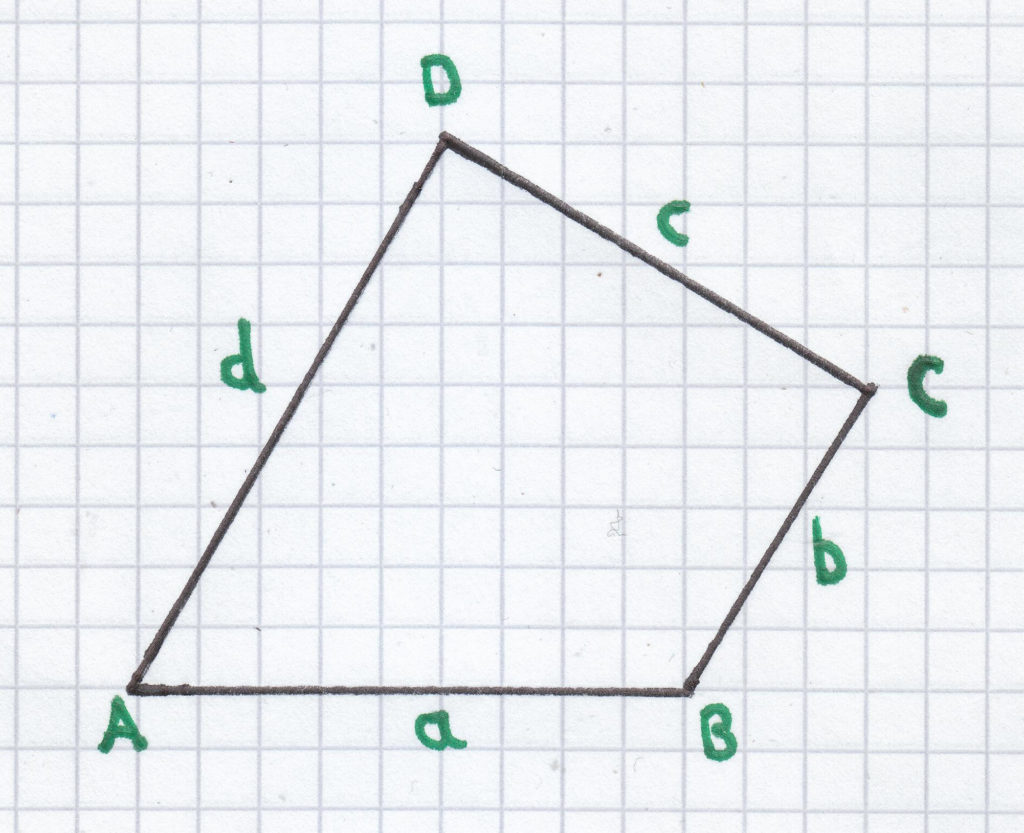
Der Umfang eines normalen Vierecks berechnet man wie folgt:

U_V = a + b + c + d

Beispiel:

Ein Viereck hat die Seitenlängen a = 4 cm, b = 5 cm, c = 3 cm und d = 5,2 cm. Der Umfang des Vierecks beträgt dann:

U_V = 4 cm + 5 cm + 3 cm + 5,2 cm = 17,2 cm.

3.2 Der Umfang bei einem Rechteck

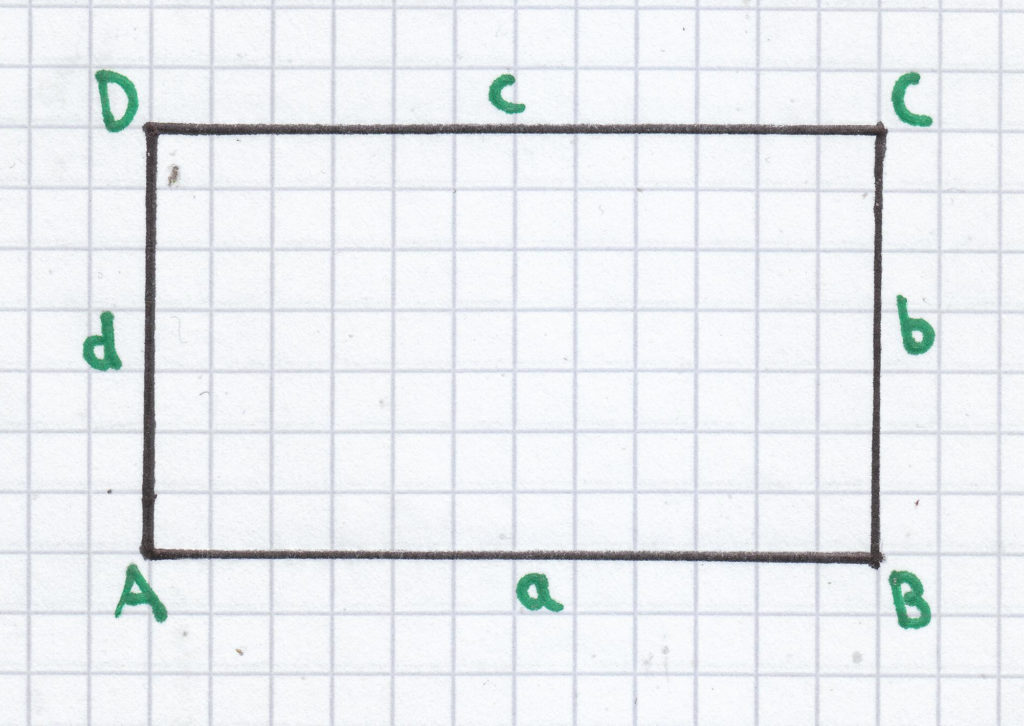
Der Umfang bei einem Rechteck berechnet man wie folgt:

U_R = a + b + c + d; da gilt: a = c und b = d ergibt sich:

U_R = a + a + b + b =

U_R = 2a + 2b

bzw.

U_R = c + c + d + d =

U_R = 2c + 2d

Beispiel:

Ein Rechteck hat die Länge = 5 cm und die Breite = 3 cm. Der Umfang des Rechtecks beträgt daher:

U_R = 2 · 5 cm + 2 · 3 cm = 16 cm.

3.3 Der Umfang bei einem Quadrat

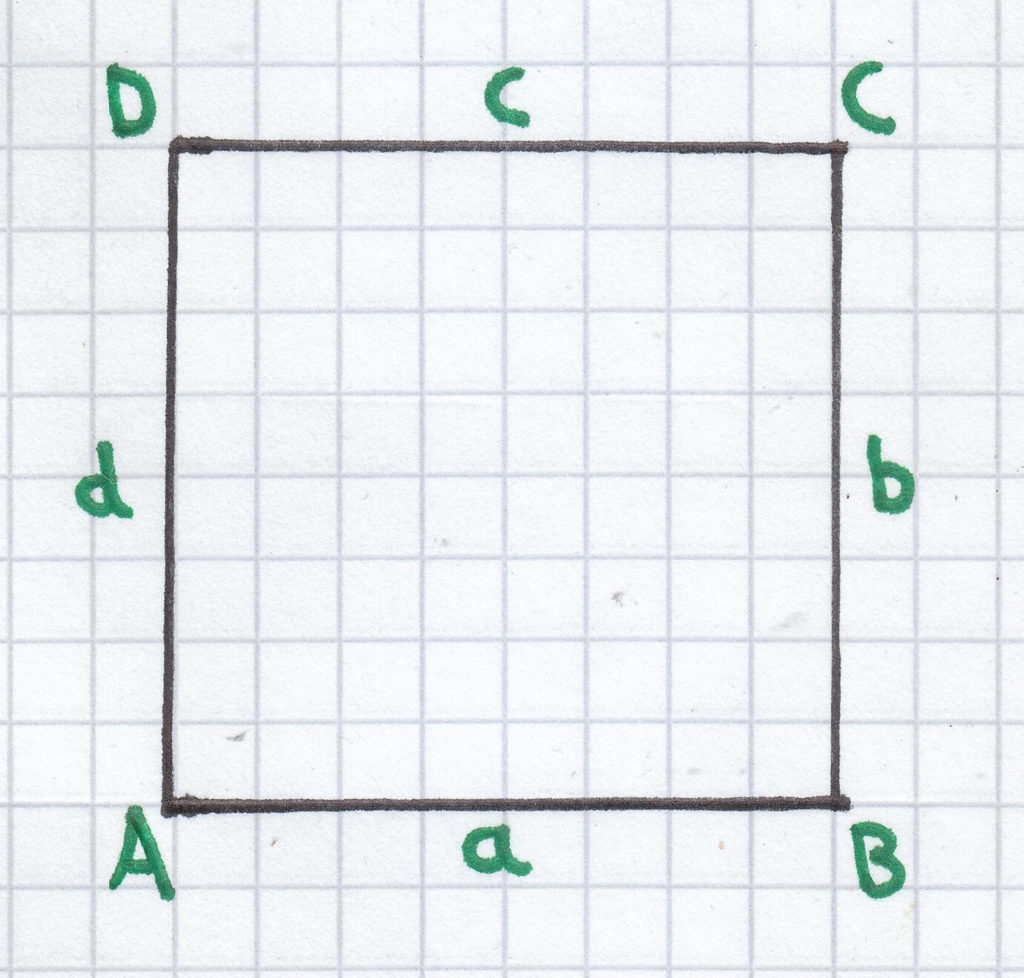
Der Umfang bei einem Quadrat rechnet man folgendermaßen:

U_Q = a + b + c + d; da gilt a = b = c = d ergibt sich:

U_Q = a + a + a + a = 4a

bzw.

U_Q = b + b + b + b = 4b

bzw.

U_Q = c + c + c + c = 4c

bzw.

U_Q = d + d + d + d = 4d

Beispiel: 

Ein Quadrat hat die Seitenlänge 7 cm. Der Umfang des Quadrats beträgt daher:

U_Q = 4 · 7 cm = 28 cm.

3.4 Der Umfang bei einem Parallelogramm

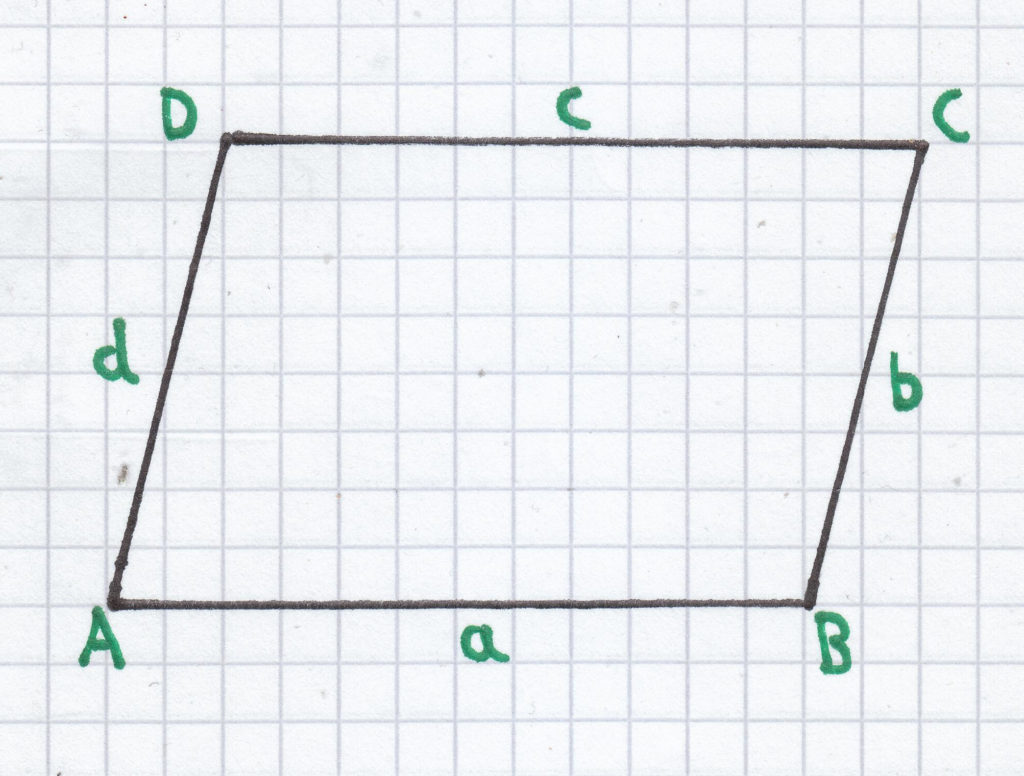
Der Umfang bei einem Parallelogramm beträgt:

U_P = a + b + c + d; da gilt a = c und b = d erigbt sich:

U_P = a + a + b + b = 2a + 2b

bzw.

U_P = c + c + d + d = 2c + 2d

Beispiel:

Ein Parallelogramm hat die Seitenlängen a = 6 und b = 5 cm. Der Umfang des Parallelogramms ist daher:

U_P = 2 · 6 cm + 2 · 5 cm = 22 cm.

3.5 Der Umfang bei einem Trapez

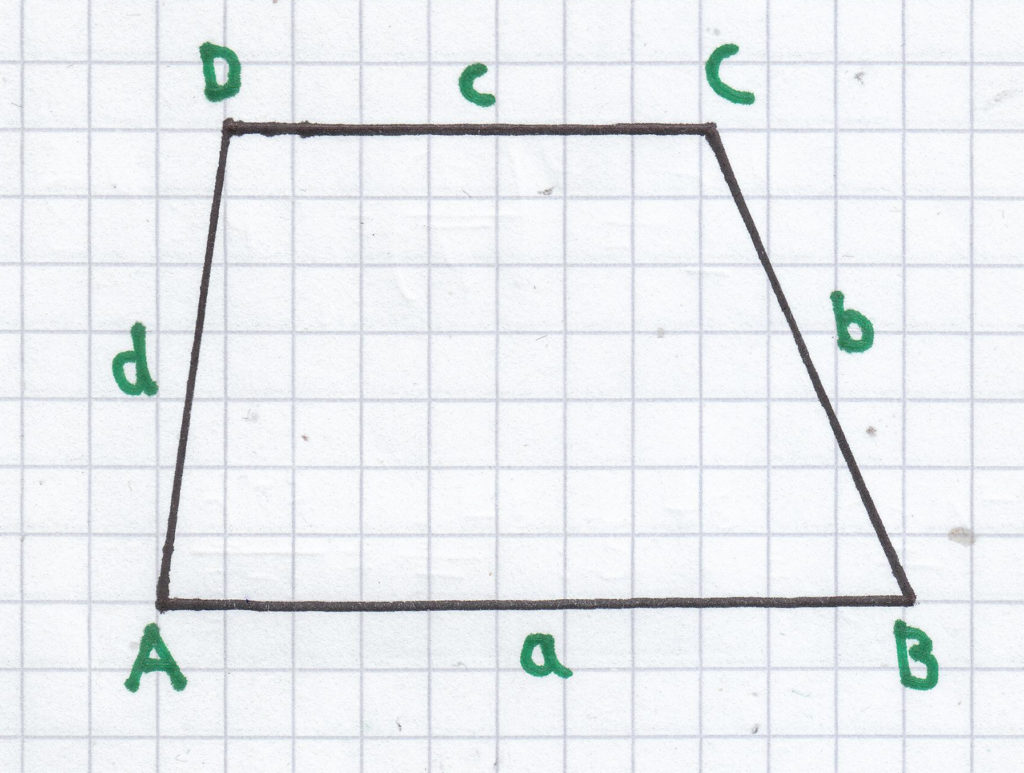
Der Umfang bei einem Trapez beträgt:

U_T = a + b + c + d

Beispiel:

Ein Trapez hat die Seitenlängen a = 8 cm, b = 5 cm, c = 4 cm und d = 4 cm. Der Umfang des Trapezes ist daher: 

U_T = 8 cm + 5 cm + 4 cm + 4 cm = 21 cm.

3.6 Der Umfang bei einem Drachenviereck

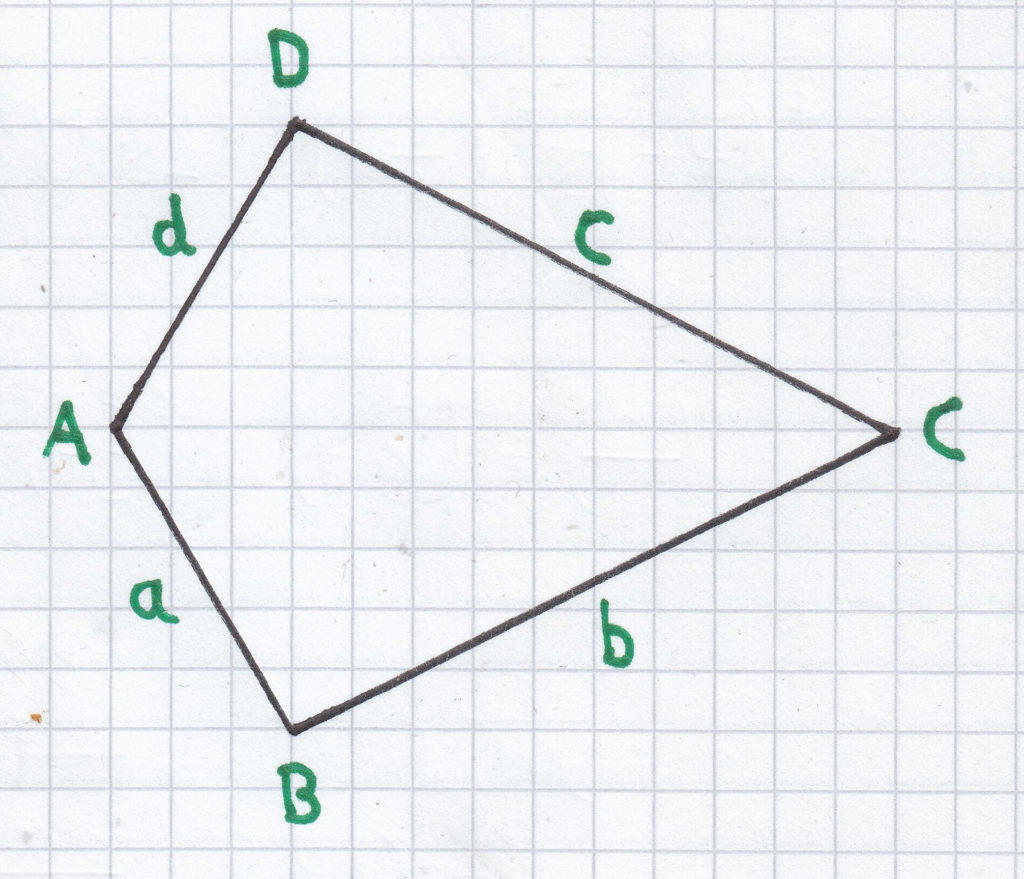
Der Umfang bei einem Drachenviereck berechnet sich folgendermaßen:

U_Dr = a + b + c + d; da gilt a = d und b = c, ergibt sich:

U_Dr = 2a + 2b

bzw.

U_Dr = 2c + 2d

bzw.

U_Dr = 2a + 2c

bzw.

U_Dr = 2b + 2d

Beispiel:

Ein Drachenviereck hat die Seitenlängen a = 3 cm und b = 7 cm. Der Umfang des Drachenvierecks ist daher:

U_Dr = 2 · 3 cm + 2 · 7 cm = 20 cm.