
Bei der von Mathematik-Lehrern an Schüler gerichteten Frage: „Term oder Therme – auf was habt ihr heute mehr Lust?“ würden sich ohne Frage die meisten Schulbankdrücker ganz klar für die Badeanstalt entscheiden. Im Wasser planschen, mit anderen um die Wette schwimmen oder einfach nur im Entspannungsbad „abhängen“ macht natürlich viel mehr Spaß, als im Mathe-Unterricht zu sitzen – und sich mit Termen „herumzuschlagen“. Phonetisch beziehungsweise lautlich liegen beide Begriffe Term und Therme zwar äußerst nahe beieinander – wie die Schüler-Reaktionen auf die oben gestellte Frage höchstwahrscheinlich gezeigt hätten – liegen sie aber „inhaltlich“ denkbar weit auseinander. Was aber, wenn ein Schüler die Frage „Term oder Therme?“ dahingehend beantworten sollte: „Ich habe mehr Lust auf Terme“ – ohne dabei wirklich die Badeanstalt zu meinen?! Ganz einfach. Dann hat dieser Schüler einfach mehr Spaß an Terme als auf Therme – und der Mathematik-Lehrer hat mit seiner gestellten Fangfrage alles richtig gemacht. Denn dadurch hat er bewiesen, dass Terme noch mehr Spaß machen können als Therme. Nun muss nur noch der Mathe-Lehrer auch alle anderen Schüler davon überzeugen…

Aufgaben zum Mathe-Stoffgebiet Term
1. Mathe-Nachhilfe-Aufgabe: Fasse folgende Terme so weit zusammen wie möglich!
a) 15x +17 + 23x – 17x – 22 + 39x – 13 + 17 – 49x
b) 3,2y + 7,3 – 2,4y + 9,4 – 10,5 + 2,3y + 12,8y – 14,8
c)
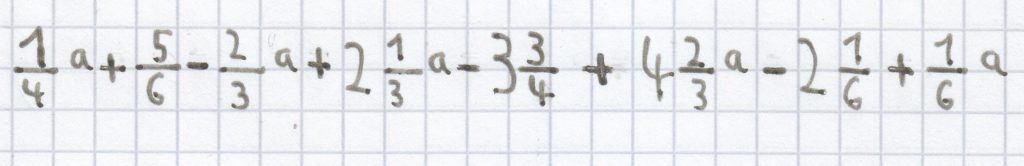
d) 18c + 12d – 3 – 12c + 3c – 12 + 4d –21c + 9 + 5 – 21d
e) s + s + s + s + s + t + t + t – s + t + t – t
f) fg + f – 2fg + f² – g² + 3f² + 9 + 12g² –11
2. Mathematik-Nachhilfe-Aufgabe: Untersuche, welche Terme noch vereinfacht werden können – und vereinfache diese!
a) 5b – 2 + b3
b) 9y – 23 + 3y²
c) 4abc – 12 cab + 2dab
d) 18a² + 13a + 3a³
3. Mathematik-Nachhilfe-Aufgabe: In allen Termumformungen steckt ein Fehler. Welcher Fehler wurde jeweils gemacht?
a) 5y – 5 = y
b) 5z + 9z² = 14 z²
c) 5c + 11b = 16bc
d) d³ + 12 = 12d³
e) 7ab – b = 7a
f) 9a² – 9a = 0
g) 12b² + 2b = 14b³
h) c³ – c² = c
i) abc – c = ab
4. Mathe-Nachhilfe-Aufgabe: Löse alle vorhandenen Klammern auf und fasse anschließend so weit wie möglich den Term zusammen.
a) 12a + (13b + 11 – 14a) + 7 – (23a – 35b – 19) + 4b – (–8 – 22b – 2a)
b) –(3,2y + 22x – 1,4z) – (22x – 1,4z + 2,3y) + (4,1x – 2,3y + 11z)
c) 2,9s + 3,5t + (3,9r) – (3,9r² – 4,2t + 3,5r) – (4 + 5,3r – 2,5s + t³)
5. Mathe-Nachhilfe-Aufgabe: Vielleicht auf den ersten Blick 6 verschiedene Terme! Nach dem richtigen Klammernauflösen und Zusammenfassen sind jedoch 2 absolut gleich!
a) –35 –7x + (38 + 8x)
b) (35 –7x) – (38 + 8x)
c) –35 + (7x –38 + 8x)
d) –(35 + 7x) – 38 + (–8x)
e) –(35 + 7x + 38) + 8x
f) –(35 + 7x + 38 + 8x)

Lösungen zum Mathe-Stoffgebiet Term
1. Lösung der Mathematik-Nachhilfe-Aufgabe: Zusammenfassen von Termen.
a) Zuerst ordnet man die Terme nach gleichen Einzeltermen:
15x + 23x – 17x + 39x– 49x + 17 – 22 – 13 + 17.
Dann fasst man zusammen: 11x – 1.
Weiter lässt sich der Term nicht vereinfachen.
b) Auch bei Einzeltermen, in denen Prozentzahlen vorkommen, ordnet man am besten zuerst alle zusammengehörigen Terme:
3,2y – 2,4y + 2,3y + 12,8y – 14,8 + 7,3 + 9,4 – 10,5.
Dann fasst man wiederum zusammen: 15,9y – 8,6.
Das ist der Endterm, da nicht weiter vereinfacht werden kann.
c) Ebenso wenn Einzelterme aus einer Bruchzahl bestehen, ordnet man diese anfangs:
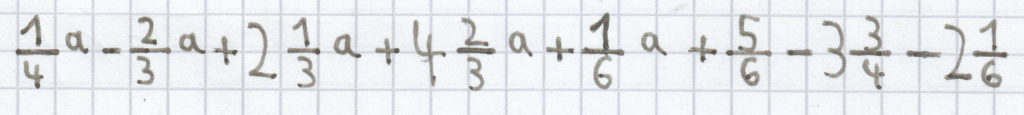
Daraufhin löst man die gemischten Brüche auf:
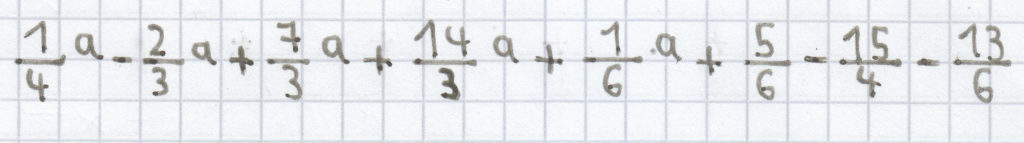
Dann macht man alle Brüche gleichnamig:
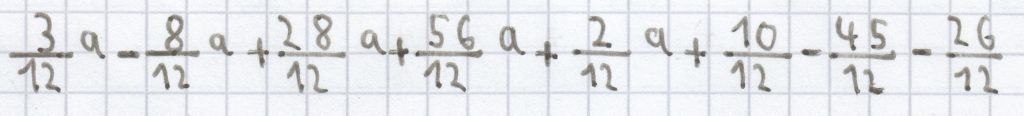
Jetzt kann man endlich die gleichartigen Einzelterme zusammenfassen:
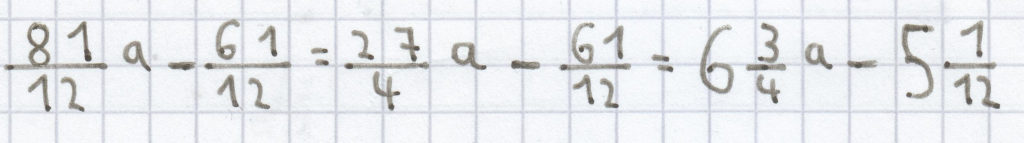
Das ist endlich der nicht mehr weiter zu vereinfachende Endterm.
d) Als erstes ordnet man wiederum den Term: 18c – 12c + 3c –21c + 12d + 4d – 21d – 3 – 12 + 9 +5.
Dann kann man die gleichartigen Einzelterme zusammenfassen: –21c – 5d – 1. Das ist schließlich der Endterm.
e) Der geordnete Term sieht hier wie folgt aus: s + s + s + s + s – s + t + t + t + t + t – t.
Jetzt kann ganz einfach zusammengefasst werden: 4s +4t.
Weiter kann der Term nicht mehr vereinfacht werden.
f) Zunächst ordnet man den Term wiederum: f² + 3f² + f + fg – 2fg – g² + 12g²+ 9 – 11.
Dann kann man wiederum zusammenfassen: 4f² + f – fg +11g² – 2.
Das ist schließlich der Endterm.
2. Lösung der Mathe-Nachhilfe-Aufgabe: Welcher Term kann noch vereinfacht werden, welcher nicht?
a) Dieser Term kann noch vereinfacht werden: 5b – 2 + b3. Denn anders geschrieben sieht der Term so aus: 5b – 2 + 3b. Hier gilt nämlich das Kommutativgesetz/Vertauschungsgesetz, das heißt, dass b3 = 3b ist. Daher ergibt sich hier als Endterm: 8b – 2.
b) Dieser Term kann nicht mehr vereinfacht werden: 9y – 23 + 3y². Denn alle Einzelterme unterscheiden sich jeweils und können deshalb nicht mehr weiter zusammengefasst werden.
c) Dieser Term kann noch vereinfacht werden: 4abc – 12 cab + 2dab. Hier gilt nämlich wiederum das Kommutativgesetz/Vertauschungsgesetz, das heißt, dass –12cab = –12abc und 2dab = 2abd ist. Daher ergibt sich folgender Term: 4abc – 12 abc + 2abd. Der Endterm ist dann: –8abc + 2abd.
d) Dieser Term kann nicht weiter vereinfacht werden: 18a² + 13a + 3a³. Denn die jeweiligen Einzelterme unterschieden sich jeweils und dürfen deshalb nicht weiter zusammengefasst werden.
3. Lösung der Mathe-Nachhilfe-Aufgabe: Welcher Fehler wurde bei der Termumformung jeweils gemacht?
a) 5y – 5 = y: Hier liegt der Fehler darin, dass die „nackte“ Zahl von dem Term 5y abgezogen wurde. Das ist algebraisch aber inkorrekt, da eine „nackte“ Einzelterm nie von einer Variablen mit Zahl abgezogen werden darf.
b) 5z + 9z² = 14 z²: Hier ist der Fehler, dass die beiden Variablen addiert wurden. Das ist aber algebraisch nicht korrekt, da die beiden Variablen verschiedene Potenzen vorweisen. Nur bei gleichen Potenzen dürfen gleiche Variablen addiert werden.
c) 5c + 11b = 16bc: Hier liegt der Fehler darin, dass zwei verschiedene Variablen samt Zahl zusammengefasst wurden. Das ist aber deshalb algebraisch falsch, da niemals verschiedenartige Variablen addiert oder subtrahiert werden dürfen.
d) d³ + 12 = 12d³: Hier ist der Fehler, dass der Einzelterm mit und der Einzelterm ohne Variable addiert wurden. Das ist aber algebraisch inkorrekt, da niemals eine Variable mit einer „nackten“ Zahlen zusammengefasst werden darf.
e) 7ab – b = 7a: Hier liegt der Fehler darin, dass der Einzelterm mit der einen Variable von dem Einzelterm mit den zwei Variablen abgezogen wurde. Das ist deshalb algebraisch inkorrekt, da niemals eine einzelne Variable von zwei Variablen subtrahiert werden darf. Ebenso darf sie niemals zu zwei Variablen addiert werden.
f) 9a² – 9a = 0: Hier ist der Fehler, dass nicht auf die verschiedenen Potenzen bei den Variablen Acht gegeben wurde. Algebraisch ist nur korrekt gleiche Variablen voneinander abzuziehen beziehungsweise miteinander zu addieren, wenn die Potenzen gleich sind.
g) 12b² + 2b = 14b³: Hier liegt der Fehler darin, dass bei den Einzeltermen die gleichen Variablen dahingehend zusammengefasst wurden, dass einfach die Potenzen addiert wurden. Das ist aber algebraisch inkorrekt, da niemals bei einer Addition oder Subtraktion die Potenzen gleicher Variablen addiert oder subtrahiert werden dürfen. Auch darf man gleiche Variable mit unterschiedlichen Potenzen sowieso nicht addieren oder voneinander abziehen.
h) c³ – c² = c: Hier liegt der gleiche Fehler vor wie in Aufgabe g), bloß dass hier die eine Potenz von der anderen abgezogen wird, bei Aufgabe g) wurde sie addiert.
i) abc – c = ab: Hier ist der Fehler, dass von einem Einzelterm, der aus drei verschiedenen Variablen besteht, einfach über eine Subtraktion eine abgezogen wird. Das ist aber deshalb algebraisch nicht richtig, da man durch Subtraktion niemals aus einem aus verschiedenen Variablen bestehenden Einzelterm einzelne Variablen herauslösen kann.
4. Lösung der Mathe-Aufgabe: Auflösen von Klammern und Zusammenfassen des Terms
a) Die erste Klammer kann man sofort auflösen, da hiervor ein Plus steht und deshalb alle Vorzeichen unverändert bleiben. Bei der 2. und 3. Klammer steht ein Minus davor, weswegen es sich hier um Minusklammern handelt. Um die beiden Klammern richtig aufzulösen, muss man hier jeweils alle Vorzeichen innerhalb der Klammer umdrehen, das heißt, dass aus „plus“ „minus“ wird und aus „minus“ „plus“. Nach Auflösen der Klammern sieht der Term „12a + (13b + 11 – 14a) + 7 – (23a – 35b – 19) + 4b – (–8 – 22b – 2a)“dann folgendermaßen aus:
12a + 13b + 11 – 14a + 7 – 23a + 35b + 19 + 4b + 8 + 22b + 2a = 12a – 14a – 23a + 2a + 13b + 35b + 4b + 22b + 11 + 7 + 19 + 8 = – 23a + 74b +45.
Weiter lässt sich der Term nicht mehr zusammenfassen.
b) Bei den ersten beiden Klammern handelt es sich um Minusklammern. Daher müssen hier alle Vorzeichen beim Auflösen der Klammer wiederum umgedreht werden. Bei der Plusklammer kann man die Klammer einfach wegnehmen. Der Term „–(3,2y + 22x – 1,4z) – (22x – 1,4z + 2,3y) + (4,1x – 2,3y + 11z)“ sieht dann wie folgt aus:
–3,2y – 22x + 1,4z – 22x + 1,4z – 2,3y + 4,1x – 2,3y + 11z = – 22x – 22x + 4,1x – 3,2y – 2,3y – 2,3y + 1,4z + 1,4z + 11z = –39,9x – 7,8y + 13,8z.
Das ist dann der Endterm.
c) Die erste Klammer des Terms ist hier eine Plusklammer, die beiden anderen sind Minusklammern. Daher kann man die erste Klammer sofort wegnehmen, bei den anderen beiden müssen jeweils alle Vorzeichen umgedreht werden. Der Term „2,9s + 3,5t + (3,9r) – (3,9r² – 4,2t + 3,5r) – (4 + 5,3r – 2,5s + t³)“ sieht dann folgendermaßen aus:
2,9s + 3,5t + 3,9r – 3,9r² + 4,2t – 3,5r – 4 – 5,3r + 2,5s – t³ = 3,9r – 3,5r – 5,3r – 3,9r² + 2,9s + 2,5s + 3,5t + 4,2t – t³ – 4 = – 4,9r – 3,9r² + 5,4s + 7,7t – t³ – 4
Das ist schließlich der Endterm.
5 Lösung der Mathe-Aufgabe: Welche beiden Terme sind nach dem Klammerauflösen und Zusammenfassen gleich?
a) –35 –7x + (38 + 8x) = –35 –7x + 38 + 8x = –7x + 8x –35 + 38 = x + 3
b) (35 –7x) – (38 + 8x) = 35 –7x – 38 – 8x = –7x – 8x + 35 – 38 = – 15x – 3
c) –35 + (7x –38 + 8x) = –35 + 7x –38 + 8x = 7x + 8x – 35 – 38 = 15x – 73
d) –(35 + 7x) – 38 + (–8x) = – 35 – 7x – 38 –8x = –7x – 8x – 35 – 38 = – 15x – 73
e) –(35 + 7x + 38) + 8x = – 35 – 7x – 38 + 8x = –7x + 8x – 35 – 38 = x – 73
f) –(35 + 7x + 38 + 8x) = – 35 – 7x – 38 – 8x = –7x – 8x – 35 – 38 = – 15x – 73
Wie man sieht, sind nur die beiden Endterme von d) und f) gleich.