1. Allgemeines zur Stereometrie

Die Stereometrie stellt ein Teilgebiet der Geometrie dar. Sie umfasst jegliche räumlichen Gebilde, die in der Mathematik als Körper bezeichnet werden. Das Entscheidende bei der Stereometrie ist daher, dass hier immer eine Dreidimensionalität vorliegt. Neben den Dimensionen Länge und Breite tritt hier immer auch mit einer Höhe bzw. Tiefe eine dritte Dimension auf – ansonsten entstehen ja kein Raum und auch keinerlei Körper. Die dritte Dimension, die Höhe bzw. Tiefe, ist daher das Hauptmerkmal der Stereometrie.
Im Fach Mathematik werden in der Stereometrie nun unterschiedliche Körper verschiedenartig untersucht. Das fängt mit den einfachsten Körpern an, dem Quader und dem Würfel, was beides sogenannte Prismen sind. Darauf werden noch andere Prismen näher betrachtet. Später kommen noch weitere Körper, wie die Kugel und der Zylinder, die Pyramide und der Kegel sowie der Pyramidenstumpf und der Kegelstumpf hinzu.
Im Mittelpunkt der Untersuchung verschiedenartiger Körper steht einerseits das Zeichnen der Körper sowie andererseits das Berechnen der Körper.
Zentral beim Zeichnen der verschiedenen Körper ist hierbei:
- das Schrägbild des jeweiligen Körpers korrekt zu zeichnen
Zentral bei der Berechnung bei verschiedenen Körpern ist dabei:
- die korrekte Berechnung des Volumens/Rauminhalts des jeweiligen Körpers
- die korrekte Berechnung der Oberfläche des jeweiligen Körpers
2. Das Schrägbild eines Körpers
Einen Körper stellt man zeichnerisch als sogenanntes Schrägbild dar. Das hat folgenden Grund: Ein Blatt hat nur zwei Dimensionen (nämlich Länge und Breite), ein Körper aber drei (Länge, Breite und Höhe/Tiefe). Daher kann man Körper nur auf eine bestimmte Weise zeichnerisch darstellen – und zwar mittels Schrägbild.
Beim Zeichnen eines Schrägbildes ist es wichtig, dass die Darstellung eines Körpers „verkürzt“ gezeichnet wird. Konkret heißt das, dass eine Dimension des Körpers immer mit dem Verkürzungsfaktor 0,5 gezeichnet wird und der Winkel dieser Dimension zur Waagrechten (des Blattes) 45° (diesen Winkel nennt man den „Verzerrungswinkel) beträgt. Seiten, die man von der Vorderansicht her nicht sieht bzw. die verdeckt sind, zeichnet man gestrichelt.
Die Dimension, die in der Regel „verkürzt“ mit dem Verkürzungsfatkor 0,5 gezeichnet wird, ist die Höhe/Tiefe. Das ist aber keine Pflicht: Auch die Länge und die Breite eines Körpers können stets „verkürzt“ gezeichnet werden. Je nach Aufgabenstellung muss man dies auch machen! Der Verzerrungswinkel beträgt immer 45º. Die gestrichelten verdeckten Seiten ergeben sich immer aus der Vorderansicht jedes Körpers.
2.1 Das Zeichnen eines Schrägbildes bei einem Körper
Ein viereckiges Prisma, ein Quader, weist folgendes Dimensionen auf: Länge 6 cm, Breite, 5 cm und Höhe 4 cm. Dieser Körper soll mittels Schrägbild gezeichnet werden.
1. Zeichenschritt:
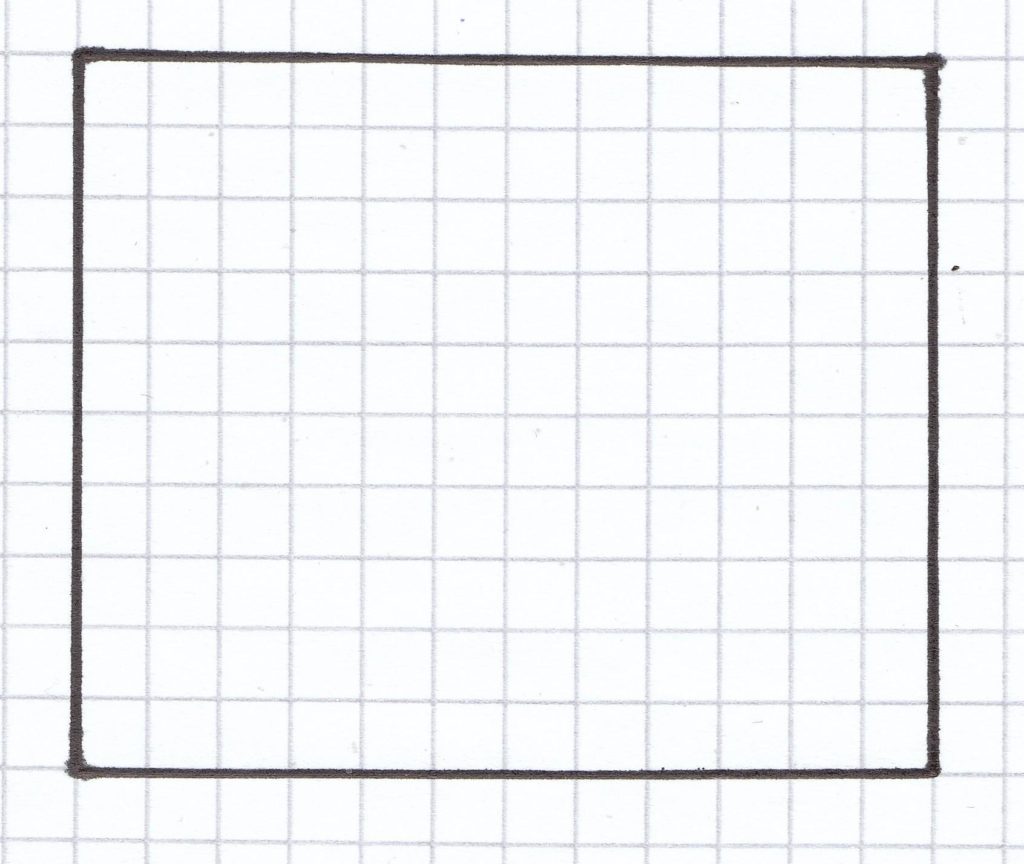
Als Erstes zeichnet man die Vorderfläche, die aus Länge und Breite besteht. Hier beträgt die Länge 6 cm und die Breite 5 cm. Um sich das Zeichnen des Körpers zu erleichtern, zeichnet man waagrecht und senkrecht entlang der Karos, auf dem karierten Blatt, das man hierfür benutzt.
2. Zeichenschritt:
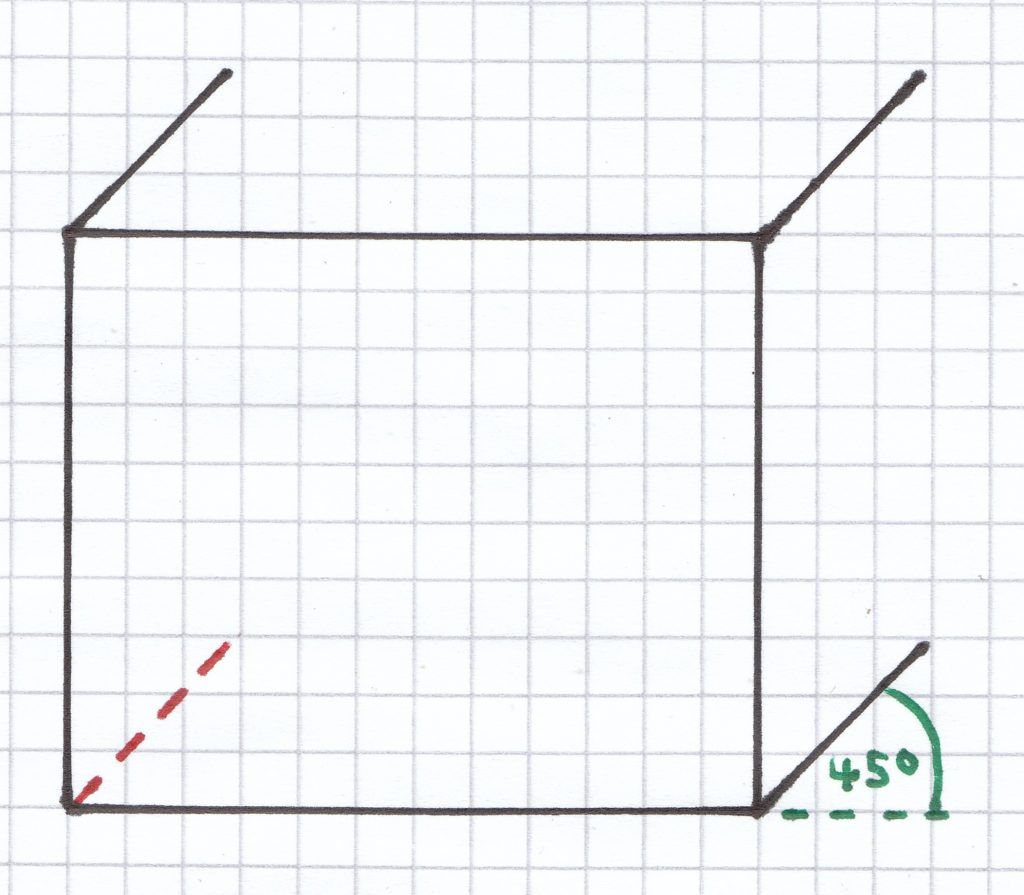
Als Nächstes zeichnet man alle nach hinten laufenden Seiten, die jeweils der Höhe des Körpers entsprechen. Da die Höhe „verkleinert“ wiedergegeben wird, beträgt diese hier 2 cm (4 cm mal 0,5 = 2 cm; Höhe mal Verkleinerungsfaktor). Die Höhe wird aber auch „verzerrt“ gezeichnet, das heißt unter einem Winkel von 45° zur Waagrechten (zur Grundseite des Körpers). Die nicht zu sehende bzw. verdeckte Seite des Körpers wird zudem gestrichelt gezeichnet.
3. Zeichenschritt:
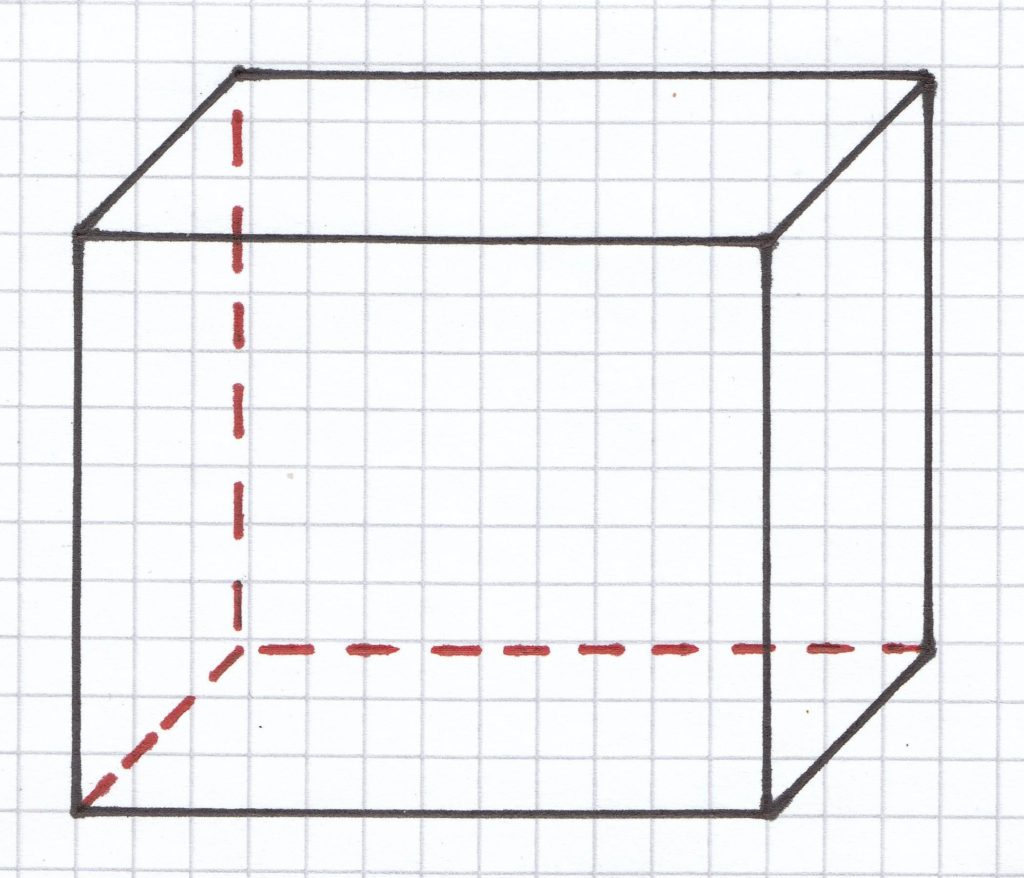
Als Letztes verbindet man alle Seiten miteinander. Dadurch zeichnet man die Rückflächen und die Seitenflächen des Körpers. Die nicht zu sehenden bzw. verdeckten Seiten zeichnet man gestrichelt.
Der Verzerrungswinkel muss nicht immer 45º betragen. Je nach Aufgabenstellung kann dieser auch eine andere Gradzahl vorweisen. Je nach Verzerrungsinwkel ändert sich hierbei die Darstellung des gezeichneten Körpers.
3. Die Berechnung eines Körpers
Bei der Berechnung eines Körpers sind die Berechnung des Volumens/Rauminhalts und der Oberfläche zentral. Unter Umständen muss auch die Mantelfläche der Körpers berechnet werden. Kann man aber die Obefläches des Körpers rechnerisch ermitteln, so kann man auch die Mantelfläche rechnerisch bestimmen, da diese ein Teil der Oberfläche darstellt.
3.1 Die Berechnung des Volumens/Rauminhalts eines Körpers
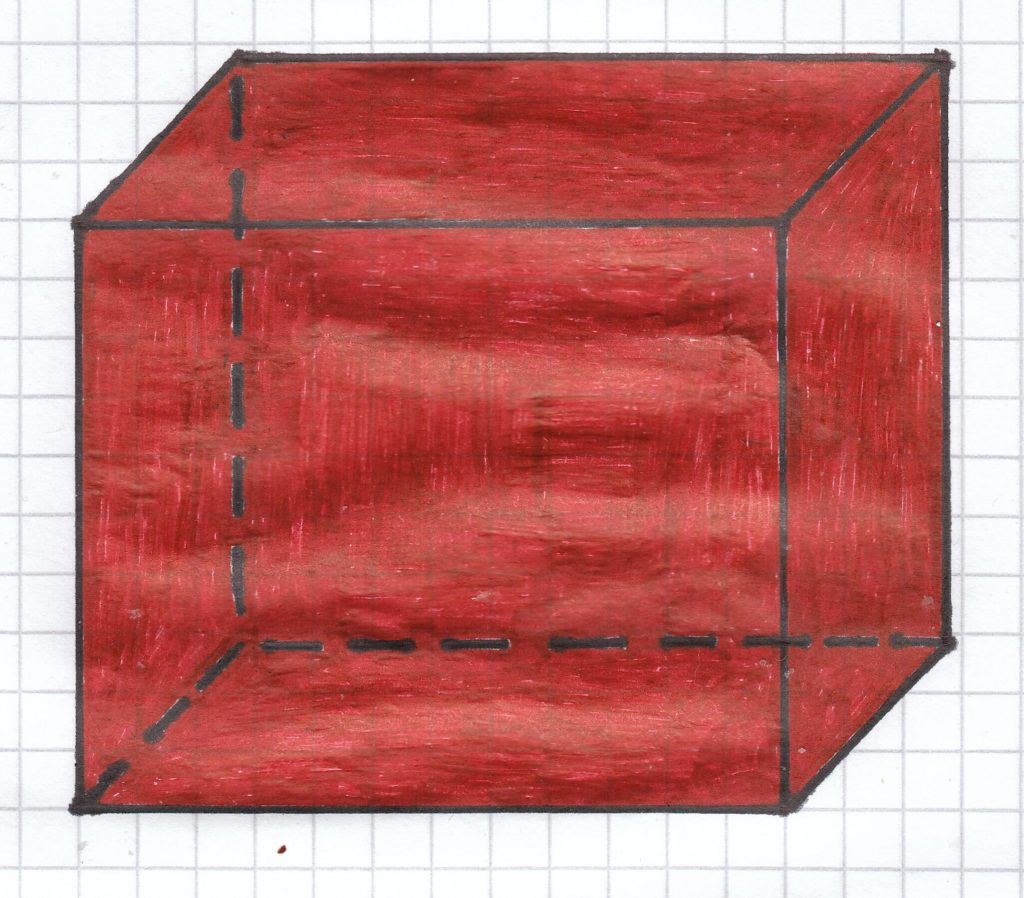
Bei der Berechnung des Volumens/Rauminhalts eines Körpers berechnet man gewissermaßen den kompletten Inhalt des Körpers. Am einfachsten kann man sich das vorstellen, wenn man einen Körper mit Wasser füllt, bis der Körper komplett mit Wasser voll ist. Der komplette mit Wasser gefüllte Inhalt des Körpers entspricht dann (in etwa, da die Dichte von Wasser ja nur bei 4° Celsius 1g/cm³ beträgt) dem Volumen/Rauminhalt des Körpers.
Die Berechnung der Volumens/Rauminhalt eines Körpers erfolgt im Fach Mathematik normalerweise anhand von bestimmten Körperberechnungsformeln.
3.2 Die Berechnung der Oberfläche eines Körpers
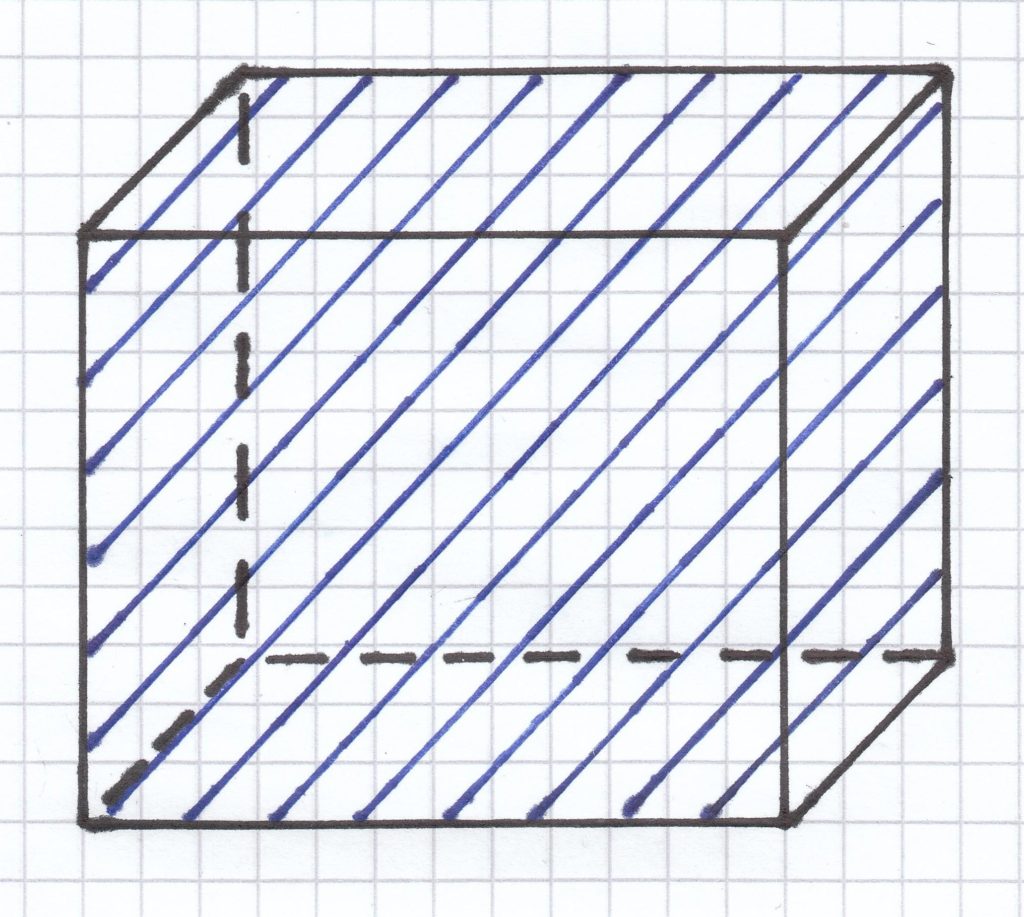
Die Oberfläche eines Körpers setzt sich aus allen Flächen eines Körpers zusammen. Bei diesem hier abgebildeten Körper sind das die Grundfläche, auf der dieser steht, die Deckfläche, die immer parallel zur Grundfläche die obige Fläche ist. Hinzu kommen die Vorderfläche und die Rückfläche sowie die beiden Seitenflächen rechts und links. Am einfachsten kann man sich merken, dass die Oberfläche aus allen Flächen besteht, die man mit der Hand anfassen kann.
3.3 Die Berechnung der Mantelfläche eines Körpers
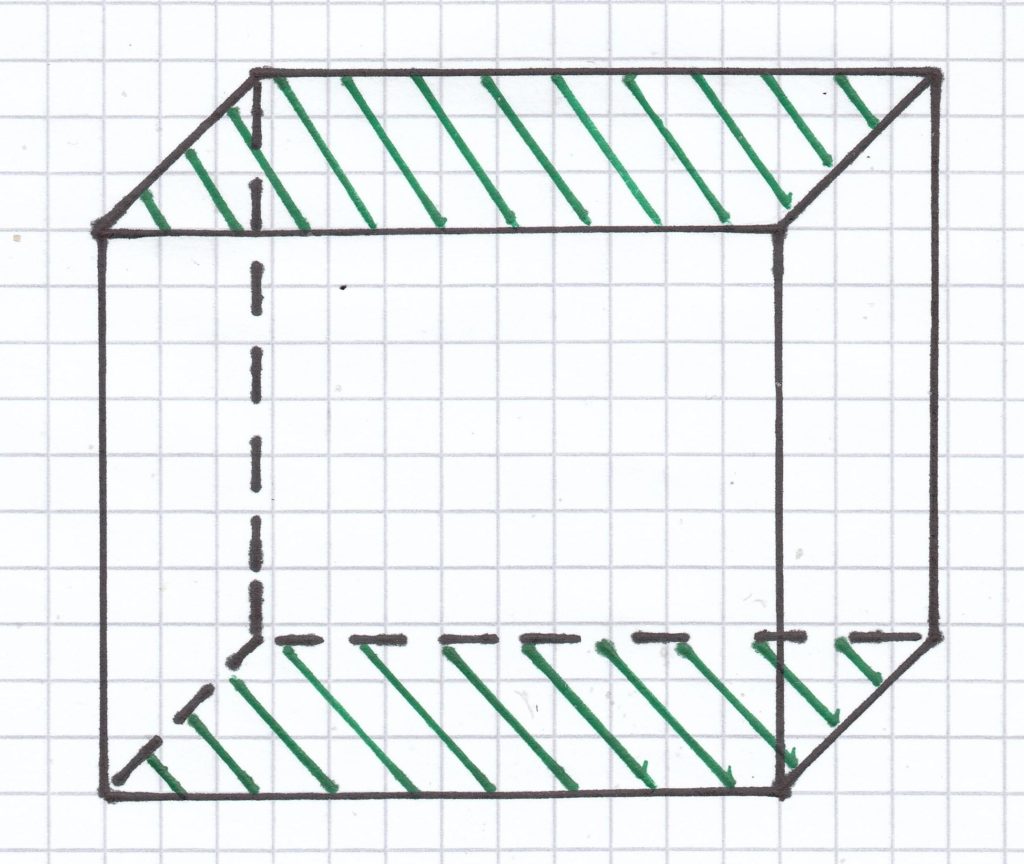
Die Mantelfläche stellt immer die Fläche eines Körpers dar – OHNE Grundfläche und Deckfläche. Bei diesem abgebildeten Körper setzt sich die Mantelfläche aus der Vorderfläche und der Rückfläche sowie den Seitenflächen rechts und links zusammen. Am einfachsten kann man sich merken, dass die Mantelfäche immer die Flächen eines Körper beinhaltet, die um den Köper herum anfassbar sind.