1. Allegemeines zum Gleichsetzungsverfahren
Bei diesem Lösungsverfahren eines linearen Gleichungssystems (LGS) steht das Gleichsetzen zweier Gleichungen im Mittelpunkt.
Zum Lösen eines linearen Gleichsetzungsverfahren mittels des Gleichsetzungsverfahren kann man drei verschiedene Wege heranziehen.
a) Man löst das LGS jeweils nach der Variablen x hin auf
b) Man löst das LGS jeweils nach der Variablen y hin auf
c) Man löst das LGS jeweils nach einer gemeinsamen Variablen mit gemeinsamen Faktor hin auf
2. Erster Lösungsweg mittels des Gleichsetzungsverfahrens
Der erste Lösungsweg eines LGS mittels des Gleichsetzungsverfahren beinhaltet hier zunächst das Auflösen beider Gleichungen nach dem Term x hin, um die nach x hin aufgelösten Gleichungen darauf gleichzusetzen.
I. 4x – 3y = 4
II. 4x – 5y = 20
Beide Gleichungen werden zuerst nach der Variablen x hin umgeformt.
I. 4x – 3y = 4 | + 3y
II. 4x – 5y = 20 | + 5y
I. 4x = 4 + 3y | : 4
II. 4x = 20 + 5y | : 4
I. x = 1 + 0,75y
II. x = 5 + 1,25y
Darauf setzt man beide nach x hin aufgelöste Gleichungen miteinander gleich.
I. = II. 1 + 0,75y = 5 + 1,25 y
Anschließend löst man die Gleichung nach y hin auf.
I. = II. 1 + 0,75y = 5 + 1,25 y | – 0,75y
I. = II. 1 = 5 + 0,5 y | – 5
I. = II. –4 = 0,5y | : 0,5
I.= II. –8 = y
Die sich ergebende Lösungskoordinate setzt man nun in eine der beiden Ursprungsgleichungen ein.
I. 4x – 3 · (–8) = 4
Darauf löst man die Gleichung nach x hin auf.
I. 4x – 3 · (–8) = 4
I. 4x + 24 = 4 | – 24
I. 4x = –20 | : 4
I. x = –5
Die Probe bestätigt die Lösung des LGS.
I. 4 · (–5) – 3 · (–8) = 4
II. 4 · (–5) – 5 · (–8) = 20
I. –20 + 24 = 4
II. –20 + 40 = 20
I. 4 = 4
II. 20 = 20
Die Lösungsmenge des LGS.
L = {–5 | –8}
3. Zweiter Lösungsweg mittels des Gleichsetzungsverfahrens
Der zweite Lösungsweg mittels des Gleichsetzungsverfahren beinhaltet hier zunächst das Auflösen beider Gleichungen nach dem Term y hin, um anschließend die nach y hin aufgelösten Gleichungen gleichzusetzen.
I. 4x – 3y = 4
II. 4x – 5y = 20
Beide Gleichungen löst man nach dem Term y hin auf.
I. 4x – 3y = 4 | – 4x
II. 4x – 5y = 20 | – 4x
I. –3y = 4 – 4x | : (–3)
II. –5y = 20 – 4x | : (–5)
I.
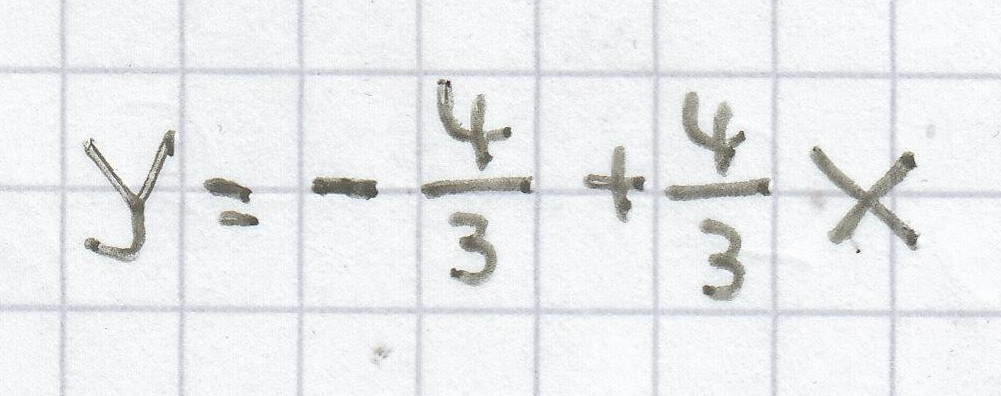
II. y = –4 + 0,8x
Darauf setzt man beide nach y hin aufgelöste Gleichungen gleich.
I. = II.

Die Gleichung löst man anschließend nach x hin auf.
I. = II.
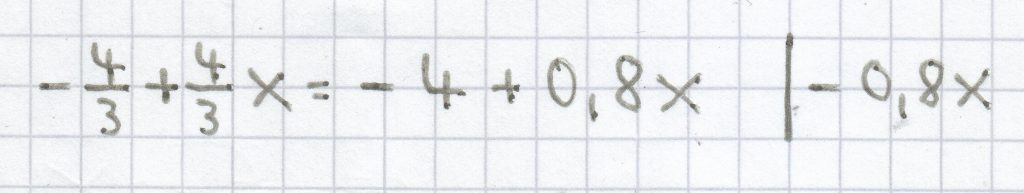
I. = II.

I. = II.

I. = II. x = –5
Die ermittelnde Lösungskoordinate setzt man in eine der beiden Ursprungsgleichungen ein.
I. 4 · (–5) – 3y = 4
Die Gleichung löst man dann nach y hin auf.
I. 4 · (–5) – 3y = 4
I. –20 – 3y = 4 | + 20
I. –3y = 24 | : (–3)
I. y = –8
Die Probe bestätigt die Lösung des LGS.
I. 4 · (–5) – 3 · (–8) = 4
II. 4 · (–5) – 5 · (–8) = 20
I. –20 + 24 = 4
II. –20 + 40 = 20
I. 4 = 4
II. 20 = 20
Die Lösungsmenge des LGS.
L = {–5 | –8}
4. Dritter Lösungsweg mittels des Gleichsetzungsverfahrens
Der dritte Lösungsweg mittels des Gleichsetzungsverfahrens sieht vor, gleiche Variablen mit gleichem Faktor gleichzusetzen.
I. 4x – 3y = 4
II. 4x – 5y = 20
Die erste Gleichung und die zweite Gleichung haben mit „4x“ jeweils die gleiche Variable mit dem gleichen Faktor. Wenn man nun die anderen Variable separiert, kann man daher die beiden Gleichungen miteinandere gleichsetzen.
I. 4x – 3y = 4 | + 3y
II. 4x – 5y = 20 | + 5y
I. 4x = 4 + 3y
II. 4x = 20 + 5y
Beide Gleichungen setzt man nun gleich, indem man die beiden Terme „4 + 3y“ „20 +5y“ miteinander gleichsetzt.
I. = II. 4 + 3y = 20 + 5y
Anschließend löst man die Gleichung nach y hin auf.
I. = II. 4 + 3y = 20 + 5y | – 3y
I. = II. 4 = 20 + 2y | – 20
I. = II. –16 = 2y | : 2
I. = II. –8 = y
Die Lösung setzt man in eine der beiden Ursprungsgleichungen ein, um die andere Lösungskoordinate zu erhalten.
I. 4x – 3 · (–8) = 4
I. 4x + 24 = 4 | – 24
I. 4x = –20 | : 4
I. x = –5
Die Probe bestätigt die Lösung des LGS.
I. 4 · (–5) – 3 · (–8) = 4
II. 4 · (–5) – 5 · (–8) = 20
I. –20 + 24 = 4
II. –20 + 40 = 20
I. 4 = 4
II. 20 = 20
Die Lösungsmenge des LGS.
L = {–5 | –8}
5. Vorgehensweise zum Lösen eines linearen Gleichungssystems mittels des Gleichsetzungsverfahrens
Bei einem Lösen eines LGS mittels Gleichsetzungsverfahren geht man folgendermaßen vor.
- Zuerst löst man beide Gleichungen des LGS nach einem Term hin auf, nach x oder y oder 4x.
- Darauf setzt man beide nach einem Term hin aufgelösten Gleichungen miteinander gleich. Die andere Gleichung behält man normalerweise bei. Man kann diese aber auch erst am Ende, wenn man die erste Lösungskoorndiate ermittelt hat, wieder aufgreifen.
- Die sich ergebende Gleichung mit einer Variablen löst man nach der Variablen hin auf. Dadurch erhält man eine Lösungskoordinate.
- Die ermittelnde Lösungskoordinate setzt man in eine der beiden Ursprungsgleichungen ein.
- Die Probe bestätigt die Lösung des LGS.
- Die Lösungskoordinaten ergeben die Lösungsmenge des LGS.