Die Terminologie in Mathematik ist sehr wichtig. Was? Die Terminologie! Was? Das Fachvokabular ? Was? Das Fachvokabular? Was? Die speziellen Wörter, die man im Fach Mathematik verwendet! Ach so! Versteht man wirklich gleich so oft bei bestimmten/speziellen Wörtern, die im Mathe-Unterricht gebräuchlich sind, BAHNHOF, dann sollte man schleunigst diesbezüglich seine überfälligen Hausaufgaben nachholen. Dann hat man nämlich schon Lücken im Fach Mathematik aufgebaut, die das Verständnis des weiteren dort behandelnden Lernstoffes erschweren. Ein Beispiel gefällig: Schüler und Schülerinnen müssen beispielsweise wissen, was ein Parameter ist (was schon wirklich gut ist, ist: Wenn man auch den eher selten verwendeten Fachbegriff bzw. Fachwort Formvariable kennt 😉 ). Nur dann kann man sich ja auch etwas unter diesem Fachvokabular vorstellen – und schließlich gezielt eine Aufgabe lösen!
Aufgaben zum Mathe-Stoffgebiet Formvariablen
1. Mathematik-Nachhilfe-Aufgabe: Gib die Lösungsmenge der Gleichung an. Hierbei ist x die Lösungsvariable.
a) sx – r = 0
b) m – n = 8(x + n)
c) 5y – x = 4x – y
d) sx = t + 4 für (x ≠ 0)
2. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Gleichung. x ist hierbei die Lösungsvariable.
a)
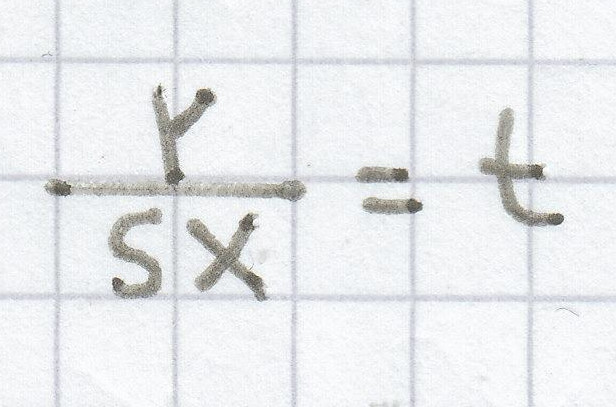
b)
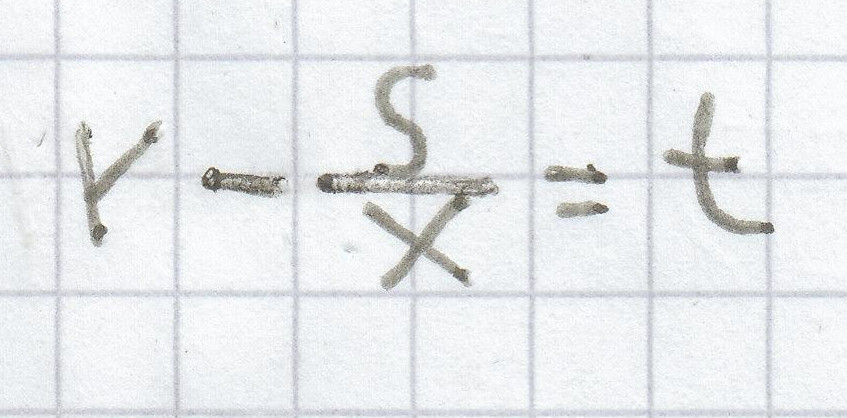
c)
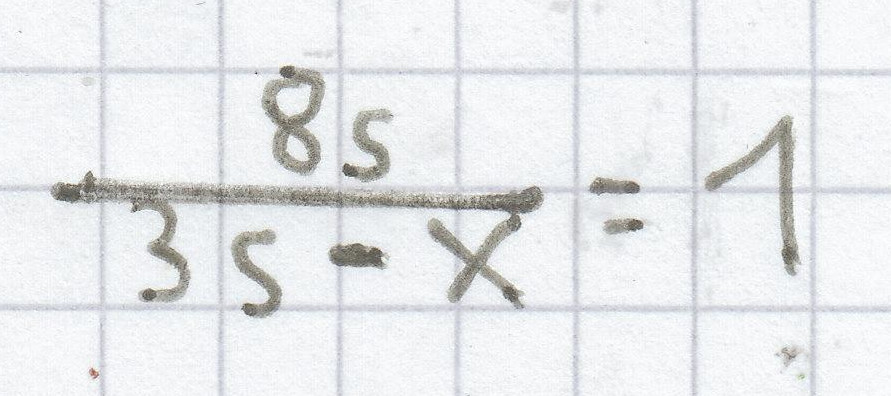
d)
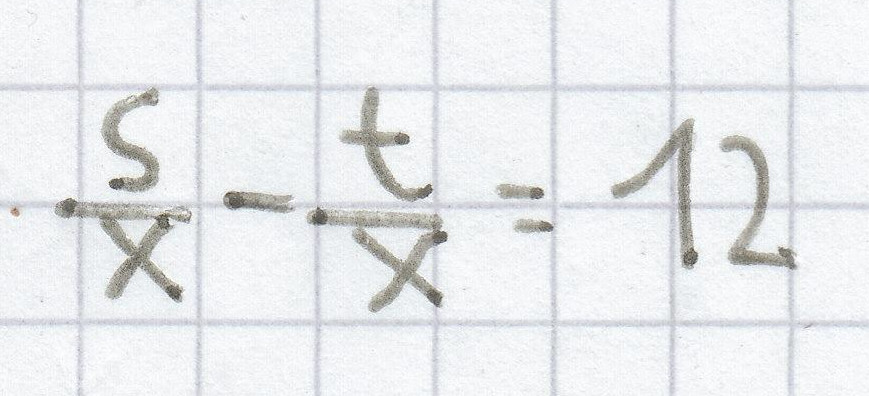
3. Mathematik-Nachhilfe-Aufgabe: Gib an, für welchen Wert der Formvariablen die Gleichung

folgende Lösungen hat.
a) L = {4}
b) L = { } bzw. L = Ø
c) L = ℚ \ {1}
d) L = {–6}
4. Mathe-Nachhilfe-Aufgabe: Jede Gleichung soll nach der dort vorkommenden Variable hin aufgelöst werden. Was muss über eine mögliche Formvariable gesagt werden?
a) rx + x = t
b) rx + rs = st
c) rx + sx = t
d) r + sx = t

Lösungen zum Mathematik-Stoffgebiet Gleichungen mit Parametern
1. Mathe-Nachhilfe-Aufgabe: Löse die Gleichung nach der Lösungsvariablen hin auf. x ist die Lösungsvariable.
a)
sx – r = 0 | + r
sx = r | : s
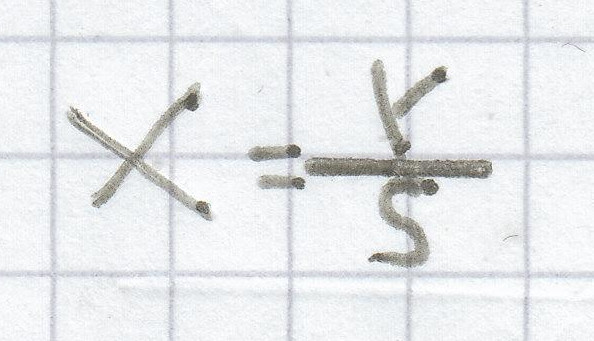
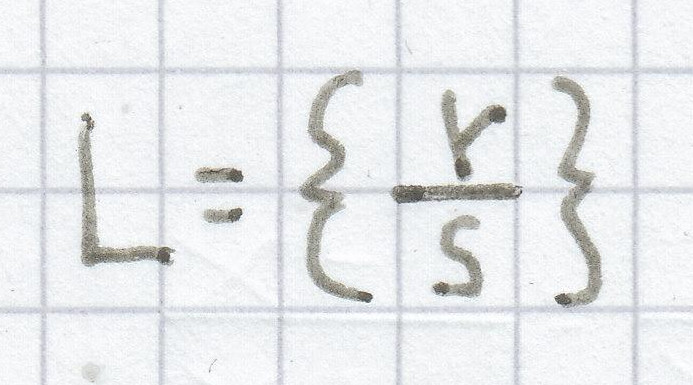
b)
m – n = 8(x + n)
m – n = 8x + 8n | – 8n
m – 9n = 8x | : 8
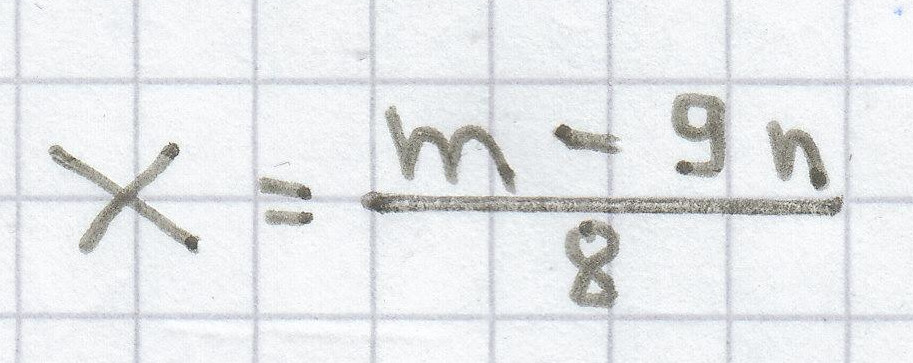

c)
5y – x = 4x – y | + x
5y = 5x – y | + y
6y = 5x | : 5
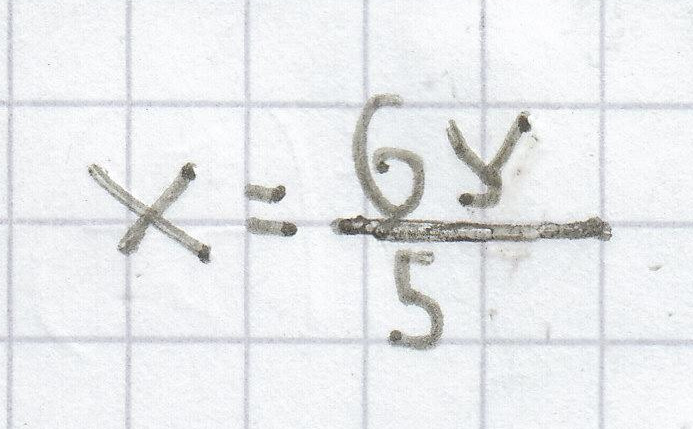

d)
sx = t + 4 für (x ≠ 0)
sx = t + 4 | : s
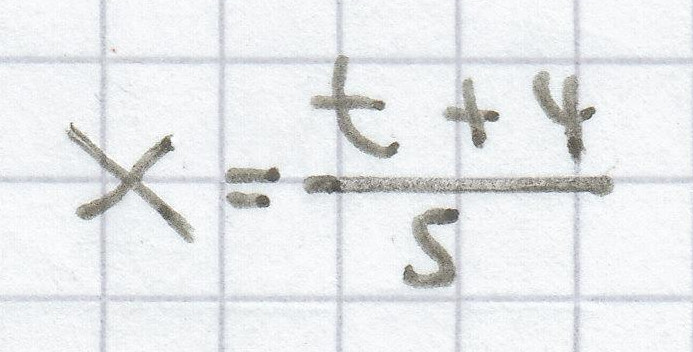
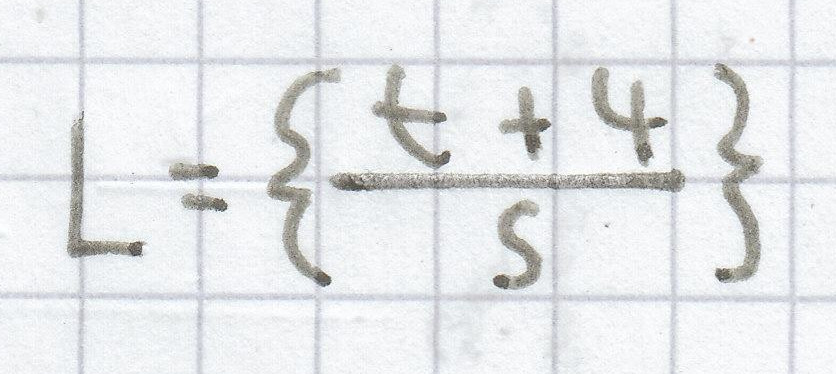
2. Mathematik-Nachhilfe-Aufgabe: Ermittle für die Gleichung die Lösungsmenge. Die Lösungsvariable ist hierbei x.
a)
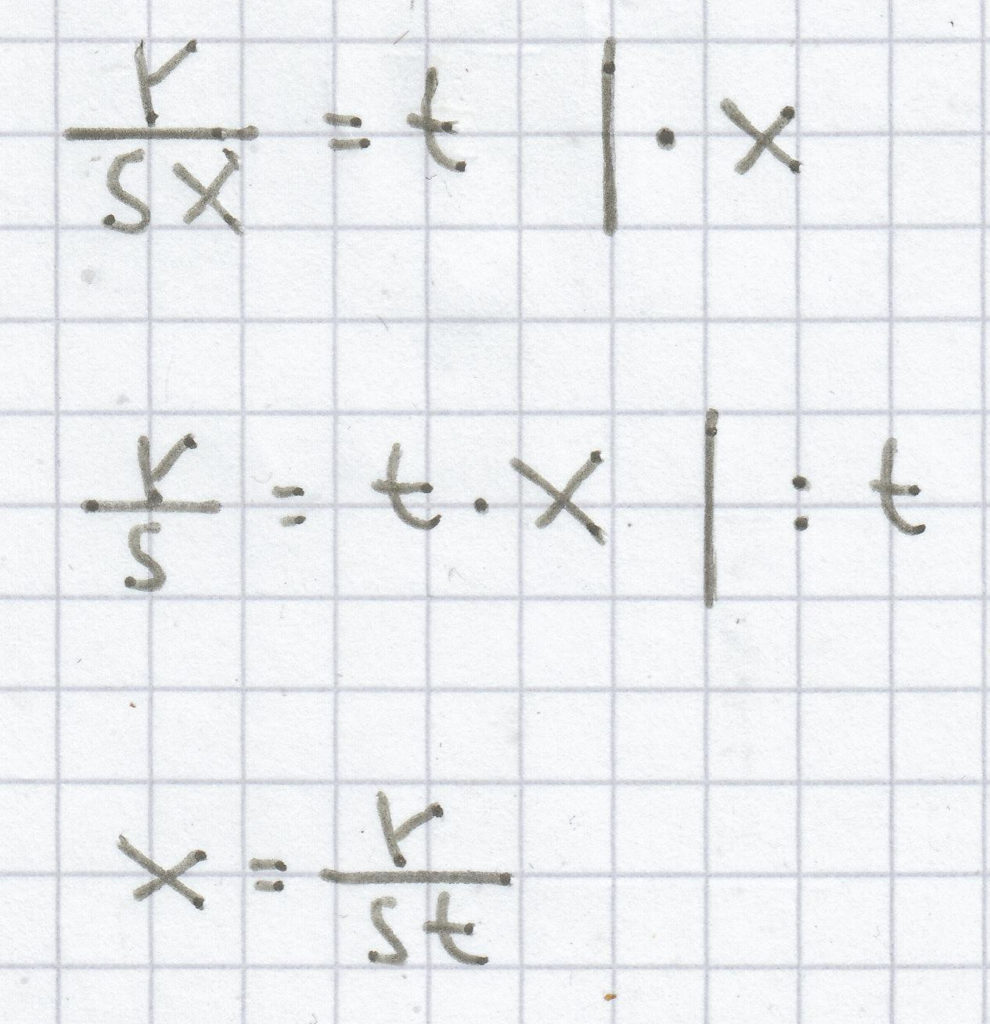
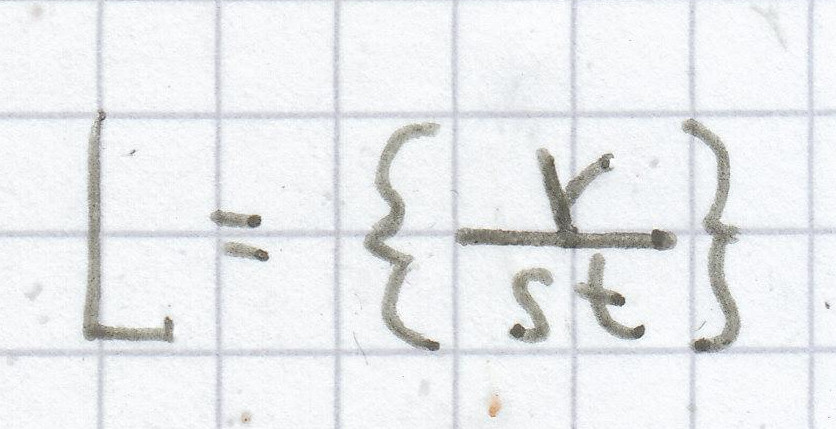
b)
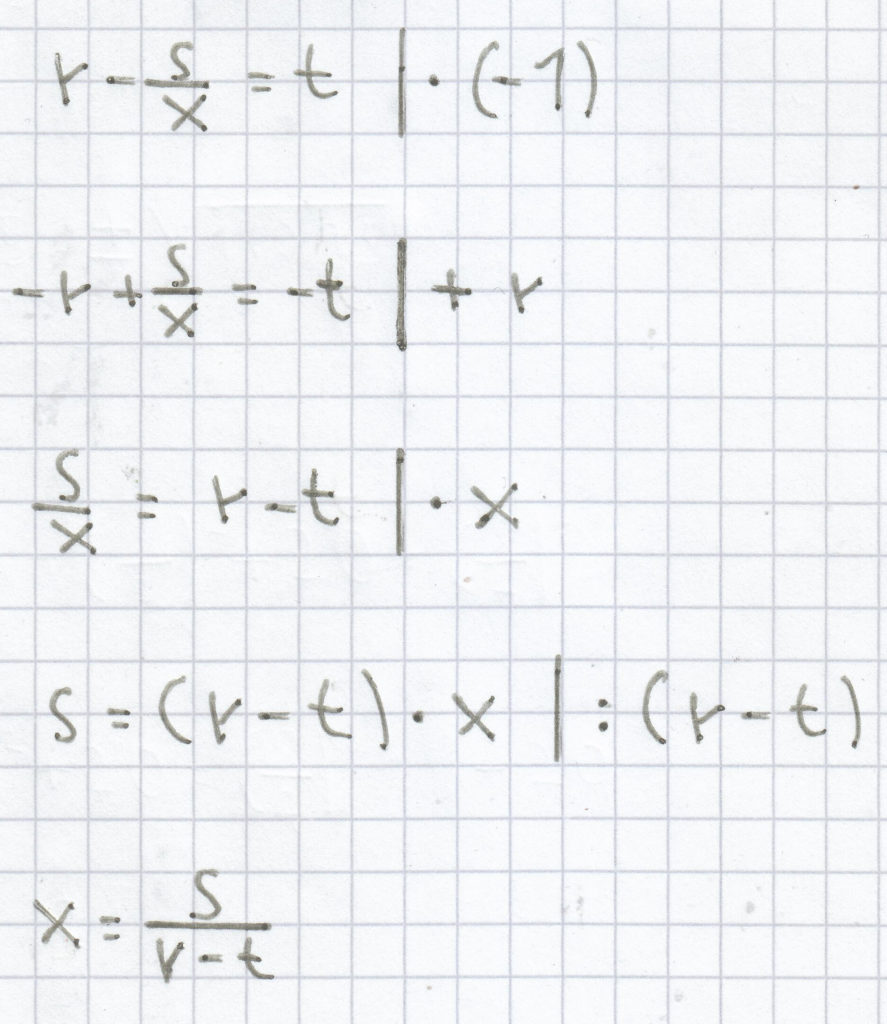
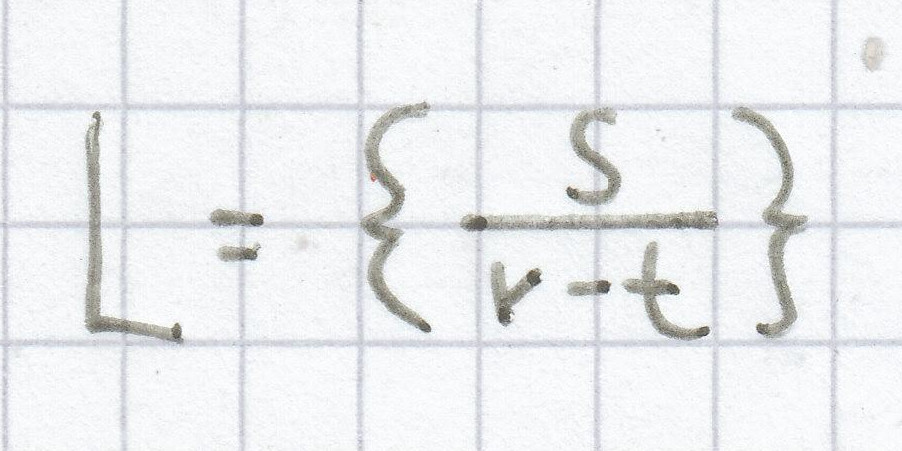
c)

8s = 1 · (3s – x)
8s = 3s – x | – 3s
5s = –x | · (–1)
x = –5s
L = {–5s}
d)
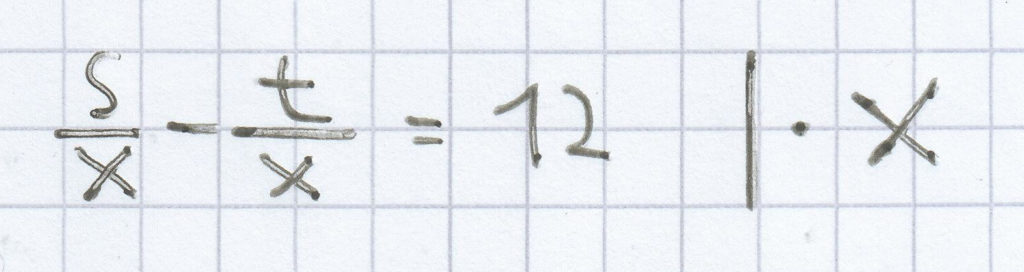
s – t = 12x | : 12
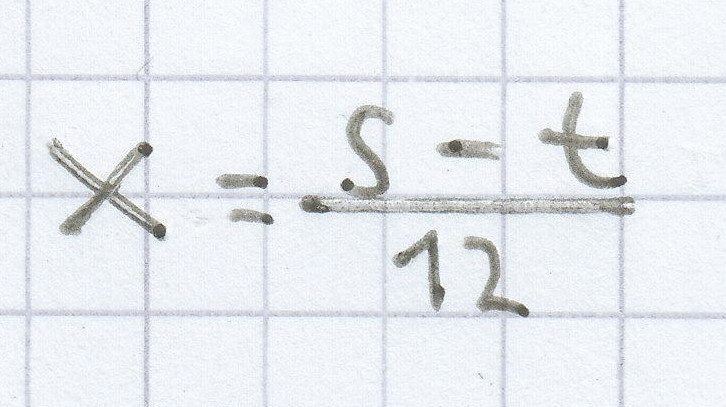
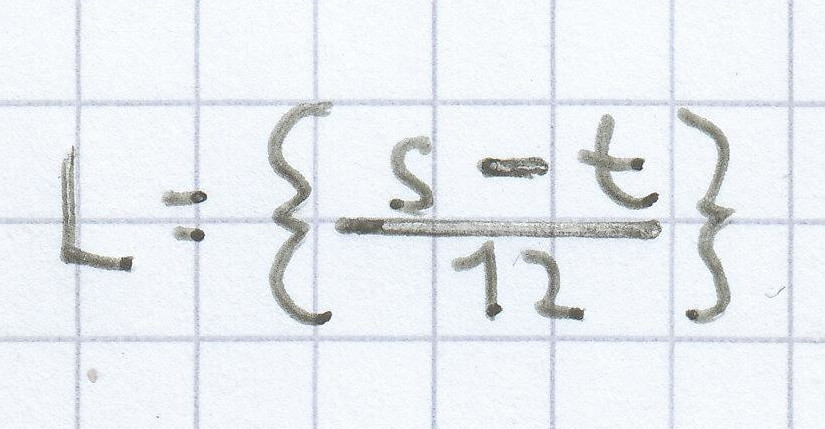
3. Mathe-Nachhilfe-Aufgabe: Bestimme zu der Gleichung

, die folgende Lösungen hat, jeweils die Formvariable.

für x ≠ –s und x ≠ 0
a) L = {4}
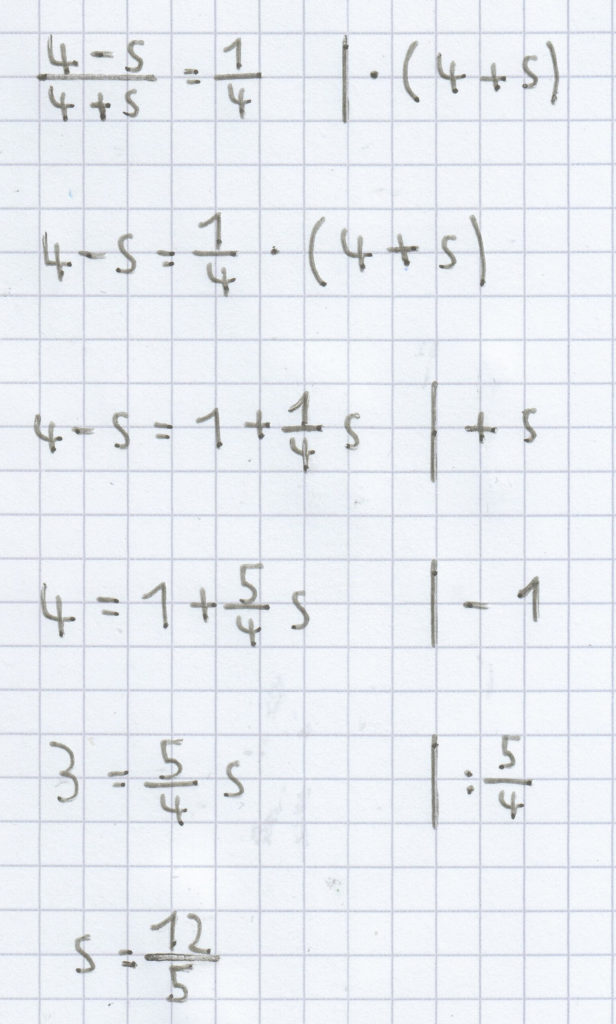
b) L = { } bzw. L = Ø
Hier muss mann sich überlegen, wann liefert die Gleichung mit Formvariable keine Lösung. Das ist der Fall, wenn der eine Nenner im Bruchterm mit der Formvariable gleich null wird. Hieraus ergibt sich:
x + s = 0 | – s
x = –s
c) L = ℚ \ {1}
Hier kann man sich zunächst überlegen, wann die Gleichung bei der Zahl 1 nicht definiert ist. Das ist der Fall, wenn bei dem ersten Bruchterm im Nenner die Zahl –1 steht. Also muss hier der Parameter –1 sein. Jetzt muss sich bei diesem Parameter auch noch links und rechts des Gleichheitszeichens die Zahl 0 ergeben, damit die obige Lösung herauskommt.
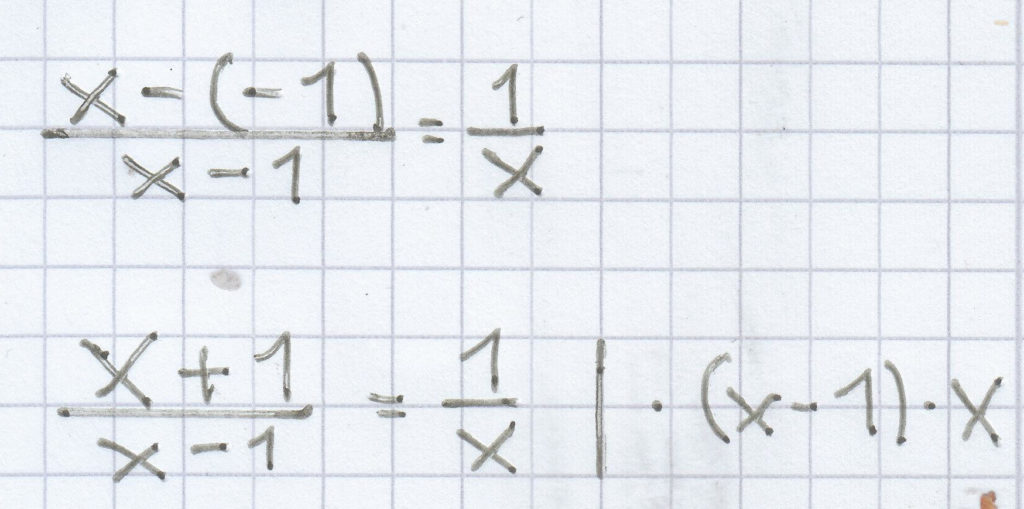
(x + 1) · x = 1 · (x – 1)
x² + x = x – 1
Hier sieht man bereits, dass die Gleichung nicht die obige Lösung ergibt.
x² + x = x – 1 | – x
x² = – 1 | √
x = n. d. (nicht definiert)
Auch weiter bestätigt sich, dass die Gleichung nicht die obige Lösung ergibt. Die angebene Lösung der Aufgabe c) ist daher unter dieser Gleichung mit Parametern nicht möglich.
Aber man kann auch die Überlegung heranziehen, dass beide Seiten der Gleichung auf jeden Fall die Zahl 0 ergeben müssen. Ansonsten kann ja die Lösung nicht erfüllt werden.
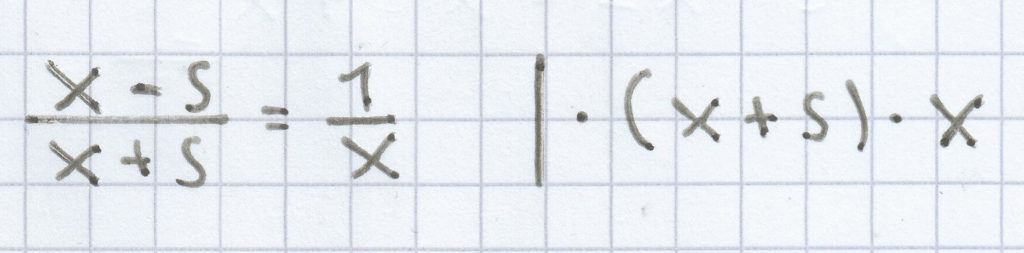
(x – s) · x = 1 · (x + s)
x – s = 0 oder x = 0 und x + s = 0
x = s oder x = 0 und x = –s
Auch hier zeigt sich, dass man keine Möglichkeit findet, dass die Gleichung gleich null wird. Daher findet man kein Ergebnis, das die Aufgabe c) erfüllt.
d) L = {–6}
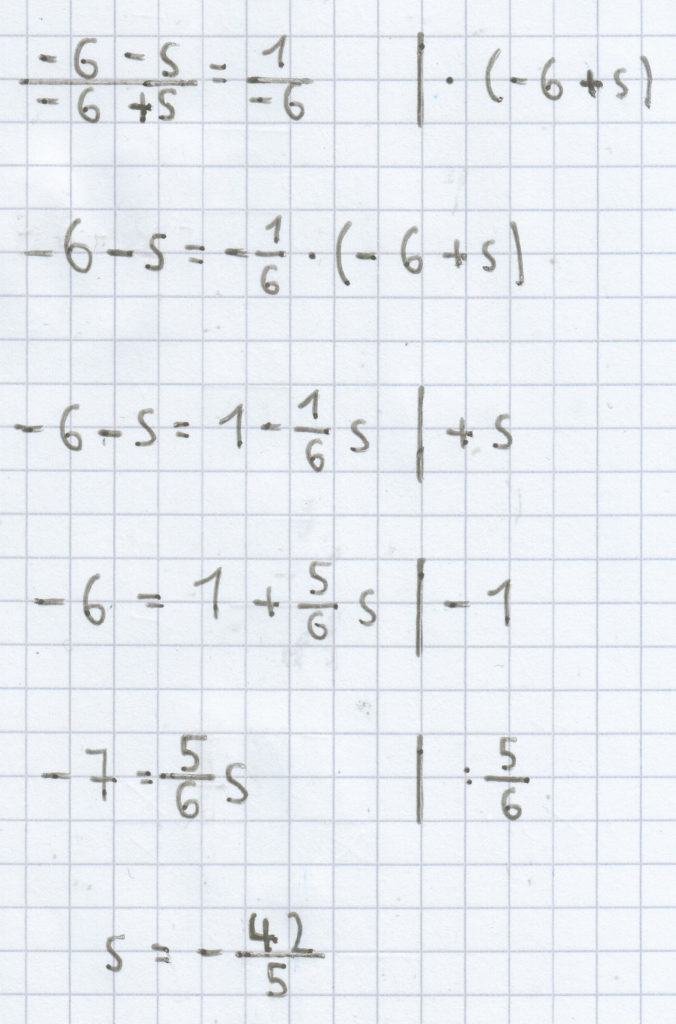
4. Mathematik-Nachhilfe-Aufgabe: Die Gleichung soll jeweils nach der dort vorkommenden Variablen hin aufgelöst werden. Welche Aussagen muss man über eine Formvariable machen?
a) rx + x = t
x ist die Lösungsvariable:
rx + x = t
x · (r + 1) = t | : (r + 1)
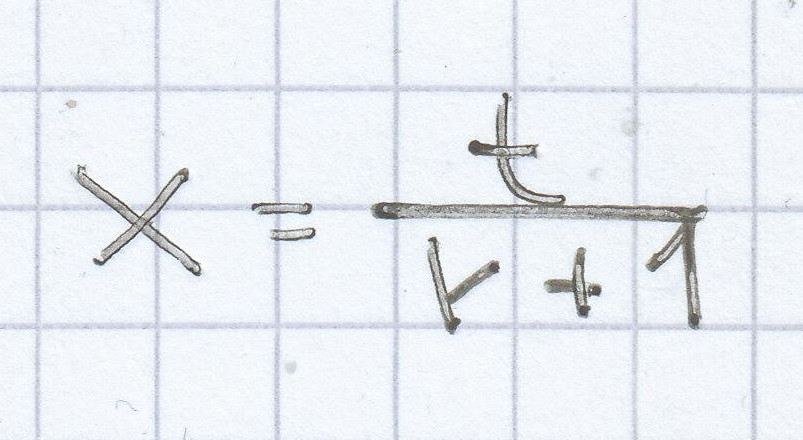
für r ≠ –1
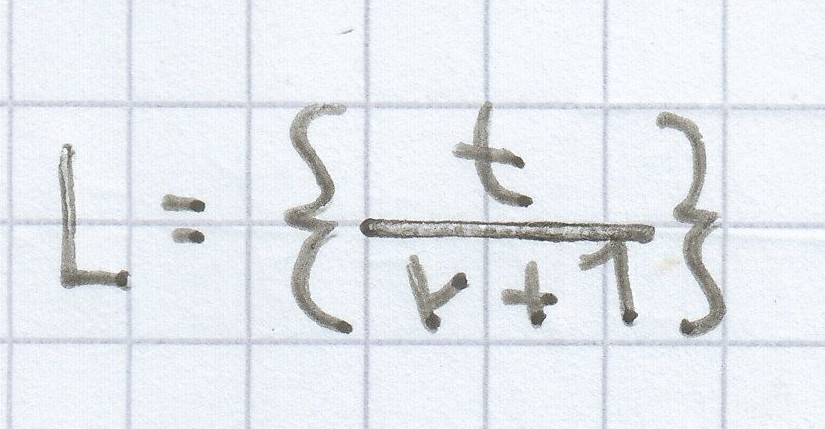
r ist die Lösungsvariable:
rx + x = t | – x
rx = t – x | : x
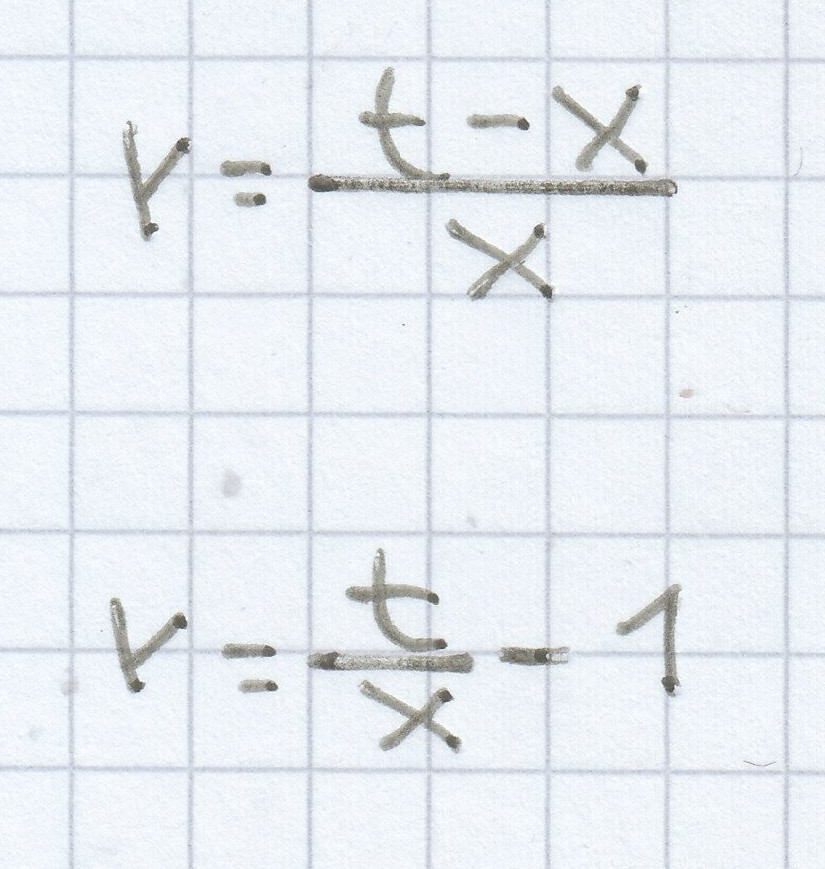
für x ≠ 0

t ist die Lösungsvariable:
rx + x = t
t = rx + x
L = {rx + x}
b) rx + rs = st
r ist die Lösungsvariable:
rx + rs = st
r · (x + s) = st | : (x + s)
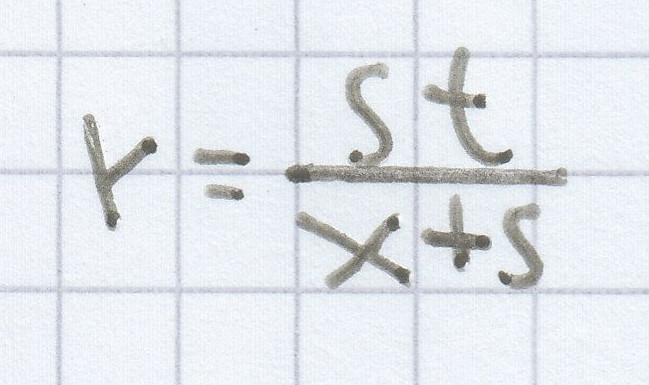
für x ≠ –s bzw. s ≠ –x
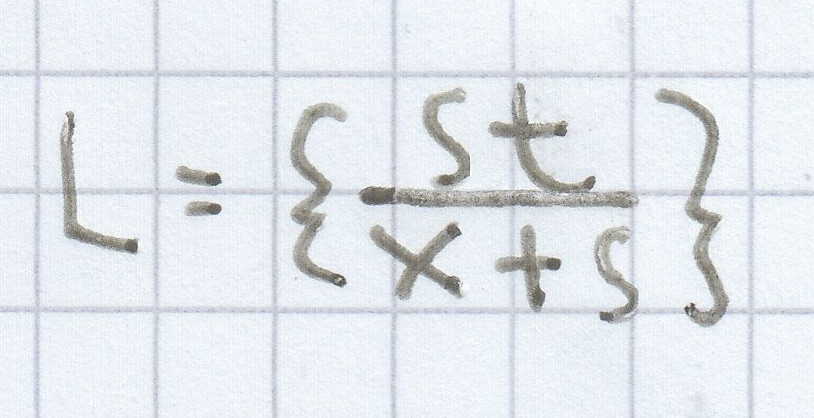
s ist die Lösungsvariable:
rx + rs = st | – rs
rx = st – rs
rx = s · (t – r) | : (t – r)
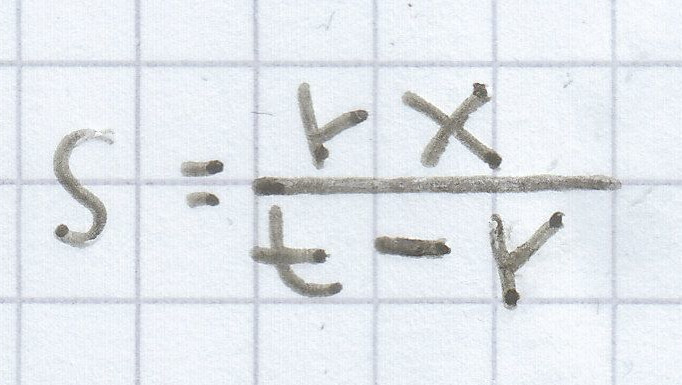
für r ≠ t
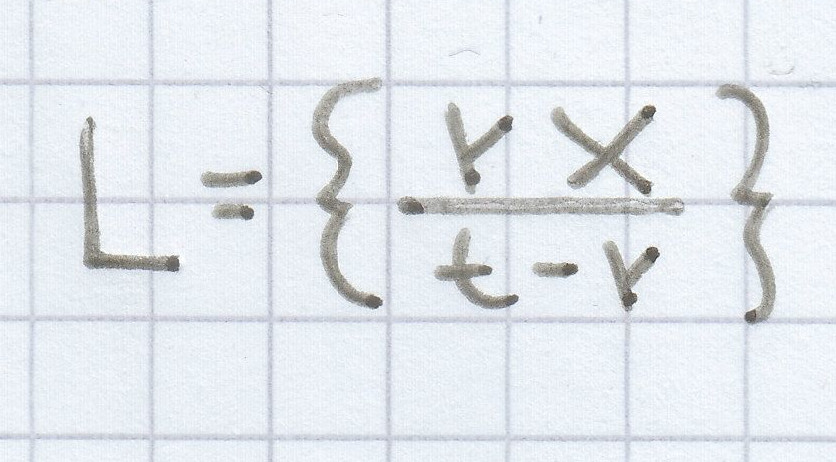
x ist die Lösungsvariable:
rx + rs = st | – rs
rx = st – rs | : r
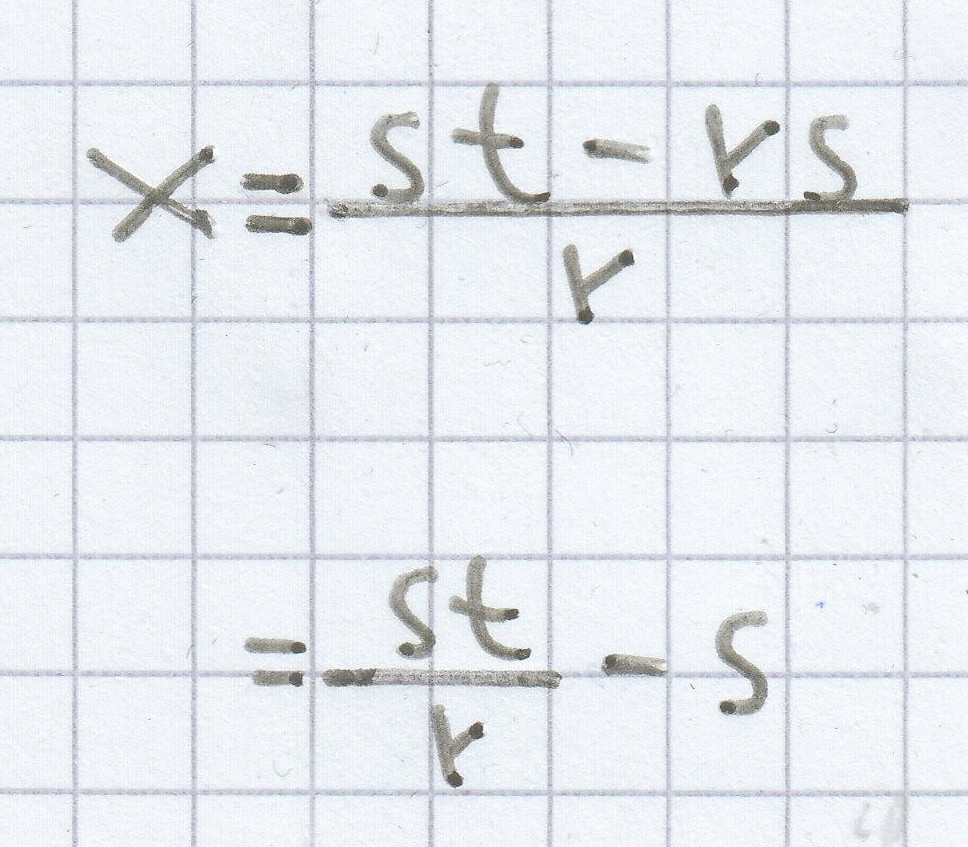
für r ≠ 0

c) rx + sx = t
r ist die Lösungsvariable:
rx + sx = t | – sx
rx = t – sx | : x
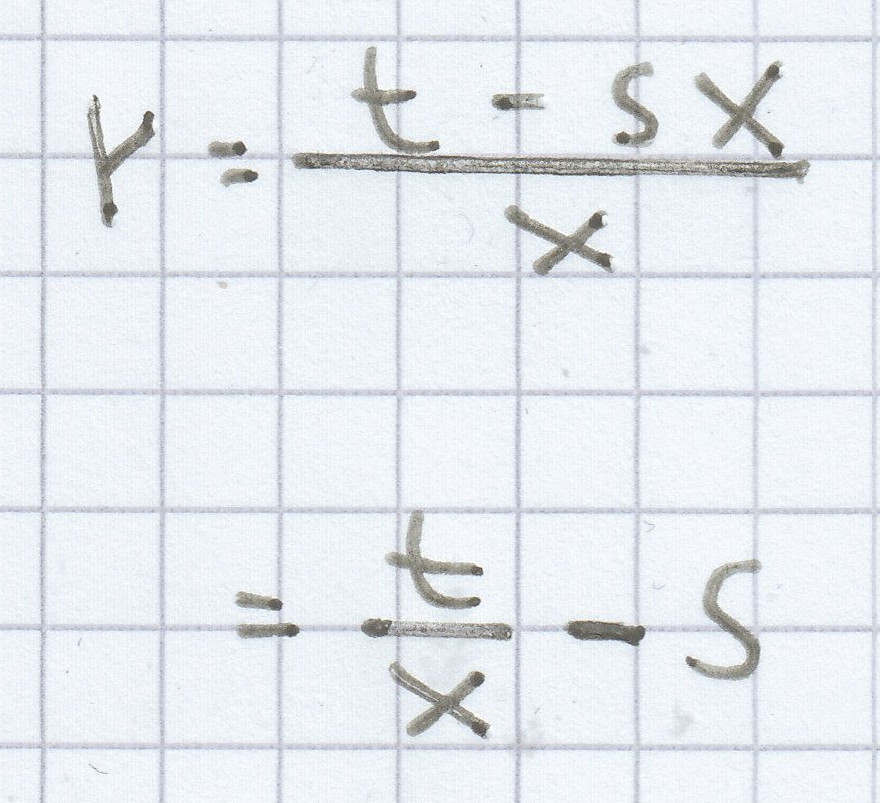
für x ≠ 0
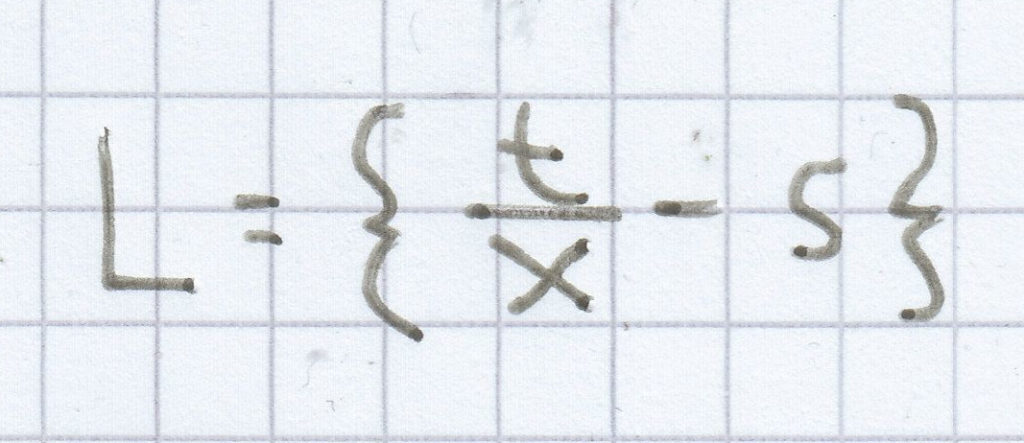
t ist die Lösungsvariable:
rx + sx = t
t = rx + sx
L = {rx + sx}
x ist die Lösungsvariable:
rx + sx = t
x · (r + s) = t | : (r + s)

für r ≠ –s oder: s ≠ –r
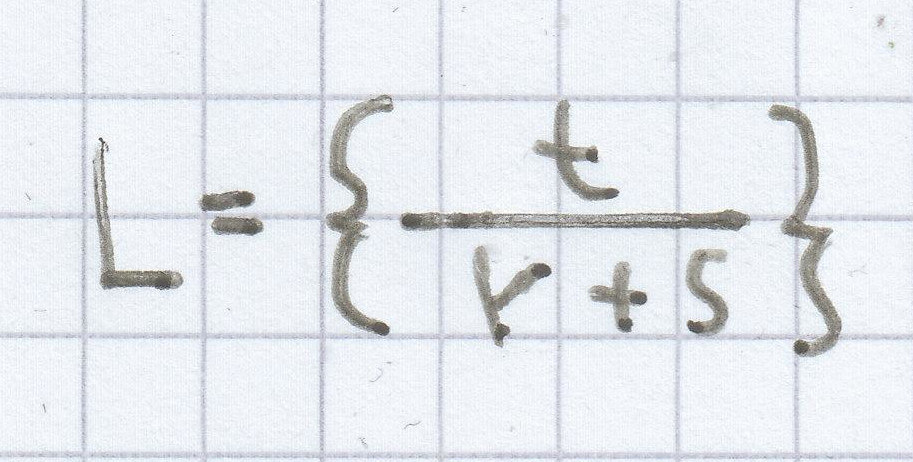
d) r + sx = t
r ist die Lösungsvariable:
r + sx = t | – sx
r = t – sx
L = {t – sx}
t ist die Lösungsvariable:
r + sx = t
t = r + sx
L = {r + sx}
x ist die Lösungsvariable:
r + sx = t | – r
sx = t – r | : s

für s ≠ 0
