
Die wichtigste Regel in Mathe beim Lösen von Ungleichungen ist (das gilt für lineare Ungleichungen und ebenso für alle anderen Ungleichungen): Bei einer Multiplikation mit einer negativen Zahl oder einer Division mit einer negativen Zahl dreht sich bei der Ungleichung das Ungleichheitszeichen um. Das ist superwichtig, es ist schließlich die Kardinalregel bei Ungleichungen. Macht man also z. B. ein „mal (–5)“ / „· (–5)“ so ändert sich beispielsweise das < hin zu >. Macht man hingegen ein „durch (–4)“ / „: (–4)“ so ändert sich ebenso beispielsweise das > hin zu <. Das sollte man bei Ungleichungen so schnell wie möglich verinnerlichen. Wendet man die Kardinalregel bei Ungleichungen nämlich nicht an – so ist auch die spätere Lösungsmenge definitiv falsch. Wenn man aber geschickt umformt, dann kann man sich einen Wechsel des Ungleichheitszeichens ersparen!
Aufgaben zum Mathe-Stoffgebiet: lineare Ungleichungen
1. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Ungleichung.
a) 2x – 3 ≥ –9 + 6x
b) 8y – 1,7 ≥ –40y + 0,3
c) –8,7 – 0,3x ≥ –3,9 + 4x
d) 0,75a + 10 ≤ 8 + 0,5a
2. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der linearen Unlgeichung.
a) 9 – 14 + 8a ≥ 5 – 6a + 4
b) 6y + 2 + 17y > 5 + 23y
c) 12 + 24a – 36a > –19a + 7a + 5
d) –1,3 + 5,6 + 6,6y < –0,5y + 7,1y + 4,3
3. Mathematik-Nachhilfe-Aufgabe: Gib die Lösungsmenge der Ungleichung wieder, die graphisch auf der Zahlengeraden veranschaulicht ist.




4. Mathe-Nachhilfe-Aufgabe: Bestimme jeweils die Lösungsmenge. Was unterscheidet sich hierbei?
a)
–0,4 + 6a + 1,8 ≤ –4a + 2,2 + 10a
–0,4 + 6a + 1,8 > –4a + 2,2 + 10a
b)
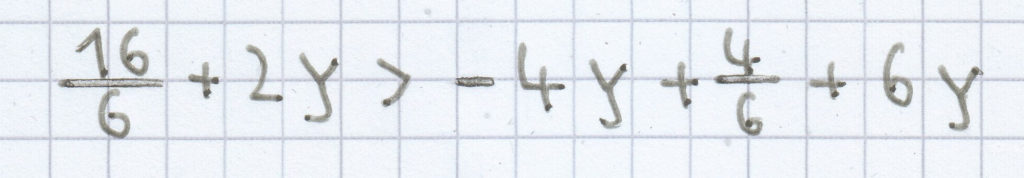
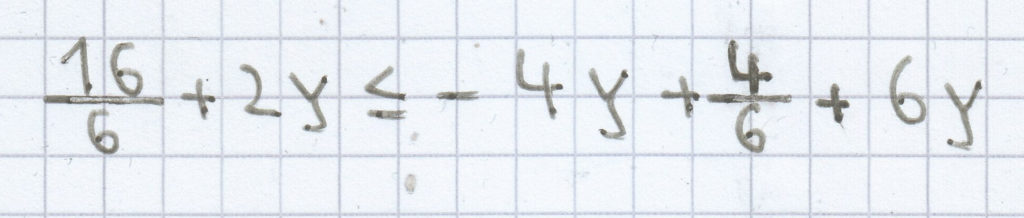
c)
–12 + 36a ≥ –16a + 36 + 4a
–12 + 36a < –16a + 36 + 4a

Lösungen zum Mathematik-Stoffgebiet Lineare Ungleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der Ungleichung.
a)
2x – 3 ≥ –9 + 6x | – 2x
–3 ≥ –9 + 4x | + 9
6 ≥ 4x | : 4
1,5 ≥ x
L = {x | x ≤ 1,5}
b)
8y – 1,7 ≥ –40y + 0,3 | + 40y
48y – 1,7 ≥ 0,3 | + 1,7
48y ≥ 2 | : 48
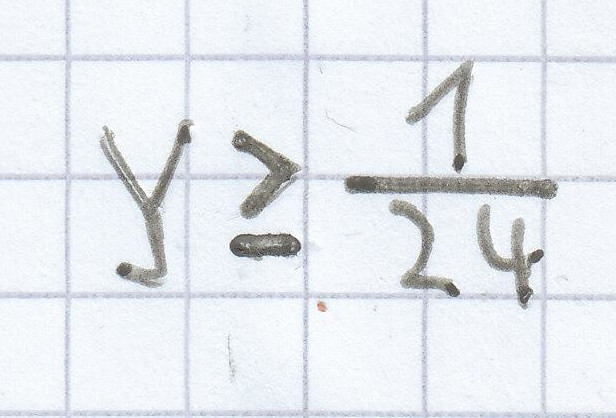
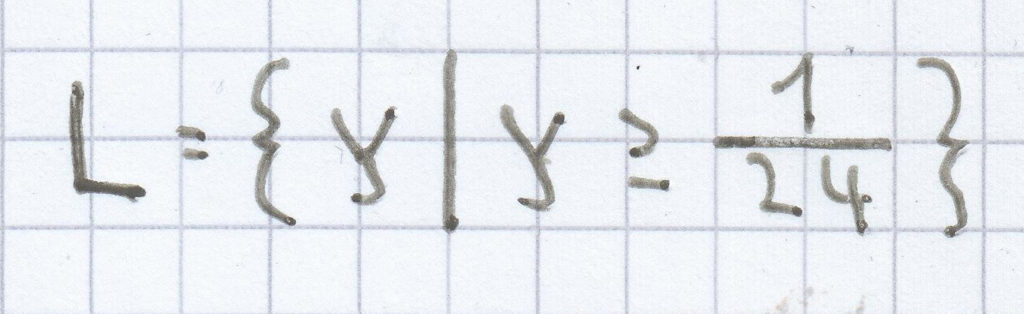
c)
–8,7 – 0,3x ≥ –3,9 + 4x | + 0,3x
–8,7 ≥ –3,9 + 4,3x | + 3,9
–4,8 ≥ 4,3x | : 4,3

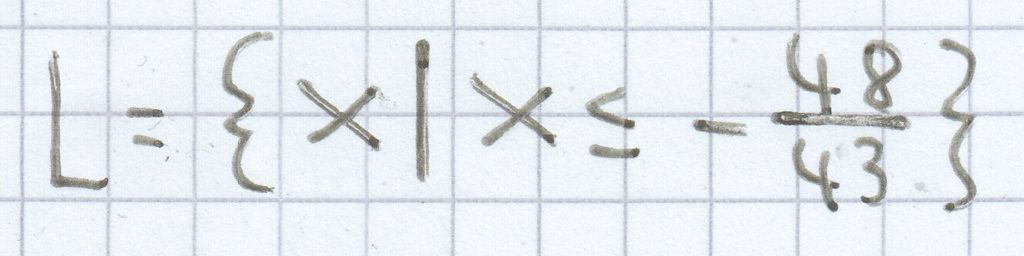
d)
0,75a + 10 ≤ 8 + 0,5a | – 0,5a
0,25a + 10 ≤ 8 | – 10
0,25a ≤ –2 | : 0,25
a ≤ –8
L = {a | a ≤ –8}
2. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der linearen Ungleichung.
a)
9 – 14 + 8a ≥ 5 – 6a + 4
–5 + 8a ≥ 9 – 6a | + 6a
–5 +14a ≥ 9 | + 5
14a ≥ 14 | : 14
a ≥ 1
L = {a | a ≥ 1}
b)
6y + 2 + 17y > 5 + 23y
23y + 2 ≥ 5 + 23y | –23y
2 ≥ 5
L = { } bzw. Ø
c)
12 + 24a – 36a > –19a + 7a + 5
12 – 12a > –12a + 5 | +12a
12 > 5
L = ℚ oder ℝ (je nach Klassenstufe)
d)
–1,3 + 5,6 + 6,6y < –0,5y + 7,1y + 4,3
4,3 + 6,6y < 6,6y + 4,3 | – 6,6y
4,3 < 4,3
L = { } bzw. Ø
3. Mathe-Nachhilfe-Aufgabe: Formuliere die Lösungsmenge, die auf der Zahlengeraden zu sehen ist.

L = {x | x ≥ 3}

L = {x | x ≤ 1}

L = {x | x ≤ –1}

L = {x | x ≥ –4}
4. Mathematik-Nachhilfe-Aufgabe: Gib jeweils die Lösungsmenge an: Was ist hierbei der Unterschied?
a)
–0,4 + 6a + 1,8 ≤ –4a + 2,2 + 10a
–0,4 + 6a + 1,8 > –4a + 2,2 + 10a
–0,4 + 6a + 1,8 ≤ –4a + 2,2 + 10a
1,4 + 6a ≤ 6a + 2,2 | – 6a
1,4 ≤ 2,2 | – 2,2
–0,8 ≤ 0
L = ℚ oder ℝ (je nach Klassenstufe)
–0,4 + 6a + 1,8 > –4a + 2,2 + 10a
1,4 + 6a > 6a + 2,2 | – 6a
1,4 > 2,2 | – 2,2
–0,8 > 0
L = { } bzw. Ø
Wie man hier sehr schön sieht, entscheidet nur das Zeichen der Ungleichung, ob es unendlich viele Lösungen gibt oder keine Lösung.
Man muss sich gerade bei einer speziellen Ungleichung, bei der sich die Variable herauskürzt, immer vor Augen führen, ob die Aussage wahr oder falsch ist – und das am besten, wo man das eindeutig sehen kann, und zwar bei der letzten mittels Äquivalenzumformungen erhaltenen Ungleichung.
b)
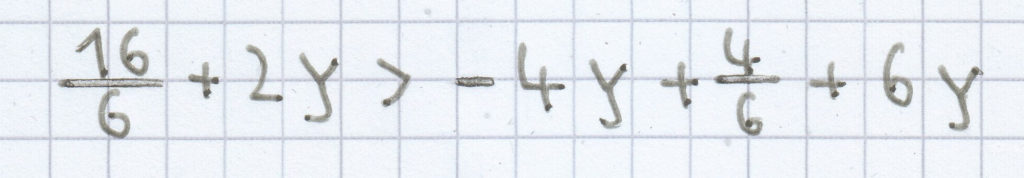
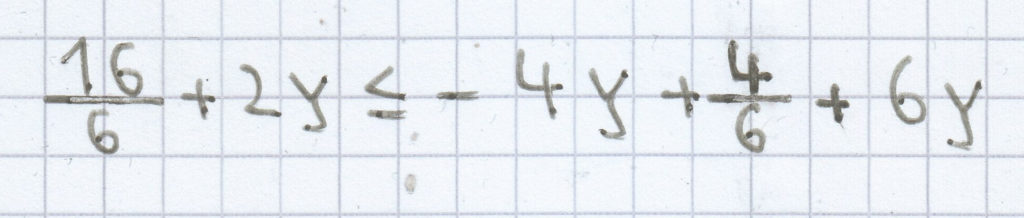
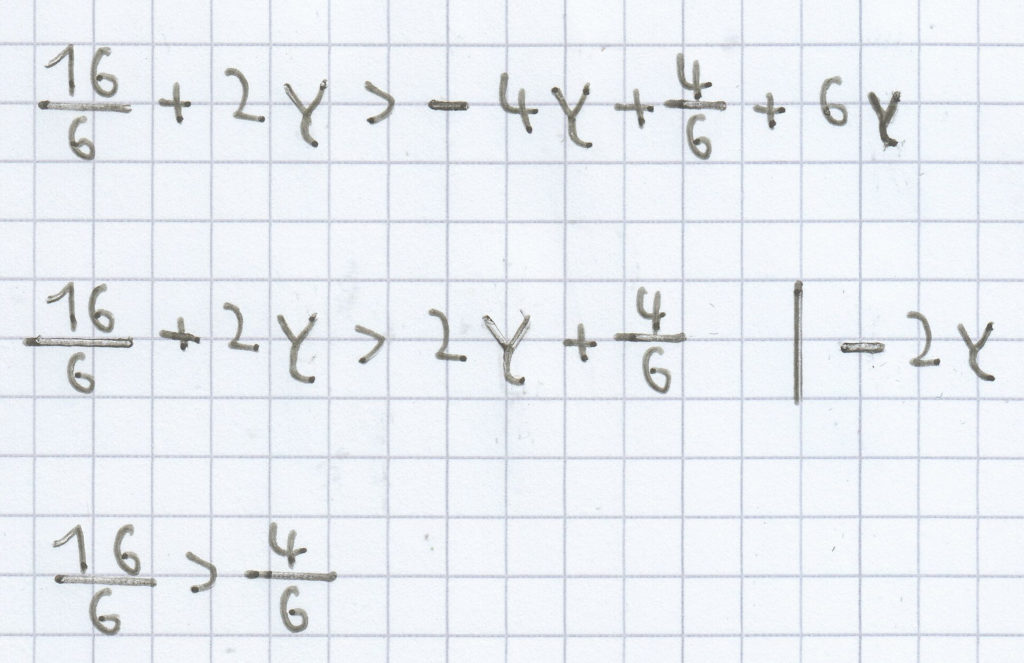
L = ℚ oder ℝ (je nach Klassenstufe)
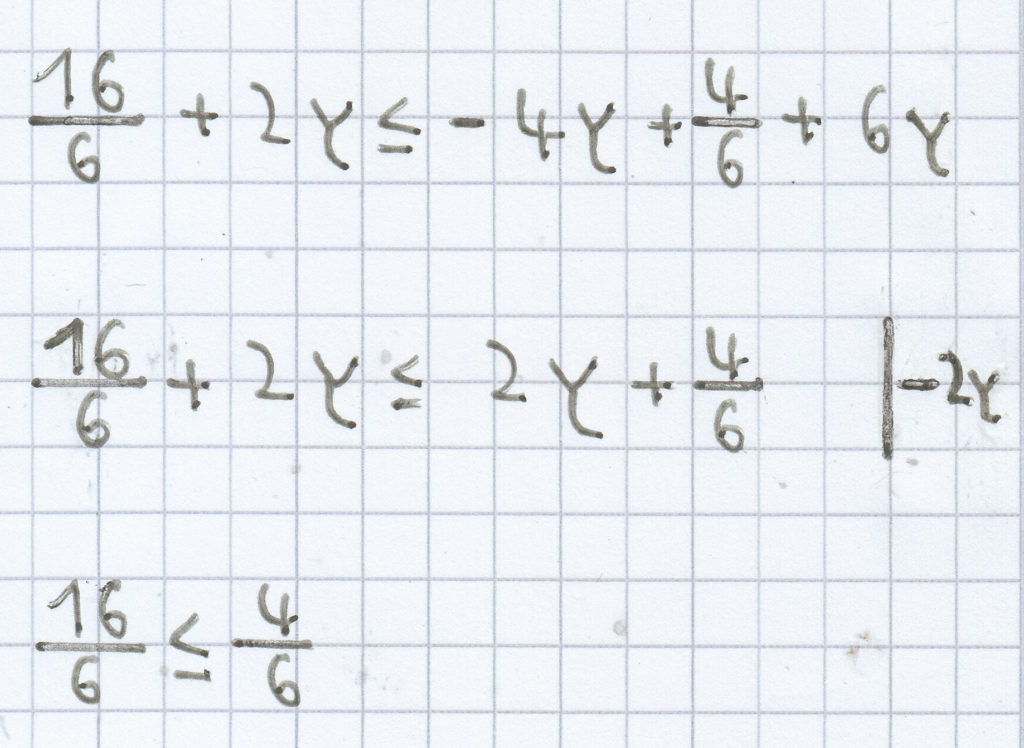
L = { } bzw. Ø
c)
–12 + 36a ≥ –16a + 36 + 4a
–12 + 36a < –16a + 36 + 4a
–12 + 36a ≥ –16a + 36 + 4a
–12 + 36a ≥ –12a + 36 | + 12a
–12 +48a ≥ 36 | + 12
48a ≥ 48 | : 48
a ≥ 1
L = {a | a ≥ 1}
–12 + 36a < –16a + 36 + 4a
–12 + 36a < –12a + 36 | + 12a
–12 + 48a < 36 | + 12
48a < 48 | : 48
a < 1
L = {a | a < 1}