Beim Flächeninhalt von Vielecken im Fach Mathematik muss man entweder die Fläche exakt mittels Formel berechnen oder zeichnerisch ermitteln, bei dem wiederum auch eine Rechnung gemacht werden muss. Die zwei Verfahren zum Bestimmen des Flächeninhaltes unterscheiden sich hierbei in ihrer Exaktheit. Die rechnerische Methode ist immer ganz, ganz exakt, die zeichnerische nicht. Interessant hierbei ist aber, dass das zeichnerische Ermitteln des Flächeninhalts realitätskonform ist, sprich ein Abbild der Realität ist, der rechnerische Weg hingegen nicht. Kein Flächeninhalt, den man rein rechnerisch bestimmt, kommt so in der Realität auch 100 % identisch auch so vor. Alle Flächen, die man sieht, sei es Rechtecke, Parallelogramme, Trapeze oder andere Vielecke verlaufen nämlich nicht exakt so wie man sie am Computer (!) zeichnen kann!
Aufgaben zum Mathematik-Stoffgebiet: der Flächeninhalt von Vielecken
1. Mathematik-Nachhilfe-Aufgabe: Welcher Sportplatz ist größer? Sportplatz 1 ist 88 Meter lang und 67 Meter breit, Sportplatz 2 ist 84 Meter lang und 69 Meter breit.
2. Mathe-Nachhilfe-Aufgabe: Zeichne das Parallelogramm ABCD in ein Koordinatensystem (1 cm = 1 Längeneinheit). Ermittle darauf den Flächeninhalt des Parallelogramms, ohne Messen einzelner Längen.
A (4 | 8)
B (11 | 8)
C (12 | 10)
D (5 | 10)
3. Mathematik-Nachhilfe-Aufgabe: Zeichne ein Dreieck ABC und ermittle durch Messen dessen Flächeninhalt und Umfang.
a = 4,2 cm; β = 42°; γ = 48°
4. Mathe-Nachhilfe-Aufgabe: Es ist folgendes Trapez gegeben. Das gleiche Trapez soll auf Karopapier übertragen werden und die Längen abgemessen werden. Anschließend soll dessen Flächeninhalt berechnet werden, indem man die hierzu notwendigen Längen abmisst.

Lösungen zum Mathematik-Stoffgebiet: der Flächeninhalt von Vielecken
1. Mathe-Nachhilfe-Aufgabe: Es soll berechnet werden, welcher Fußballplatz größer ist. Der erste Sportplatz ist 88 Meter lang und 67 Meter breit, der zweite Sportplatz ist 84 Meter lang und 69 Meter breit.
Bei einem Fußballplatz liegt immer ein rechteckige Fläche vor, sprich ein Rechteck.
AR = a · b
Der 1. Fußballplatz hat folgende Fläche:
A1 = 88 m · 67 m
A1 = 5896 m²
Der 2. Fußballplatz hat diese Fläche:
A2 = 84 m · 69 m
A2 = 5796 m²
Der erste Fußballplatz hat die größte Fläche.

2. Mathematik-Nachhilfe-Aufgabe: Es soll ein Parallelogramm ABCD gezeichnet werden (1 cm = 1 Längeneinheit). Anschließend soll der Flächeninhalt berechnet werden, ohne hierbei die Längen des Parallelogramm abzumessen.
A (4 | 8)
B (11 | 8)
C (12 | 10)
D (5 | 10)
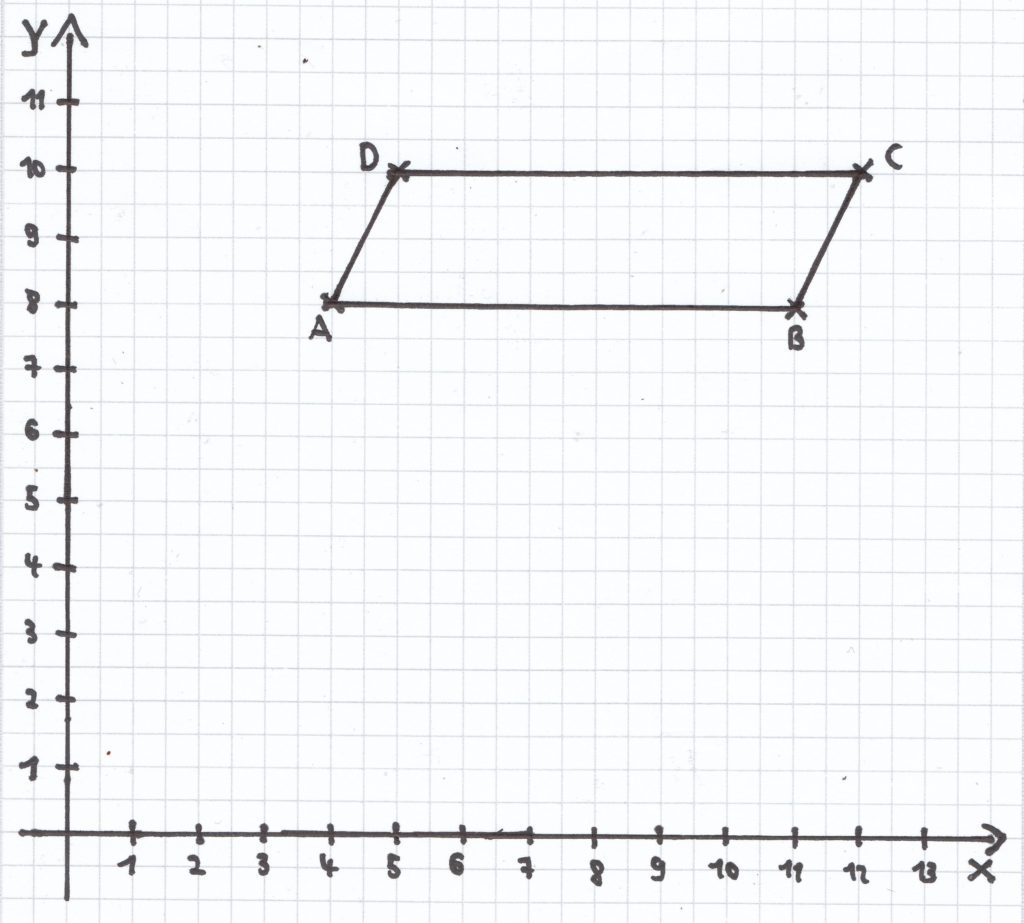
Den Flächeninhalt eines Parallelogramms kann man folgendermaßen berechnen:
AP = g · h
Die Länge der Grundseite ergibt sich hier in der Aufgabe auf diese Weise, indem man die beiden x-Koordinaten der Punkte B und A voneinander abzieht (natürlich kann man aber auch die Punkte C und D voneinander abziehen).
g = BX – AX
g = 11 cm – 4 cm
g = 7 cm
Die Höhe des Parallelogramm in Abhängigkeit zur Grundseite kann man einfach berechnen, wenn man beispielsweise die y-Koordinate von den Punkten Punkten D und A voneinander abzieht oder von den Punkten C und B.
h = Dy – Ay
h = 10 cm – 8 cm
h = 2 cm
Darauf kann man den Flächeninhalt des Parallelogramms berechnen.
AP = g · h
AP = 7 cm · 2 cm
AP = 14 cm²
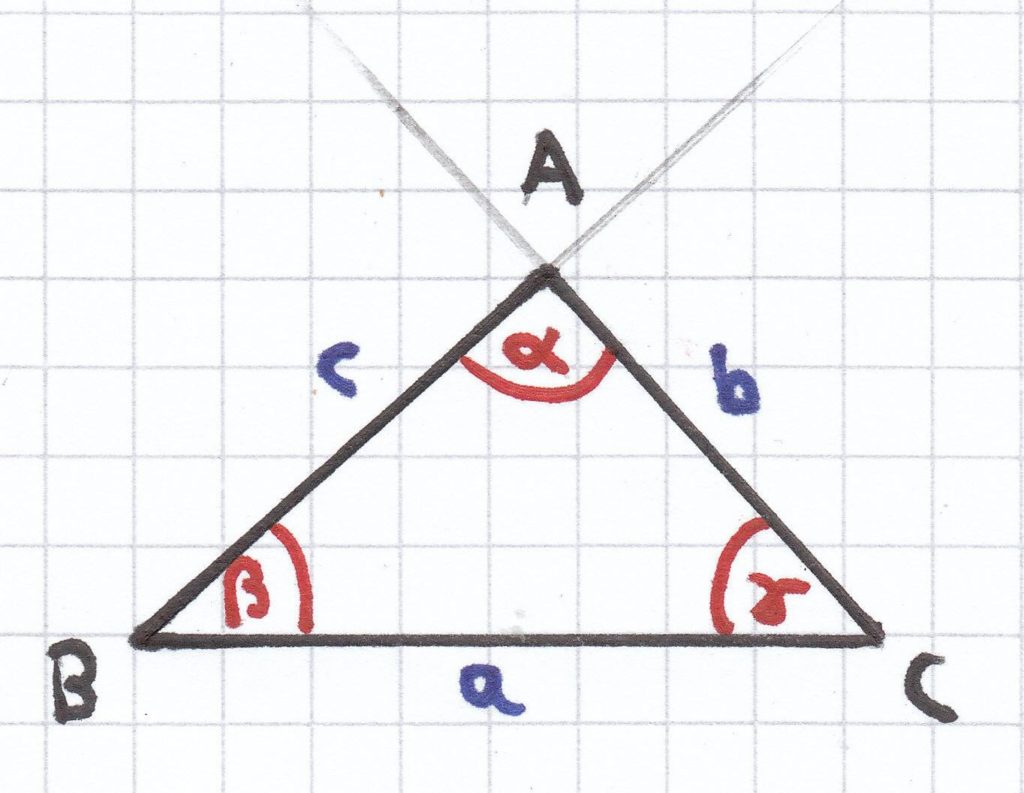
3. Mathe-Nachhilfe-Aufgabe: Es soll ein bestimmtes Dreieck gezeichnet werden und anschließend durch Messen dessen Flächeninhalt und Umfang bestimmt werden.
a = 4,2 cm; β = 42°; γ = 48°
Das Dreieck zeichnet man am besten so in ein kariertes Papier, dass die Seite a entlang der Karos verläuft. Dadurch ergibt sich der Punkt B und der Punkt C des Dreiecks. An die Punkte legt man dann schließlich die beiden gegebenen Winkel β und γ an und zieht jeweils eine Linie. Der Schnittpunkt beider Linien ergibt den Punkt A des Dreiecks.
Von der Seite a ausgehend, kann man durch Messen die Höhe ha bestimmen. Die Höhe ha verläuft hierbei rechtwinklig zur Grundseite a durch den Punkt A. Durch Messen ergibt sich ungefähr folgende Länge:
ha = 2,1 cm
Beim Messen erhält man oft Dezimalzahlen. Deshalb ist es wichtig, dass man zuerst sehr genau zeichnet und dann sehr genau das Ergebnis vom Geodreieck abliest. Hierbei gilt als Faustformel, dass die Abweichung vom tatsächlichen Ergebnis maximal ± 0,1 mm sein sollte.
Allgemein gilt ja für die Berechnung des Flächeninhalts eines Dreiecks:
AD = 0,5 · g · h
Auf dieses Dreieck bezogen gilt:
AD = 0,5 · a · ha
AD = 0,5 · 4,2 cm · 2,1 cm
AD = 4,41 cm²
Allgemein berechnet man den Umfang eines Dreiecks wie folgt:
UD = a + b + c
Durch Messen ergibt sich für die Seite b ungefähr:
b = 2,8 cm
Und für die Seite c ergibt sich durch Messen ungefähr folgende Länge:
c = 3,1 cm
Darauf kann man nun den Umfang des Dreiecks berechnen:
UD = 4,2 cm + 2,8 cm + 3,1 cm
UD = 10,1 cm
4. Mathematik-Nachhilfe-Aufgabe: Nachfolgendes Trapez soll auf ein Karopapier übertragen werden. Hierbei sollen die Längen abgemessen werden. Daraufhin soll dessen Flächeninhalt berechnet werden, indem man die hierzu notwendigen Längen abmisst.

Durch Messen erhält man gegen den Uhrzeigesinn und von der unteren waagrechten Seite beginnend, ungefähr folgende Maße:
a = 6,5 cm
b = 3,3 cm
c = 3,5 cm
d = 2,7 cm
Für die Berechnung des Flächeninhalts eines Trapezes benötigt nun man deren Höhe. Durch Messen ergibt sich hier:
h = 2,5 cm
Der Flächeninhalt eines Trapezes berechnet sich wie folgt:
AT = 0,5 · (a + c) · h
Auf dieses Beispiel bezogen ergibt sich daher folgender Flächeninhalt:
AT = 0,5 · (6,5 cm + 3,5 cm) · 2,5 cm
AT = 0,5 · 10 cm · 2,5 cm
AT = 12,5 cm²