
Neben Gleichungen gibt es in Mathematik noch sogenannte Ungleichungen. Wie der Name es schon vermuten lässt, unterscheiden sich hierbei Ungleichungen offenbar fundamental von Gleichungen, da die Vorsilbe „un“ im Deutschen immer eine Negation ausdrückt – und das demzufolge hier auch der Fall ist. Daher sind Ungleichungen definitiv keine Gleichungen – aber auch nicht komplett das Gegenteil davon.
Der zentrale Unterschied ist im Prinzip das Zeichen, das bei Ungleichungen auftritt. Denn bei einer Ungleichung wird normalerweise entweder ein „>“/„größer als“ oder ein „<“/„kleiner als“ verwendet anstatt wie bei einer Gleichung ein „=“/„gleich“. Dadurch gibt es auch im Gegensatz zu einer Gleichung niemals als Lösungsmenge eine einzige Lösung.
Bei der Ermittlung der Lösungsmenge gibt es aber eine signifikante Übereinstimmung zu Gleichungen. Sowohl Gleichungen als auch Ungleichungen löst man nämlich primär über Äquivalenzumformungen. Weiß man daher wie Äquivalenzumformungen in Mathe richtig gemacht werden, so kann man im Prinzip auch schon Ungleichungen lösen. Das ist doch super, so ökonomisch für die grauen Zellen kann nämlich Mathe auch sein!

Tritt bei einer Ungleichung übrigens ein „≥“/„größer gleich“ oder ein „≤“/„kleiner gleich“ auf, dann sind zwar die primären Zeichen einer Gleichung und einer Ungleichung kombiniert, eine einzige Lösung als Lösungsmenge tritt hier dann aber trotzdem ebenfalls niemals auf.
Aufgaben zum Mathematik-Stoffgebiet: Ungleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der Ungleichungen.
a) 7x + 8 > 2x – 5
b) –5x + 3 > –17
c) x –19x > 90
d) 9x + 4x > 5x – 1
e) 2x – 8x < –42
f) –8 – 0,2x < 1
g) –3x + 0,6 < –2,4 + 3x
h)
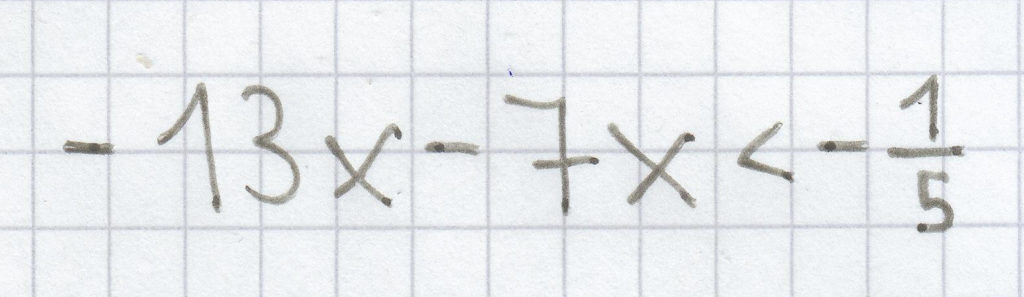
i)
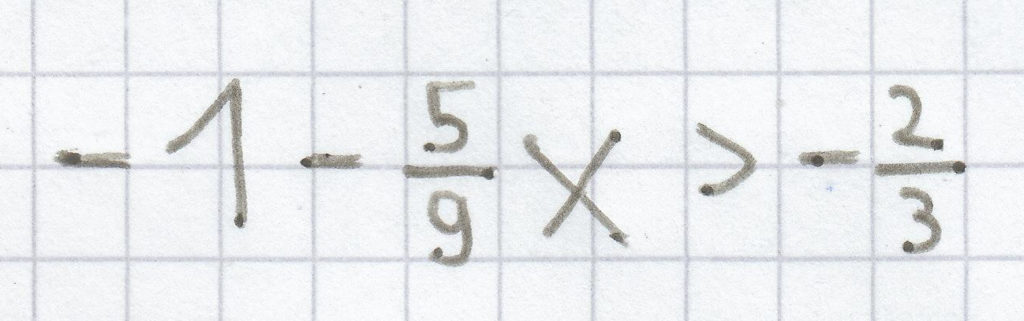
j)
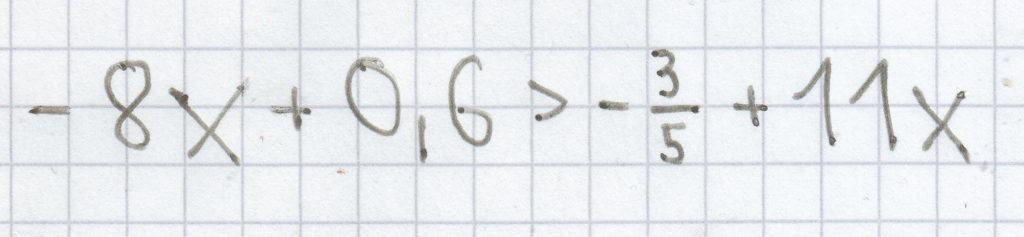
2. Mathe-Nachhilfe-Aufgabe: Welche Aussagen sind hier wahr, welche falsch?
a)
9 ≥ 4
7 ≥ 7
–7 ≥ –2
b)
4 ≤ 9
–5 ≤ –5
8 ≤ –1
c)
0,58 ≤ 0,33
31,6 ≤ 31,7
–43 ≤ –4,3
d)
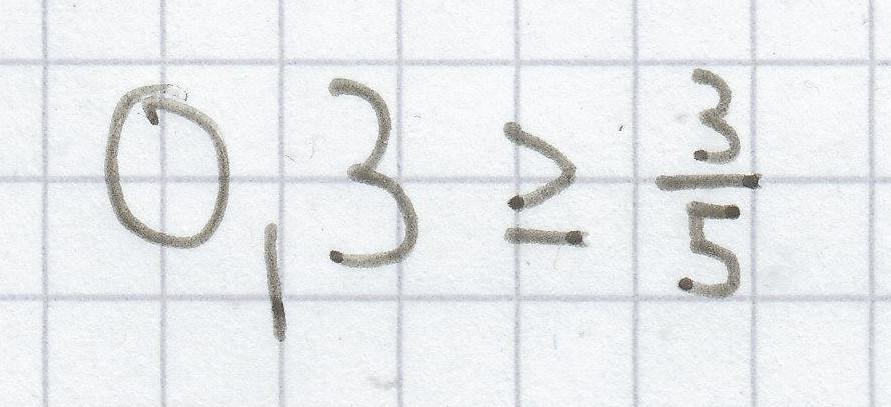
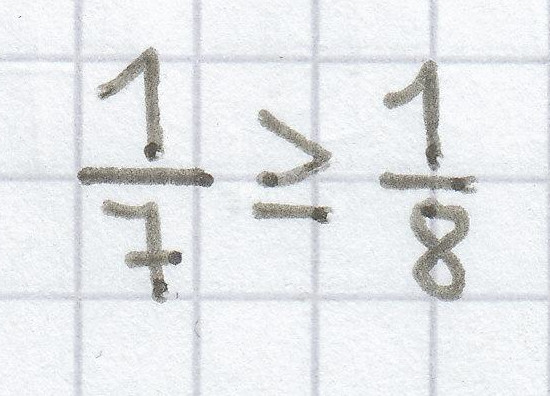
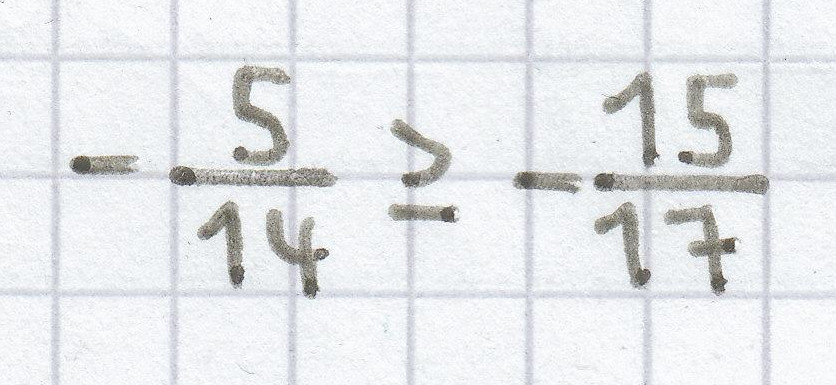
3. Mathematik-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge.
a) 73 + x ≤ 76
b) 3,5 + x ≤ 0
c) –30 + x ≥ –20
d) 4x – 3 + 12x ≥ 0
e) 8x ≥ x + 24
f) 10 ≤ –2x – 35
4. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Ungleichung.
a) x + 99 > –14x + 24
b) 4x + 18x – 13 < 20x
c) –3,5 + 10x < –28,7 + 3x
d) –0,2x + 0,4 > –1,3x + 8,1
e) –24y + 30y – 12 > –70 + 5y
f) 5a + 8a + 0,3 < –0,8 + 7a + 1,1
g)
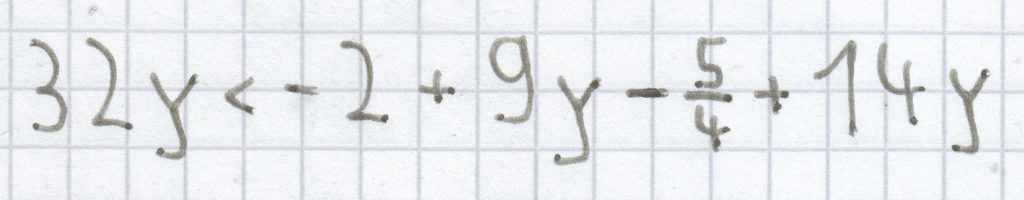
h) 25 + 12t > –9t + 33 + 17t

Lösungen zu dem Mathematik-Stoffgebiet Ungleichungen
1. Mathe-Nachhilfe-Aufgabe: Bestimme bei den Ungleichungen die Lösungsmenge.
a)
7x + 8 > 2x – 5 | – 2x <=>
5x + 8 > –5 | – 8
5x > –13 | : 5
x > –2,6
L = {x | x > –2,6}
b)
–5x + 3 > –17 | – 3
–5x > –20 | : (–5)
x < 4
L = {x | x < 4}
c)
x –19x > 90 <=>
–18x > 90 | : (–18)
x < –5
L = {x | x < –5}
d)
9x + 4x > 5x – 1 <=>
13x > 5x – 1 | – 5x
8x > –1 | : 8
x > –0,125
L = {x | x > –0,125}
e)
2x – 8x < –42 <=>
–6x < –42 | : (–6)
x > 7
L = {x | x > 7}
f)
–8 – 0,2x < 1 | + 8 <=>
–0,2x < 9 | : (–0,2)
x > –45
L = {x | x > –45}
g)
–3x + 0,6 < –2,4 + 3x | – 3x <=>
–6x + 0,6 < –2,4 | – 0,6
–6x < –3 | : (–6)
x > 0,5
L = {x | x > 0,5}
h)
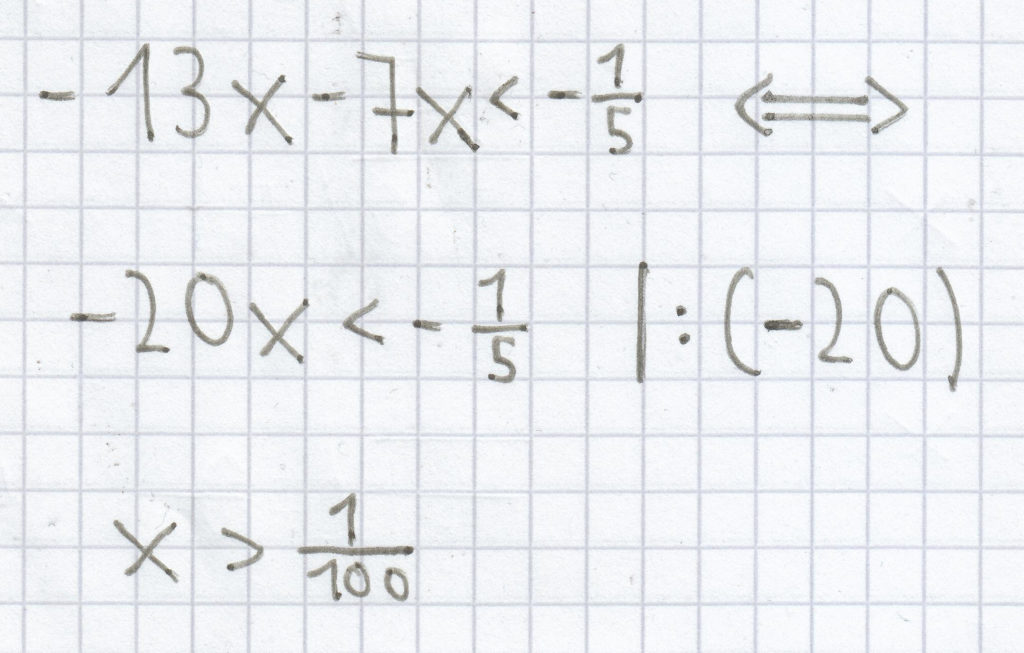
L =
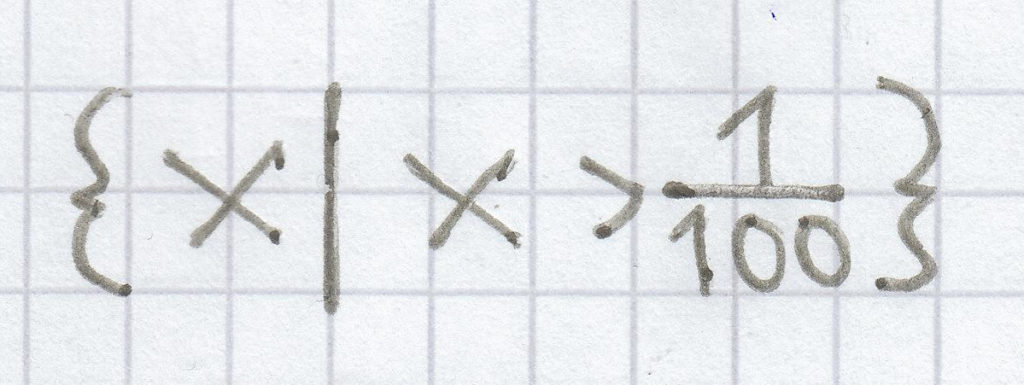
i)
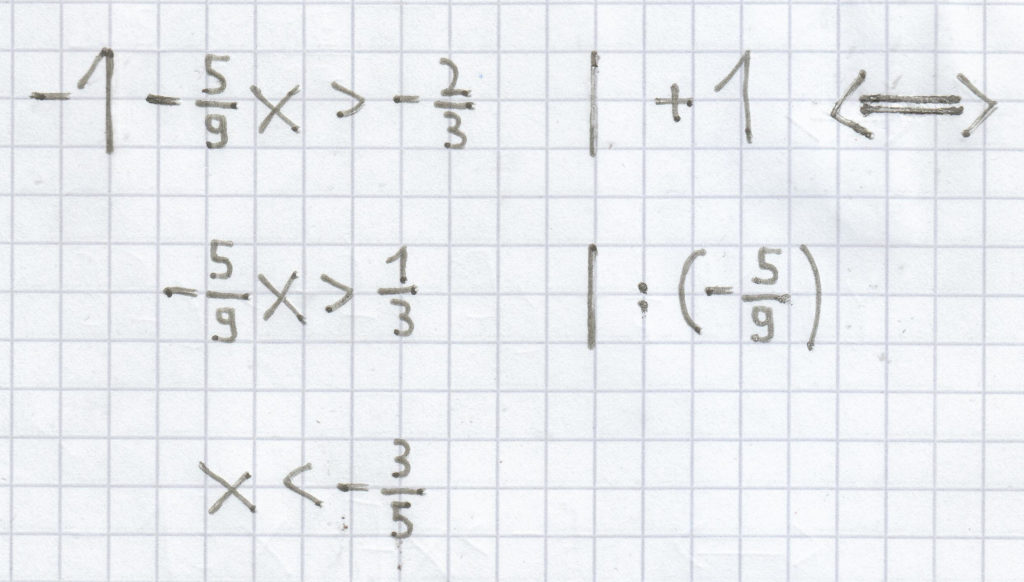
L =
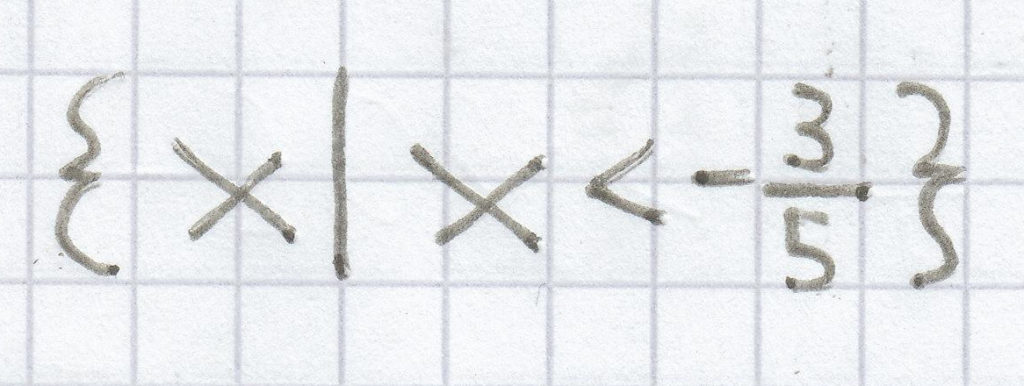
j)
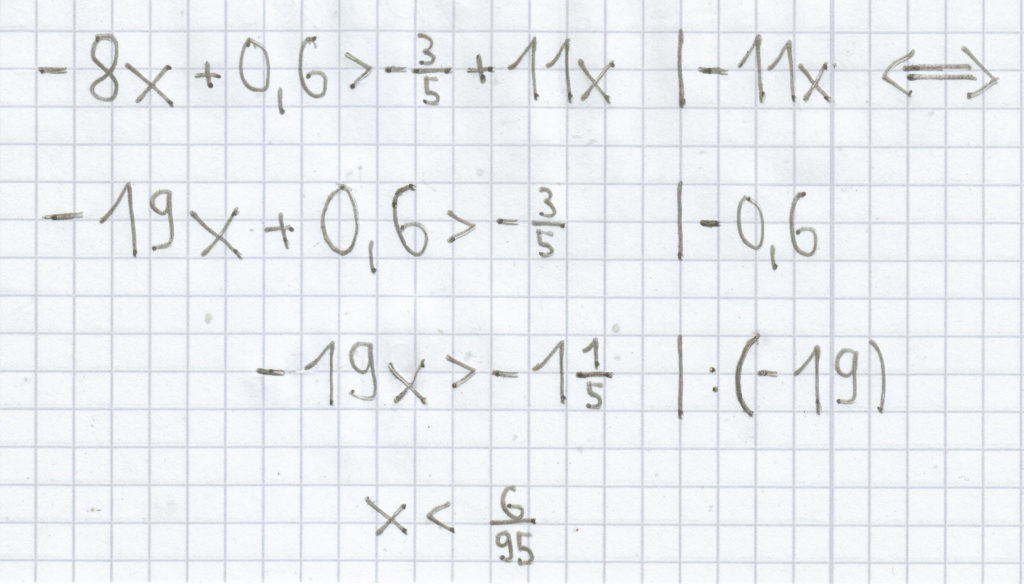
L =
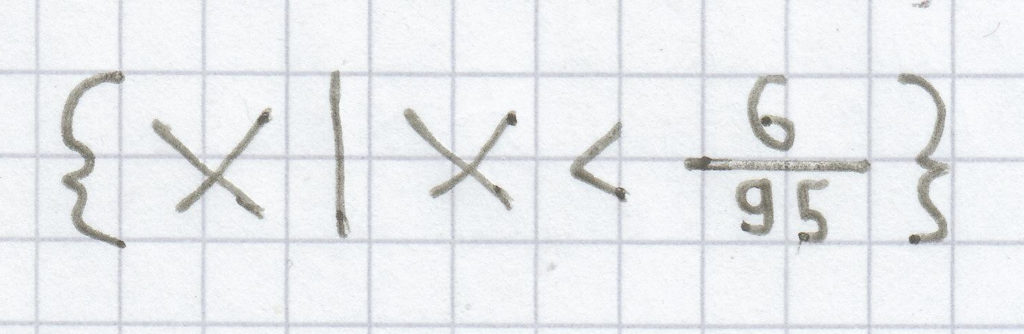
2. Mathematik-Nachhilfe-Aufgabe: Ist die Aussage der Ungleichung wahr oder falsch?
a) 9 ≥ 4
Hier liegt eine wahre Aussage vor, da 9 immer „größer gleich“ 4 ist.
a) 7 ≥ 7
Hier liegt ebenfalls eine wahre Aussage vor, da 7 immer „größer gleich“ 7 ist.
a) –7 ≥ –2
Hier liegt eine unwahre Aussage vor, da –7 niemals „größer gleich“ –2 ist.
b) 4 ≤ 9
Die Ungleichung ist immer wahr, da 4 immer „kleiner gleich“ 9 ist.
b) –5 ≤ –5
Auch diese Ungleichung ist immer wahr, das –5 immer „kleiner gleich“ –5 ist.
b) 8 ≤ –1
Die Gleichung ist immer unwahr, da 8 niemals „kleiner gleich“ –1 ist.
c) 0,58 ≤ 0,33
Die Ungleichung ist niemals wahr da 0,58 niemals „kleiner gleich“ 0,33 ist.
c) 31,6 ≤ 31,7
Hier liegt eine wahre Aussage vor, da 31,6 immer „kleiner gleich“ 31,7 ist.
c) –43 ≤ –4,3
Die Ungleichung ist immer wahr, da –43 immer „kleiner gleich“ –4,3 ist.
d)
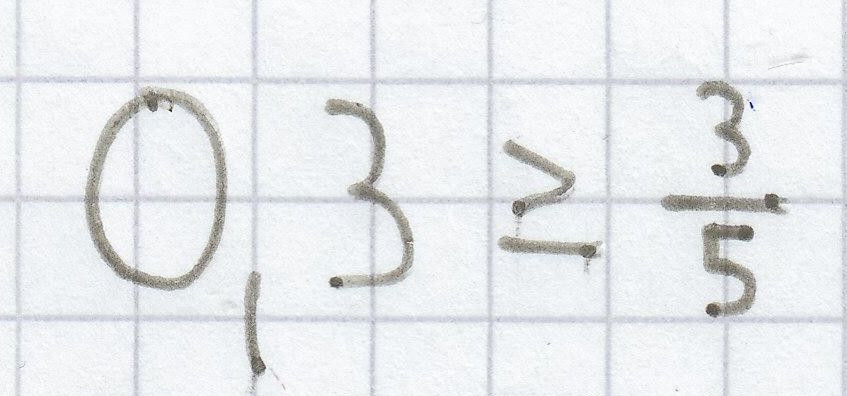
Die Ungleichung ist immer unwahr, da 0,3 niemals „größer gleich“

ist.
d)
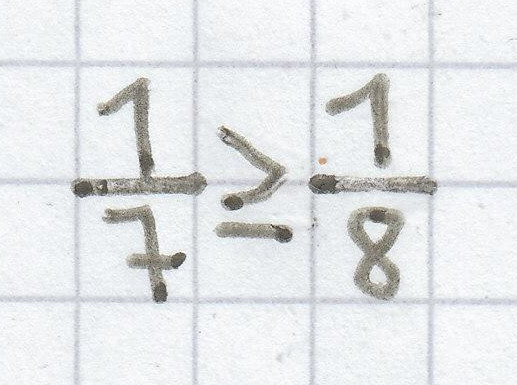
Hier liegt eine wahre Aussage vor, da
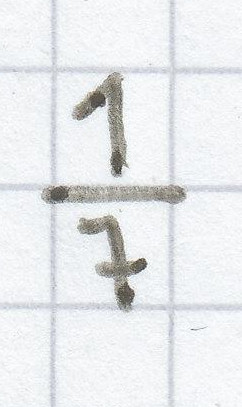
immer „größer gleich“
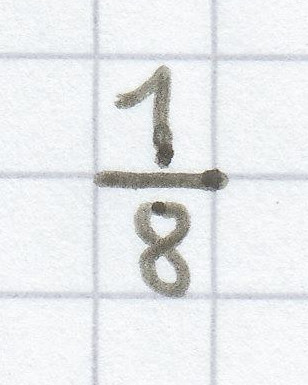
ist.
d)
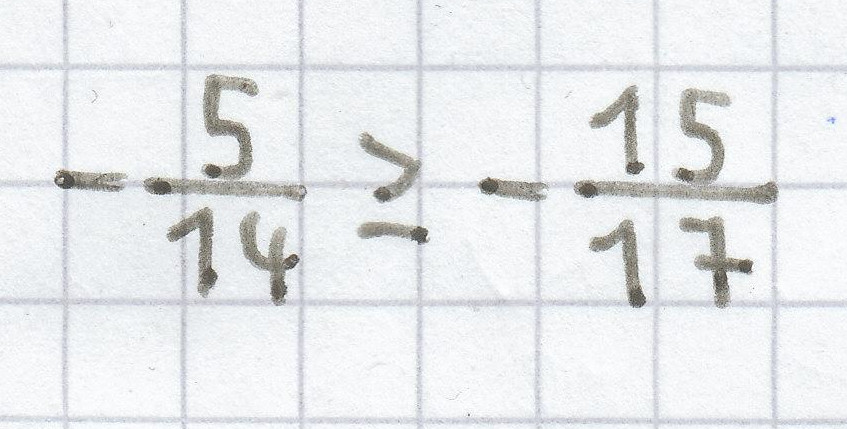
Die Ungleichung ist immer wahr, da
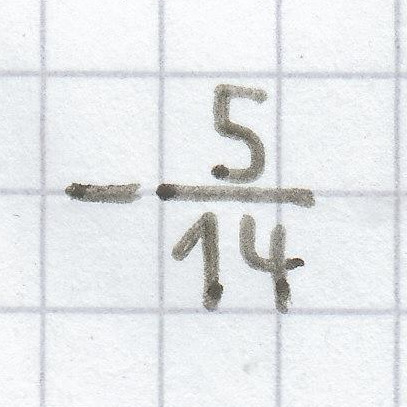
≥ immer „größer gleich“
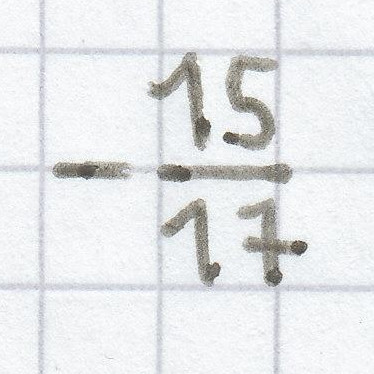
ist.
3. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der Ungleichung.
a)
73 + x ≤ 76 | – 73 <=>
x ≤ 3
L = {x | x ≤ 3}
b)
3,5 + x ≤ 0 | – 3,5 <=>
x ≤ –3,5
L = {x | x ≤ –3,5}
c)
–30 + x ≥ –20 | + 30 <=>
x ≥ 10
L = {x | x ≥ 10}
d)
4x – 3 + 12x ≥ 0 <=>
16x – 3 ≥ 0 | + 3
16x ≥ 3 | : 16
x ≥ 0,1875
L = {x | x ≥ 0,1875}
e)
8x ≥ x + 24 | – x <=>
7x ≥ 24 | : 7
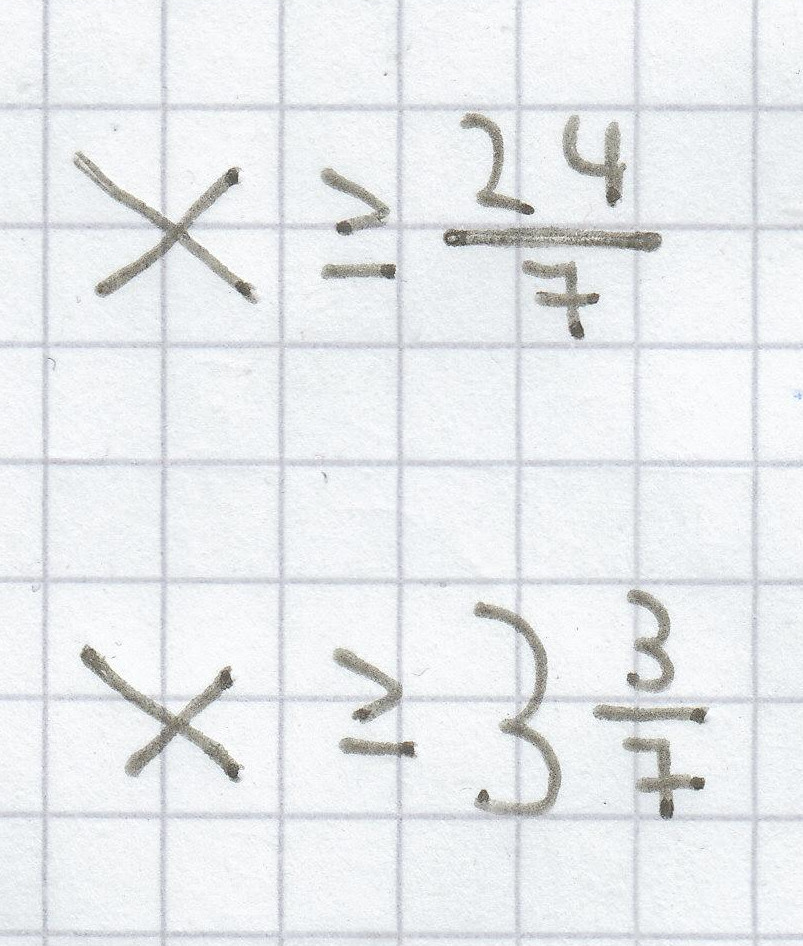
L =
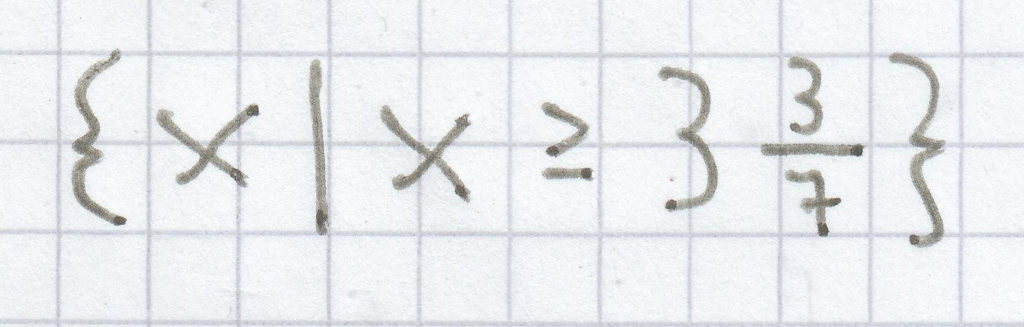
f)
10 ≤ –2x – 35 | + 35 <=>
45 ≤ –2x | : (–2)
x ≥ –22,5
L = {x | x ≥ –22,5}
4. Mathematik-Nachhilfe-Aufgabe: Welche Lösungsmenge weist die Ungleichung auf?
a)
x + 99 > –14x + 24 | + 14x <=>
15x +99 > 24 | – 99
15x > –75 | : 15
x > –5
L = {x | x > –5}
b)
4x + 18x – 13 < 20x <=>
22x – 13 < 20x | – 22x
–13 < –2x | : (–2)
x > 6,5
L = {x | x > 6,5}
c)
–3,5 + 10x < –28,7 + 3x | – 3x <=>
–3,5 + 7x < –28,7 | + 3,5
7x < 25,2 | : 7
x < –3,6
L = {x | x < –3,6}
d)
–0,2x + 0,4 > –1,3x + 8,1 | + 1,3x <=>
1,1x + 0,4 > 8,1 | – 0,4
1,1x > 7,7 | : 1,1
x > 7
L = {x | x > 7}
e)
–24y + 30y – 12 > –70 + 5y <=>
6y – 12 > –70 + 5y | – 5y
y – 12 > –70 | + 12
y > –58
L = {y | y > –58}
f)
5a + 8a + 0,3 < –0,8 + 7a + 1,1 <=>
13a + 0,3 < 0,3 + 7a | – 7a
6a + 0,3 < 0,3 | – 0,3
6a < 0 | : 6
a < 0
L = {a | a < 0}
g)
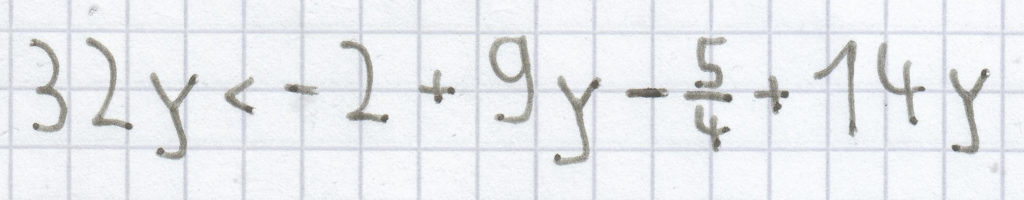
32y < –3,25 + 23y | – 23 <=>
9y < –3,25 | : 9
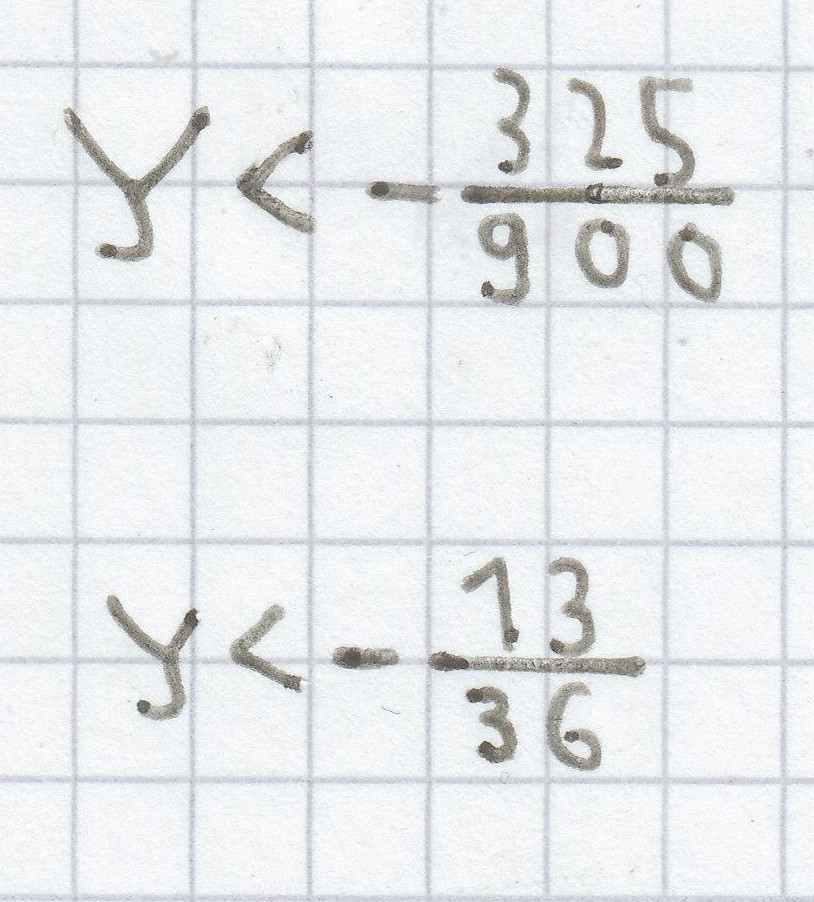
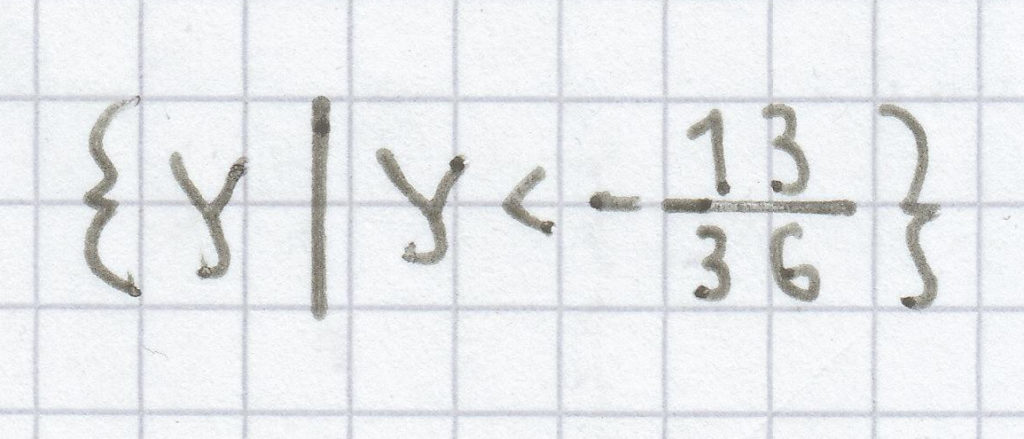
h)
25 + 12t > –9t + 33 + 17t <=>
25 + 12t > 33 + 8t | – 8t
25 + 4t > 33 | – 25
4t > 8 | : 4
t > 2
L = {t | t > 2}