1. Allgemeines zu Vierecken
Eine der wichtigsten geometrischen Figuren in Mathe stellen Vierecke dar. Anhand von verschiedenen besonderen Vierecken, wie beispielsweise Rechteck, Quadrat, Parallelogramm, können im Fach Mathematik nämlich vielfache „Viereckuntersuchungen“ gemacht werden. Gerade besondere Vierecke weisen ja ganz viele Gesetzmäßigkeiten auf. Alle Berechnungen und zeichnerischen Darstellungen hierzu basieren darauf.
Definition eines Vierecks:
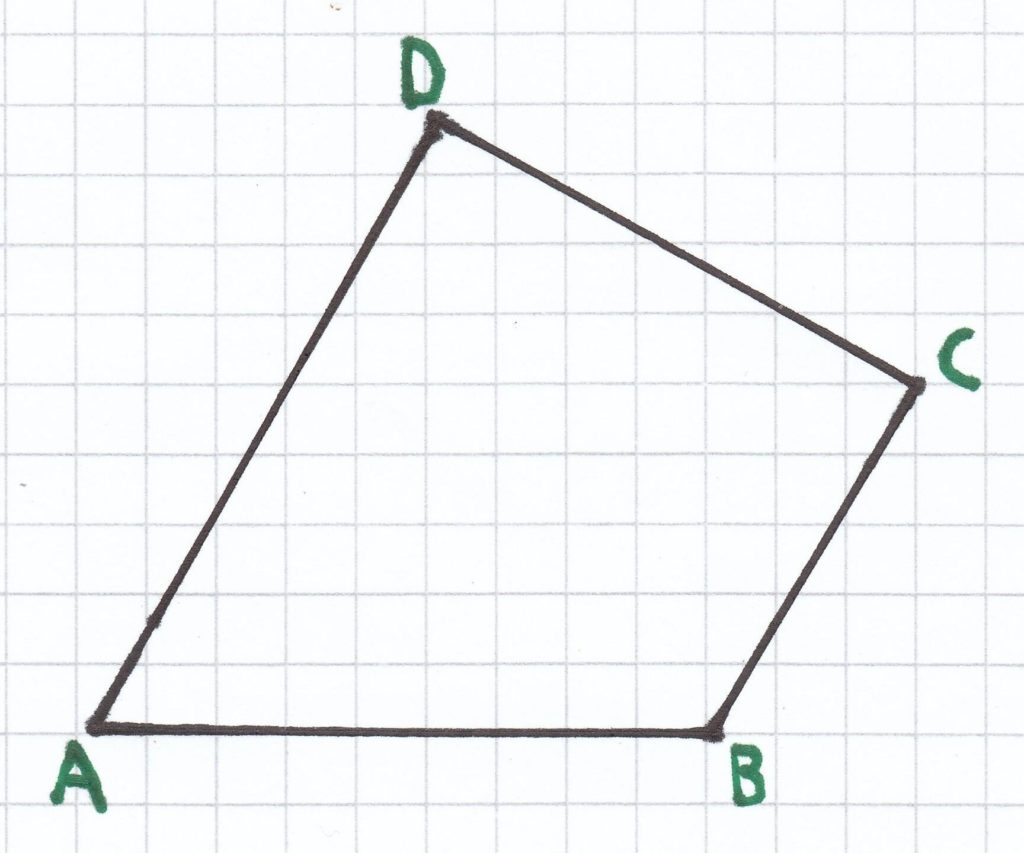
1. Ein Viereck stellt immer eine Fläche dar. Jedes Viereck besteht hierbei aus vier Punkten. Diese werden die Eckpunkte des Vierecks genannt. Drei Eckpunkte dürfen hierbei nicht auf einer Geraden liegen, auch dürfen sich die Seiten nicht überschneiden.
2. Jede Verbindungsstrecke zweier Eckpunkte, die miteinander keine Seite bilden, nennt man Diagonale des Vierecks.
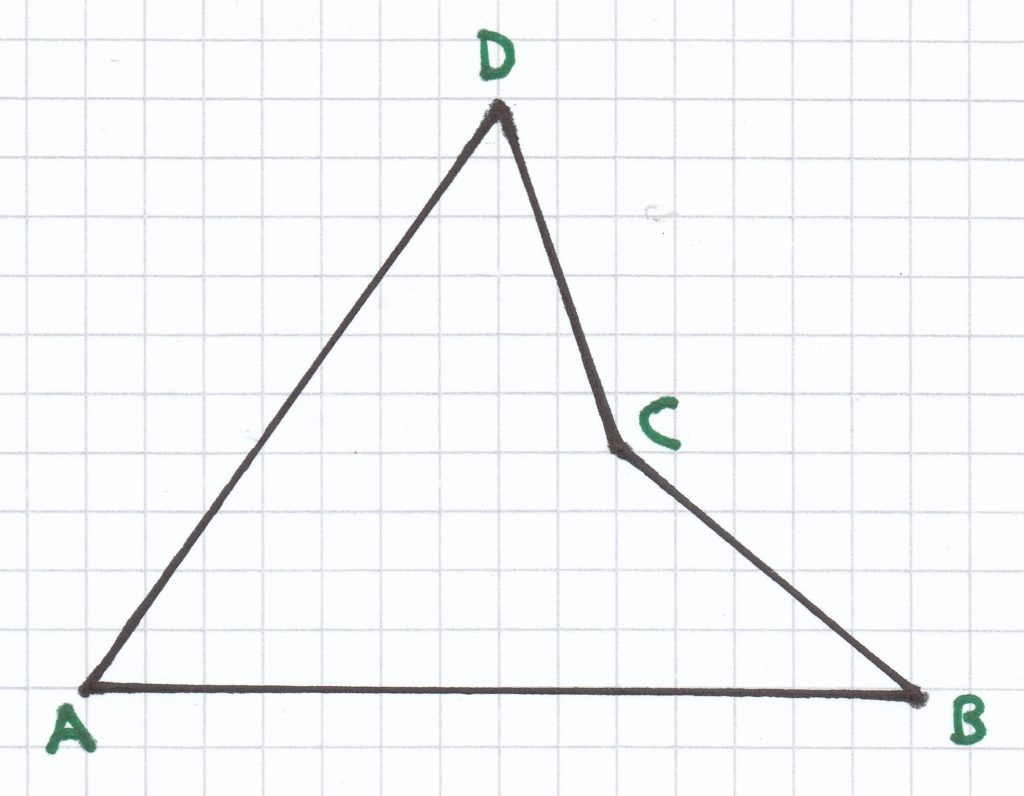
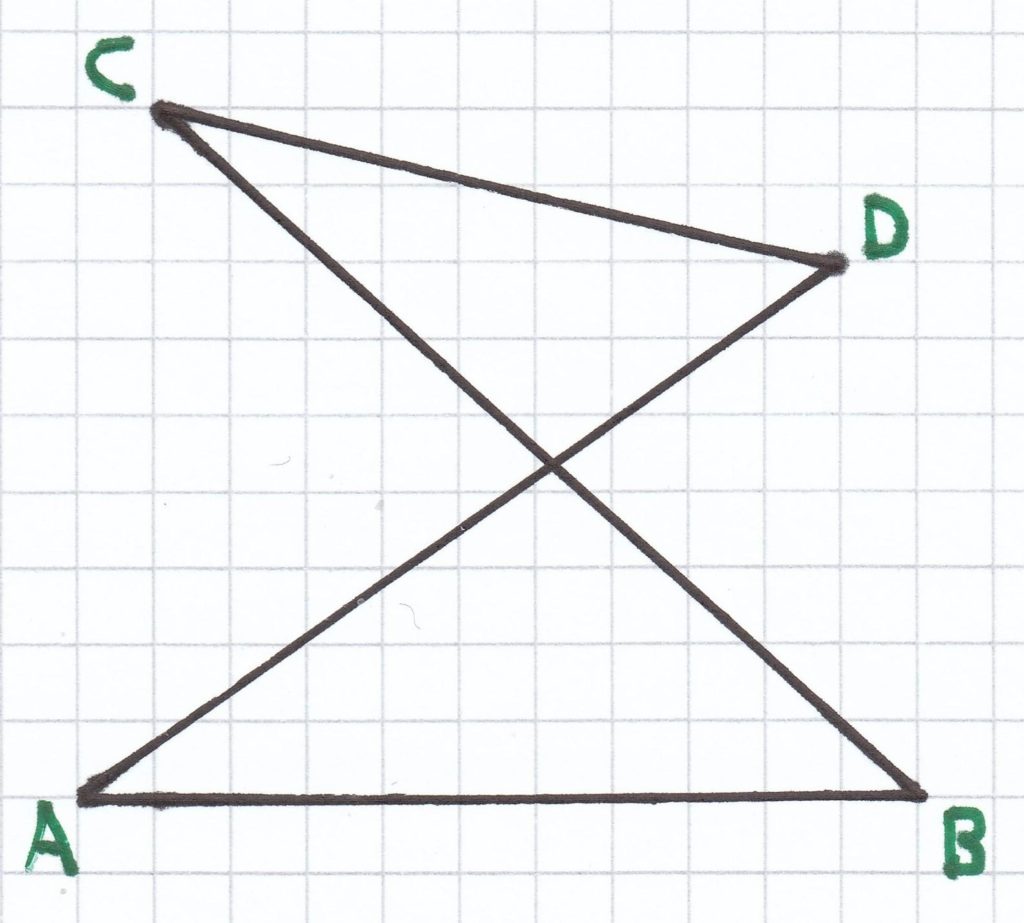
Liegen drei Eckpunkte auf einer Geraden, so kann man logischerweise keine vier Eckpunkte mehr bilden – und somit kein Viereck mehr. Überschneiden sich bei vier Eckpunkten zwei Seiten, so entstehen zwei verschiedene Flächen. Ein Viereck besteht aber immer nur aus einer Fläche.
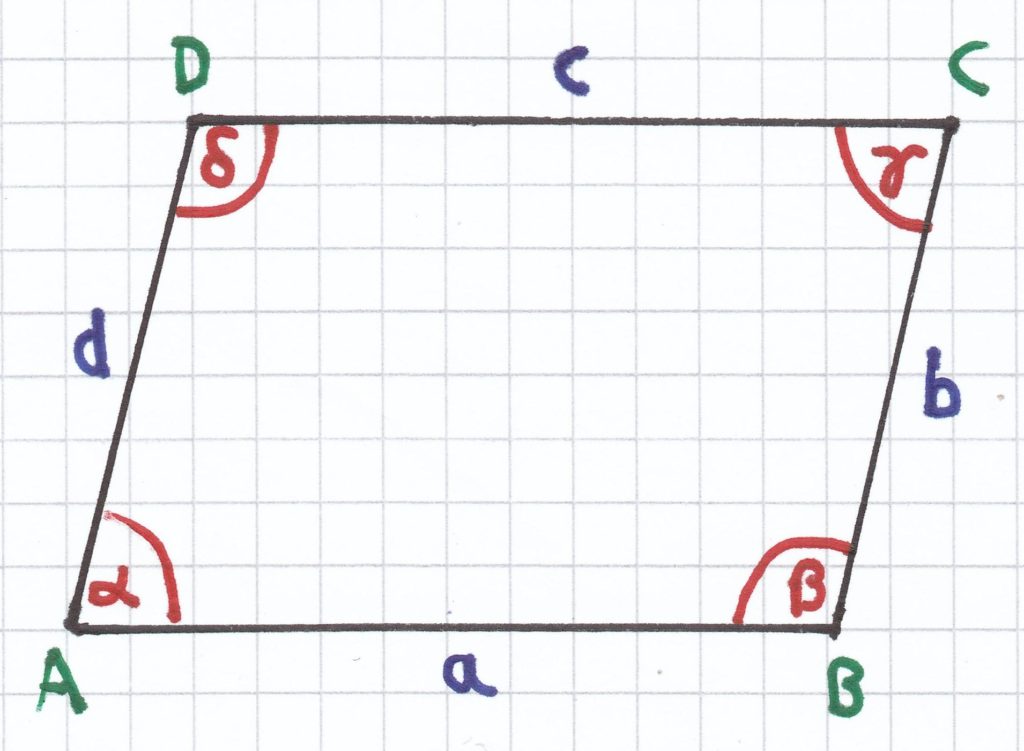
3. In einem Viereck ABCD nennt man die Innenwinkel α (Alpha), β (Beta), γ (Gamma), δ (Delta). Hierbei befindet sich der Winkel α am Eckpunkt A, der Winkel β am Eckpunkt B, der Winkel γ am Eckpunkt C und der Winkel δ am Eckpunkt D.
Die Seitenlinie zwischen den Eckpunkten A und B bezeichnet man als a, die Seitenlinie zwischen den Eckpunkten B und C als b, die Seitenlinie zwischen den Eckpunkten C und D als c und die Seitenlinie zwischen den Eckpunkten D und A als c. Die Diagonale zwischen den Eckpunkten A und C bezeichnet man als e und die Diagonale zwischen den Eckpunkten B und D als f.
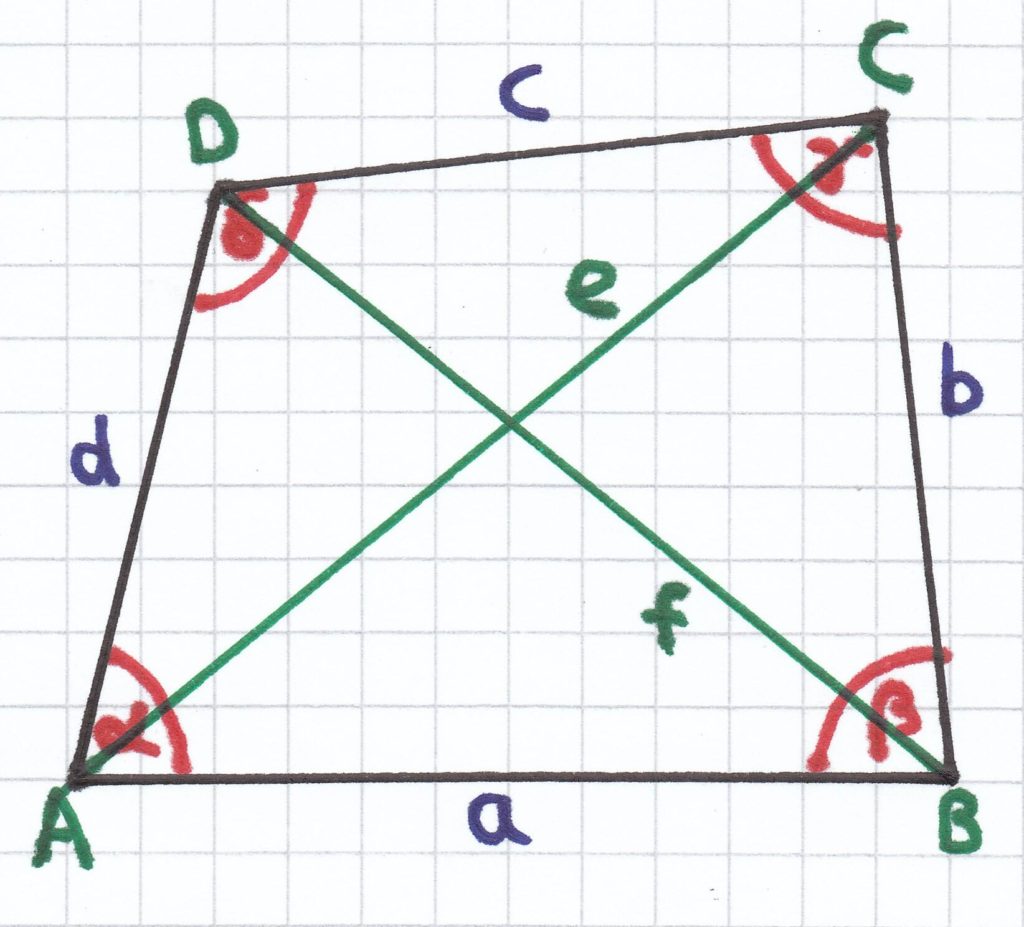
Als Stücke des Vierecks werden die Seiten, die Diagonalen und die Innenwinkel bezeichnet.
Wie bei allen anderen Vielecken erfolgt die Beschriftung eines Vierecks immer „gegen den Uhrzeigersinn“.
2. Definitionen besonderer Vierecke
Ein allgemeines Viereck ist ein Viereck, wie es oben zu sehen ist. Darüber hinaus gibt es in der Mathematik aber auch noch verschiedenartige besondere Vierecke.
Damit ein besonderes Viereck vorliegt, müssen bestimmte Beziehungen im Viereck vorliegen.
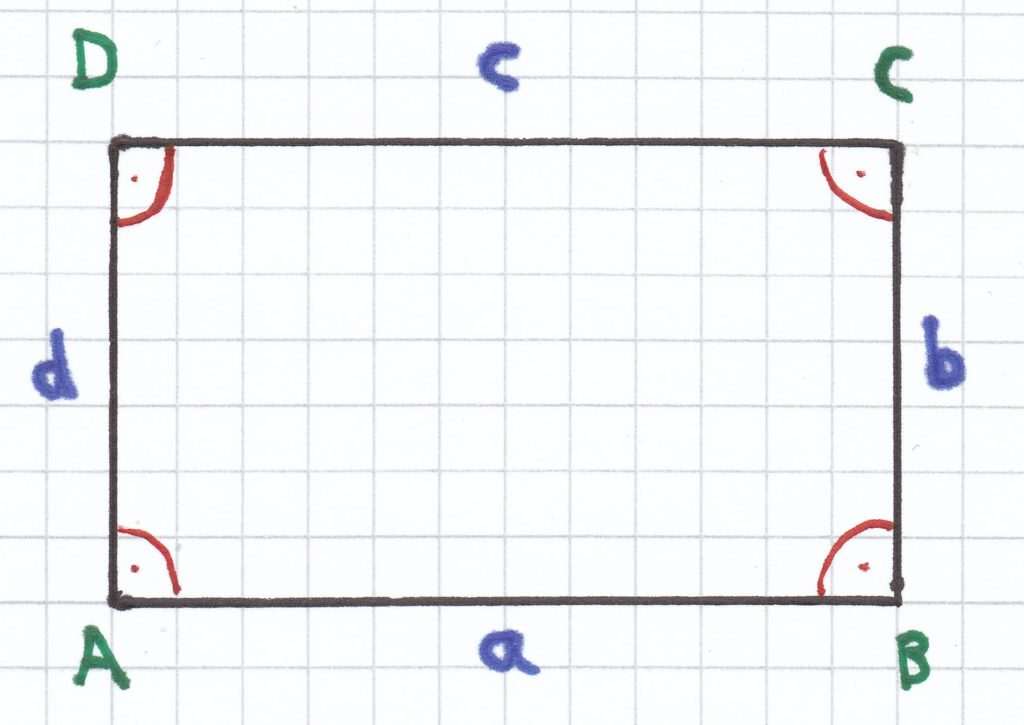
2.1 Ein Rechteck
Definition eines Rechtecks: Sind in einem Viereck alle Winkel rechtwinklig, so liegt ein Rechteck vor.
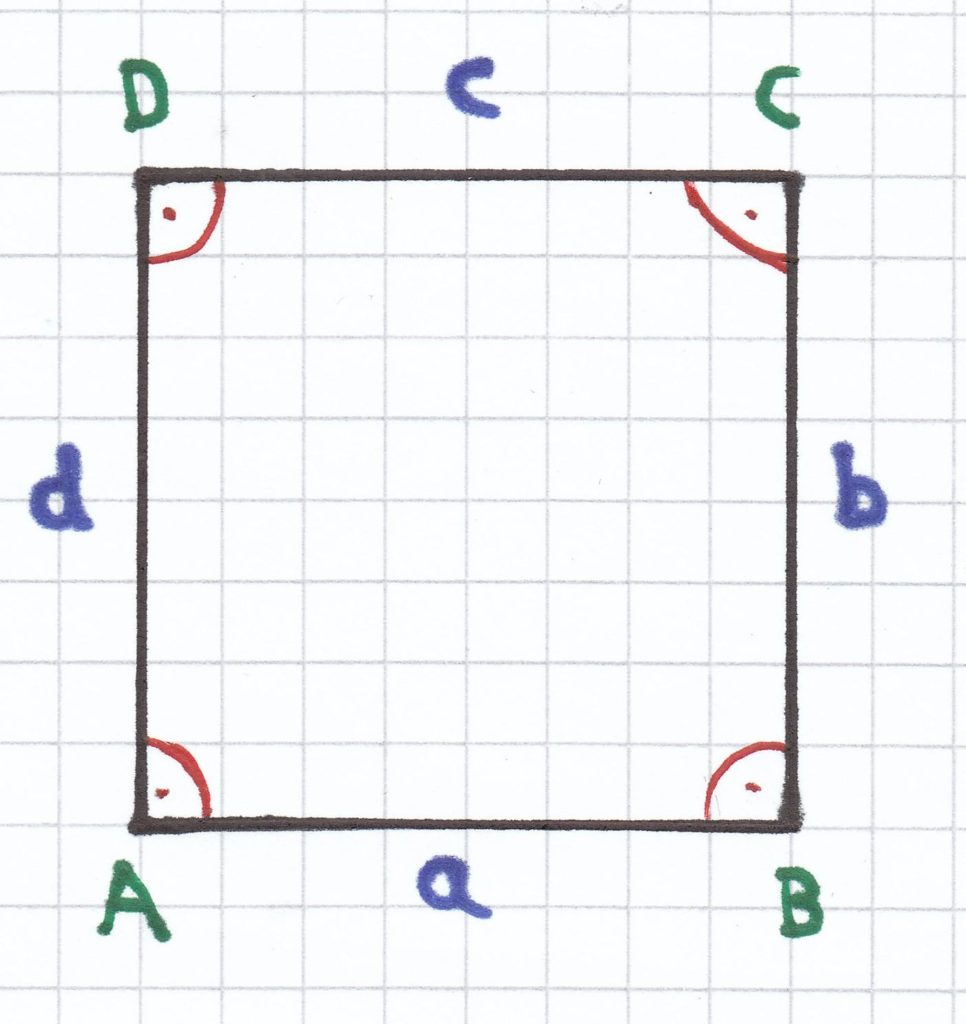
2.2 Ein Quadrat
Definition eines Quadrats: Sind bei einem Viereck alle Seiten gleich lang und im Viereck alle Winkel rechtwinklig, so liegt ein Quadrat vor.
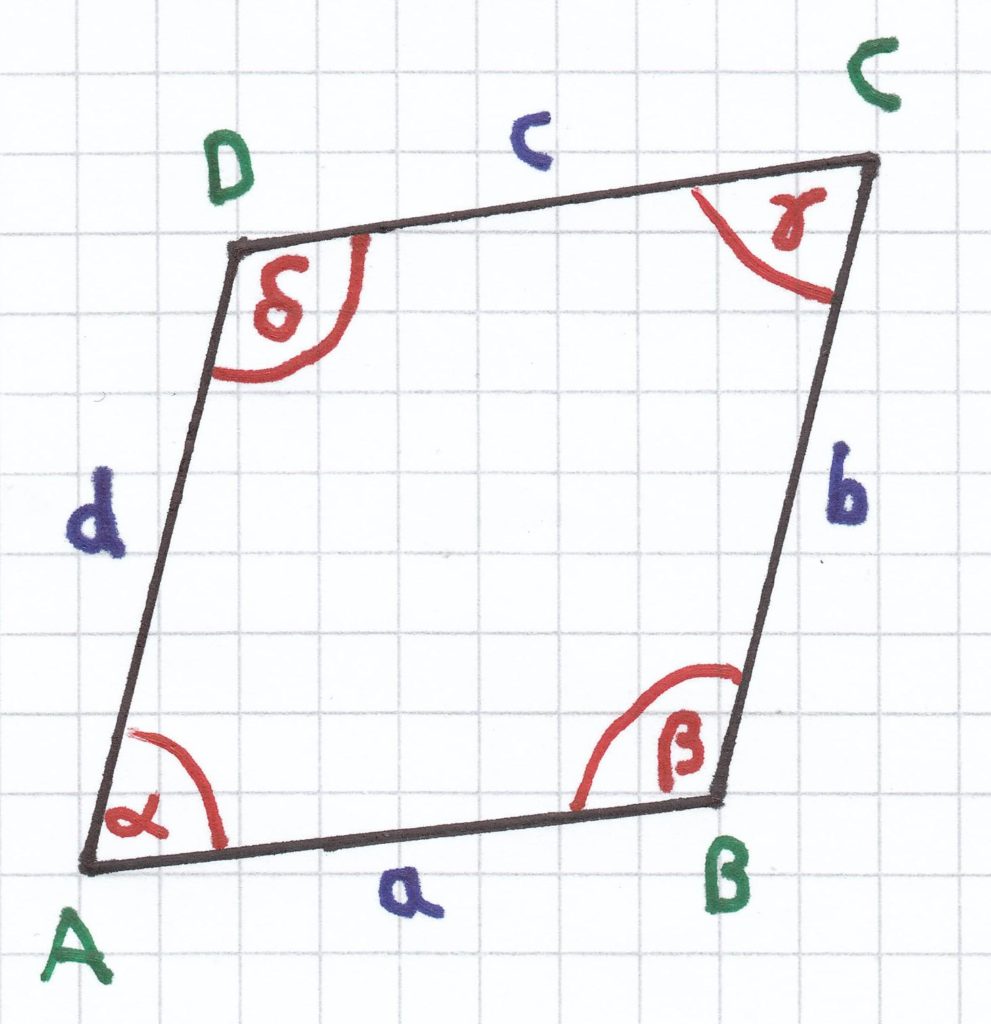
2.3 Eine Raute bzw. Rhombus
Definition einer Raute bzw. Rhombus: Sind bei einem Viereck alle Seiten gleich lang, dann liegt eine Raute bzw. ein Rhombus vor.
2.4 Ein Parallelogramm
Definition eines Parallelogramms: Sind bei einem Viereck die gegenüberliegenden Seiten parallel zueinander, dann liegt ein Parallelogramm vor.