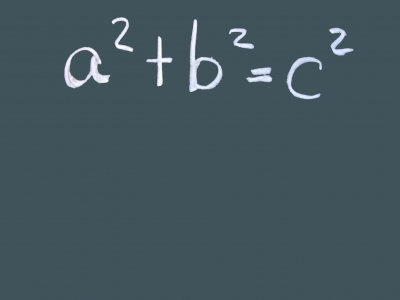
1. Allgemeines und Beweisführung zum Satz des Pythagoras
Eine der berühmtesten Gesetzmäßigkeiten in der Mathematik ist der Satz des Pythagoras, da dieser bereits in der vorchristlichen Antike bekannt war und bis heute die am meisten bewiesene Gesetzmäßigkeit der Mathematik-Geschichte ist.
Bei dem Satz des Pythagoras handelt es sich um eine Flächengleichung, die an jedem rechtwinkligen Dreieck aufgestellt werden kann. Der Satz des Pythagoras besagt nämlich: Die aus der Länge einer Hypotenuse erzeugte quadratische Fläche ist gleich der quadratischen Flächen, die durch die Längen der Katheten gebildet werden. Daraus ergibt sich folgende berühmte Gleichung für den Satz des Pythagoras:
c2 = a2 + b2
Im Umkehrschluss ergibt sich hierdurch, dass jedes Dreieck rechtwinklig ist, das diese Gleichung erfüllt.
Nachfolgend ist der Satz des Pythagoras bildlich dargestellt.
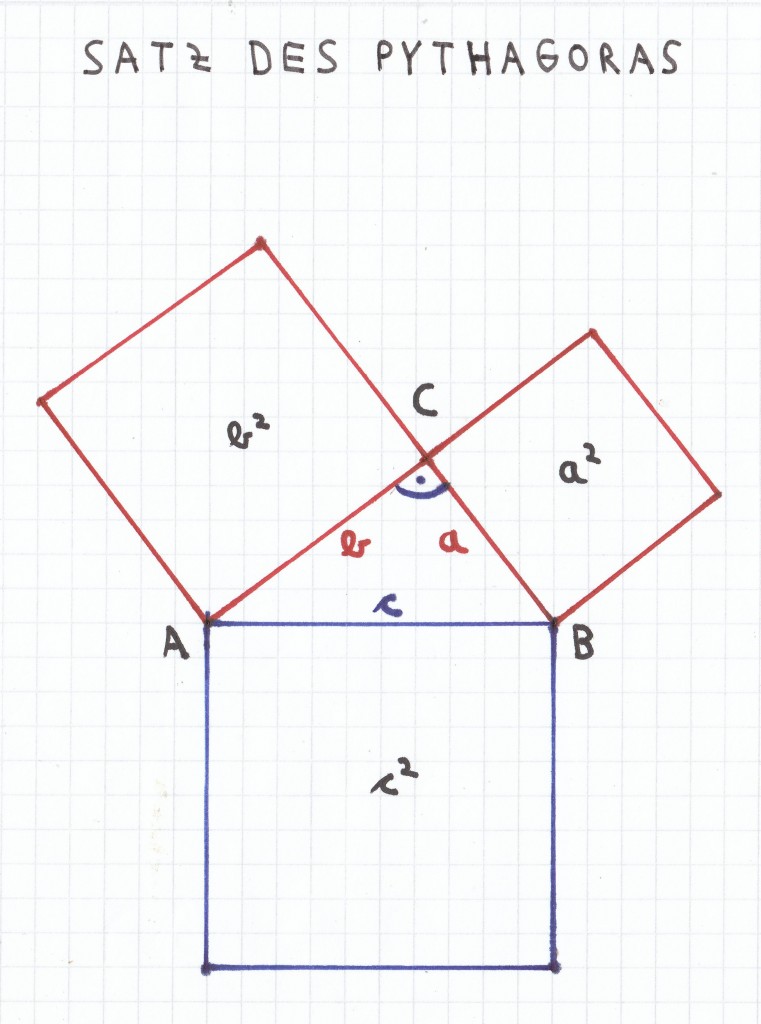
Die Hypotenuse c des rechtwinkligen Dreiecks ABC beträgt hier 5 cm, die Kathete b hat die Länge 4 cm und die Kathete a die Länge 3 cm.
Quadriert man nun alle Seitenlängen, dann ergeben sich die einzelnen Flächenquadrate c2 = 25 cm2, b2 = 16 cm2 und a2 = 9 cm2.
Hierbei kann man sehen, dass im rechtwinkligen Dreieck die Summe der quadrierten Katheten gleich der quadrierten Hypotenuse ist. Denn:
(4 cm)2 + (3 cm)2 = (5 cm)2
16 cm2 + 9 cm2 = 25 cm2
25 cm2 = 25 cm2
Vom Satz des Pythagoras gibt es mehrere Hundert (!) verschiedene Beweise, die seine Richtigkeit belegen. Hier sollen uns ein geometrischer und ein rechnerischer Beweis jedoch genügen, um dessen mathematische Gesetzmäßigkeit als wahr zu bestätigen.
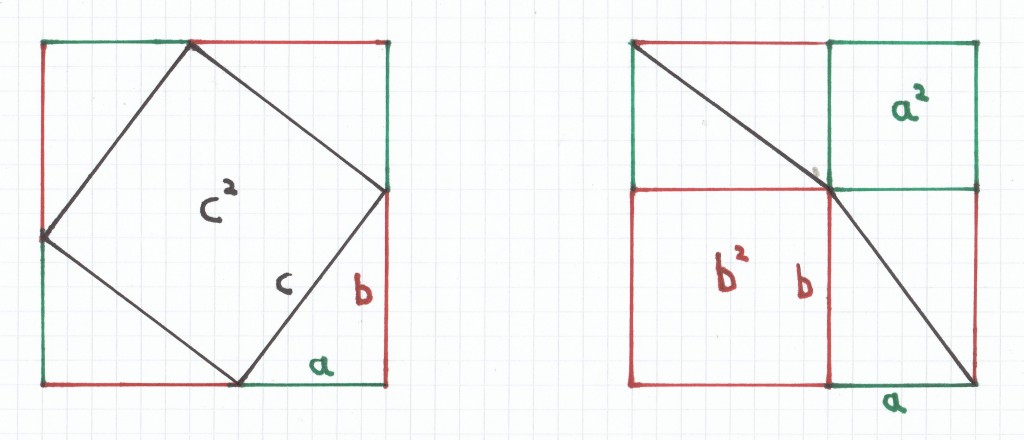
Das konstruierte Quadrat auf der rechten Seite hat die Seitenlänge a + b (a ist der grüne Strich, b der rote, a = 3 cm, b = 4 cm). In das Quadrat werden jeweils an seinen Ecken vier gleich große, deckungsgleiche/kongruente Dreiecke, die aus den Katheten a und b bestehen eingezeichnet. Hierbei sind alle Dreiecke rechtwinklig. Aus den jeweiligen Hypotenusen der einzelnen Dreiecke entsteht so ein Quadrat im Quadrat, das den Flächeninhalt c2 besitzt (Hypotenuse mal Hypotenuse bzw. c · c).
Das konstruierte Quadrat auf der linken Seite hat ebenfalls die Seitenlänge a + b (a ist wiederum der grüne Stich, b wiederum der rote, a = 3 cm, b = 4 cm). In dieses Quadrat werden nun jeweils oben links und unten rechts zwei deckungsgleiche/kongruente Dreiecke, die ebenfalls aus den Katheten a und b bestehen, eingezeichnet. Hierbei sind natürlich wiederum alle Dreiecke auch rechtwinklig. Aufgrund der so gewählten Konstruktion der einzelnen Dreiecke entstehen nun unten links ein Quadrat mit der Seitenlänge b (aus den Katheten b der Dreiecke) und oben rechts ein Quadrat mit der Seitenlänge a (aus den Katheten a der Dreiecke). Das Quadrat mit der Seitenlänge b hat folglich den Flächeninhalt b2 (Kathete mal Kathete bzw. b · b), das Quadrat mit der Seitenlänge a demzufolge den Flächeninhalt a2 (Kathete mal Kathete bzw. a · a).
Da das konstruierte Quadrat links gleich viele deckungsgleiche/konkruente Dreiecke wie das rechte konstruierte Quadrat vorweist, ist die Fläche der hierdurch im Innern entstehenden Quadrate gleich groß und demzufolge gilt:
c2 = a2 + b2
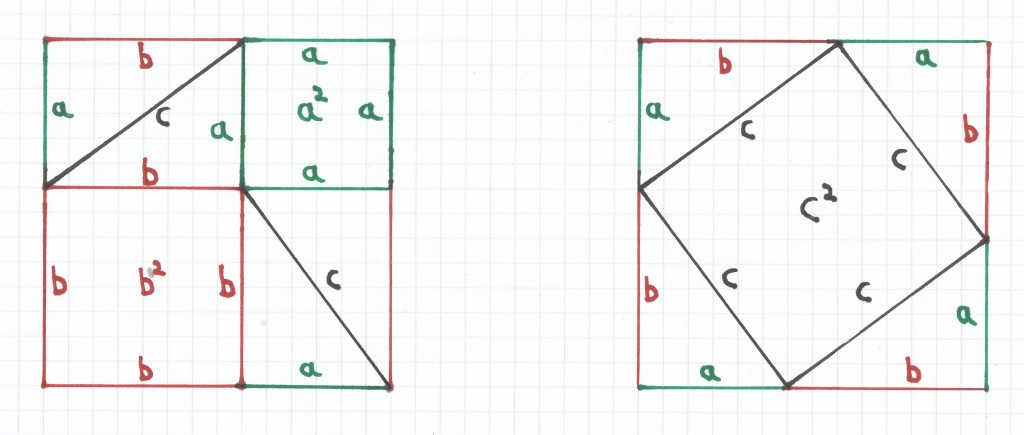
Auf dem obigen Bild sind wieder zwei große Quadrate zu sehen, die sich wiederum jeweils aus den Seitenlängen a + b zusammensetzen (a ist der grüne Strich mit a = 3 cm und b ist der rote Strich mit b = 4 cm).
Innerhalb des linken Quadrates mit der Seitenlänge a + b sind am oberen rechten Ende und am unteren rechten Ende jeweils 2 deckungsgleiche/kongruente Dreiecke eingezeichnet worden. Hierdurch entstand unten links ein Quadrat mit dem Flächeninhalt b2 (Kathete mal Kathete bzw. b · b) und oben rechts ein Quadrat mit dem Flächeninhalt a2 (Kathete mal Kathete bzw. a · a). Innerhalb des rechten Quadrates wurden jeweils an den Ecken des Quadrats 1 deckungsgleiches/konkruentes Dreieck eingezeichnet. Dadurch entstand im Innern ein Quadrat mit dem Flächeninhalt c2 (Hypotenuse mal Hypotenuse bzw. c · c).
Da der Flächeninhalt des rechten und des linken Quadrates gleich ist, kann man beide Quadrat-Flächeninhalte mittels einer Gleichung gegenüberstellen.
Hierbei lässt sich der linke Flächeninhalt des Quadrats mit dem Term (a + b) · (a + b) bzw. (a + b)2 wiedergegeben (was nichts anderes als die 1. Binomische Formel ist). Der rechte Flächeninhalt des Quadrats setzt sich aus 4 deckungsgleichen/kongruente Dreiecken plus einem Quadrat in der Mitte zusammen. Die Fläche eines Dreiecks kann man mit der Formel Grundseite mal Höhe geteilt durch 2 bzw.
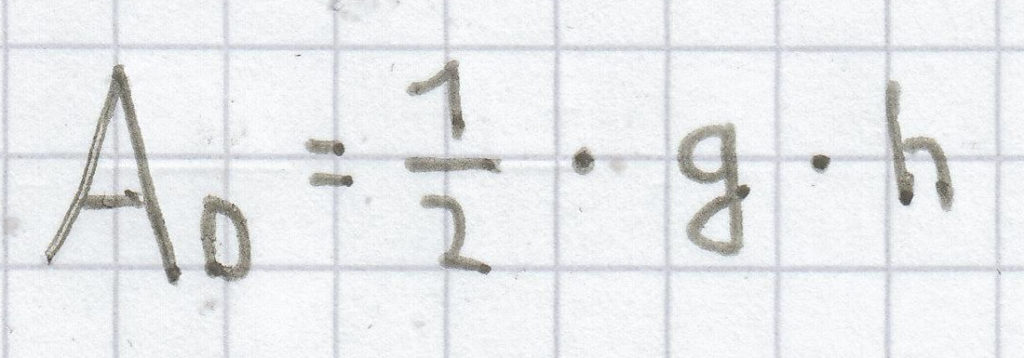
wiedergeben. Bezogen auf eines der deckungsgleichen/kongruenten Dreicke ergibt sich somit
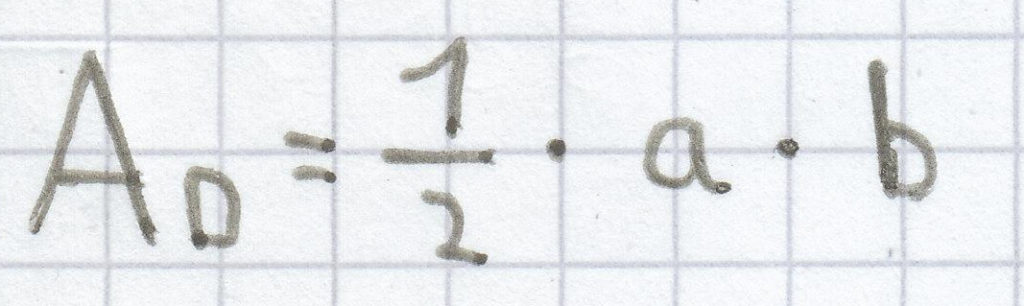
. Der Flächeninhalt des rechten Quadrats kann man mit diesem Term wiedergegeben:
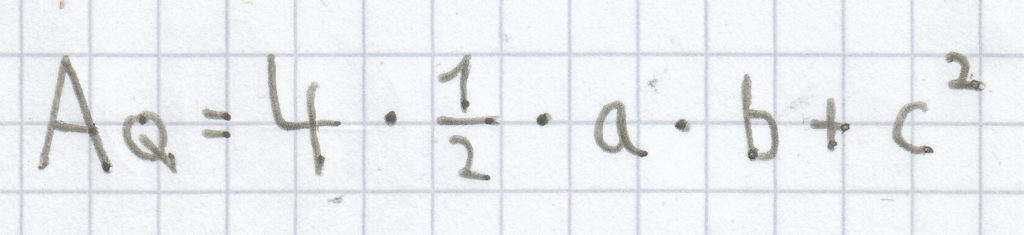
(die „4″ vor dem ersten Einzelterm ergibt sich durch den 4-fachen Flächeninhalt der 4 vorhanden Dreiecke).
Nun kann man folgende Gleichung für den Flächeninhalt des rechten und des linken Quadrats aufstellen.
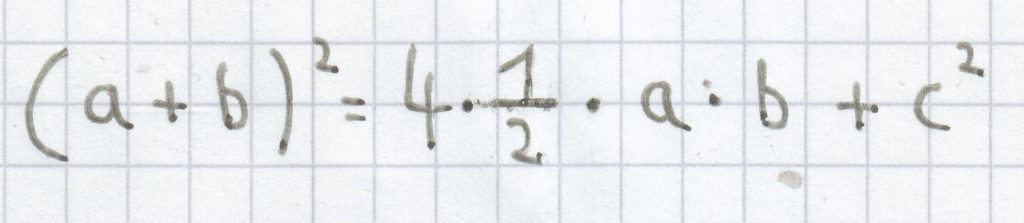
Durch Auflösen der 1. Binomischen Formel ergibt sich der linke Term. Bei dem rechten Term kann man den Bruch kürzen.
a2 + 2ab + b2 = 2ab + c2 | – 2ab
Nach Eliminierung des Termes 2ab ergibt sich der Satz des Pythagoras und somit der rechnerische Beweis, dass die Fläche der beiden Quadrate im Innern des linken Quadrats gleich der Fläche des Quadrates im Innern des rechten Quadrates ist.
a2 + b2 = c2
2. Separieren und Auflösen der Flächenquadrate
Um den Satz des Pythagoras anwenden zu können, muss zunächst innerhalb der Gleichung das jeweils gesuchte Flächenquadrat separiert werden und anschließend aufgelöst werden. Da beim Satz des Pythagoras drei verschiedene Flächenquadrate (die quadrierte Hypotenuse und die beiden quadrierten Katheten) beziehungsweise drei verschiedene Variable vorkommen, gibt es drei unterschiedliche Möglichkeiten die Gleichung aufzulösen. Bei dem folgenden Separieren und Auflösen der Flächenquadrate wird davon ausgegangen, dass innerhalb des rechtwinkligen Dreiecks der Hypotenuse die Seitenlänge c zugeordnet ist und den beiden Katheten die Seitenlänge a und die Seitenlänge b.
Anmerkung: Je nach Aufgabenstellung kann in einem rechtwinkligen Dreieck die Hypotenuse auch eine andere Seitenlängenbezeichnung haben und demzufolge auch die beiden Katheten. Nichtsdestotrotz gilt dann natürlich trotzdem der Satz des Pythagoras.
1. Möglichkeit der Gleichungsauflösung:
c2 = a2 + b2 | √
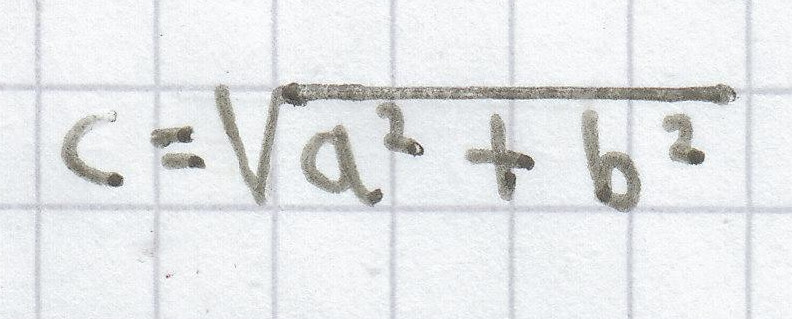
2. Möglichkeit der Gleichungsauflösung:
c2 = a2 + b2 | – b2
c2 – b2 = a2 | √
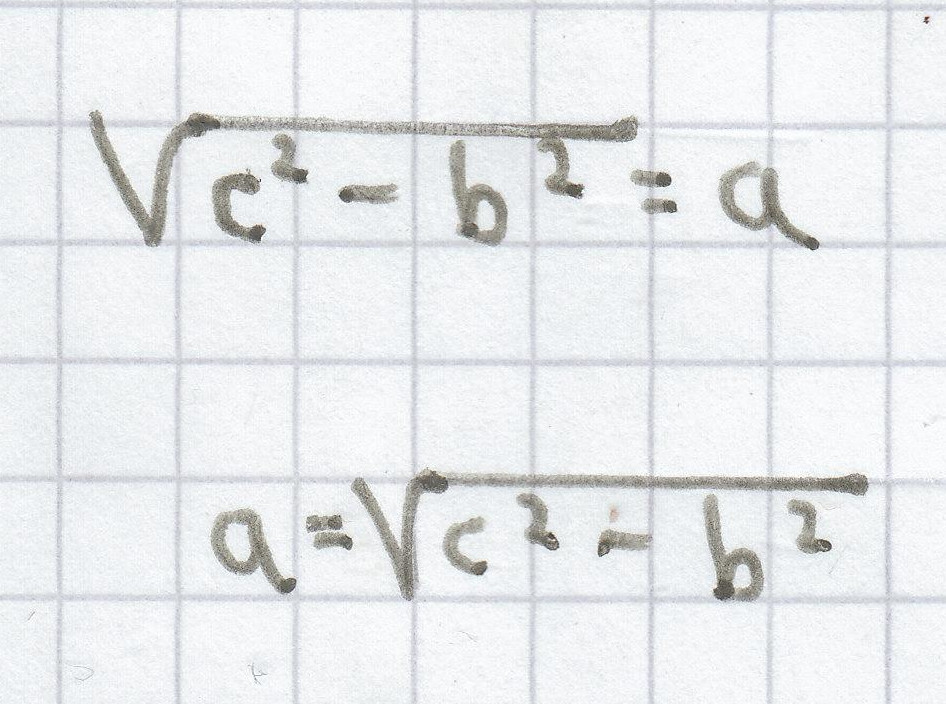
3. Möglichkeit der Gleichungsauflösung:
c2 = a2 + b2 | – a2
c2 – a2 = b2 | √
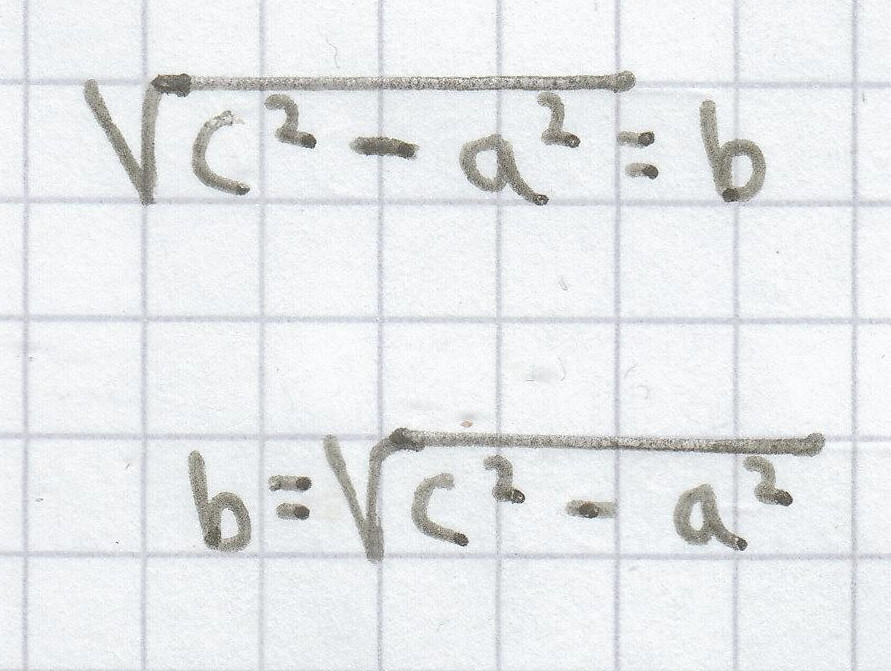
Da beim Satz des Pythagoras immer Flächenquadrate vorkommen, die auf positiven Seitenlängen basieren, muss beim Ziehen der Wurzel keine Fallunterscheidung gemacht werden.
Beispiele zu den drei Gleichungsauflösungen
1. Es ist ein rechtwinkliges Dreieck gegeben, bei dem die Seitenlänge der Kathete a = 3 cm und die der Kathete b = 4 cm betragen. Gesucht ist die Seitenlänge der Hypotenuse c. Über die 1. Gleichheitsauflösung,
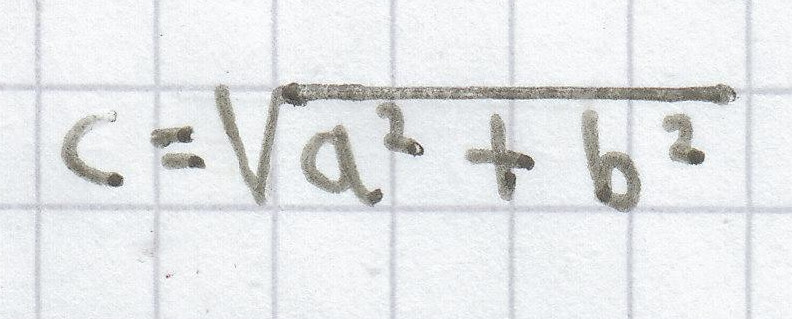
, kann man nun ganz einfach c berechnen, indem man einfach in die beiden Variablen der Katheten a und b die hierfür angegeben Wert einsetzt.
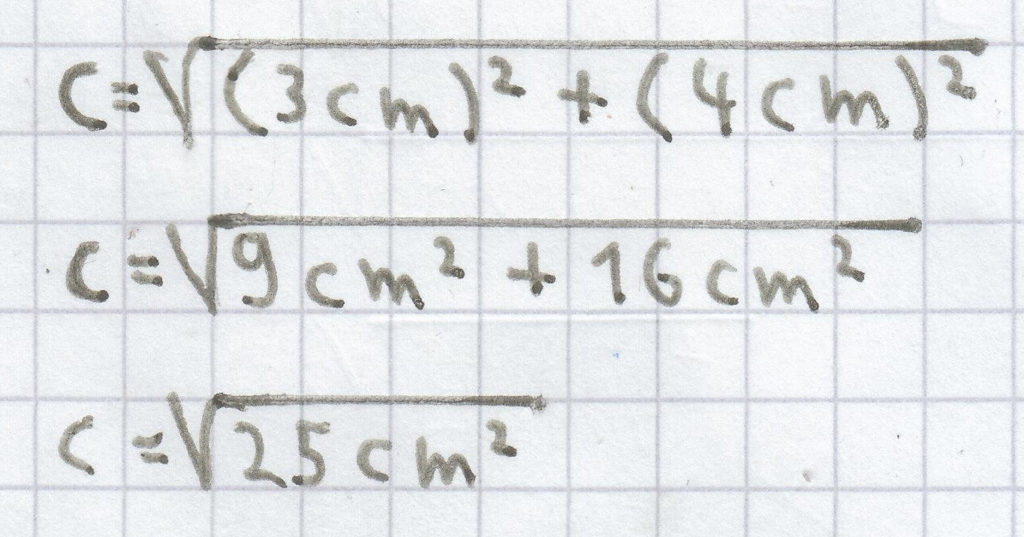
c = 5 cm
Beim Einsetzen der Werte in die Variablen sollte man immer eine Klammer um den Wert und der dazugehörigen Einheit machen. Dadurch wird eindeutig sichtbar, dass sowohl die „nackte“ Zahl als auch die Einheit quadriert werden.
2. Es ist ein rechtwinkliges Dreieck gegeben, bei dem die Seitenlänge der Hypotenuse c = 15 cm und die Seitenlänge der Kathete b = 5 cm betragen. Gesucht ist die Seitenlänge der Kathete a. Die Seitenlänge a kann man nun problemlos mit der 2. Gleichheitsauflösung berechnen. Hierbei muss man wiederum nur die gegebenen Werte in die beiden Variablen einsetzen.
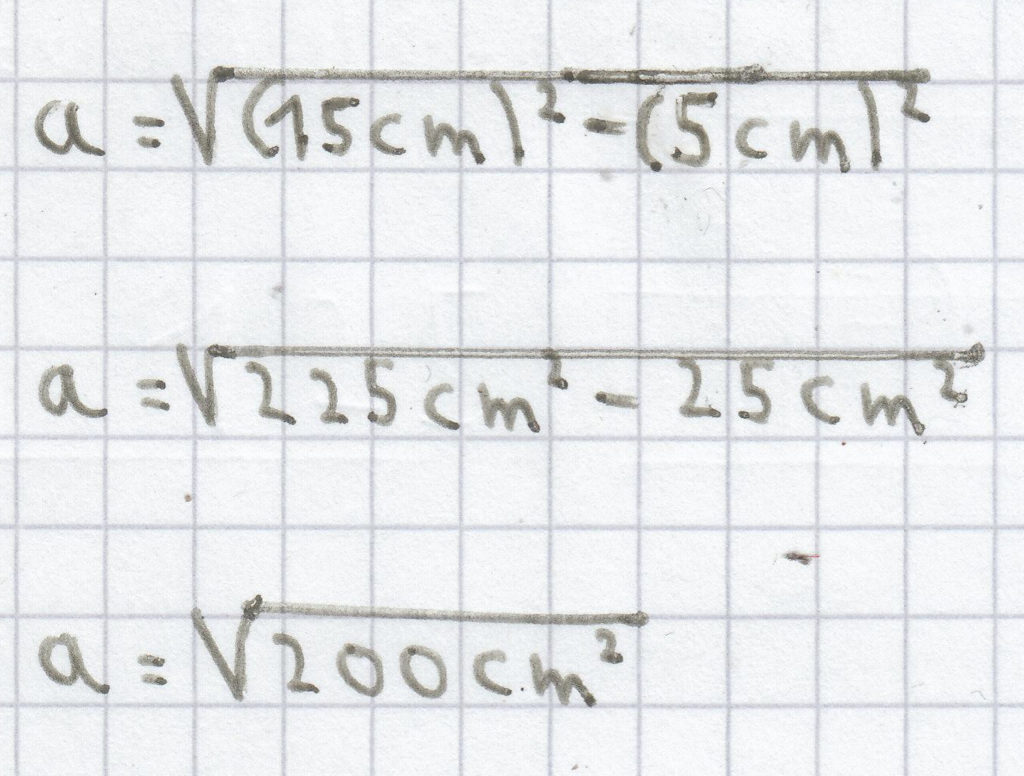
a = 14,14 cm (gerundet auf die 2. Nachkommastelle)
3. Es ist ein rechtwinkliges Dreieck gegeben, bei dem die Seitenlänge der Hypotenuse c = 20,8 cm und die Seitenlänge der Kathete a = 12,3 cm betragen. Gesucht ist die Seitenlänge der Kathete b. Die Seitenlänge b kann nun wieder mittels der 3. Gleichheitsauflösung recht einfach ermittelt werden.
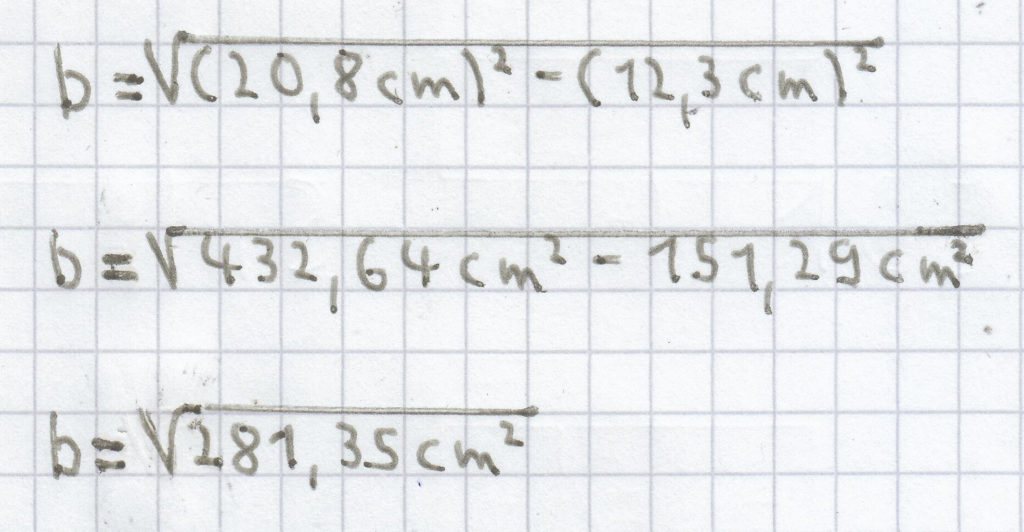
b = 16,77 cm (gerundet auf die 2. Nachkommastelle)
3. Beweisführung für die Umkehrung vom Satz des Pythagoras
Bisher wurde nur bewiesen, dass für ein rechtwinkliges Dreieck ABC der Satz des Pythagoras, c2 = a2 + b2, gilt. Wie sieht das aber für den Kehrsatz aus, d. h. wenn drei Seiten eines Dreiecks gegeben sind. Ist dann auch das Dreieck rechtwinklig, wenn durch Quadrieren der einzelnen Seiten die Flächengleichung a2 + b2 = erfüllt ist? Die Antwort lautet: „ja“
Folgende drei Bilder beweisen hierbei die Gültigkeit für die Umkehrung vom Satz des Pythagoras.
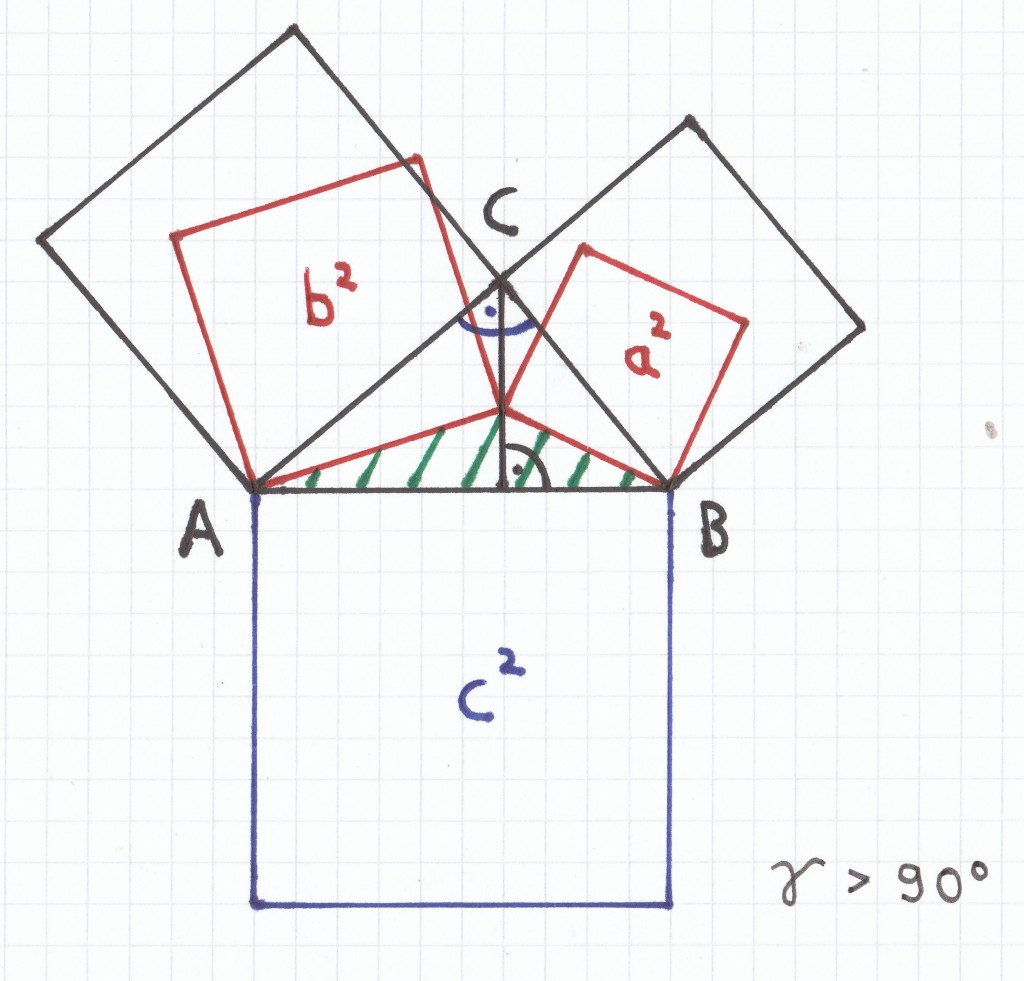
Bei dem ursprünglichen rechtwinkligen Dreieck ABC, bei dem γ = 90˚ beträgt, wird der Punkt C senkrecht nach unten verschoben. Hierdurch entsteht das neue grün gestrichelte Dreieck, das nun einen stumpfwinkligen Winkel γ vorweist (γ > 90˚). Bei diesem neuen grün gestrichelten Dreieck bleibt die quadrierte Fläche c² der Seitenlänge c unverändert, die quadrierten Flächen a² und b² der Seitenlänge a und b werden hierbei aber kleiner (auf dem Bild sind dies die roten Quadrate). Demzufolge gilt für die neuen Flächenquadrate des stumpfwinkligen Dreiecks: a2 + b2 < c2.
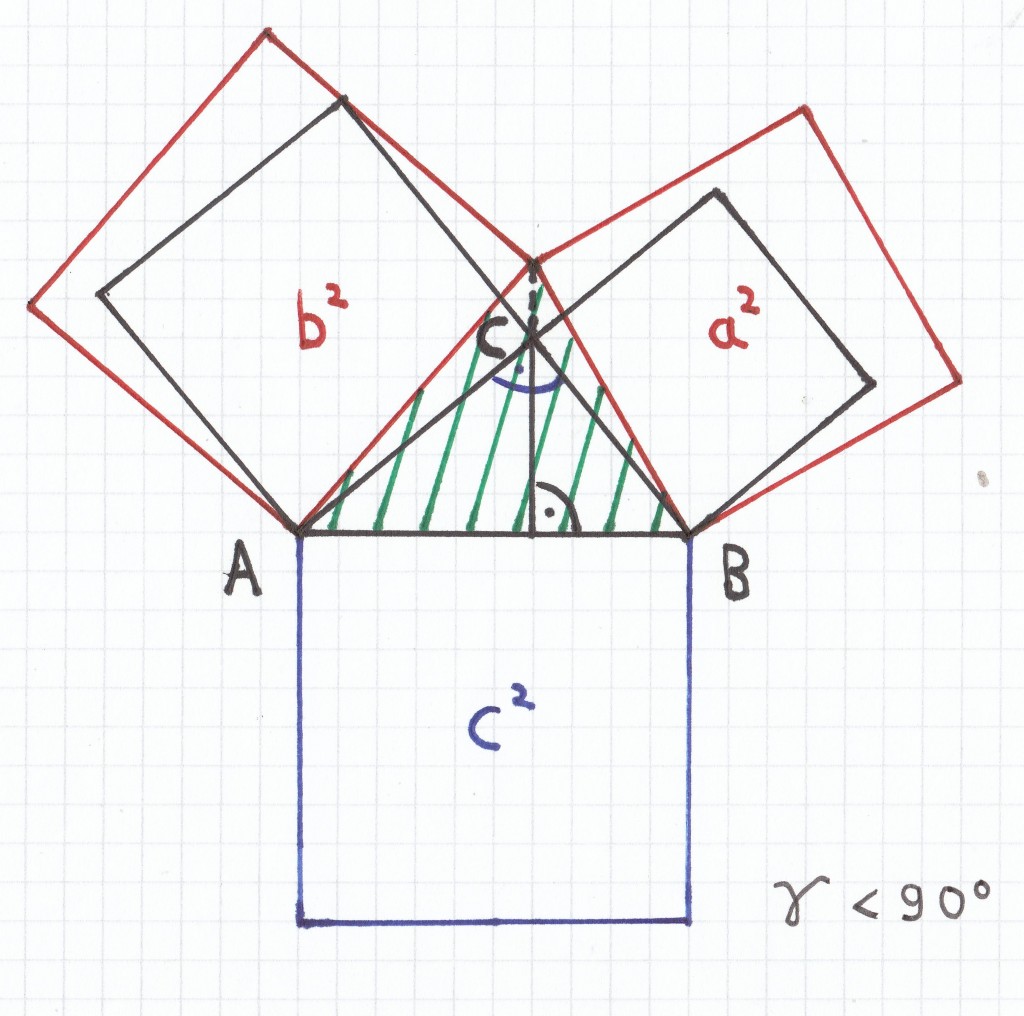
Bei dem ursprünglichen rechtwinkligen Dreieck ABC, das den rechten Winkel γ = 90˚ vorweist, wird der Punkt C senkrecht nach oben verschoben. Dadurch entsteht das neue grün gestrichelte Dreieck, das nun eine spitzen Winkel γ hat (γ < 90˚). Bei dem neuen, grün gestrichelten Dreieck bleibt wiederum die quadrierte Fläche c2 der Seitenlänge c unverändert, die quadrierten Flächen a2 und b2 der Seitenlängen a und b werden dabei aber größer (auf dem Bild sind dies wiederum die roten Quadrate). Folglich gilt für die neuen Flächenquadrate des spitzwinkligen Dreiecks: a2 + b2 > c2.
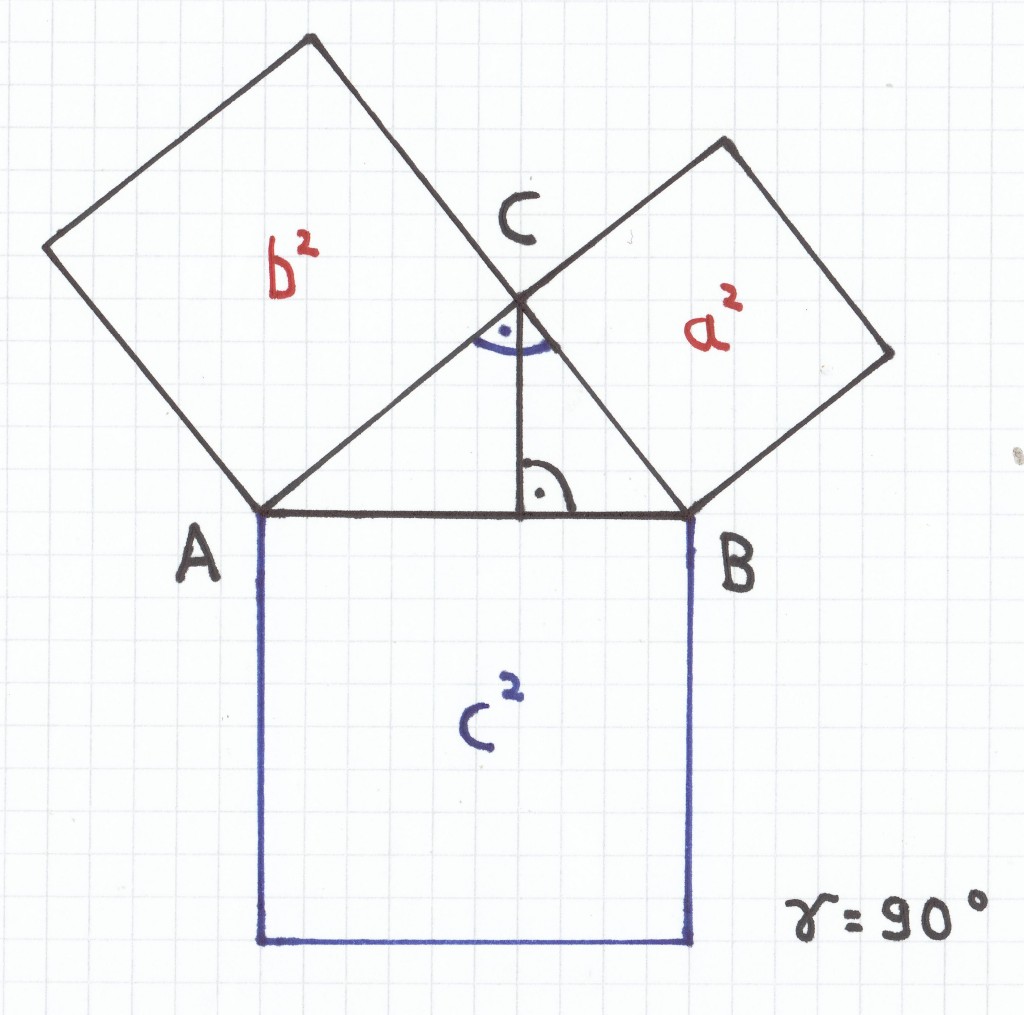
Aus der 1. und 2. Beweisführung ergibt sich folglich die 3. Beweisführung: Wenn der Winkel γ ≠ 90˚ ist, dann gilt immer c2 ≠ a2 + b2. Demzufolge ist nur bei γ = 90˚ geben, dass c2 = a2 + b2 ist.
Daher gilt als Umkehrsatz vom Satz des Pythagoras:
Bei jedem Dreieck ABC, bei dem die Flächengleichung c2 = a2 + b2 erfüllt ist, ist γ = 90˚.
Ist hingegen c2 > a2 + b2, dann ist γ immer > 90˚ und γ weist demzufolge einen stumpfen Winkel auf.
Ist hingegen c2 < a2 + b2, dann ist γ immer < 90˚ und γ weist folglich einen spitzen Winkel auf.
Beispiele:
Gegeben sind folgenden Dreiecke ABC:
a) a = 5 cm, b = 3 cm, c = 8 cm;
b) a = 4 cm, b = 3 cm, c = 2 cm;
c) a = 6 cm, b = 8 cm, c = 10 cm.
Überprüfe mittels des Kehrsatzes vom Satz des Pythagoras, welches dieser Dreieck rechtwinklig, spitzwinklig und stumpfwinklig ist.
a) Hier kann man bereits sehen, dass es sich mit ziemlicher Sicherheit um ein stumpfwinkliges Dreieck handelt. Denn c ist um einiges größer als a und b. Der Kehrsatz vom Satz des Pythagoras bestätigt dies auch: (5)2 + (3)2 < (8)2 = 25 + 9 < 64 = 34 < 64
Daher handelt es sich hier eindeutig um ein stumpfwinkliges Dreieck.
b) Hier kann man bereits sehen, dass dass es sich mit ziemlicher Sicherheit um ein rechtwinkliges Dreieck handel. Denn c ist kleiner als a und b. Der Kehrsatz vom Satz des Pythagoras bestätigt dies auch: (4)2 + (3)2 > (2)2 = 16 + 9 > 4 = 25 > 4.
Daher handelt es sich hier eindeutig um ein spitzwinkliges Dreieck.
c) Bei diesem Dreieck ist noch nicht gleich zu sehen, um was für ein Dreieck es sich handelt. Denn c ist zwar größer als a und b, aber nicht entschieden. Der Kehrsatz bestätigt dies: (6)2 + (8)2 = (10)2 = 36 + 64 = 100 = 100 = 100
Da die Summe der quadrierten Seitenlängen a und b gleich groß ist der quadrierten Seitenlänge c, handelt es sich hier eindeutig um ein rechtwinkliges Dreieck.