Prismen

1. Allgemeines zu Prismen

Eine dreidimensionale Figur bezeichnet man in der Mathematik als einen Körper. Hierbei unterscheidet man Körper nach folgendem Kriterium: Sind die Grund- und Deckflächen eines Körpers ein Vieleck und zueinander kongruent/deckungsgleich, dann liegt ein sogenanntes Prisma vor. Alle anderen Körper, die dieses Kriterium nicht erfüllen, sind keine Prismen.

Primsen werden auch als Säulen bezeichnet.

Die bekanntesten Prismen sind: der Würfel und der Quader.

Bei einem Würfel bestehen alle Flächen aus gleich größen Vierecken; bei einem Quader aus mindestens zwei.

2. Berechnungen bei Prismen

In Mathe können bei Prismen verschiedene Bechnungen durchgeführt werden. Das Volumen bzw. der Rauminhalt des Prismas kann hierbei berechnet werden, ebenso die Oberfläche und die Mantelfläche.

2.1 Volumen/Rauminhalt eines Quaders

Ein Quader besitzt die Kantenlängen a, b, c.

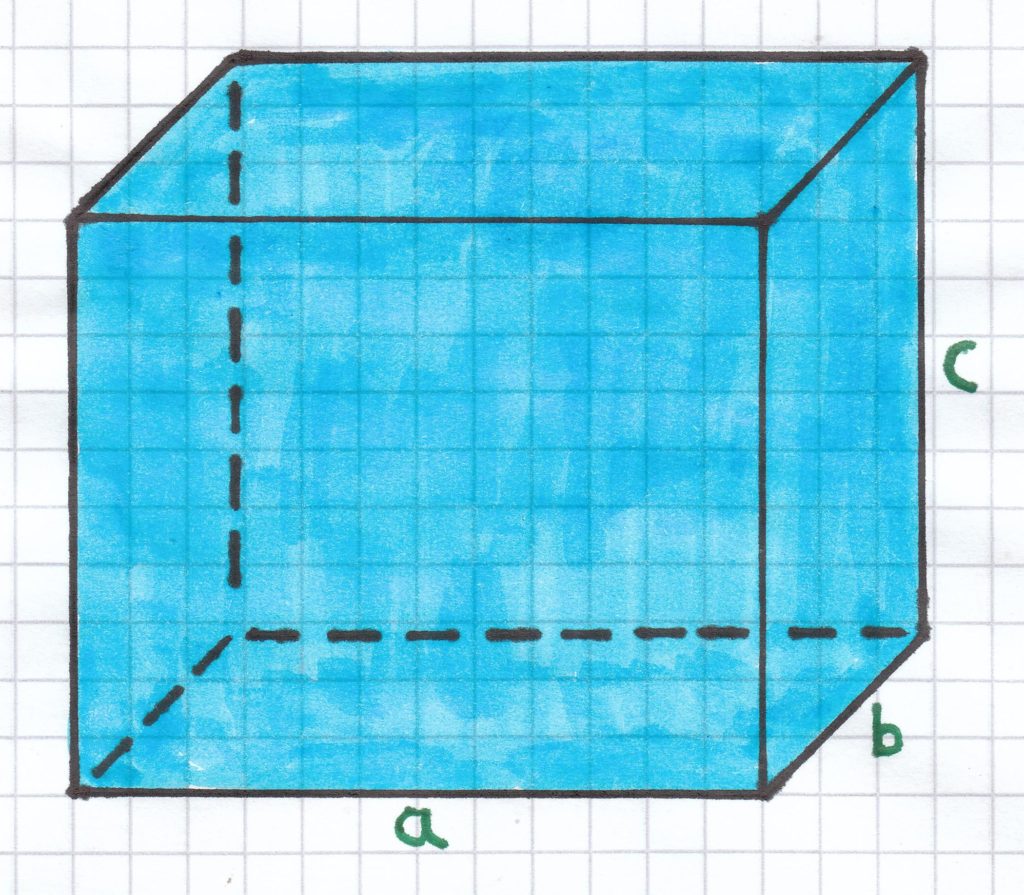
Das Volumen des Quaders ist:

V_Q = a  · b  · c

Beispiel: Ein Quader mit der Kantenlänge a = 6 cm, b = 4 cm und c = 5 cm hat Folgendes Volumen:

V_Q = 6 cm · 4 cm · 5 cm

V_Q = 120 cm³

2.2 Volumen/Rauminhalt eines Würfels

Ein Würfel besitzt die Kantenlänge a = 4 cm.

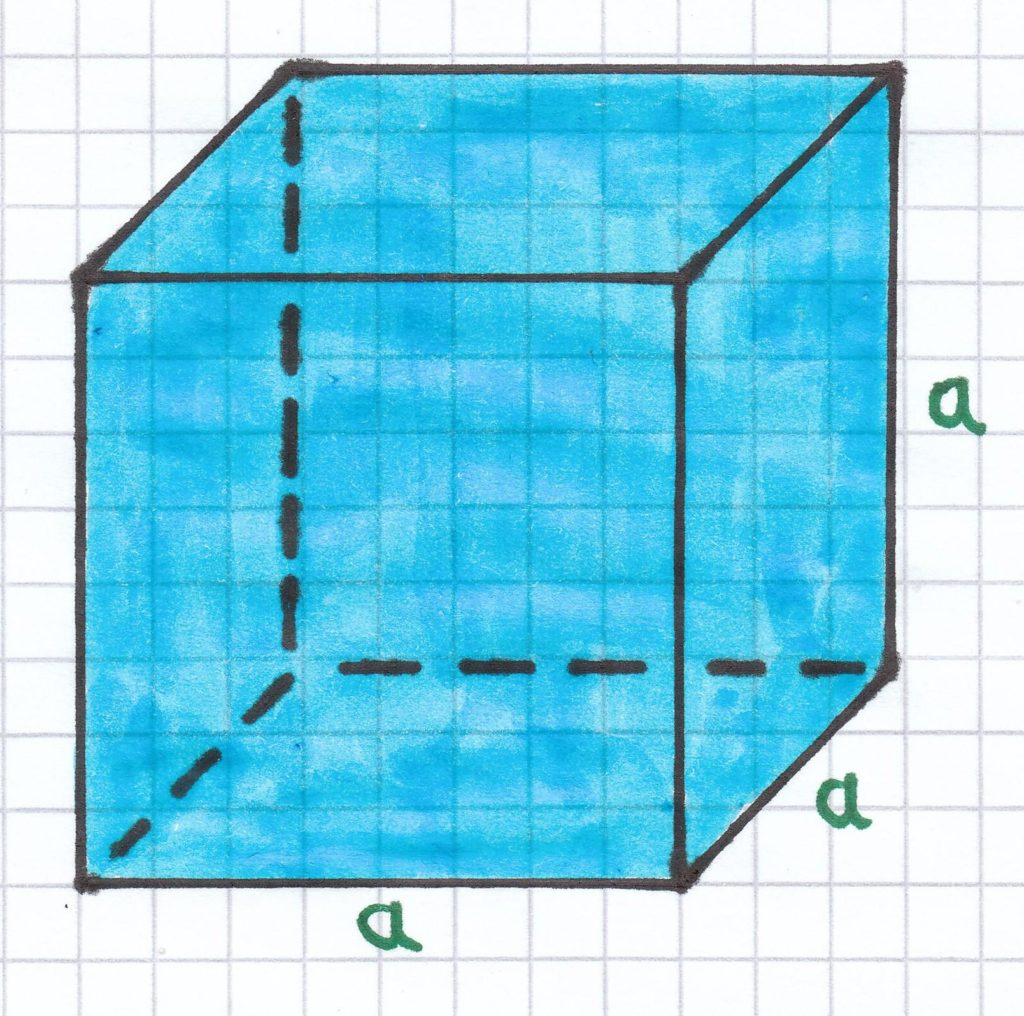
Das Volumen des Würfels beträgt:

V_W = a · a · a

= a³

Beispiel: Ein Würfel mit der Kantenlänge 4 cm hat Folgendes Volumen:

V_W = 4cm · 4 cm · 4 cm

= (4 cm)³

= 64 cm³