
1. Grundlegendes zu Gleichungen
Was eine Gleichung ist, kann man am einfachsten verstehen, wenn man das zentrale mathematische Zeichen bei Gleichungen verstanden hat – das Gleichheitszeichen.
Ein Gleichheitszeichen „verlangt/fordert“ nämlich immer Gleichheit – und das bei allen Gleichungen. Aber zwischen was oder wem? Immer zwischen den beiden Termen, die normalerweise rechts und links des Gleichheitszeichens stehen. Hierbei „verlangt/fordert“ ein Gleichheitszeichen aber von beiden Termen „zeichengemäß“, dass sich ihre mögliche Gleichheit stets absolut eindeutig zeigt – was jedoch nur über den jeweiligen Term-Wert möglich ist. Aus diesem Grund muss man bei einer Gleichung immer zuerst die Variable bestimmen, um eindeutig feststellen zu können – ob das „Verlangen/die Forderung“ des Gleichheitszeichens von den beiden Termen auch wirklich erfüllt wird. Hat man nun die Variable bestimmt und bewiesen, dass rechts und links der Gleichung die Term-Werte gleich groß sind – dann ist das Gleichheitszeichen auch endlich „zufrieden“.

In der Sprache der Mathematik gesprochen heißt das korrekt, dass dann eine Lösung für die Gleichung vorliegt. Denn die Aussage der Gleichung ist dann wahr (wenn nach dem Einsetzen der Lösung in die Gleichung eine wahre Aussage entsteht). Alle Lösungen, die man bei einer jeweiligen Gleichung findet, bilden hierbei schließlich die Lösungsmenge. Die Lösungsmenge stellt immer eine Teilmenge in Bezug auf die Grundmenge der Variablen dar. Ist nichts anderes festgelegt, so ist diese Menge immer ℝ.
Abschließend werden alle Lösungen in der Mathematik wie folgt wiedergegeben: L = {in den geschweiften Klammern stehen alle Lösungen, getrennt durch ein Semikolon und normalerweise zuerst die kleinere Zahl vor der nächst größeren Zahl usw.}, Beispiel: L = {–2; 4}. Hier hat eine Gleichung die Lösungen x = –2 und x = 4.
2. Verschiedene Lösungen von Gleichungen
Je nach Gleichung kann eine Gleichung eine oder mehrere Lösungen haben, unendlich viele Lösungen oder keine Lösung.
2.1 Eine Lösung einer Gleichung
Es ist folgende Gleichung gegeben: 8x + 4 = 20.
Durch Einsetzen verschiedener Zahlen in die Variable kann man nun jeweils überprüfen, wann durch eine Zahl die Gleichung „wahr“ wird. Anhand der Zahlen x = 0, x = 1 und x = 2 soll das nun überprüft werden (hierbei hätte man natürlich auch jede andere Zahl nehmen können, da es vom Definitionsbereich her keine Einschränkung gibt).
Bei x = 0 ergibt sich:
8 · 0 + 4 = 20 <=> 4 = 20.
Das Ergebnis der Gleichung ist „unwahr“ und demzufolge x = 0 keine Lösung dieser Gleichung.
Bei x = 1 ergibt sich:
8 · 1 + 4 = 20 <=> 8 + 4 = 20 <=> 12 = 20.
Wie man unschwer sieht, ist x = 1 auch keine Lösung der Gleichung, da das Ergebnis wiederum „unwahr“ ist.
Bei x = 2 ergibt sich nun:
8 · 2 + 4 = 20 <=> 16 + 4 = 20 <=> 20 = 20.
Jetzt ist das Ergebnis der Gleichung „wahr“, folglich ist x = 2 eine Lösung dieser Gleichung.
Daher ist L = {2}.
Da in dieser Gleichung nur eine Variable mit der Potenz 1 vorkommt (8x bzw. 8x¹), ist dies auch die einzige Lösung der Gleichung.
Das Äquivalenzzeichen/ „<=>“ gibt beim schrittweisen Lösen einer Gleichung jeweils an, dass alle Algebra-Umformungen die Lösungsmenge der Ursprungsgleichung/Ausgangsgleichung nicht verändern.
2.2 Mehrere Lösungen einer Gleichung
Es ist folgende Gleichung gegeben: x² = 4.
Durch Einsetzen der Zahlen x = – 2, x = – 1, x = 0, x = 1, x = 2 soll überprüft werden, welches Lösungen der Gleichung sind.
Bei x = – 2 ergibt sich:
(– 2)² = 4 <=> 4 = 4;
bei x = – 1 ergibt sich:
(– 1)² = 4 <=> 1 = 4;
bei x = 0 ergibt sich:
0² = 4 <=> 0 = 4;
bei x = 1 ergibt sich:
1² = 4 <=> 1 = 4;
bei x = 2 ergibt sich:
2² = 4 <=> 4 = 4.
Wie man schön sieht, sind x = –2 und x = 2 Lösungen der Gleichung.
Daher ist die Lösung hier L = {–2; 2}.
Da in der Gleichung nur eine Variable mit der Potenz 2 (x²) vorkommt, sind diese beiden die einzigen Lösungen der Gleichung.
2.3 Unendlich viele Lösungen einer Gleichung
Je nach Gleichung kann aber auch die Lösungsmenge gleich aller im Definitionsbereich möglichen Zahlen sein, das heißt, dass es hier dann unendlich viele Lösungen gibt.
Folgende Gleichung ist gegeben: 5x + 2 = 5x + 2
Sind beide Terme rechts und links des Gleichheitszeichens absolut gleich, dann gibt es für eine Gleichung immer unendlich viele Lösungen. Denn, egal welchen Wert man in die Variablen einsetzt, das Ergebnis der Gleichung ist immer „wahr“.
Durch Einsetzen beliebiger Zahlen in die Variablen wie beispielsweise x = –12; x = 0; x = 99999 kann dies leicht überprüft werden.
Bei x = –12 ergibt sich:
5 · (–12) + 2 = 5 · (–12) +2 <=> –60 + 2 = –60 + 2 <=> –58 = –58 ;
bei x = 0 ergibt sich:
5 · 0 + 2 = 5 · 0 + 2 <=> 0 + 2 = 0 + 2 <=> 2 = 2;
bei x = 99999 ergibt sich:
5 · 99999 + 2 = 5 · 99999 + 2 <=> 499995 + 2 = 499995 + 2 <=> 499997 = 499997.
Wie man schön sieht, ist jede Zahl, die man in die Gleichung einsetzt, eine Lösung der Gleichung. Denn alle Ergebnisse der Gleichung sind „wahr“. Die Lösungsmenge ist deshalb, abhängig von der Klassenstufe, die größtmögliche Zahlenmenge. Je nach Klassenstufe ist das entweder ℚ oder ℝ und somit hier die Lösung L = ℚ bzw. L = ℝ.
2.4 Keine Lösung einer Gleichung
Aber Gleichungen können auch keine Lösung haben. Dann ist die Lösungsmenge leer.
Folgende Gleichung ist gegeben: 3x + 9 = 3x + 7
Sind beide Variablen rechts und links des Gleichheitszeichens absolut gleich, die anderen rechts und links des Gleichheitszeichens noch vorkommenden Einzelterme jedoch nicht, dann gibt es keine Lösung für die Gleichung. Denn, egal welchen Wert man in die Variablen einsetzt, das Ergebnis ist immer „unwahr“.
Durch beliebige Zahlen wie beispielsweise x = –39; x = 0; x = 12003, die man in die Variablen einsetzt, kann man dies leicht überprüfen.
Bei x = –39 ergibt sich:
3 · (–39) + 9 = 3 · (–39) + 7 <=> –117 + 9 = –117 + 7 <=> –108 = –110;
bei x = 0 ergibt sich:
3 · 0 + 9 = 3 · 0 + 7 <=> 0 + 9 = 0 + 7 <=> 9 = 7;
bei x = 12003 ergibt sich:
3 · 12003 + 9 = 3 · 12003 + 7 <=> 36009 + 9 = 36009 + 7 <=> 36018 = 36016.
Wie man schön sieht, ergibt sich durch jede Zahl, die man in die Variablen einsetzt, ein „unwahres“ Ergebnis. Die Lösungsmenge bleibt deshalb immer leer und die Zahlenmenge ist demzufolge eine leere Menge.
Die Lösung ist daher hier L = { } bzw. L = Ø. Beide Schreibweisen sind in Mathe üblich.
3. Äquivalenzumformungen bei Gleichungen
Normalerweise kann man die Lösung einer Gleichung nicht dadurch ermitteln, dass man „einfach“ verschiedene Zahlen in die vorhandenen Variablen einer Gleichung einsetzt und gewissermaßen so lange herumprobiert, bis man die richtige Lösung gefunden hat. Denn in der Regel ist eine Gleichung aus zahlreichen sehr unterschiedlichen Einzeltermen aufgebaut, so dass man derart eine mögliche Lösung nicht „erahnen“ und somit finden kann. Außerdem muss man im Fach Mathe Gleichungs-Aufgaben, wie andere Mathematik-Aufgaben auch, stets in einem vorgeschriebenen Zeitintervall lösen. Ein stetiges Ausprobieren von Zahlen, die eine mögliche Lösung der Gleichung sein könnten, widerspricht deshalb auch der schulischen Zielsetzung im Fach Mathematik. Aus diesem Grund muss bei Gleichungen immer ein zielgerichtetes Lösen angewandt werden, das heißt mittels eines Lösungsweges, der möglichst schnell zum richtigen Ergebnis der Gleichung führt. Indem man stetig auf einer Seite der Gleichung die Variable separiert, macht man dies – und dadurch kommt man schließlich zur Lösungsmenge der Gleichung.
Das schrittweise Lösen einer Gleichung bzw. das Separieren der Variablen geht hierbei vielfach über sogenannte Äquivalenzumformungen.
Äquivalenzumformungen sind hierbei immer Rechenoperationen, die mit den Grundrechenarten „+“, „–“, „·“ und „:“ an Gleichungen durchgeführt werden und mit denen man stets Schritt für Schritt näher zur Lösung der Gleichung gelangt. Denn durch zielgerichtete Äquivalenzumformungen wird eine Gleichung immer schrittweise vereinfacht.
Definition von Äquivalenzumformungen
Gleichungen nennt man zueinander äquivalent, wenn diese Gleichungen jeweils die gleiche Lösungsmenge vorweisen.
Die sogenannte Additions- und Subtraktionsregel bei Gleichungen
Addiert oder subtrahiert man auf den beiden Seiten einer Gleichung jeweils dieselbe Zahl, dann bleibt die Lösungsmenge hierdurch unverändert. Man sagt die Gleichungen sind äquivalent zueinander.
Die sogenannte Multiplikations- und Divisionsregel bei Gleichungen
Multipliziert man beide Seiten einer Gleichung jeweils mit derselben Zahl oder dividiert man beide Seiten einer Gleichung jeweils durch dieselbe Zahl (die Zahl muss hierbei immer ungleich null sein!), dann bleibt die Lösungsmenge dadurch unverändert. Man sagt die Gleichungen sind äquivalent zueinander.
Bei einer Multiplikation auf beiden Seiten der Gleichung darf niemals als Faktor die Zahl Null verwendet werden, da es sich hierbei um keine Äquivalenzumformung handelt.
Die Multiplikation und Division darf sich bei Gleichungen immer nur auf die „nackte“ Zahl vor den Variablen und anderen vorkommenden „reinen“ Zahlen beziehen. Multipliziert man eine Gleichung mit einer Variablen durch oder dividiert man bei einer Gleichung durch eine Variable beziehungsweise kürzt man hierbei eine Variable heraus, so handelt es sich nicht mehr um eine Äquivalenzumformung. Ebenso darf man Gleichungen nicht mit der Zahl Null durchmultiplizieren, da dann alle Gleichungen das gleiche, verfälschte Ergebnis liefern, nämlich unendlich viele Lösungen. Ein Teilen durch Null – wie man bereits seit dem Erlernen der Grundrechenart Division weiß – ist ebenfalls nicht erlaubt.
Anhand einer ausgewogenen Wippe, an deren beiden Enden zwei gleichgroße Boxen stehen, kann anschaulich erklärt werden, was eine Äquivalenzumformung bei Gleichungen genau ist.
Wir nehmen nun hierbei Folgendes an: In der linken Box der Wippe befinden sich 8 gleichschwere Gewichte, die jeweils 1 kg wiegen, und jeweils 10 gleichschwere Dosen, deren Gewicht unbekannt ist. In der rechten Box der Wippe liegen hingegen 10 gleichschwere Gewichte, die jeweils 1 kg wiegen, und jeweils 4 gleichschwere Dosen, deren Gewicht unbekannt ist. Das vorhandene „ausgewogene“ Gleichgewicht auf der Wippe lässt sich nun mittels dieser Gleichung wiedergeben:
8 + 10x = 10 + 4x.
Das x bei dieser Gleichung ist hier das unbekannte Gewicht der Dosen – und das kann man nun ganz einfach durch Äquivalenzumformen ermitteln.
Wie oben bereits erwähnt, sind Äquivalenzumformungen Rechenoperationen, die mit den Grundrechenarten „+“, „–“, „·“ und „:“ an jeglichen Gleichungen durchgeführt werden können, um sich Schritt für Schritt der Lösung einer Gleichung zu nähern. Bei der Gleichung 8 + 10x = 10 + 4x wird nun exemplarisch aufgezeigt werden, wie Äquivalenzumformungen an Gleichungen korrekt angewendet werden.
Um nun genau zu wissen, welche Äquivalenzumformungen bei einer Gleichung jeweils sinnvoll sind und somit schnellstmöglich zielgerichtet hin zur Lösung führen, muss man sich immer vor Augen führen, wie eine zu lösende Gleichung genau aufgebaut ist.
Wie man an der Gleichung 8 + 10x = 10 + 4x sehen kann, setzt diese sich jeweils rechts und links des Gleichheitszeichens aus zwei Einzeltermen zusammen, die stets mit einem Plus miteinander verbunden sind. Die beiden Einzelterme rechts und links des Gleichheitszeichens bestehen hierbei jeweils aus einer „nackten“ Zahl und einer mit einer Variablen verbundenen Zahl. Jetzt gilt bei dem zielgerichteten Lösen einer Gleichung Folgendes:
Jeweils davon abhängig, nach welchen Rechenzeichen sich die gleichartigen Einzelterme einer Gleichung zusammensetzen, werden die Äquivalenzumformungen durchgeführt – und das stets mittels der umgekehrten Rechenoperation. Konkret heißt das: Bei „+“ werden „–“-Äquivalenzumformungen und bei „–“„+“-Äquivalenzumformungen durchgeführt. Ebenso werden bei „·“ „:“-Äquivalenzumformungen und bei „:“„·“-Äquivalenzumformungen gemacht. Und weil die getätigten Rechenoperationen jeweils Äquivalenzumformungen sein sollen, müssen diese jeweils gleichermaßen rechts und links des Gleichheitszeichen durchgeführt werden. Die getätigte Rechenoperation wird hierbei stets zusätzlich an der rechten Seite der Gleichung hingeschrieben, abgetrennt durch das Operatorzeichen |.
Darüber hinaus müssen natürlich die zielgerichteten Äquivalenzumformungen immer dahin gehen, dass am Ende auf einer Seite der Gleichung nur die unbekannte Variable steht und auf der anderen Seite der Gleichung eine „nackte“ Zahl. Das nennt man das Separieren der Variablen – und nur dadurch erhält man ein absolut eindeutiges Ergebnis.
Wir lösen nun die Gleichung 8 + 10x = 10 + 4x Schritt für Schritt über Äquivalenzumformungen:
Zuerst eliminieren wir hier die „nackte“ Zahl 8, indem die Äquivalenzumformung „– 8“ durchgeführt wird.
8 (–8) + 10x = 10 (–8) + 4x | – 8 <=>
0 + 10x = 2 + 4x <=>
10x = 2 + 4x
Darauf eliminieren wir das „4x“, indem wir die Äquivalenzumformung „– 4x“ machen.
10x (–4x) = 2 + 4x (–4x) | – 4x <=>
6x = 2
Zum Schluss eliminieren wir den Faktor 6, indem wir die Äquivalenzumformung „:6“machen.
6x : 6 = 2 : 6 | : 6 <=>
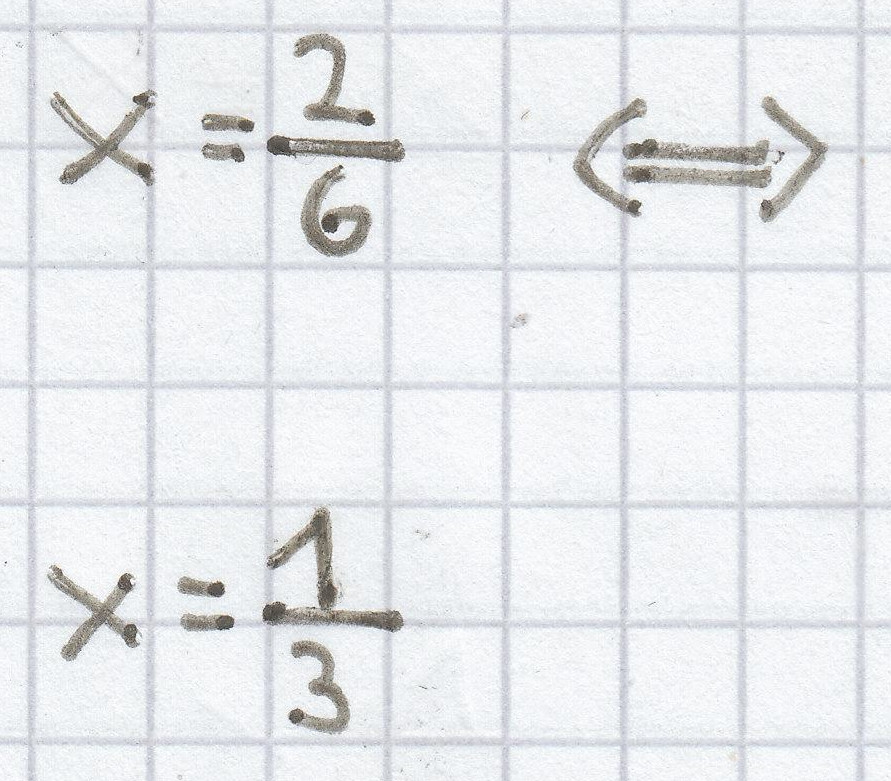
Die Lösung der Gleichung ist demzufolge
L =

.
Hinsichtlich des „ausgewogenen“ Gewichts bei der Wippe kann jetzt genau gesagt werden, dass rechts und links in den Boxen die Dosen jeweils
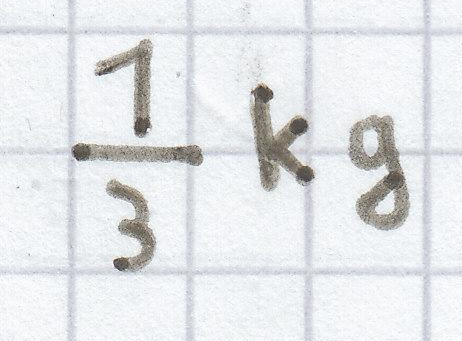
wiegen und dass das Gesamtgewicht rechts und links der Boxen schließlich,
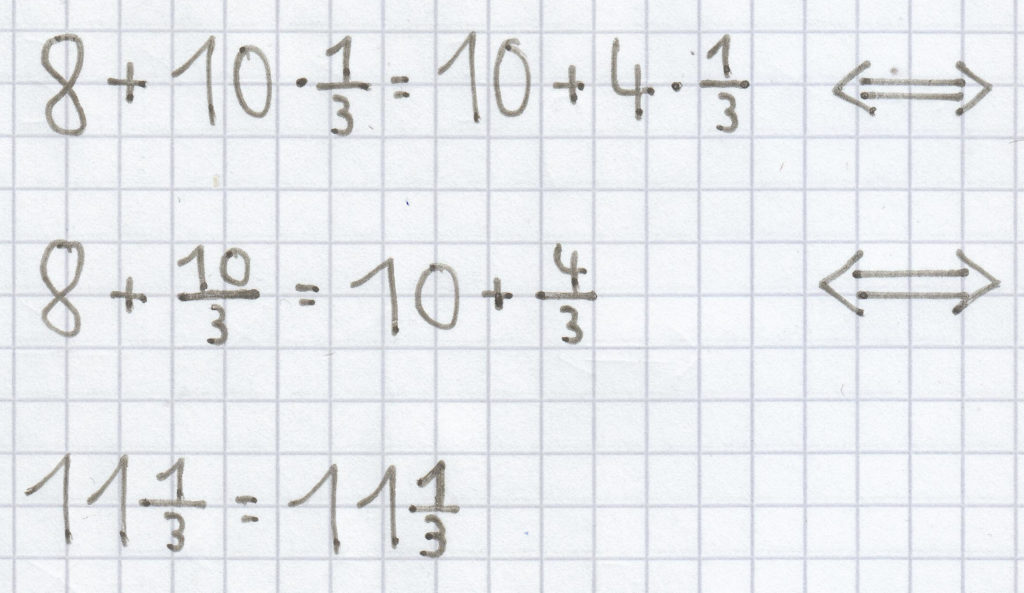
, jeweils
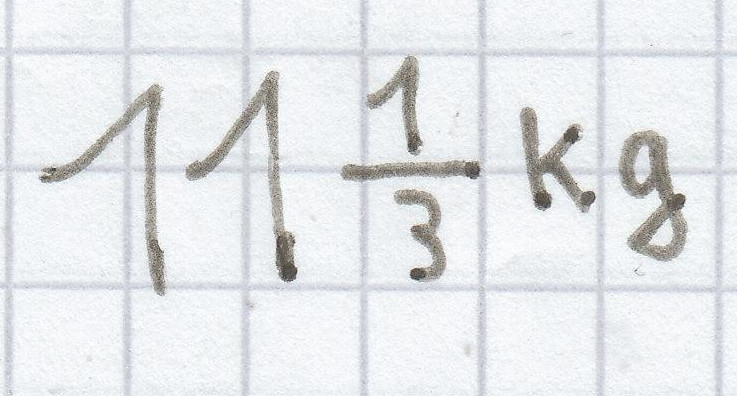
ist.
3.1 Die Probe an der Gleichung
Die Lösung in die Ursprungsgleichung einzusetzen, nennt man die Probe. Nur wenn dann „rechts“ und „links“ der Gleichung das gleiche Ergebnis herauskommt, bestätigt die Probe die Richtigkeit der Ergebnisses. Ist das nicht der Fall, so ist der Ergebnis keine Lösung der Gleichung.
Obige Lösung
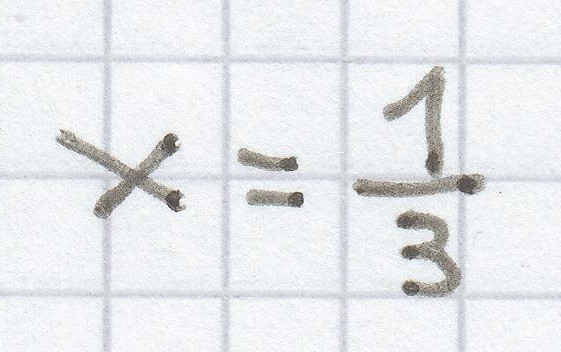
würde dann mittels Probe noch einmal korrekt in der Ursprungsgleichung eingesetzt so aussehen:
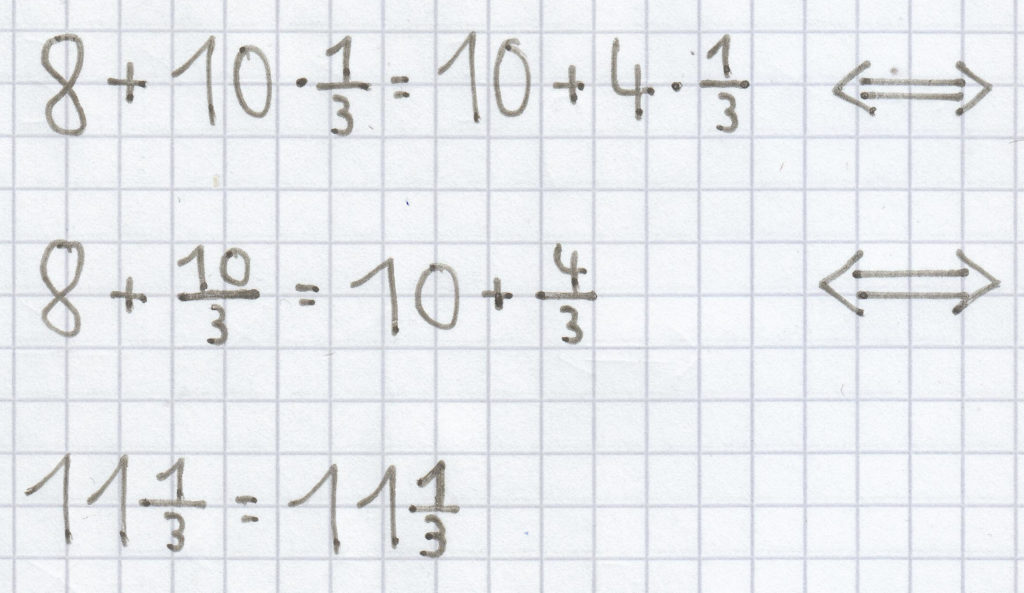
Die Probe bestätigt die Richtigkeit des Ergebnisses.
Wäre bei der Probe nicht eine wahre Aussage entstanden, so hätte es sich nicht um eine Lösung der Gleichung gehandelt.
3.2. Übliche Schreibweise von Äquivalenzumformungen in der Schule
In der Schule werden normalerweise die Äquivalenzumformungen jeglicher Gleichungen nur verkürzt wiedergegeben. Man sagt hierbei oftmals auch bei Plus- und Minus-Äquivalenzumformungen, damit die Schüler sich die zielführenden Lösungsschritte besser einprägen können, „es wird der eine Term auf die andere Seite gebracht“ – was zwar aus Mathe-Sicht nicht wirklich zu 100 % korrekt ist. Innerhalb der auf dem Blatt stehenden Lösungsschritte – wo ja keinerlei Phonetik mehr zu höhren ist – ist der zielführende Lösungsweg deshalb aber trotzdem dann richtig. Und das ist aus der Mathematik-Sicht das alles Entscheidende.
Nachfolgend wird anhand der gleichen Gleichung gezeigt, wie verkürzte, in der Schule übliche Äquivalenzumformungen aussehen.
8 + 10x = 10 + 4x | – 8 <=>
(hier sagt man, man bringt das „– 8″ auf die andere Seite der Gleichung. Gleichzeitig lässt man dann bei der darauf sich ergebenden Gleichung auf der einen Seite das „+ 8″ weg.
10x = 10 (–8) + 4x <=>
10x = 2 + 4x | – 4x <=>
(hier sagt man, man bringt das „– 4x“ auf die andere Seite der Gleichung. Gleichzeitig lässt man dann bei der sich daraus ergebende Gleichung wiederum auf der einen Seite das „+ 4x“ weg.
10x (–4x) = 2 <=>
6x = 2 | : 6 <=>
(bei der Division ist in der Schule ebenfalls eine verkürzte Schreibweise üblich. Diese Rechenoperation wird aber nicht mehr mit einer bestimmten eigenen Aussage gelernt. Man lässt einfach bei der sich daraus ergebenden Gleichung erneut auf der einen Seite der Gleichung das „·“, hier in diesem Beispiel das „· 6“, weg. Auf die gleiche Weise verhält es sich bei Rechenoperationen mit der Grundrechenart Multiplikation.
x = 2 : 6 <=>
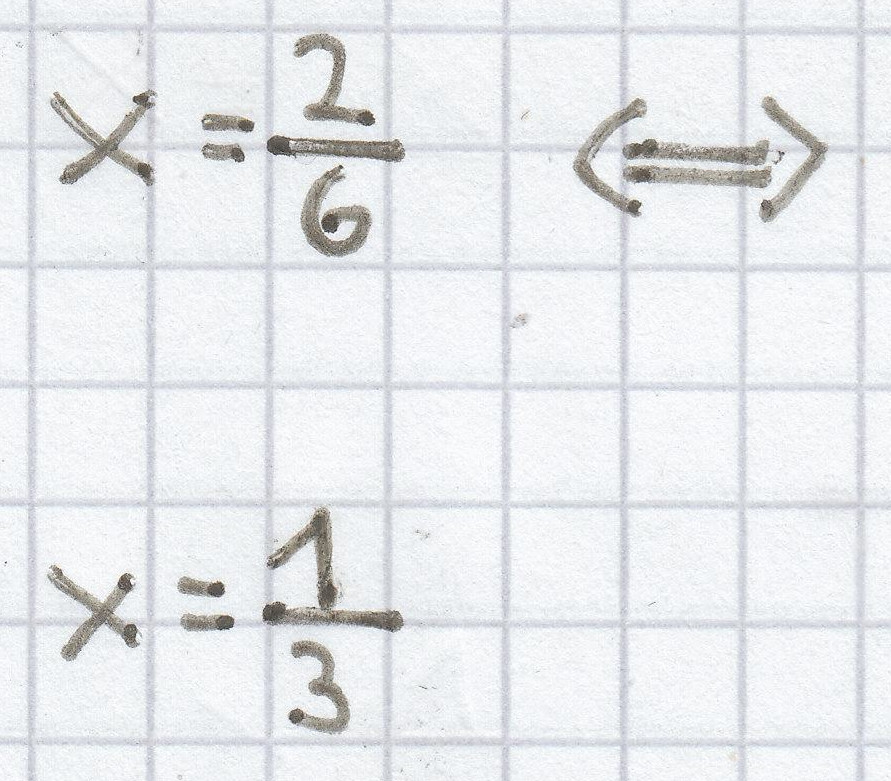
Jede Gleichung kann man auch immer um gewissermaßen 180º drehen. Hierbei handelt es sich auch um eine Äquivalenzumformung.
Beispiel:
8 + 10x = 10 + 4x <=> 10 + 4x = 8 + 10x