
1. Allgemeines zu den binomischen Formeln
Eine sehr wichtige Sonderform beim Auflösen zweier Term-Klammern mittels des Distributivgesetzes (auch Verteilungsgesetz genannt) stellen die binomischen Formeln dar. Zum einen kann man hierdurch nämlich viel schneller und fehlerfreier solche Term-Klammern auflösen, zum anderen muss man oft die binomischen Formeln beim quadratischen Ergänzen von quadratischen Gleichungen und Funktionen anwenden (entweder zur Nullstellen- oder Scheitelpunkt-Bestimmung). Des Weiteren kommen auch noch in der Oberstufe bei der Analysis/Kurvendiskussion immer wieder quadratische Funktionen und Gleichungen vor – und somit auch die binomischen Formeln. Daher sind die binomischen Formeln eine algebraische Gesetzmäßigkeit, die man unbedingt beherrschen muss – ansonsten wird man ab der 8. Klasse mehr und mehr keinen Durchblick mehr in Mathe haben. Schließlich muss man in den weiteren Klassenstufen ebenso weitere Algebra-Kenntnisse aus dem Effeff können. Nur so ist gewährleistet, dass man überhaupt die Aufgabe versteht – und somit den richtigen Lösungsweg findet. Eine möglichst fehlerfreie und schnelle Berechnung des Ergebnisses ist dann nur noch die Kür, die man aber trotzdem stets problemlos abrufen können sollte. Hat man da aber noch Probleme mit den binomischen Formeln und versteht eher nur Bahnhof, ist auf jeden Fall im Fach Mathematik „Land unter“ angesagt. Und dann hat man wirklich ein ernsthaftes Problem in Mathematik, da ja der Lernstoff trotzdem weitergeht… Für viele Schülerinnen und Schüler ist dann oftmals der Zug in diesem Fach fast bereits abgefahren – und demzufolge nahezu uneinholbar! Deshalb sollte man die binomischen Formeln sehr gut können – und das auswendig, so dass es erst überhaupt nicht so weit kommt. Durch üben, üben und nochmals üben wird das aber auch ohne Weiteres klappen!
Es gibt drei binomische Formeln, die jeweils auf zwei verschiedene Arten dargestellt werden. Entweder in der unaufgelösten Form mit Klammer oder in der aufgelösten Form ohne Klammer. Beide Arten sollte man bei allen drei binomischen Formeln „im Schlaf“ vorsagen können.
1. Binomische Formel: (a + b)² = a² + 2ab + b²
2. Binomische Formel: (a – b)² = a² – 2ab + b²
3. Binomische Formel: (a + b) · (a – b) = a² – b²
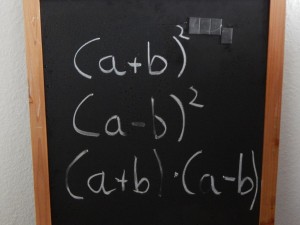
2. Erklärung der 1. Binomischen Formel
(a + b)² = (a + b) · (a + b) =
a · a + a · b + b · a + b · b = a² + ab + ab + b² =
a² + 2ab + b²
Beim Auflösen der beiden Klammern mittels Ausmultiplizieren und Anwendung des Distributivgesetztes/Verteilungsgesetzes ergeben sich zunächst immer vier Einzelterme. Hierbei ist es völlig egal, wie man mit dem Ausmultiplizieren beginnt.
Das Besondere beim Ausmultiplizieren der 1. Binomischen Formel ist nun, dass zwei/„ab + ab = 2ab“ der vier Einzelterme identisch sind – und somit addiert/zusammengefasst werden können. Dadurch entsteht die aus drei Einzeltermen bestehende aufgelöste Form der 1. Binomischen Formel – woraus eine Regelmäßigkeit ableitbar ist. Der Anfangsterm/„a²“ und der Endterm/„b²“ ergeben sich immer aus den beiden in der Klammer stehenden Einzelterme/„(a + b)²“ und stehen immer im Quadrat. Der Mittelterm/„2ab“ ergibt sich immer aus dem zweifachen Produkt der beiden in der Klammer stehenden Einzeltermen/„(a + b)²“.
Beispiele zur 1. Binomischen Formel
1. (m + n)² = (m)² + 2 · m · n + (n)² = m² + 2mn + n²
2. (3s + t)² = (3s)² + 2 · 3s · t + (t)² = 9s² + 6s + t²
3. (a + 5b)² = (a)² + 2 · a · 5b + (5b)² = a² + 10ab + 25b²
4. (12a + 8b)² = (12a)² + 2 · 12a · 8b + (8b)² = 144a² + 192ab + 64b²
In der Klammer einer binomischen Formel können auch ganze Zahlen, Bruchzahlen und Dezimalzahlen auftreten. Das gilt für alle drei binomischen Formeln.
5. (9 + a)² = (9)² + 2 · 9 · a + (a)² = 81 + 18a + a² = a² + 18a + 81
6.
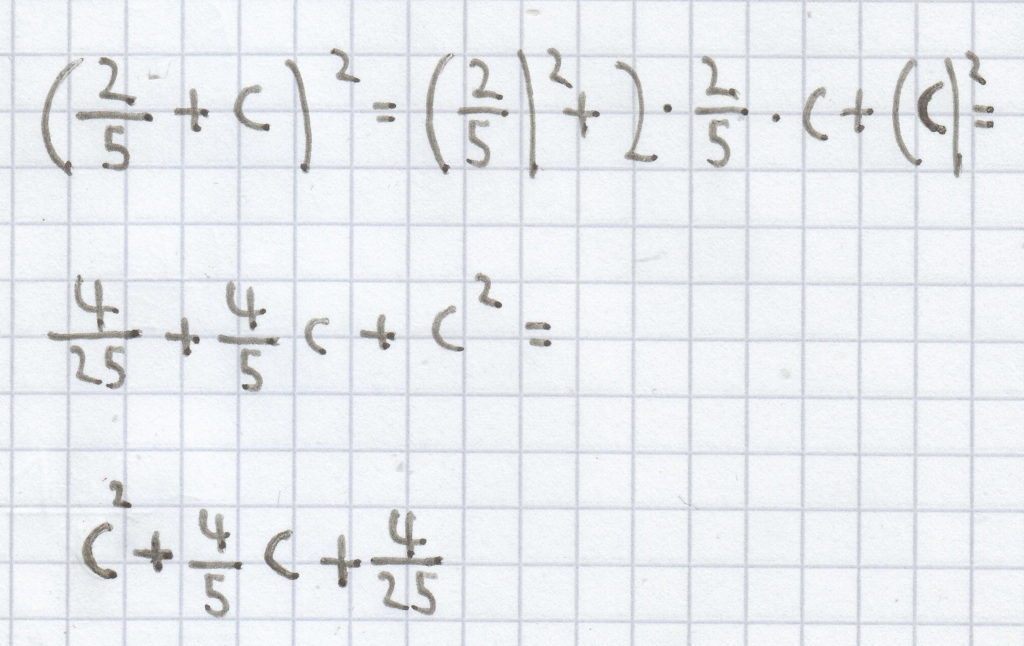
7. (3,5 + 8b)² = (3,5)² + 2 · 3,5 · 8b + (8b)² = 12,25 + 56b + 64b² = 64b² + 56b + 12,25
Bei jeder binomischen Formel gilt darüber hinaus das Kommutativgesetz/Vertauschungsgesetz. Daher können die vorkommenden Variablen und Zahlen in der Klammer jeweils vertauscht werden.
8. (15b + 9a)² = (9a + 15b)² = 81a² + 270ab + 225b²
9. (7 + b)² = (b + 7)² = b² + 14b + 49
3. Erklärung der 2. Binomischen Formel
(a – b)² = (a – b) · (a – b) =
a · a + a · (–b) + (–b) · a + (–b) · (–b) =
a² + a · (–b) + a · (–b) + b² = a² – 2ab + b²
Die 2. Binomische Formel unterscheidet sich zur 1. Binomischen Formel nur dahingehend, dass in der aufgelösten Form der Mittelterm anstatt eines positiven („+“) ein negatives („–“) Vorzeichen hat. Das liegt an dem in der 2. Binomischen Formel auftretenden Minuszeichen in der unaufgelösten Form. Multipliziert man nämlich die Klammern mittels des Distributivgesetzes/Verteilungsgesetzes aus, so tritt wieder der Sonderfall wie bei der 1. Binomischen Formel auf, und zwar, dass zwei/„(–ab) + (–ab) = –2ab“ der vier Einzelterme identisch sind und deshalb wiederum addiert/zusammengefasst werden können. Aufgrund des Minuszeichens in der Klammer weist der Mittelterm aber ein negatives Vorzeichen auf. Hierdurch ensteht schließlich die aus drei Einzeltermen bestehende aufgelöste Form der 2. Binomischen Formel – woraus wiederum eine Regelmäßigkeit ableitbar ist. Wie bei der 1. Binomischen Formel ergeben sich bei der 2. Binomischen Formel der Anfangsterm/„a²“ und der Endterm/„b²“ aus den beiden in den Klammern stehenden Einzeltermen/„(a – b)²“, wobei beide immer im Quadrat stehen. Der Mittelterm setzt sich immer aus dem zweifachen Produkt der beiden in der Klammer stehenden Einzelterme/„(a – b)²“ zusammen, wobei das Vorzeichen des Mittelterms immer ein Minuszeichen/„–“ ist.
Beispiele zur 2. Binomischen Formel
1. (f – g)² = (f)² – 2 · f · g + (g)² = f²– 2fg + g²
2. (4c – d) = (4c)² – 2 · 4c · d + (g)² = 16c² – 8cd + d²
3. (a – 7b)² = (a)² – 2 · a · 7b + (7b)² = a² – 14ab + 49b²
4. (12a – 15b)² = (12a)² – 2 · 12a · 15b + (15b)² = 144a² – 360ab + 225b²
Beachte, dass aufgrund des Kommutativgesetzes/Vertauschungsgesetzes auch diese Beispiele unter die 2. Binomische Formel fallen.
5. (–12b + 3a)² = (3a –12b)² = 9a² – 72ab + 144b²
6. (–9 + 18c)² = (18c – 9)² = 324c² – 324c + 81
4. Erklärung der 3. Binomischen Formel
(a + b) · (a – b) = a · a + a · (– b) + b · a + b · (– b) =
a² – ab + ab – b² = a² – b²
Die 3. Binomische Formel unterscheidet sich zur 1. und zur 2. Binomischen Formel auf zweifache Weise. Zum einen besteht diese in der unaufgelösten Form aus zwei Klammern, deren darin enthaltene Einzelterme nicht wie bei der 1. und 2. Binomischen Formel doppelt vorkommen. Zum anderen hat die 3. Binomische Formel in der aufgelösten Form keinen Mittelterm und besteht daher nur aus zwei Einzeltermen. Dadurch, dass bei der 3. Binomischen Formel nun nicht wie bei der 1. und 2. Binomischen Formel zwei Klammern mit identischen Einzeltermen mittels des Distributivgesetzes/Verteilungsgesetzes ausmultipliziert werden, sondern zwei Klammern, die sich bei dem zweiten Einzelterm nur durch das Vorzeichen unterscheiden („+“, „–“) ergibt sich ein weiterer Sonderfall. Denn hierdurch eliminiert sich der Mittelterm/„– ab + ab = 0“ und man erhält die nur aus zwei Einzeltermen bestehende aufgelöste Form – woraus sicher erneut eine Regelmäßigkeit ableiten lässt. Der Anfgangsterm/„a²“ und der Endterm/„b²“ der 3. Binomischen Formel ergeben sich immer aus den beiden ersten mit sich malgenommen Termen (a + b) · (a – b) und den beiden letzten miteinander malgenommenen Termen (a + b) · (a – b), wobei das verbindende Vorzeichen beider Einzelterme/„a² – b²“ immer ein Minuszeichen/„–“ ist.
Beispiele zur 3. Binomischen Formel
1. (k + l) · (k – l) = (k)² – (l)² = k² – l²
2. (3r + s) · (3r + s) = (3r)² – (s)² = 9r² – s²
3. (a + 9b) · (a – 9b) = (a)² – (9b)² = a² – 81b²
4. (18a + 14b) · (18a – 14b) = (18a)² – (14b)² = 324a² – 196b²
Beachte auch bei der 3. Binomischen Formel, dass hier das Kommutativgesetz/Vertauschungsgesetz gilt, und das nicht nur bei den Variablen und Zahlen innerhalb der Klammern, sondern auch bei den Klammern selbst. Denn es handelt sich hier um Klammern, die durch ein Mal-Zeichen miteinander verbunden sind, weswegen auch hier das Kommutativgesetz/Vertauschungsgesetz angewendet werden darf.
5. (s + t) · (–t + s) = (s + t) · (s – t) = s² – t²
6. (–12b + 2a) · (2a + 12b) = (2a – 12b) · (2a + 12b) = (2a + 12b) · (2a –12b) = 4a² – 144b²