1. Allgemeines zum Einsetzungsverfahren
Bei diesem Lösungsverfahren eines linearen Gleichungssystems (LGS) steht das Einsetzen einer Gleichung in die andere Gleichung im Mittelpunkt.
Zum Lösen eines LGS mittels des Einsetzungsverfahrens, kann man drei verschiedene Wege heranziehen.
a) Man löst das LGS nach der Variablen x hin auf.
b) Man löst das LGS nach der Variablen y hin auf.
c) Man löst das LGS nach einer gemeinsamen Variablen mit einem gemeinsamen Faktor hin auf.
2. Erster Lösungsweg mittels des Einsetzungsverfahrens
Der erste Lösungswege beinhaltet eine Gleichung nach der Variablen x hin aufzulösen. Diese derart aufgelöste Gleichung wird dann in die andere Ursprungsgleichung eingesetzt.
I. 3x – 2y = –2
II. 6x – 5y = –8
Zuerst wird die Variable x einer Gleichung separiert.
I. 3x – 2y = – 2 | + 2y
II. 6x – 5y = – 8
I. 3x = –2 + 2y | : 3
II. 6x – 5y = –8
I.
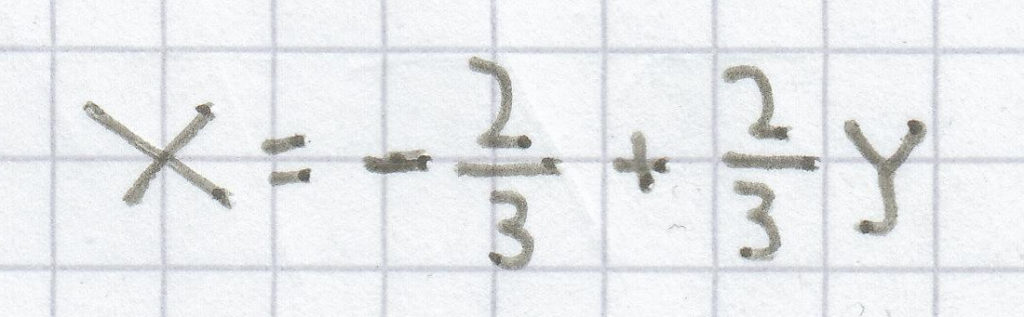
II. 6x – 5y = –8
Darauf setzt man die nach x hin aufgelöste Gleichung in die andere Gleichung ein.
I. in II.
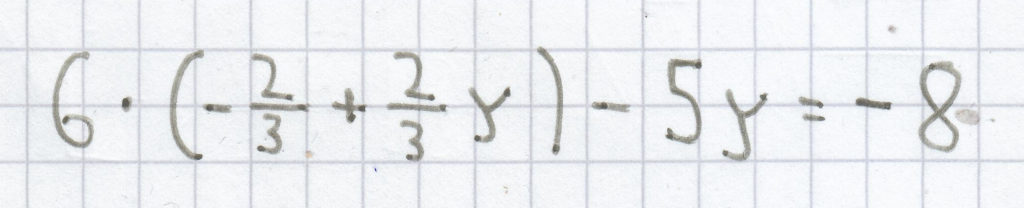
Diese Gleichung löst man nun nach der Variablen y hin auf.
I. in II.
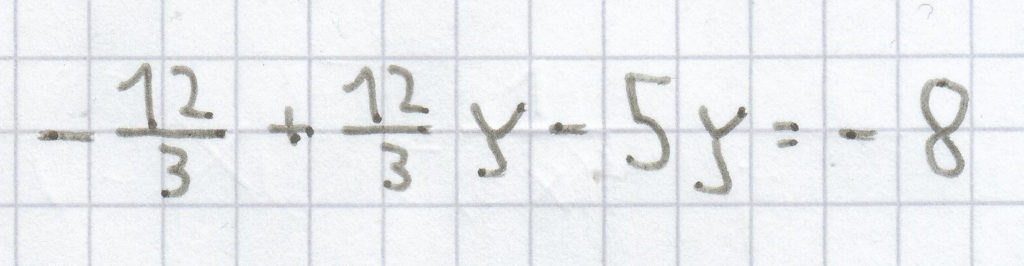
I. in II. –4 + 4y – 5y = –8
I. in II. –4 – y = –8 | + 4
I. in II. –y = –4 | · (–1)
I. in II. y = 4
Die erste Lösungskoordinate setzt man in eine der beiden Ursprungsgleichungen ein.
I. 3x – 2 · 4 = –2
Diese Gleichung löst man dann nach der Variablen x hin auf.
I. 3x – 8 = –2 | + 8
I. 3x = 6 | : 3
I. x = 2
Die Probe bestätigt die Lösung des LGS.
I. 3 · 2 – 2 · 4 = –2
II. 6 · 2 – 5 · 4 = –8
I. 6 – 8 = –2
II. 12 – 20 = –8
I. –2 = –2
II. –8 = –8
Die Lösungsmenge des LGS.
L = {2 | 4}
3. Zweiter Lösungsweg mittels des Einsetzungsverfahrens
Der zweite Lösungsweg zielt darauf, eine der beiden Gleichungen nach der Variablen y hin aufzulösen. Diese so aufgelöste Gleichung wird dann in die andere Ursprungsgleichung eingesetzt.
I. 3x – 2y = –2
II. 6x – 5y = –8
Als Erstes wird eine Gleichung nach der Variablen y hin aufgelöst.
I. 3x – 2y = –2 | – 3x
II. 6x – 5y = –8
I. –2y = –2 – 3x | : (–2)
II. 6x – 5y = –8
I. y = 1 + 1,5x
II. 6x – 5y = –8
Darauf setzt man die nach y hin aufgelöste Gleichung in die andere Gleichung ein.
I. in II. 6x – 5 · (1 + 1,5x) = –8
Diese Gleichung löst man nach der Variablen x hin auf.
I. in II. 6x – 5 – 7,5 x = –8
I. in II. –1,5x – 5 = –8 | + 5
I. in II. –1,5x = –3 | : (–1,5)
I. in II. x = 2
Die eine Lösungskoordinate setzt man in eine der beiden Ursprungsgleichungen ein.
I. 3 · 2 – 2y = –2
I. 6 – 2y = –2
Diese Gleichung löst man dann nach der Variablen x hin auf.
I. 6 – 2y = –2 | – 6
I. –2y = –8 | : (–2)
I. y = 4
Die Probe bestätigt die Richtigkeit der beiden Lösungskoordinaten.
I. 3 · 2 – 2 · 4 = –2
II. 6 · 2 – 5 · 4 = –8
I. 6 – 8 = –2
II. 12 – 20 = –8
I. –2 = –2
II. –8 = –8
Die Lösungsmenge des LGS.
L = {2 | 4}
4. Dritter Lösungsweg mittels des Einsetzungsverfahrens
Der drittel Lösungsweg beinhaltet, eine Gleichung nach einer Variabel mit Faktor hin umzuformen (wie 2x oder 4y), die ebenfalls in der gleichen Form in der anderen Gleichung vorkommt.
I. 3x – 2y = –2 | · 2
II. 6x – 5y = –8
Hier kann man die erste Gleichung mit dem Faktor 2 malnehmen. Dadurch erzeugt man die Variable x mit einem Faktor, die genau der Variable x mit Faktor in der zweiten Gleichung entspricht.
I. 6x – 4y = –4 | + 4y
II. 6x – 5y = –8
Darauf separiert man die erste Gleichung nach 6x hin.
I. 6x = –4 + 4y
II. 6x – 5y = –8
Jetzt setzt man die erste Gleichung in die zweite Gleichung ein.
I. in II. –4 + 4y – 5y = –8
I. in II. –4 – y = –8 | + 4
I. in II. –y = –4 | · (–1)
I. in II. y = 4
Die erste Lösungskoordinate setzt man in eine der beiden Urspungsgleichungen ein.
I. 3x – 2 · 4 = –2
I. 3x – 8 = –2 | + 8
I. 3x = 6 | : 3
I. x = 2
L = {2 | 4}
Die Probe bestätigt, dass die Lösungsmenge korrekt ist.
I. 3 · 2 – 2 · 4 = –2
II. 6 · 2 – 5 · 4 = –8
I. 6 – 8 = –2
II. 12 – 20 = –8
I. –2 = –2
II. –8 = –8
5. Vorgehensweise beim Lösen eines linearen Geichungssystems mit dem Einsetzungsverfahren
Beim Lösen eines linearen Gleichungssystems mittels des Gleichsetzungsverfahrens geht mal folgendermaßen vor.
- Als Erstes löst man eine Gleichung des linearen Gleichungssystems nach der Variablen x oder y hin um oder man erzeugt eine Vielfaches von x und y (wie beispielsweise 2x oder 4y), wenn diese Variable mit Faktor ebenfalls in der zweiten Gleichung auftritt. Darauf separiert man die Variable mit Faktor.
- Darauf setzt man die nach x oder y oder einer Variablen mit Faktor aufgelösten Gleichung in die andere Gleichung ein. Hierbei kann man die andere Gleichung beibehalten oder erst nach der Ermittlung der ersten Lösungskoordinate wieder aufgreifen, wenn man diese mit römischen Ziffern versehen hat.
- Diese Gleichung, die nun nur noch eine Variable vorweist, löst man nach der Variablen hin auf. Die separierte Variable stellt eine Lösungskoordinate des LGS dar.
- Die Lösungskoodinate setzt man in eine der beiden Ursprungsgleichungen ein und löst die Gleichung nach der Variablen hin auf. Die separierte Variable ergibt die zweite Lösungskoordinate.
- Die Probe bestätigt die Lösung des LGS.
- Die Lösungskoordinaten ergeben die Lösungsmenge des linearen Gleichungssystems