
Gerade bei Vielecken und ebenso bei zweidimensionalen Figuren müssen Schülerinnen und Schüler häufig deren Umfang ermitteln. Das sollte eigentlich nicht so schwierig sein (aber ein Selbstläufer ist es auch nicht 😉 )! Die „Wegstrecke“, die man gedanklich bei einem Vieleck oder irgendeiner anderen Figur herumgehen kann, stellt deren Umfang dar. Daher besteht der Umfang auch aus verschiedenen Teilstrecken/Randstrecken, die man allesamt addiert. Normalerweise kommt hierbei eine zweite Berechnungsweise von Vielecken und anderen ebenso zweidimensionalen Figuren zum Zuge, deren Flächeninhalt, da der Umfang häufig mit diesem in Beziehung gesetzt wird.
Aufgaben zum Umfang und Flächeninhalt von Vielecken
1. Ein Rechteck hat eine Länge von 9 m und besitzt einen Umfang von 86 m. Wie groß ist seine Breite? Folgende Ergebnisse wurden von verschiedenen Schülerinnen und Schülern ermittelt.
(1) b = 90 m; (2) b = 77 m; (3) = 18 m2; (4) = 34 m.
a) Lege dar, warum drei Ergebnisse augenscheinlich falsch sein müssen.
b) Berechne die Breite des Rechtecks?
2. Ein Rechteck besitzt einen Umfang von 72 cm. Eine Länge des Rechtecks ist doppelt so groß wie eine Breite des Rechtecks.
a) Berechne die Seitenlängen des Rechtecks.
b) Berechne den Flächeninhalt des Rechtecks.
3. Ein Quadrat hat die Seitenlänge 12,5 cm.
a) Berechne den Umfang des Quadrats.
b) Beschreibe, wie man den Umfang eines Quadrats berechnet.
c) Nenne eine allgemeine Formel zur Berechnung eines Quadrats mit der Seitenlänge a.

Lösungen
1. Ein Rechteck hat eine Länge von 9 m und besitzt einen Umfang von 86 m. Wie groß ist seine Breite? Folgende Ergebnisse wurden von verschiedenen Schülerinnen und Schülern ermittelt.
(1) b = 90 m; (2) b = 77 m; (3) = 18 m2; (4) = 34 m.
a) Lege dar, warum drei Ergebnisse augenscheinlich falsch sein müssen.
Wenn man weiß, dass der Umfang bei einem Rechteck sich zusammensetzt durch jeweils das Doppelte der Länge und der Breite, also sich die Summe aus zweimal der Länge und zweimal der Breite ergibt, so kann man diese Ergebnisse sofort ausschließen:
(1) b = 90 m
Denn hier ist das Ergebnis der Breite größer als der Umfang, was niemals der Fall sein kann!
(2) b = 77 m
Denn die Breite ist viel zu groß, sodass sich ein viel größerer Umfang als angegeben egeben müsste.
(3) 18 m2
Denn die Breite kann niemals die Einheit Quadratmeter vorweisen, da hier eine Länge gesucht ist und keine Fläche.
(4) = 34 m
Da die anderen Ergebnisse offensichtlich falsch sind, muss dieses aufgrund des Eliminationsprinzipes auch das richtige sein!
b) Berechne die Breite des Rechtecks?
Die Gleichung zur Berechnung des Umfangs bei einem Rechteck ist folgende:
UR = 2a + 2b
a ist hiebei die Länge und b die Breite.
Diese Gleichung formt man nun algebraisch nach der Variablen b hin um.
UR = 2a + 2b | – 2a
UR – 2a = 2b | : 2
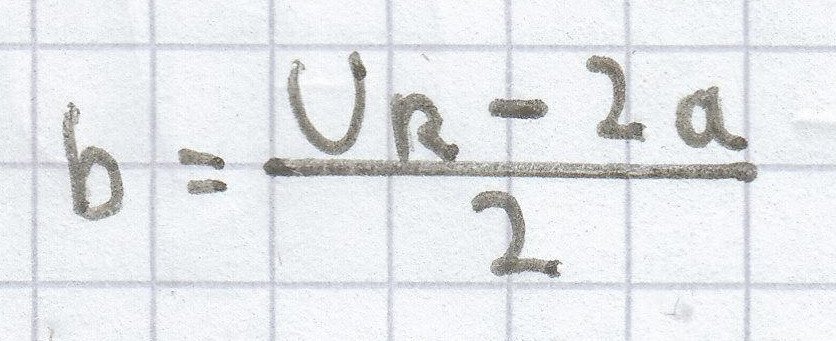
Jetzt setzt man den Umfang 86 m und die Länge 9 m in diese nach der Breite hin aufgelöste Gleichung ein.
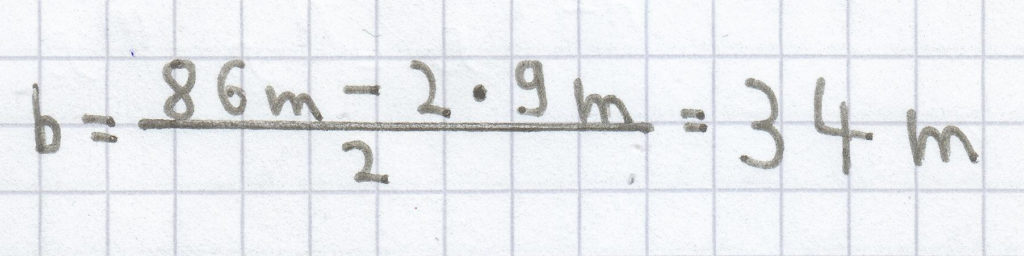
Die Breite des Rechtecks ist 34 m.
2. Ein Rechteck besitzt einen Umfang von 72 cm. Eine Länge des Rechtecks ist doppelt so groß wie eine Breite des Rechtecks.
a) Berechne die Seitenlängen des Rechtecks.
Die Gleichung zur Berechnung des Umfangs bei einem Rechteck ist diese:
UR = 2a + 2b (1)
Es gilt nun:
a = 2b (also die Länge, eine Seite, ist doppelt so groß wie die Breite, die andere Seite) (2)
Die zweite Gleichung setzt man nun in die erste Gleichung ein und löst diese nach der Variablen b hin auf.
(2) in (1)
UR = 2 · 2b + 2b
UR = 4b + 2b
UR = 6b | : 6
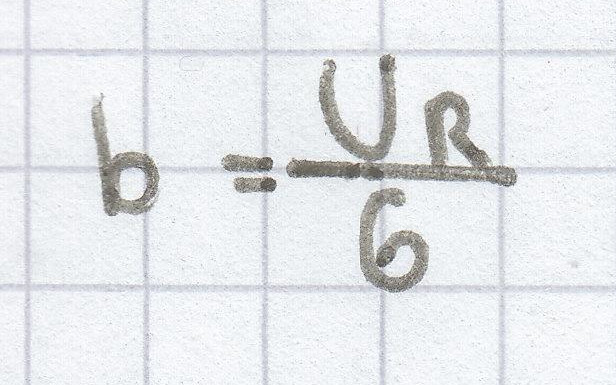
Jetzt setzt man den Umfang von 72 cm in die Gleichung ein.
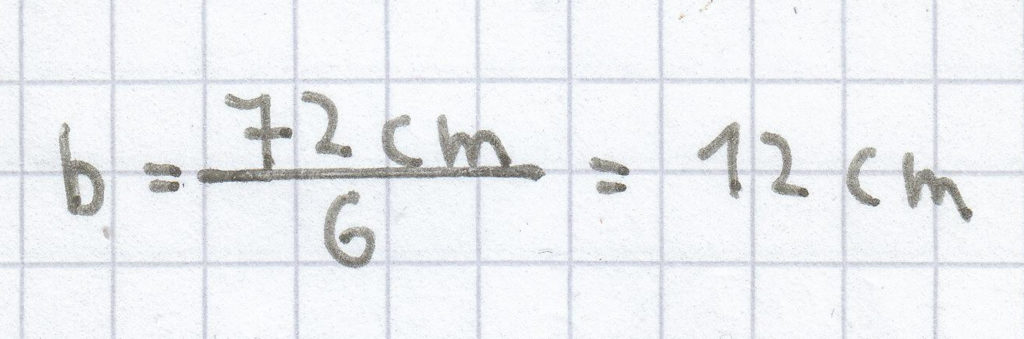
Die Breite des Dreiecks beträg 12 cm.
Nun kann man die Länge des Rechtecks berechnen.
a = 2b
a = 2 · 12 cm
a = 24 cm
Die Länge des Rechtecks beträgt 24 cm.
b) Berechne den Flächeninhalt des Rechtecks.
Den Flächeninhalt des Rechtecks berechnet man wie folgt:
AR = a · b
Die Länge 24 cm und die Breite 12 cm setzt man nun in die Gleichung ein.
AR = 24 cm · 12 cm
AR = 288 cm2
Der Flächeninhalt des Rechtecks beträgt 288 cm2.
3. Ein Quadrat hat die Seitenlänge 12,5 cm.
a) Berechne den Umfang des Quadrats.
Ein Quadrat besitzt 4 gleichlange Seiten, diese summiert man zum Umfang hin. Daher ergibt sich folgender Umfang.
UQ = 12,5 cm + 12,5 cm + 12,5 cm + 12,5 cm
UQ = 50 cm
Der Umfang des Quadrats beträgt 50 cm.
b) Beschreibe, wie man den Umfang eines Quadrats berechnet.
Wie oben schon dargelegt, besitzt ein Quadrat 4 gleichlange Seiten, die man zur Berechnung dessen Umfangs addiert.
c) Nenne eine allgemeine Formel zur Berechnung eines Quadrats mit der Seitenlänge a.
Da man eine Seitenlänge des Quadrats mit der Variablen a versehen kann, setzt sich der Umfang eines Quadrats folgendermaßen zusammen:
UQ = a + a + a + a = 4a.