
In der Mathematik kann man immer ganz eindeutig sagen, ob beispielsweise zwei Zahlen, zwei Terme, zwei Funktionen oder gar zwei Gleichungen gleich sind. Ist im Fach Mathe nämlich etwas gleich einem anderen, dann ist das miteinander Verglichene immer auch identisch. In unserer alltäglichen, unmathematischen Welt sieht dies jedoch ganz anders aus – vorausgesetzt man nimmt das Wort „gleich“ wortwörtlich. Denn hier kann man oft unendliche Diskussionen entfachen, wenn ein Otto Normalverbraucher von „gleich im Sinne von identisch“ spricht und sein Gesprächspartner ein Mathematiker oder ein Philosoph ist. Ein gemeinsamer Stadt-Spaziergang kann dann auch schon mal in einer Endlosdiskussion ausarten, wenn der Otto Normalverbraucher damit anfängt, dass nach seinem Empfinden alle Menschen mehr und mehr gleich angezogen seien und gleich aussähen. Als Beispiel führt er sogleich auch zwei vor ihnen zu sehende junge Menschen an, die nach seiner Meinung nach das gleiche Outfit und die gleichen Frisuren hätten. „Früher wäre dies“, so fährt er prompt fort, „vollkommen anders gewesen, da damals nicht alle Menschen uniform ausgesehen hätten.“

Hier fühlt sich natürlich der Mathematiker oder Philosoph sofort in seiner sprachlichen Weltanschauung erschüttert. Daher hält er ihm entgegen, dass er doch nicht offensichtlich das richtig sehe, was er vor seinen Augen wahrnehme. Hierzu müsse man sich bei den beiden jungen Menschen nur einmal die Farben ihrer Kleidungsstücke und die getragene Frisur anschauen, dann sähe man sofort augenscheinlich eine große Ungleichheit. Eine blaue Hose sei nämlich nicht gleich einer grauen Hose, ein grünes T-Shirt nicht gleich einem braunen T-Shirt und ebenso sei ein weißer Schuh offensichtlich ungleich einem schwarzen. Ebenfalls könne man nicht leugnen, dass ein Mittelscheitel in keinerlei Weise einem Retro-Beatles-Look gleiche. Der Otto Normalverbraucher fühlt sich nun seitens seines Mathematiker- beziehungsweise Philosophen-Freundes missverstanden und erwidert ihm, dass er eigentlich meinte, dass beide gleich trendige Klamotten und gleich trendige Frisuren hätten und früher die Menschen überhaupt nicht „trendy-geil“ gewesen wären. Das kann nun wiederum der mathematische beziehungsweise philosophische Weggefährte so nicht einfach stehen lassen, da seiner Meinung nach abstrakte Begriffe wie beispielsweise „trendy“ gar nicht erst einen Vergleich zulassen, der auf eine Gleichheit oder Ungleichheit hinauslaufe…
Ist das nicht schön, dass in der Mathematik bei etwa Gleichungen überhaupt keine Gleichheits- oder Ungleichheitsproblematiken aufkommen?!
Aufgaben zum Mathe-Stoffgebiet: Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Bestimme bei folgenden Gleichungen die Lösung, ohne eine Umformung vorzunehmen.
a) x – 4 = 0
b) –x = 12
c) x = –23
d) y + 9,8 = 0
e)
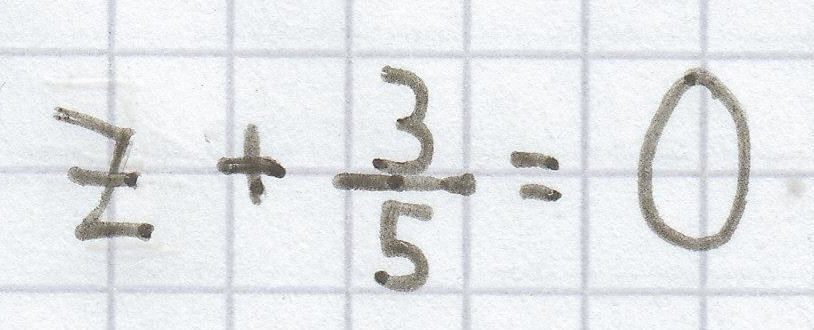
f) 3y = 18
g) y : 5 = 4
h) 7z = 56
i) x : 9 = 6
2. Mathe-Nachhilfe-Aufgabe: Gebe die Lösungsmenge folgender Produkt-Gleichungen an und dies ohne Umformungen an der Gleichung vorzunehmen.
a) (x – 3) · (x – 9) = 0
b) (x +12) · (x – 7) = 0
c) (x – 18) · (x + 14) = 0
d) (x + 7,2) · (x + 1,4) = 0
e) (x – 3,6) · (x + 3,6) = 0
f)

g)
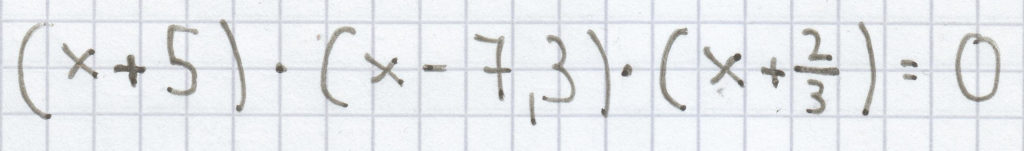
3. Mathe-Nachhilfe-Aufgabe: Bestimme die jeweilige Lösungsmenge der Gleichung.
a) y + 5 = y + 5
b) x + 9 = x + 11
c) x + 11 – 11 = 0
d) 9z + 2 = 9z +7
e) 0 · y = 0
f) (–5) · z – 5 = (–5) · z – 5
g) 0 · y = 1
4. Mathematik-Nachhilfe-Aufgabe: Finde unter den angegebenen Lösungen die Richtige für die Gleichung: 54 – (6x + 12) = 38 – 2 · (4x – 4).
Lösungen: x = 1; x = 0; x = –1; x = –2; x = 2
5. Mathematik-Nachhilfe-Aufgabe: Ermittle die richtige Lösungsmenge für folgende Gleichung: 0 = (x – 12) · x
Lösungsmengen: L = { }; L = Q; L = {0; 12 }; L = {–12, 0 }

Lösungen zum Mathematik-Stoffgebiet: Gleichungen
1. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Ermittlung der Lösung bei Gleichungen, indem das Ergebnis abgelesen wird.
a) x – 4 = 0; hier sieht man sofort, dass x = 4 die Lösung der Gleichung ist, da dann die Gleichung lautet: 4 – 4 = 0 <=> 0 = 0. Daher ist L = {4}. Das ist auch die einzige Lösung. Schließlich findet man bei linearen Gleichungen maximal ein passendes Ergebnis.
b) –x = 12; hier ist die Lösung x = –12. Denn dann wird die Gleichung „wahr“, da die Gleichung dann folgendermaßen aussieht: –(–12) = 12 <=> 12 = 12. Daher ist L = {–12}.
c) x = –23; die Lösung für diese Gleichung ist hier: –23. Setzt man diesen Wert in die Gleichung ein, dann ergibt sich folgende Gleichung: –23 = –23. Deshalb ist L = {–23}.
d) y + 9,8 = 0; die Lösung ist hier: –9,8. Denn beim Einsetzen dieses Wertes ergibt sich folgende Gleichung: –9,8 + 9,8 = 0 <=> 0 = 0. Deshalb ist L = {–9,8}.
e)
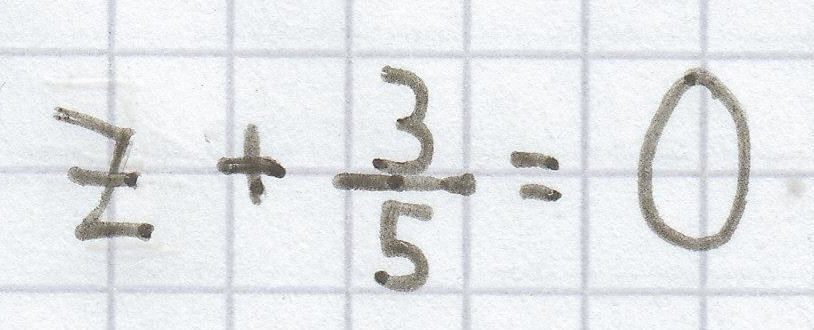
; bei dieser Gleichung ist die Lösung:

. Denn bei diesem Wert ergibt sich folgende Gleichung:
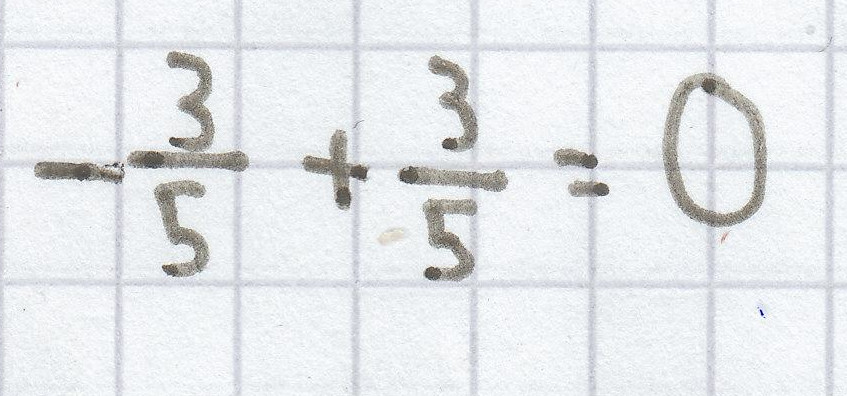
<=> 0 = 0.
Daher ist L =
{

}.
f) 3y = 18; hier kann man recht einfach sehen, dass die Gleichung bei y = 6 „wahr“ ist. Schließlich ergibt sich dann diese Gleichung: 3 · 6 = 18 <=>18 = 18. Deshalb ist L = {6}.
g) y : 5 = 4; bei dieser Gleichung ist die Lösung y = 20. Denn bei diesem Wert ergibt sich folgende Gleichung. 20 : 5 = 4 <=> 4 = 4. Daher ist L = {4}.
h) 7z = 56; hier ist die Lösung: z = 8. Schließlich ergibt sich aus diesem Wert folgende Gleichung: 7 · 8 = 56 <=> 56 = 56. Deshalb ist L = {8}.
i) x : 9 = 6; die Lösung für diese Gleichung ist x = 54. Denn bei diesem Wert ergibt sich folgende Gleichung: 54 : 9 = 6 <=> 6 = 6. Deshalb ist L = {54}.
2. Lösung zu der Mathe-Nachhilfe-Aufgabe: Gebe alle Lösungen zu den Gleichungen an, ohne hierbei eine Umformung vorzunehmen.
a) (x – 3) · (x – 9) = 0
Da ein Produkt immer null wird, wenn einer seiner Faktoren null wird, kann man bei folgender „Produkt-Gleichung“ die Lösung gleich ablesen: (x – 3) · (x – 9) = 0. Die Lösungsmenge ist daher hier: L = {3; 9}. Denn die Gleichung wird jeweils null und damit „wahr“, wenn man in einen der beiden Faktoren den Wert 3 oder den Wert 9 einsetzt.
b) (x +12) · (x – 7) = 0
Da hier ebenso eine „Produkt-Gleichung“ vorliegt, ist die Gleichung (x +12) · (x – 7) = 0 „wahr“ , wenn x = –12 ist oder x = 7. Daher ist L = {–12; 7}.
c) (x – 18) · (x + 14) = 0
Die Gleichung (x – 18) · (x + 14) = 0 ist „wahr“, wenn x = 18 oder x = –14 ist. Deshalb ist L = {–14; 18}.
d) (x + 7,2) · (x + 1,4) = 0
Was bei einer „Produkt-Gleichung“ für ganze Zahlen gilt, gilt ebenso für Dezimalzahlen. Deshalb ist die Gleichung (x + 7,2) · (x + 1,4) = 0 „wahr“, wenn x = –7,2 ist oder x = –1,4. Daher ist L = {–7,2; –1,4}.
e) (x – 3,6) · (x + 3,6) = 0
Die Gleichung (x – 3,6) · (x + 3,6) = 0 ist bei x = 3,6 und x = –3,6 „wahr“. Deshalb ist L = {–3,6; 3,6}.
f)

Was bei einer „Produkt-Gleichung“ für ganze Zahlen und Dezimalzahlen gilt, gilt ebenfalls für Bruchzahlen. Deshalb gilt für die Gleichung:

Die Aussage ist „wahr“ , wenn y folgenden Wert annimmt:
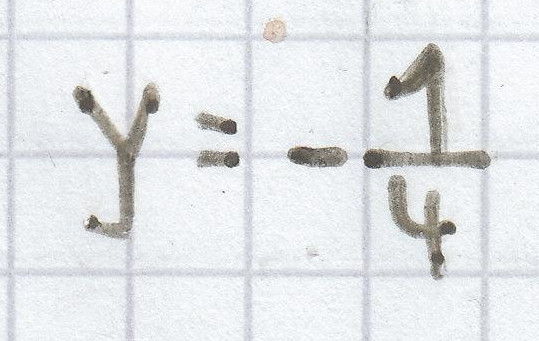
oder y = folgenden Wert annimmt:
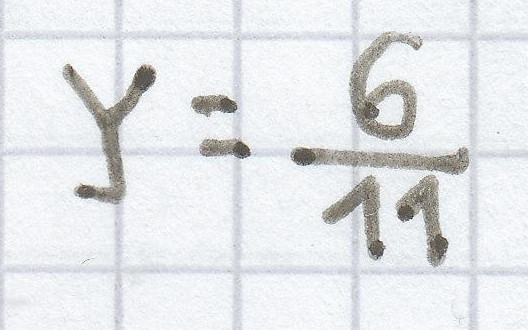
. Daher ergibt sich für die Gleichung als Lösung L =
{

;

}.
g)
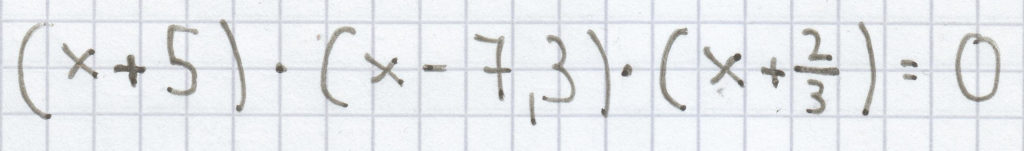
Aber auch wenn die „Produkt-Gleichung“ aus drei Faktoren besteht und diese sich aus ganzen Zahlen, Dezimalzahlen und Bruchzahlen zusammensetzt, kann man aus jener Gleichung sofort die Lösung ermitteln. Denn bei
x = –5
oder
x = 7,3
oder
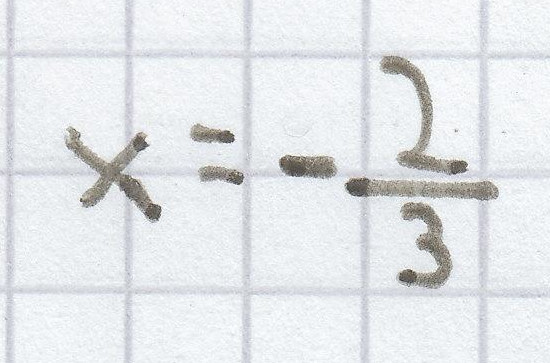
wird die Gleichung „wahr“.
Deshalb ist L =
{–5;

;
7,3}.
3. Lösung zu der Mathe-Nachhilfe-Aufgabe: Gebe jeweils die Lösungsmenge der Gleichung an.
a) y + 5 = y + 5
Wie man hier sieht, befindet sich bei y + 5 = y + 5 rechts und links des Gleichheitszeichens jeweils der identische Term. Daher ist bei jedem in die Variable eingesetzten Wert die Gleichung „wahr“. Deshalb ist je nach Klassenstufe L = Q bzw. R.
b) x + 9 = x + 11
Bei der Gleichung x + 9 = x + 11 ist zwar rechts und links des Gleichungszeichens die Variable jeweils gleich, die ganze Zahl aber nicht. Egal, welchen Wert man für die Variable einsetzt, das Ergebnis der Gleichung wird deshalb immer „unwahr“ sein. Deshalb ist L = { } beziehungsweise L = Ø.
c) x + 11 – 11 = 0
Wie man bei der Gleichung x + 11 – 11 = 0 sieht, ist nach der Elimination von + 11 – 11 die Lösung x = 0. Daher ist L = {0}
d) 9z + 2 = 9z +7
Bei der Gleichung 9z + 2 = 9z +7 ist jeweils die Variable samt Faktor gleich, die ganze Zahl aber nicht. Daher wird man hier auch keinen Wert für die Variable finden, damit die Gleichung „wahr“ wird. Daher ist L = { } beziehungsweise L = Ø.
e) 0 · y = 0
Bei der Gleichung 0 · y = 0 kann man für y jeden Wert einsetzen und die Gleichung wird „wahr“. Schließlich wird der Term mit der Variable immer null werden. Deshalb ist hier je nach Klassenstufe L = Q bzw. R.
f) (–5) · z – 5 = (–5) · z – 5
Wie man bei der Gleichung (–5) · z – 5 = (–5) · z – 5 sieht, sind die Terme rechts und links des Gleichheitszeichens identisch. Daher kann man in die Variable z jeden Wert einsetzen und das Ergebnis wird „wahr“. Deshalb ist je nach Klassenstufe L = Q bzw. R.
g) 0 · y = 1
Bei der Gleichung 0 · y = 1 kann man keinen Wert für y finden, damit die Gleichung „wahr“ wird. Schließlich wird der Term mit der Variable immer null werden. Daher ist hier L { } beziehungsweise L = Ø.
4. Lösung zu der Mathematik-Nachhilfe-Aufgabe: Ermittle unter den angegebenen Werten denjenigen, der eine Lösung folgender Gleichung ist: 54 – (6x + 12) = 38 – 2 · (4x – 4).
Lösungen: x = 1; x = 0; x = –1; x = –2; x = 2
Ein Möglichkeit diese Aufgabe zu lösen, ist nacheinander alle angegebenen Werte in die Variable x der Gleichung 54 – (6x + 12) = 38 – 2 · (4x – 4) einzusetzen.
Bei x = 1 ergibt sich dann folgende Gleichung:
54 – (6 + 12) = 38 – 2 · (4 – 4) <=> 54 – 18 = 38 – 2 · 0 <=> 36 = 38.
Wie man sieht, gibt dies eine „unwahre“ Aussage.
Bei x = 0 sieht die Gleichung folgendermaßen aus:
54 – (6 · 0 + 12) = 38 – 2 · (4 · 0 – 4) <=> 54 – (0 + 12) = 38 – 2 · (0 – 4) <=> 54 – 12 = 38 – 2 · – 4 <=> 42 = 38 + 8 = 42 = 46.
Auch hier entsteht eine „unwahre“ Aussage.
Bei x = –1 erhält man diese Gleichung:
54 – (6 · –1 + 12) = 38 – 2 · (4 · –1 – 4) <=> 54 – (–6 +12) = 38 – 2 · ( – 4 – 4) <=> 54 – 6 = 38 – 2 · – 8 <=> 48 = 38 + 16 <=> 48 = 54.
Ebenso ist diese Gleichung ist „unwahr“.
Bei x = –2 ergibt sich diese Gleichung:
54 – (6 · –2 + 12) = 38 – 2 · (4 · –2 – 4) <=> 54 – (–12 + 12) = 38 – 2 · (–8 – 4) <=> 54 – (0) = 38 – 2 · (–12) <=> 54 = 38 + 24 <=> 54 = 62.
Auch dies führt nicht zu einer „wahren“ Aussage.
Bei x = 2 erhält man folgende Gleichung:
54 – (6 · 2 + 12) = 38 – 2 · (4 · 2 – 4) <=> 54 – (12 + 12) = 38 – 2 · (8 – 4) <=> 54 – 24 = 38 – 2 · (4) <=> 30 = 38 – 8 <=> 30 = 30.
Wie man hier sieht, liefert x = 2 für die Gleichung eine „wahre“ Aussage. Daher ist L = {2}.
Eine andere, sicherlich schnellere Möglichkeit, die Gleichung zu lösen, geht über eine Auflösung der Gleichung nach der Variablen x hin:
54 – (6x +12) = 38 – 2 · (4x – 4) <=>
54 – 6x – 12 = 38 – 8x + 8 <=>
42 – 6x = 46 – 8x | + 8x/– 42 <=>
– 6x + 8x = 46 – 42 <=>
2x = 4 | : 2 <=>
x = 2
Wie man sieht, ergibt sich durch Auflösen der Gleichung nach der Variablen x hin auch die Lösung x = 2. Daher ist L = {2}.
5. Lösung der Mathematik-Nachhilfe-Aufgabe: Ermittle die richtige Lösungsmenge für die angegebene Gleichung: 0 = (x – 12) · x.
Lösungsmengen:
L = { }; L = ℚ; L = {0; 12 }; L = {–12, 0 }
Da es sich bei dieser Gleichung 0 = (x – 12) · x um eine Produktgleichung handelt, ist die Gleichung jeweils „wahr“, wenn einer der beiden Faktoren null wird. Das ist bei x = 12 und bei x = 0 der Fall. Daher ist L = {0; 12 } die richtige Lösungsmenge.