
Im Fach Mathematik müssen zum Lösen von Gleichungen fast immer Äquivalenzumformungen angewendet werden. Das sind Umformungen, wobei sich die Lösungsmenge der Ausgangsgleichung nicht ändert. Bei allen Grundrechenarten, „+“, „–“, „·“ und „:“, ist das auf jeden Fall gegeben, wenn hierbei immer nur gleiche Variablen und „nackte“ Zahlen zusammengefasst werden oder die „nackte“ Zahl von der Variable entfernt wird.
Entscheidend bei Äquivalenzumformungen ist nun vor allem, dass jede Äquivalenzumformung einen Schritt näher zur Lösung der Gleichung führen soll. Schließlich tickt in Mathe bei jeder Klassenarbeit und später auch ganz besonders im Abitur stets die Uhr, so dass man eigentlich immer ein Zeitproblem hat, wenn man nicht schnellstmöglich zielgerichtet Aufgaben löst.

Zunächst sollte man bei einer Gleichung immer schauen, ob man irgendwelche gleichartigen Einzelterme links und rechts des Gleichheitszeichens zusammenfassen kann. Danach beginnt man, jeweils einzelne Äquivalenzumformungen zu machen. Entweder man bringt als Erstes die Einzelterme mit Variable auf eine Seite der Gleichung oder die Einzelterme, die aus einer „nackten“ Zahl bestehen. Kenntlich macht man jede dieser Äquivalenzumformungen mit einem Operatorstrich ( „|“, wahlweise zusammen mit dem Äquivalenzzeichen „<=>“ – dieses immer mit zu machen, ist aber heutzutage in den Schulen nicht mehr so weit verbreitet) am rechten Ende der Gleichung plus der vorgenommenen Äquivalenzumformung. Ebenso dadurch, dass man wie beim Zusammenfassen von gleichartigen Einzeltermen hierzu jeweils auf dem Blatt eine Zeile tiefer geht. Darauf bringt man die Einzelterme, die nur eine „nackte“ Zahl vorweisen, auf die andere Seite beziehungsweise die Zahlen mit Variablen. Hierbei sollte man möglichst so die Gleichung äquivalent umformen, dass keine negativen Vorzeichen vor den übrigbleibenden Variablen und der „nackten“ Zahl entstehen. Schließlich entgeht man dadurch eventuellen Vorzeichenfehlern bei der Lösung der Gleichung. Hat man derart dann Äquivalenzumformungen vorgenommen, so hat man nahezu schon die Variable separiert – und ein eindeutiges Ergebnis der Gleichung. Denn jetzt muss man nur noch die Gleichung durch die Zahl teilen (bei Bruchzahlen macht immer auch eine Multiplikation, teilweise in Kombination mit einer Division, Sinn!), die vor der Variablen steht. Hat man dies schließlich gemacht, so zeigt sich ganz eindeutig die Lösung der Gleichung!
Ist man bei Äquivalenzumformungen schon fitter, so kann man immer auch gleich die zwei Umformungen, die die Variable auf die eine Seite und die „nackte“ Zahl auf die andere Seite bringen, auf einmal machen. Auch ist es ab einem bestimmten Können egal, ob hierbei negative Vorzeichen entstehen oder nicht, da dann trotzdem sicherlich keine Vorzeichenfehler auftreten werden. Jedenfalls sollte man beim Lösen von Äquivalenzumformungen eine gute Grundroutine entwickeln. Denn Äquivalenzumformungen stellen im Fach Mathe überaus wichtige elementare Algebra-Grundkenntnisse dar – und je besser man diese kann, desto schneller kann man dieses Mathematik-Handwerkszeug in Klassenarbeiten oder dem Abitur, aber auch bei der MSA-Prüfung abspulen.
Aufgaben zum Mathematik-Stoffgebiet Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Lege dar, welche Äquivalenzumformung genau durchgeführt wurde.
a)
x + 7 = 18
x = 11
b)
x – 3 = 12
x = 15
c)
3x = 18
x = 6
d)

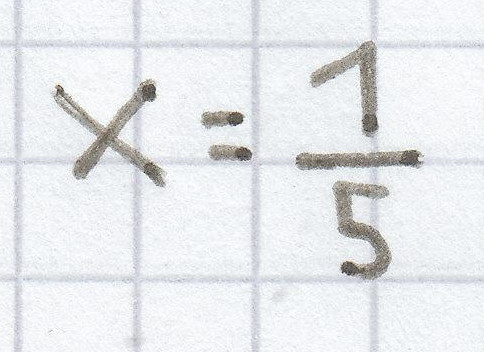
e)
x : 3 = 5
x = 15
f)
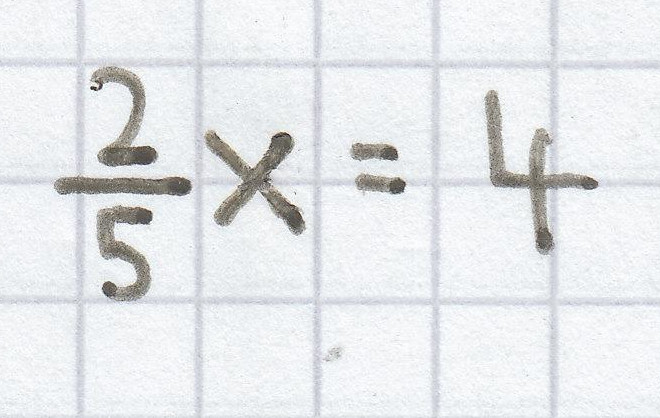
x = 10
g)

x = 1
h)
12x + 7 – 10x – 7 = 20
x = 10
2. Mathematik-Nachhilfe-Aufgabe: Nehme zur Lösung der Gleichung Äquivalenzumformungen vor.
a) x + 8 = 10,8
b) x – 9,4 = 12
c) (–12,5) + x = 4,8
d) 4x = 44
e) –8x = 112
f)

g)
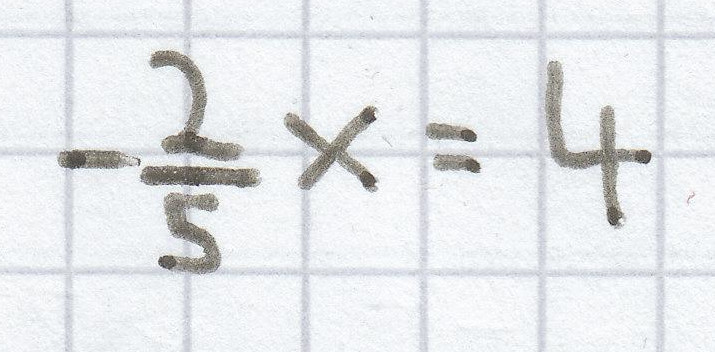
h)
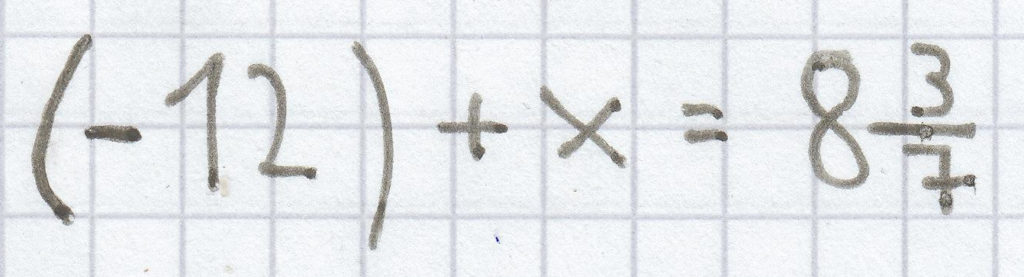
i)
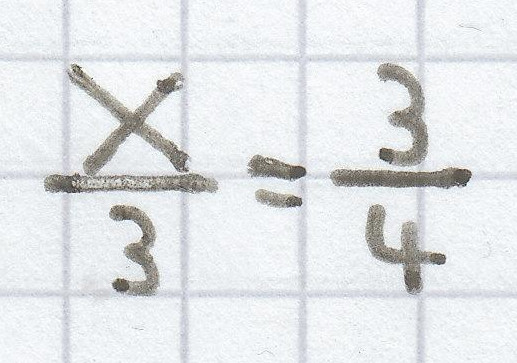
3. Mathematik-Nachhilfe-Aufgabe: Alle folgenden Gleichungen haben eine einzige Lösung. Zeige mittels Äquivalenzumformungen auf, welche dies ist.
a) 4x + 0 + x – 1 = 51
b) 7x – 5 + 7 – x = 68
c) 22 + 3x – 19 = 72
d) 16x + 4 + 7x + 3 = 191
e) 9x + 12 – 14 – 6x = 19
f) 55x – 22 – 34x = 251
4. Mathe-Nachhilfe-Aufgabe: Begründe, warum das Durchmultiplizieren der Gleichung 5x = 15 mit Null keine Äquivalenzumformung mehr ist. Tipp: Ziehe hier jeweils die beiden Lösungsmengen heran!
5. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge folgender Gleichungen.
a) x – x = 2
b) x – x = 0
c) 4x + 5 – 4x = 5
d) –9x + 2 = 2 –9x + 1
e) 3x + 2 – x · 3 = 4
f) (–7x) + 12 = (–7x)
g) x + x + 3 + 2x = 3 + 4x

Lösungen zu dem Mathematik-Stoffgebiet Gleichungen
1. Lösung der Mathe-Nachhilfe-Aufgabe: Nenne die ausgeführte Äquivalenzumformung.
a) Bei der Gleichung x + 7 = 18 wurde die Äquivalenzumformung „– 7“ durchgeführt, so dass dann die Gleichung zu x = 11 wurde.
b) Bei der Gleichung x – 3 = 12 wurde die Äquivalenzumformung „+ 3“ gemacht. Dadurch entstand schließlich die Gleichung x = 15.
c) Bei der Gleichung 3x = 18 wurdie die Äquivalenzumformung „: 3“ gemacht. Hierdurch ergab sich dann die Gleichung x = 6.
d) Bei der Gleichung

wurde die Äquivalenzumformung

durchgeführt, wodurch sich die Gleichung
x =
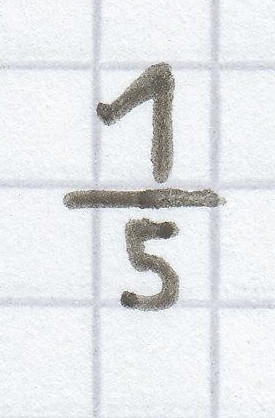
ergab.
e) Bei der Gleichung x : 3 = 5 wurde Äquivalenzumformung „· 3“ gemacht. Hierdurch ergab sich die Gleichung x = 15.
f) Bei der Gleichung
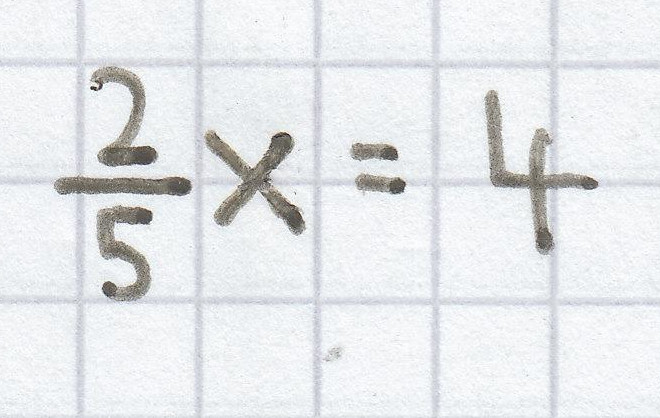
wurde die Äquivalenzumformung

durchgeführt. Dadurch entstand schließlich die Gleichung x = 10.
g) Bei der Gleichung

$wurde die Äquivalenzumformung

gemacht, wodurch sich die Gleichung x = 1 ergab.
h) Bei der Gleichung 12x + 7 – 10x – 7 = 20 wurden zunächst die gleichartigen Einzelterme „12x“ und „–10x“ sowie „7″ und „–7″ auf der einen Seite der Gleichung zusammengefasst. Hierdurch ergab sich die Gleichung 2x = 20. Anschließend wurde die Äquivalenzumformung „: 2“ durchgeführt, so dass sich die Gleichung x = 10 ergab.
2. Lösung der Mathe-Nachhilfe-Aufgabe: Löse die Gleichung mittels Äquivalenzumformungen.
a) x + 8 = 10,8 | – 8 <=> x = 2,8
Die Lösung der Gleichung ist folglich L = {2,8}.
b) x – 9,4 = 12 | + 9,4 <=> x = 21,4
Hier ist die Lösung der Gleichung L = {21,4}.
c) (–12,5) + x = 4,8 | + 12,5 <=> x = 17,3
Die Lösung der Gleichung ist folglich L = {17,3}.
d) 4x = 44 | : 4 <=> x = 11
Als Lösung der Gleichung ergibt sich hier demzufolge L = {11}.
e) –8x = 112 | : (–8) <=> x = –14
Hier ist die Lösung der Gleichung L = {–14}.
f)
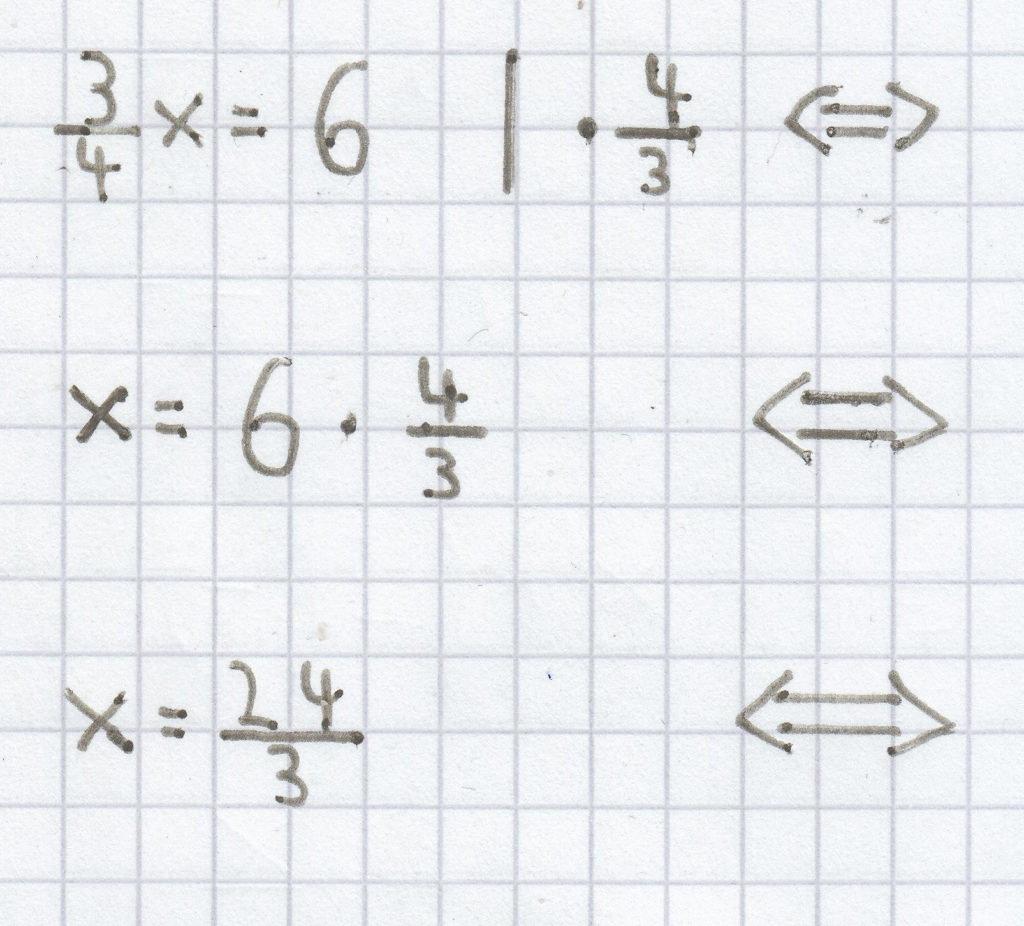
x = 8
Die Lösung der Gleichung ist folgliech L = {8}.
g)
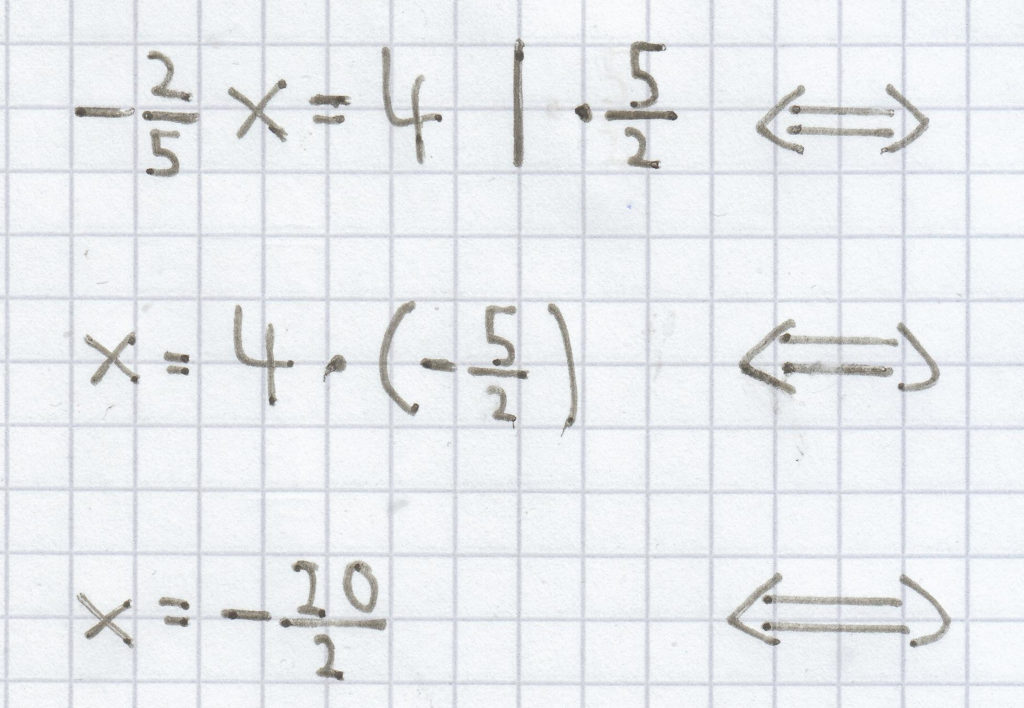
x = –10
Als Lösung der Gleichung ergibt sich also hier L = {–10}.
h)
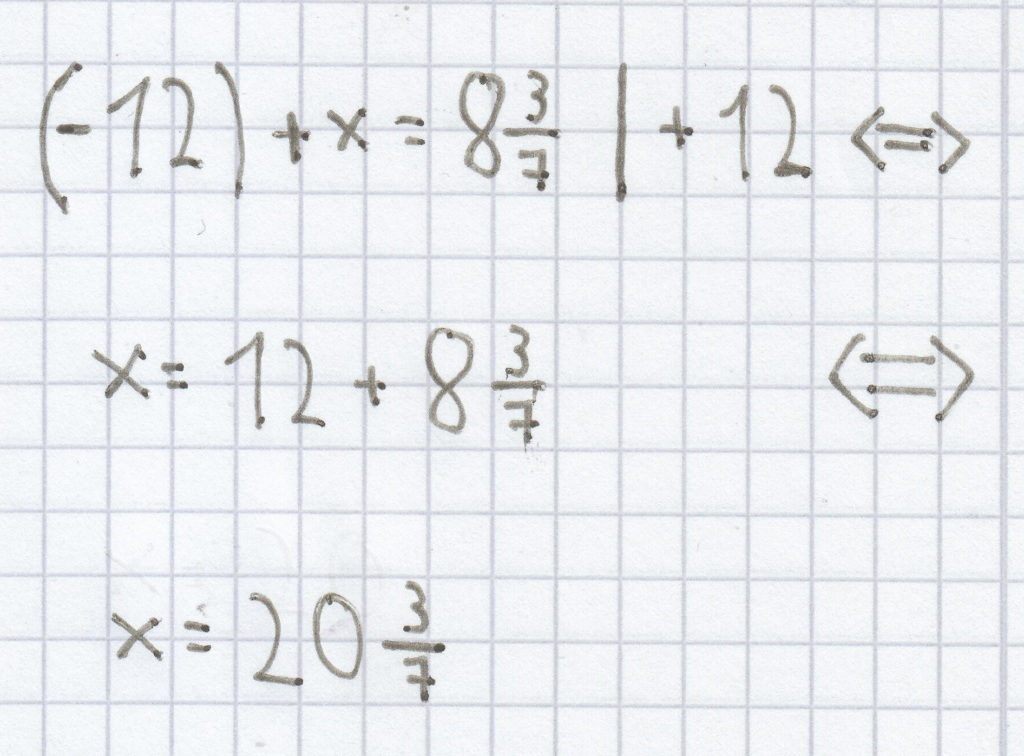
Die Lösung der Gleichung ist hier demzufolge
L =
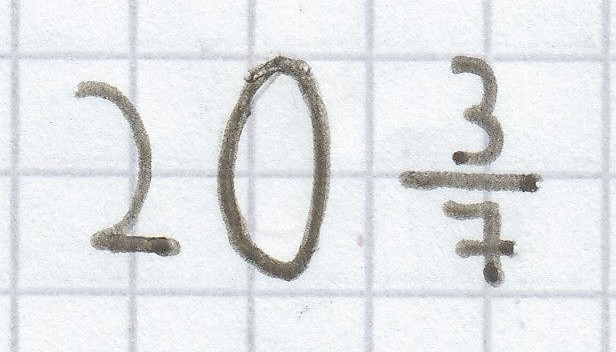
i)
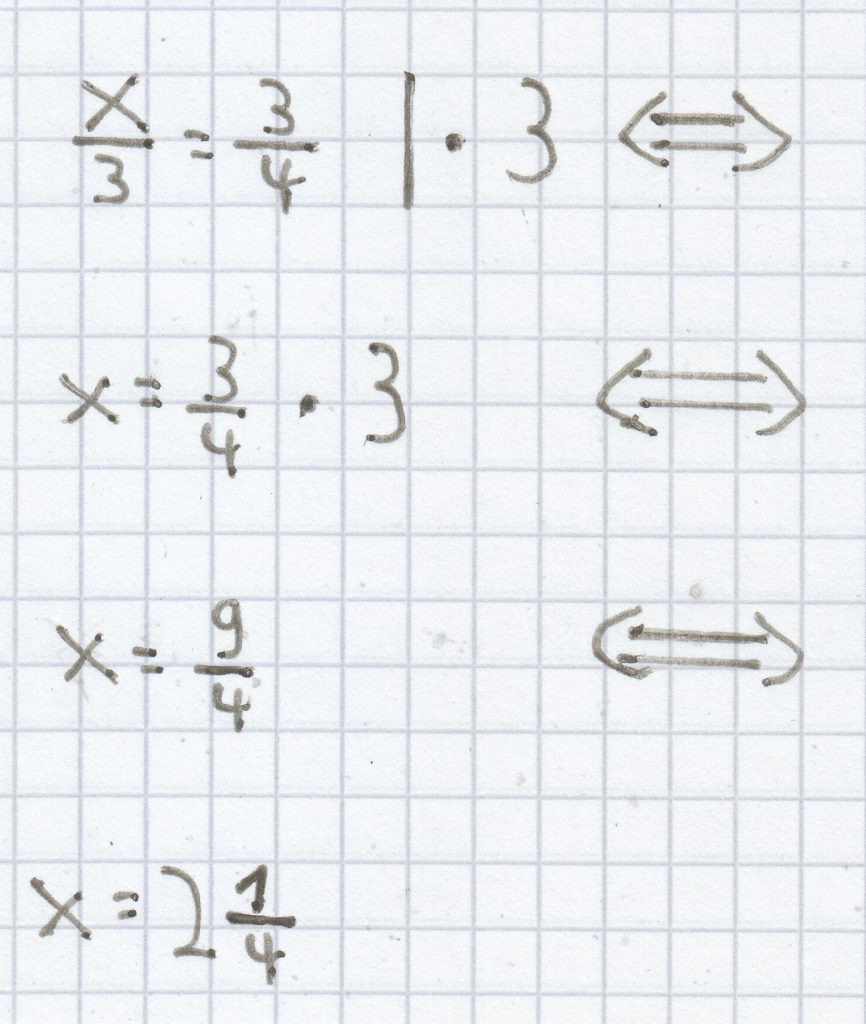
Die Lösung der Gleichung ist hier folglich
L =

.
3. Mathe-Nachhilfe-Aufgabe: Ermittle mittels Äquivalenzumformungen die Lösung der Gleichung.
a) 4x + 0 + x – 1 = 51 <=> 5x – 1 = 51 | + 1 <=> 4x = 52 | : 4 <=> x = 13
Die Lösung der Gleichung ist hier folglich L = {13}.
b) 7x – 5 + 7 – x = 68 <=> 6x + 2 = 68 | – 2 <=> 6x = 66 | : 6 <=> x = 11
Als Lösung der Gleichung ergibt sich hier L = {11}.
c) 22 + 3x – 19 = 72 <=> 3 + 3x = 72 | – 3 <=> 3x = 69 | : 3 <=> x = 23
Die Lösung der Gleichung ist hier demzufolge L = {23}.
d) 16x + 4 + 7x + 3 = 191 <=> 23x + 7 = 191 | – 7 <=> 23x = 184 | : 23 <=> x = 8
Die Lösung der Gleichung ist hier folglich L = {8}.
e) 9x + 12 – 14 – 6x = 19 <=> 3x – 2 = 19 | + 2 <=> 3x = 21 | : 3 <=> x = 7
Die Lösung der Gleichung ist hier demzufolge L = {7}.
f) 55x – 22 – 34x = 251 <=> 21x – 22 = 251 | + 22 <=> 21x = 273 | : 21 <=> x = 13
Als Lösung der Gleichung ergibt sich hier L = {13}.
4. Mathe-Nachhilfe-Aufgabe: Zeige auf, warum beim Durchmultiplizieren der Gleichung 5x = 15 mit Null keine Äquivalenzumformung mehr vorliegt.
Wie man recht einfach sehen kann, ist die Gleichung 5x = 15 „wahr“, wenn x = 3 ist. Dann ergibt sich nämlich 5 · 3 = 15 <=> 15 = 15.
Multipliziert man nun die Gleichung mit der Zahl Null durch, dann ändert sich jedoch die Lösungsmenge entscheidend! 5x = 15 | · 0 <=> 0 = 0.
Denn die Lösungsmenge ist nun unendlich, da jede Zahl eine Lösung liefert. Daher ist nun je nach Klassenstufe L = Q oder R. Damit hat man auch einen augenscheinlichen Beweis, dass das Duchmultiplizieren einer Gleichung mit der Zahl Null alles andere als eine Äquivalenzumformung ist!
5. Mathematik-Nachhilfe-Aufgabe: Bestimme jeweils die Lösungsmenge der Gleichung.
a) x – x = 2
Hier sieht man sofort, dass sich die Variable eliminiert und die Gleichung dadurch niemals mehr „wahr“ werden kann. Denn 0 = 2 ergibt ausschließlich als L = { } bzw. L = Ø.
b) x – x = 0
Hier kann man sofort sehen, dass die Variable sich ebenfalls eliminiert und somit die stets „wahre“ Gleichung 0 = 0 entsteht. Dieses führt dann zu L = Q bzw. R.
c) 4x + 5 – 4x = 5
Nach dem Zusammenfassen eliminiert sich bei dieser Gleichung ebenso die Variable, da man die Gleichung 5 = 5 erhält. Diese Gleichung hat wie bei Aufgabe b) eine unendlich große Lösungsmenge. Daher ist auch hier L = Q bzw. R.
d) –9x + 2 = 2 –9x + 1
Nach dem Zusammenfassen kann man sofort sehen, dass die Gleichung –9x + 2 = –9x + 3 keine Lösung liefert. Zwar eliminiert sich die Variable, aber es bleibt dafür die stets „unwahre“ Aussage 2 = 3 stehen. Daher ist hier L = { } bzw. L = Ø.
e) 3x + 2 – x · 3 = 4
Wie man schön sieht, eliminiert sich bei der Gleichung nach dem Zusammenfassen die Variable. Denn dann erhält man folgende Gleichung: 2 = 4. Diese Gleichung liefert folglich immer eine „unwahre“ Aussage. Daher ist hier L = { } bzw. L = Ø.
f) (–7x) + 12 = (–7x)
Auch bei dieser Gleichung eliminiert sich die Variable: (–7x) + 12 = (–7x) | +7x <=> 12 = 0. Die Gleichung bleibt daraufhin unlösbar. Daher ist hier ebenfalls L = { } bzw. L = Ø.
.
g) x + x + 3 + 2x = 3 + 4x
Nach dem Zusammenfassen erhält man diese Gleichung: 4x + 3 = 3 + 4x. Wie man unschwer erkennen kann, sind die Terme rechts und links des Gleichheitszeichens identisch. Daher ist hier L = Q bzw. R.