Warum ist es im Fach Mathematik sehr wichtig das Stoffgebiet Term gut verstanden zu haben? Ganz einfach. Ein Term ist das elementare Grundgebilde für Gleichungen und Funktionen. Daher kommen Terme in Mathe ab der Mittelstufe unentwegt vor. Zu sagen „Ich drücke mich um dieses Stoffgebiet“ heißt demzufolge: „Ich drücke mich um das ganze Fach Mathematik.“ Und das wäre natürlich alles andere als schlau. Irgendwann muss man dort auch mit ziemlich hoher Wahrscheinlichkeit eine Abschlussprüfung machen. Deshalb geht gewissermaßen kein Weg am Stoffgebiet Term vorbei. Aber mit einer gesunden Portion an Lernfleiß muss man sich auch keine Sorgen machen, dass es nicht auch bei dieser „mathematischen Materie“ irgendwann „klick“ macht. Denn auch das Stoffgebiet Term ist überaus gut lernbar – und das wie immer im Fach Mathe am besten anhand von Aufgaben.

Aufgaben zum Mathematik-Stoffgebiet Term
1. Mathematik-Nachhilfe-Aufgabe: Bestimme den Zahlenwert folgender Terme. Runde die Ergebnisse auf Zehntel.
a) 7,3 + 5 · (8,2 – 1,5)²
b) – (15,3 – 12,25) + 4²
c)
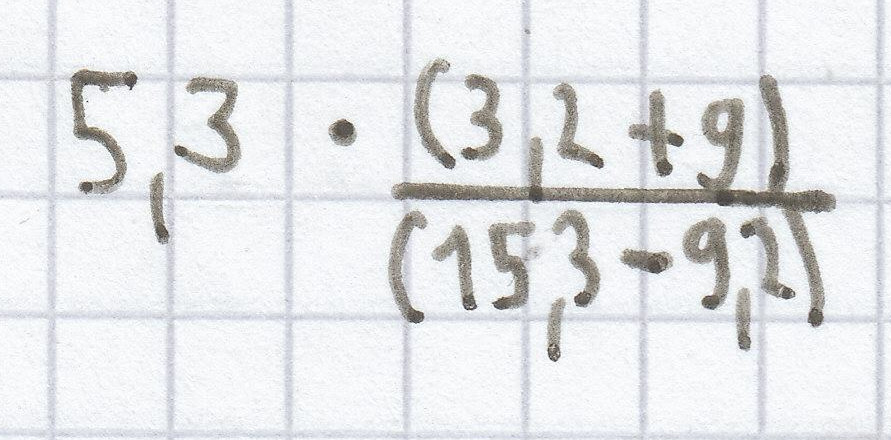
d)
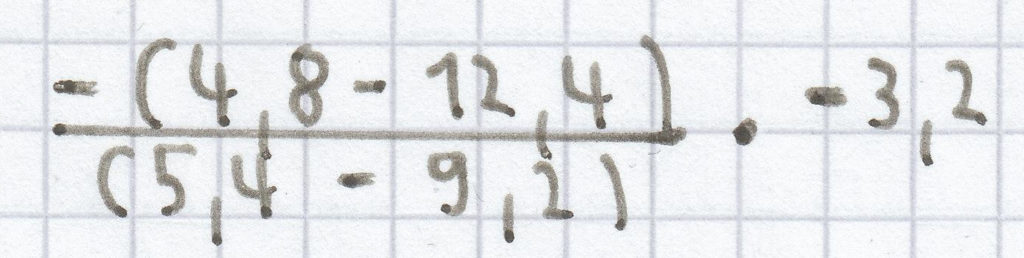
2. Mathematik-Nachhilfe-Aufgabe:Ermittle den jeweiligen Wert des Terms, indem nacheinander folgende Zahlen in die auftretende Variable eingesetzt werden: 3, 12, 0, –5, –19, 3,5, –3,8,

,
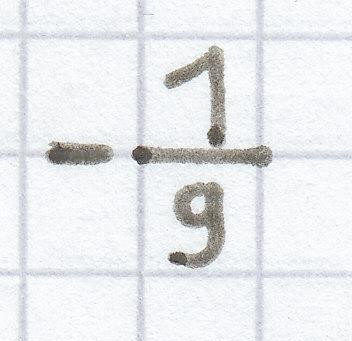
a) 5x + 9
b) 7x – 12
c) (9x +3) : 5
d) 8 + (x – 9) : 2
e) –5(3 – 2x)
3. Mathe-Nachhilfe-Aufgabe: Ermittle den Term.
a) In einer Murmelschachtel liegen noch x Murmeln. Erik nimmt ein Drittel aller Murmeln heraus, darauf nimmt Michael noch 3 weitere heraus.
b) Ein Quadrat hat die Seitenlänge x. Eine Seite wird nun um 7 cm verlängert. Stelle zunächst einen Term für den Flächeninhalt des ursprünglichen Quadrats auf, darauf einen Term für den neuen Flächeninhalt. Stelle ebenso einen Term für den Umfang des ursprünglichen Quadrats auf, darauf einen für den neuen Umfang.
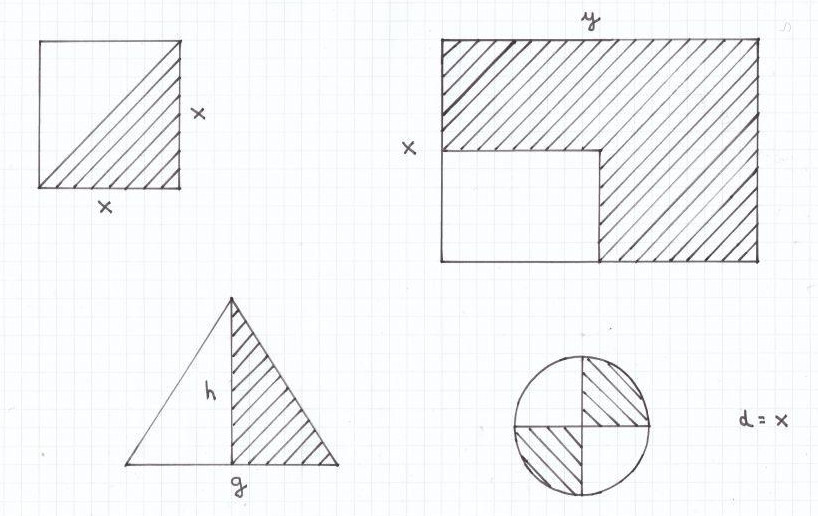
4. Mathe-Nachhilfe-Aufgabe: Auf der folgenden Abbildung sind verschiedene geometrische Flächen zu sehen. Gib jeweils einen Term für die darin hervorgehobenen gestreiften Flächen an. Verschiedene geometrische Flächen
5. Mathematik-Nachhilfe-Aufgabe: Setze jeweils in die Variable eine Zahl ein, so dass der Wert des Terms größer als 600 wird.
a) 2 x – 100
b) x : 500
c) 4 (x – 1000)
d) 0,02x – 400
e) (100 – 400) : 3x
Lösungen zum Mathe-Stoffgebiet Term
1. Lösung der Mathe-Nachhilfe-Aufgabe: Zahlenwerte der Terme berechnen und auf Zehntel hin runden.
a) 7,3 + 5 · (8,2 – 1,5)² = 7,3 + 5 ·(6,7)² = 7,3 + 5 · 44,89 = 7,3 + 224,45 = 321,75 = 231,8 (gerundet auf eine Nachkommastelle)
Anmerkung zum Rechenweg: Zuerst muss man die Klammer ausrechnen, dann die Potenz, danach das Produkt, zum Schluss die Summe! Auf Zehntel gerundet, heißt eine Stelle nach dem Komma.
b) – (15,3 – 12,25) + 4² = – (3,05) + 4² = –3,05 + 4² = –3,05 + 16 = 12,95 = 13 (gerundet auf eine Nachkommastelle)
Anmerkung: Zuerst muss man die Klammer ausrechnen. Hierbei kann man auch schon die Potenz ausrechnen oder dies erst später machen, danach die Minusklammer auflösen und zum Schluss die Summe zusammenfassen.
c)
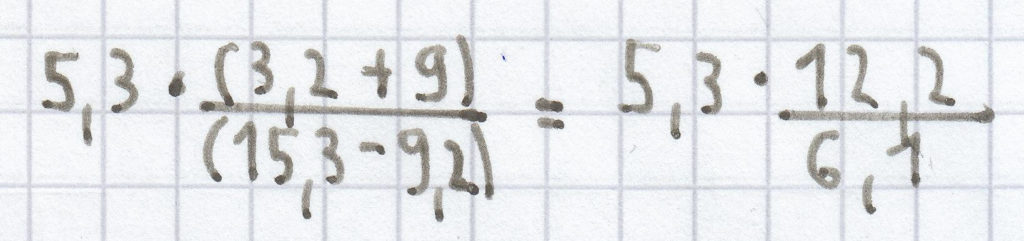
= 5,3 · 2 = 10,6
Anmerkung: zuerst den Zähler und den Nenner des Bruchs ausrechnen, dann den Nenner durch den Zähler teilen und zum Schluss das Produkt ausrechnen.
d)
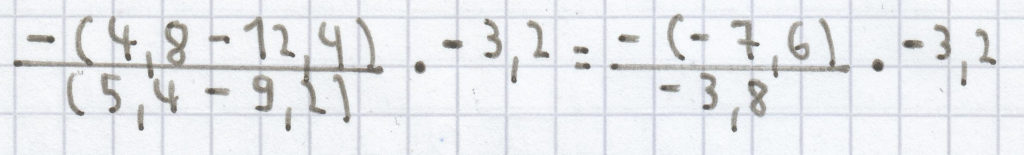
– (2) · –3,2 = – 2 · –3,2 = 6,4
Anmerkung: zuerst den Zähler und den Nenner des Bruchs ausrechnen, danach den Nenner durch den Zähler dividieren, dann die Minusklammer auflösen und zum Schluss das Produkt ausrechnen.
2. Lösung der Mathe-Nachhilfe-Aufgabe: Ermittle den Wert des Terms durch Einsetzen der Zahlen 3, 12, 0, –5, –19, 3,5, –3,8,

,
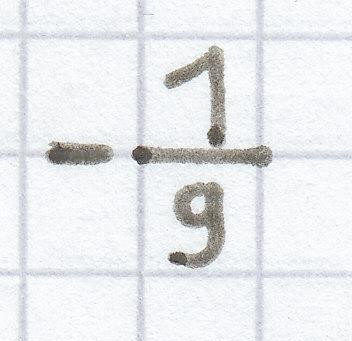
in die Variable.
a) für x = 3: 5 · 3 + 9 = 15 + 9 = 24;
für x =12: 5 · 12 + 9 = 60 + 9 = 69;
für x = 0: 5 · 0 + 9 = 0 + 9 = 9;
für x = –5: 5 · –5 + 9 = –25 + 9 = –16;
für x = –19: 5 · –19 + 9 = –95 + 9 = –86;
für x = 3,5: 5 · 3,5 + 9 = 17,5 + 9 = 26,5;
für x = –3,8: 5 · –3,8 + 9 = –19 + 9 = –10;
für x =

:
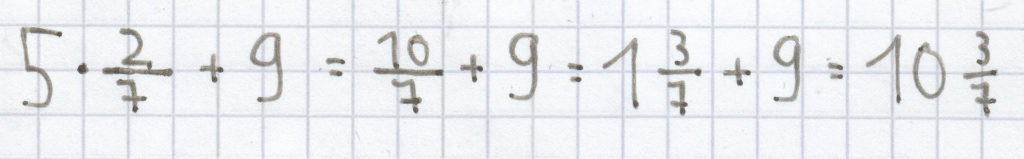
;
für x =
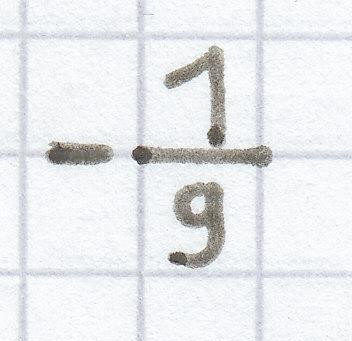
:
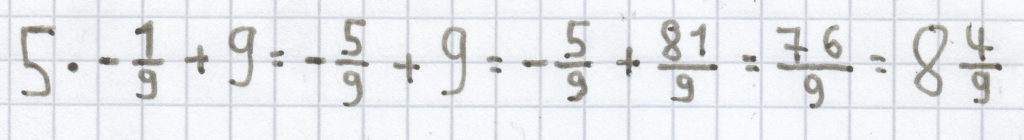
b) für x = 3: 7 · 3 – 12 = 21 – 12 = 9;
für x = 12: 7 · 12 – 12 = 84 – 12 = 72;
für x = 0: 7 · 0 – 12 = 0 – 12 = – 12; für x = –5: 7 · –5 – 12 = –35 – 12 = –47;
für x = –19: 7 · –19 – 12 =–133 – 12 = –145;
für x = 3,5: 7 · 3,5 – 12 = 24,5 – 12 = 12,5;
für x = –3,8: 7 · –3,8 – 12 =–26,6 – 12 = –38,6;
für x =

:
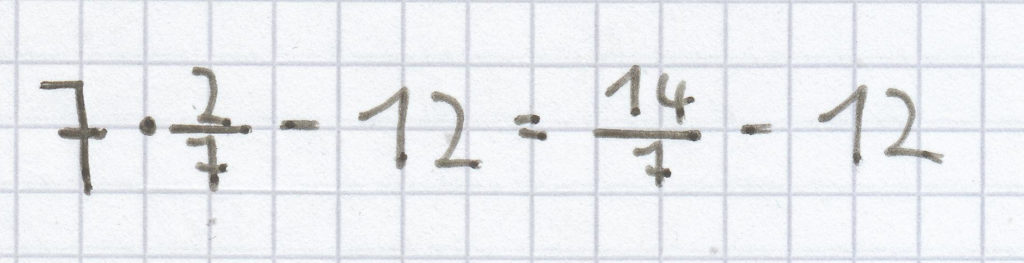
= 2 – 12 = –10;
für x =
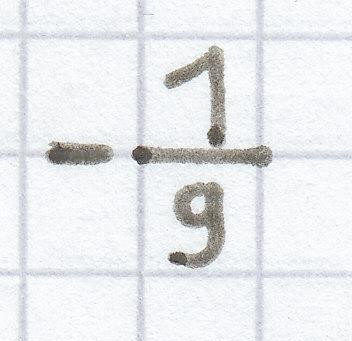
:
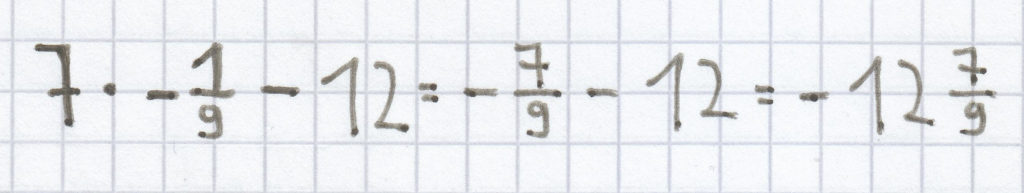
c) für x = 3: (9 · 3 + 3) : 5 = (27 + 3) : 5 = 30 : 5 = 6;
für x = 12: (9 · 12 + 3) : 5 = (108 + 3) : 5 = 111 : 5 = 22,2;
für x = 0: (9 · 0 +3) : 5 = (0 + 3) : 5 = 3 : 5 = 0,6;
für x = –5: (9 · –5 + 3) : 5 = (–45 + 3) : 5 = –42 : 5 = –8,4; für x = –19: (9 · –19 + 3) : 5 = (–171 + 3) : 5 = –168 : 5 = –33,6;
für x = 3,5: (9 · 3,5 + 3) : 5 = (31,5 + 3) : 5 = 34,5 : 5 = 6,9;
für x = –3,8: (9 · –3,8 + 3) : 5 = (–34,2 + 3) : 5 = –31,2 : 5 = –6,24;
für x =

:
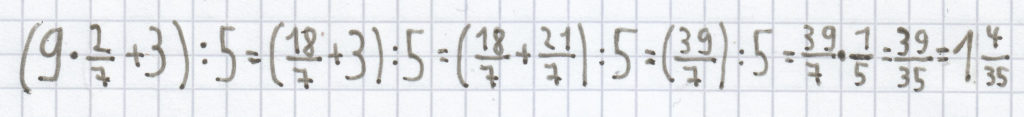
;
für x =
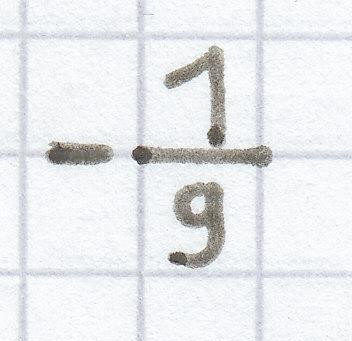
:
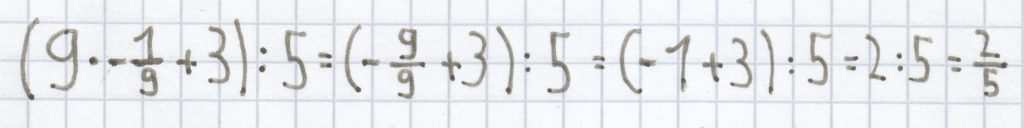
= 0,4
d) für x = 3: 8 + (3 – 9) : 2 = 8 + (–6) : 2 = 8 + (–3) = 5;
für x = 12: 8 + (12 – 9) : 2 = 8 + 3 : 2 = 8 + 1,5 = 9,5;
für x = 0: 8 + (0 – 9) : 2 = 8 + (– 9) : 2 = 8 + (–4,5) = 3,5;
für x = –5: 8 + (–5 – 9) : 2 = 8 + (–14) : 2 = 8 + (–7) = 1;
für x = –19: 8 + (–19 – 9) : 2 = 8 + (–28) : 2 = 8 + (–14) = –6;
für x = 3,5: 8 + (3,5 – 9) : 2 = 8 + (–5,5) : 2 = 8 + (–2,75) = 5,25;
für x = –3,8: 8 + (–3,8 – 9) : 2 = 8 + (–12,8) : 2 = 8 + (–6,4) = 1,6;
für x =

:
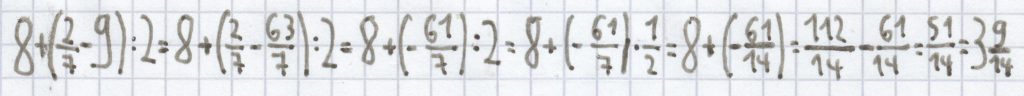
;
für x =
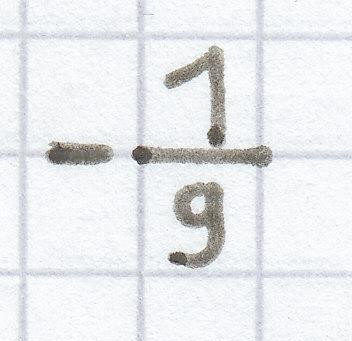
:
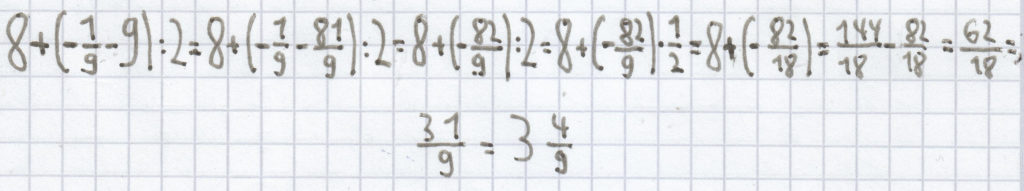
e) für x = 3: –5(3 – 2 · 3) = –5(3 – 6) = –5(–3) = 15;
für x = 12: –5(3 – 2 · 12) = –5(3 – 24) = –5(–21) = 105;
für x = 0: –5(3 – 2 · 0) = –5(3 – 0) = –5(3) = –15;
für x = –5: –5(3 – 2 · –5) = –5: –5(3 – (–10)) = –5: –5(3 + 10) = –5: –5(13) = –65;
für x = –19: –5(3 – 2 · –19) = –5(3 – (–38)) = –5(3 + 38) = –5(41) = – 205;
für x = 3,5: –5(3 – 2 · 3,5) = –5(3 – 7) = –5(–4) = 20;
für x = –3,8: –5(3 – 2 · –3,8) = –5(3 – (–7,6) = –5(3 + 7,6) = –5(10,6) = –53;
für x =

:
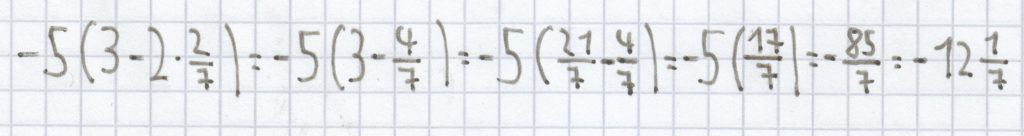
;
für x =
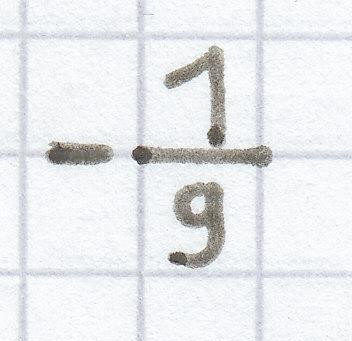
:
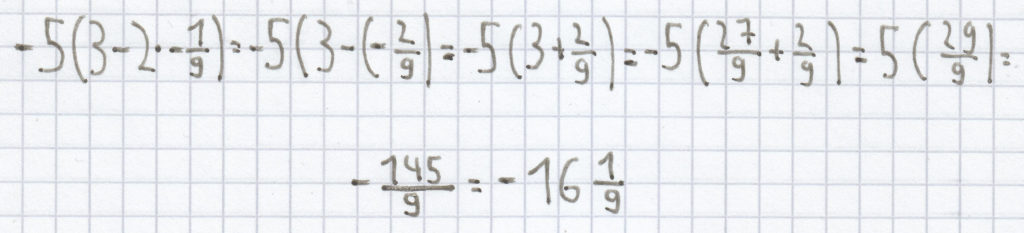

3. Lösung der Mathematik-Nachhilfe-Aufgabe: Stelle den Term auf.
a) Der gesuchte Term ist hier folgender:

.
Hierbei ist x die Gesamtzahl aller Murmeln.
b) Der Flächeninhalt eines Quadrats ist Länge · Lange. Demzufolge ergibt sich für den gesuchten Term: x · x = x²; nachdem eine Seite um 7 cm verlängert worden ist, ergibt sich nun dieser neue Term für den Flächeninhalt des jetzt entstandenen Rechtecks: x · (x + 7).
Der Umfang eines Quadrats ergibt sich aus der Summe aller Längen: x + x + x + x = 4x; der Umfang des neu entstandenen Rechtecks ergibt sich ebenso aus der Summe aller Längen und ist demzufolge: x + x + x + 7 + x + 7 = 4 x +14.
4. Lösung der Mathe-Nachhilfe-Aufgabe: Term-Aufstellung bei vorgegebener Zeichnung.
Bei dem Quadrat ist die Hälfte der Fläche gestrichelt. Die komplette Fläche eines Quadrats ergibt sich durch die Multiplikation zweier Seiten. Daher ist hier der gesuchte Term: (x · x) : 2 =

beziehungsweise
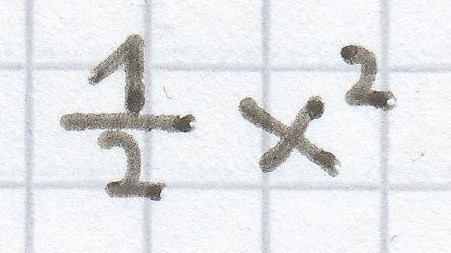
.
Bei dem Rechteck ist drei Viertel der Fläche gestrichelt. Die komplette Fläche eines Rechtecks ergibt sich durch die Multiplikation von Länge und Breite. Daher ist der gesuchte Term hier folgender: ((x · y) · 3 ) : 4 =
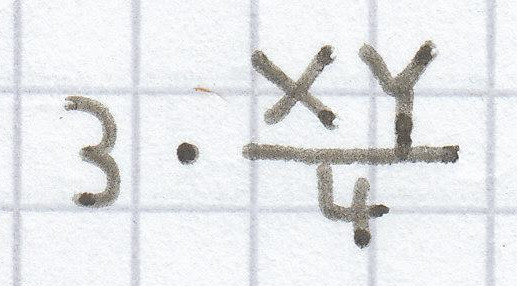
beziehungsweise
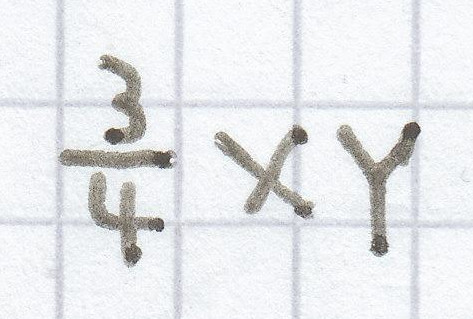
.
Bei dem Dreieck ist die Hälfte der Fläche gestrichelt. Die komplette Fläche eines Dreiecks ergibt sich durch Multiplikation von Grundseite und Grundseiten-Höhe geteilt durch 2. Der gesuchte Term ist deshalb hier: ((g · h) : 2) : 2 =

.
Bei dem Kreis ist die Hälfte der Fläche gestrichelt. Die komplette Fläche eines Kreises ergibt sich durch die Multiplikation von der Kreiszahl Π und des Durchmessers im Quadrat, wobei dann noch das Produkt durch 4 geteilt werden muss. Der gesuchte Term ist hier folgender:
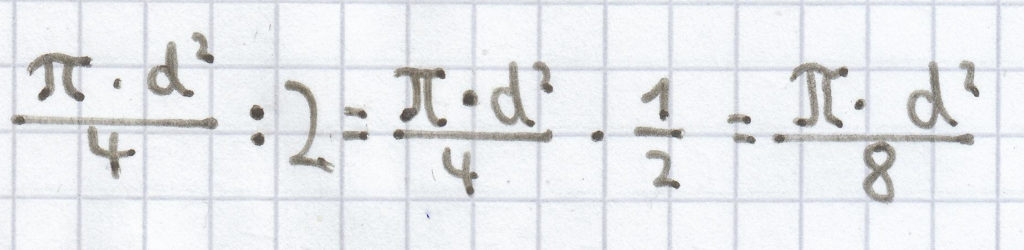
.
5. Lösung der Mathe-Nachhilfe-Aufgabe: Welche in die Variable eingesetzte Zahl macht den Wert des Terms größer als 600?
Am schnellsten löst man diese Aufgabe durch das Einsetzen von Zahlen. Man muss ja nur eine einzige Zahl finden, damit die Wert-Vorgabe erfüllt ist.
a) Alle in die Variable eingesetzten Zahlen größer „350“ erfüllen die Wert-Vorgabe.
b) Alle in die Variable eingesetzten Zahlen größer „300000“ passen zur Wert-Vorgabe.
c) Alle in die Variable eingesetzten Zahlen größer „1150“ erfüllen die Wert-Vorgabe.
d) Alle in die Variable eingesetzten Zahlen größer „50000“ erfüllen die Wert-Vorgabe
e) Alle in die Variable eingesetzten Zahlen größer
„
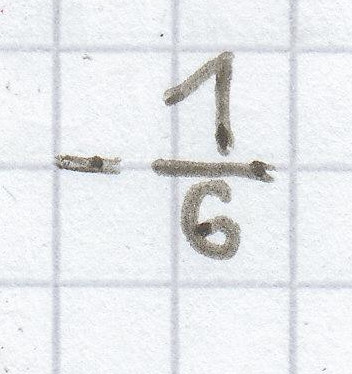
“ und kleiner „0“ passen zur Wert-Vorgabe.