Ohne es oft zu wissen, sind wir um uns herum von Punktsymmetrien umgeben. Der Schilderwald im Straßenverkehr hat vielfach eine punktsymmetrische (und auch achsensymmetrische) Symbolik. Das Gleiche gilt für Spielkarten und Spielflächen sowie im Stile eines englischen Landschaftsgarten angelegte Parkflächen. Aber auch unser Alphabet besteht aus Buchstaben, die eine Punktsymmetrie vorweisen. Wie erkennt man aber diese bzw. wann genau ist etwas punktsymmetrisch? In der Mathematik ist eine Punktsymmetrie nichts anderes als eine Punktspiegelung. Jeder Punkt einer bestimmten Figur wird mittels Halbdrehung (180 º) an einem bestimmten Punkt, dem Symmetriezentrum M, gespiegelt. Ist das bei einer Figur, die man sieht, der Fall, so liegt augenscheinlich eine Punktspiegelung vor.
Aufgaben zum Mathe-Stoffgebiet Punktspiegelung
1. Mathe-Nachhilfe-Aufgabe: Suche im Alltag vorkommende Punktsymmetrien. Denke an Verkehrssymbole, Karten- und Brettspiele, Automarken und Flaggen.
2. Mathematik-Nachhilfe-Aufgabe: Finde Buchstaben und Ziffern, die jeweils punktsymmetrisch sind.
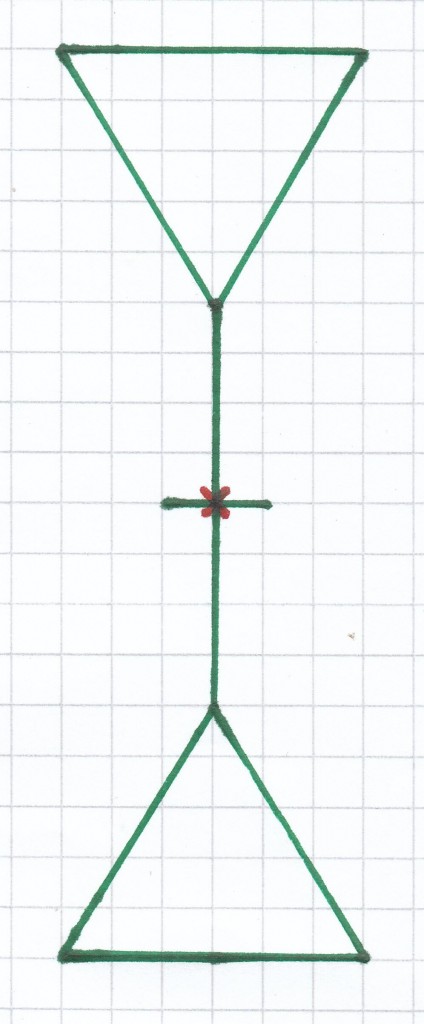
3. Mathe-Nachhilfe-Aufgabe: Folgende Abbildungen sollen eine Punktsymmetrie vorweisen. Das rote Kreuz stellt das Symmetriezentrum dar.
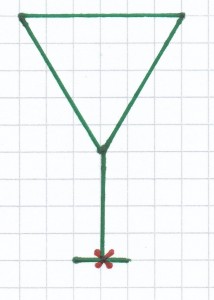
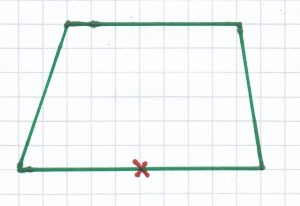

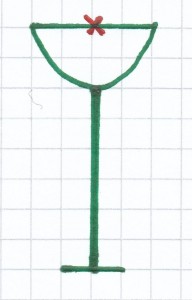

4. Mathematik-Nachhilfe-Aufgabe: Überlege, welche Figuren punktsymmetrisch sind. Bestimme bei vorhandener Punktsymmetrie das Symmetriezentrum.
a) Gerade
b) Kreis
c) Strecke
d) Halbgerade
e) Geradenkreuzung
f) Winkel
g) Parallelenpaar

Lösungen zum Mathematik-Stoffgebiet Punktspiegelung
1. Mathematik-Nachhilfe-Aufgabe: Wo gibt es im Alltag Punktsymmetrien? Orientiere dich an Verkehrsschildern, Karten- und Brettspielen, Automarken sowie Flaggen.
Das weiß-gelbe Vorfahrtszeichen ist punktsymmetrisch; das rot-blaue Verkehrsschild fürs absolute Halteverbot ebenso; das rot-blaue Verkehrsschild „eingeschränktes Halteverbot“ auch; das rot-weiße Verbot für die Einfahrt auch; das rot-weiße Verbot für alle Fahrzeuge ebenso; das blau-weiß-rote Verkehrsschild „Erste Hilfe“ auch. Bei Karten ist das sogenannte Französische Blatt, womit man beispielsweise Skat spielt, punktsymmetrisch (ausgenommen das Herz Ass, das Pik Ass und das Kreuz Ass, das Karo Ass ist wiederum punktsymmetrisch); beim deutschen Blatt, womit man Schafkopf spielt, sind alle Karten punktsymmetrisch; beim Brettspiel Halma ist die Spielfläche (siehe Bild) punktsymmetrisch; die Spielfläche von Mühle und Schach ebenso; auch die Spielfläche von Backgammon ist punktsymmetrisch sowie die von Solitär. Das Symbol für die Automarke Renault ist punktsymmetrisch; das von Audi ebenso; das von Nissan und Suzuki auch; das Automarken-Symbol von Chevrolet ist auch punktsymmetrisch; auch das von Opel; ebenso das von Seat. Die Flagge von Österreich ist punktsymmerisch, ebenso die Flagge von Jamaika; die Flaggen von Großbritannien und Mazedonien ebenso; die Flagge von Botswana ist auch punktsymmetrisch; auch die Flagge von Costa Rica; ebenso die von Georgien; auch die von Israel und Japan; die Flaggen von Laos und Lettland sind auch punktsymmetrisch; ebenso die von den Föderierten Staaten von Mikronesien; ebenso die von Nigeria und Peru; auch die Flagge von der Schweiz ist punktsymmetrisch; auch die von Thailand.
2. Mathe-Nachhilfe-Aufgabe: Welche Buchstaben und Ziffern sind punktsymmetrisch?
Der Buchstabe H ist punktsymmetrisch; der Buchstabe I ebenso; der Buchstabe O auch; der Buchstabe S auch; ebenso sind die Buchstaben X und Z punktsymmetrisch. Die Zahl 0 ist punktsymmetrisch; ebenso die Zahl 8. Alle weiteren Zahlen, die nur aus der Zahl 8 bestehen, sind ebenfalls punktsymmetrisch, wie die 88, 888, 8888 usw.; aber auch Zahlen, in denen zwischen zwei Achten eine Null steht, wie 808; 8080808; 80808080808 usw.
3. Mathematik-Nachhilfe-Aufgabe: Ergänze folgende Figuren so, dass eine Punktsymmetrie vorliegt.
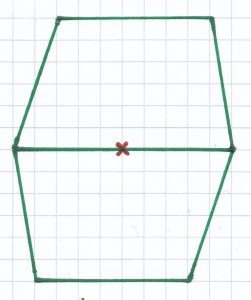

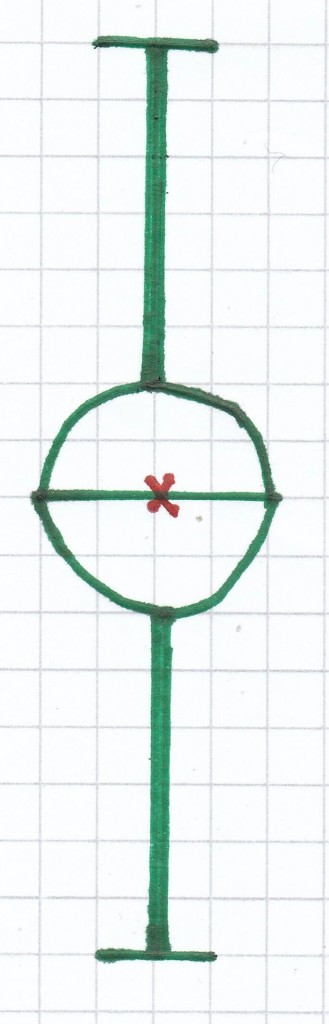
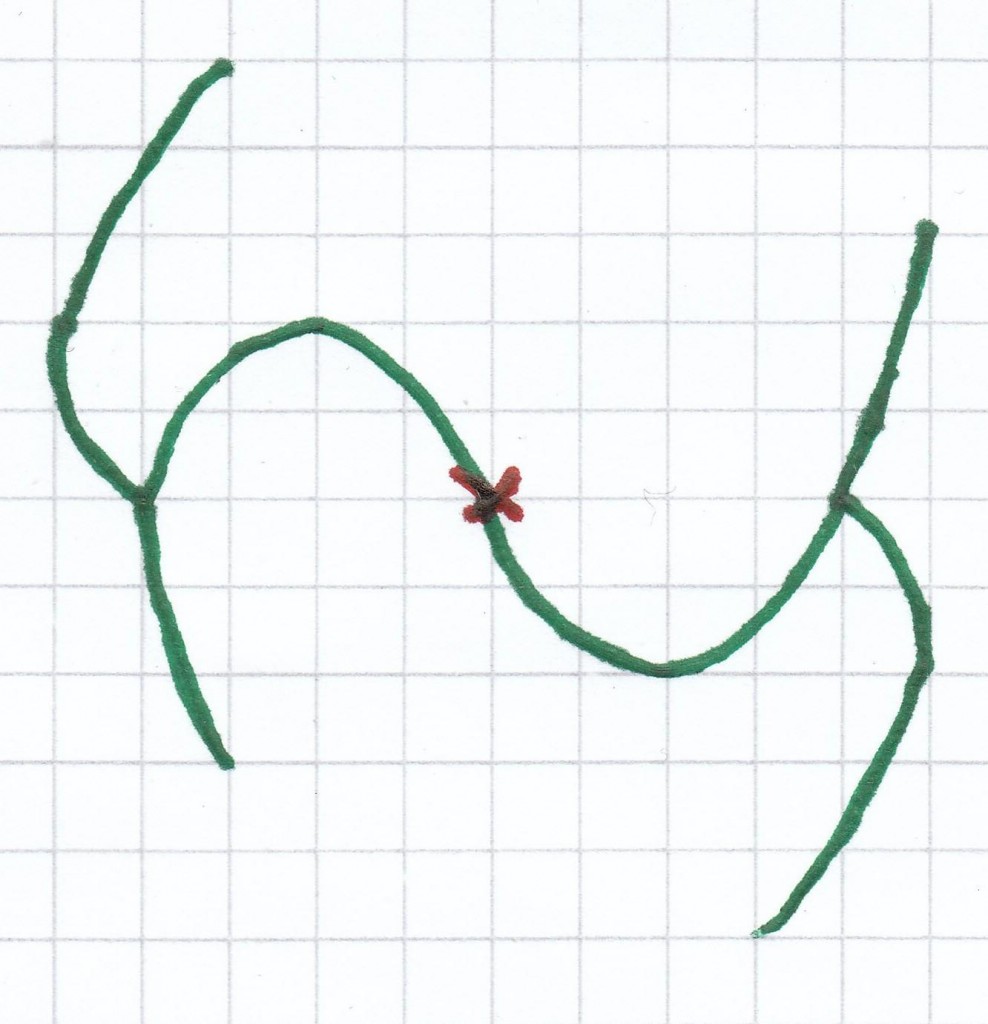
4. Mathe-Nachhilfe-Aufgabe: Welche der Figuren sind punktsymmetrisch. Ermittle bei bestehender Punktsymmetrie das Symmetriezentrum.
Bei jeder Figur muss man sich überlegen, ob eine Halbdrehung bzw. eine Drehung um 180º eine Punktsymmetrie ergibt. Gedanklich dreht man einfach die Figur und überlegt, ob diese gewissermaßen auf sich selbst abgebildet wird. Ist das der Fall, liegt eine Punktsymmetrie vor und man kann auch ein Symmetriezentrum ermitteln.
a) Gerade
Eine Gerade ist ja unendlich lang und das jeweils an beiden Enden. Dreht man sie um 180º, so liegt auf jeden Fall eine Punktsymmetrie vor. Sie wird ja dann direkt wiederum auf sich abgebildet. Aufgrund der unendlichen Länge ergeben sich aber auch unendlich viele Symmetriezentren auf einer Geraden.
b) Kreis
Beim Kreis liegt ebenfalls eine Punktsymmetrie vor. Das Symmetriezentrum ist der Mittelpunkt des Kreises.
c) Strecke
Hier liegt wiederum eine Punktsymmetrie vor. Das Symmetriezentrum ist der Mittelpunkt der Strecke.
d)) Halbgerade
Hier liegt keine Punktsymmetrie aufgrund der Begrenzung auf einer Seite vor.
e) Geradenkreuzung
Jede Geradenkreuzung ist punktsymmetrisch. Schneiden sich zwei Geraden, so entstehen ja immer zwei gegenüberliegende Winkel die gleich groß sind. Das Symmetriezentrum stellt der Schnittpunkt der beiden Geraden dar.
f) Winkel
Ein Winkel ist normalerweise nicht punktsymmetrisch.
g) Parallelenpaar
Ein Parallelenpaar ist immer punktsymmetrisch. Es gibt hierbei unendlich viele Symmetriezentren, und zwar auf der Geraden, die genau in der Mitte des Parallelenpaars verläuft.