Zauberquadrate (auch Magische Quadrate genannt) sollen Kindern helfen, die Addition und die Subtraktion zu üben. Gewöhnlich ist ein Zauberquadrat ein 3×3-Gitter, was 9 Felder hat. Wenn in einer Spalte eine 4, eine 9 und eine 2 darin sind, muss man diese Zahlen zusammenaddieren (siehe Beispiel unten, die erste Spalte). Das Ergebnis ist hierbei 15. Egal ob die Zahlen auch diagonal (schräg), senkrecht (von oben nach unten) oder waagerecht (von links nach rechts) addiert werden, müssen diese dann immer 15 ergeben (die gleiche Summe). Dieses Ergebnis, z. B. hier die 15, nennt man Magische Zahl. Wichtig ist: dass die Zahlen, die zusammenaddiert die Magische Zahl ergeben, in einem Zauberquadrat jeweils nur 1-mal vorkommen dürfen, also nicht doppelt!
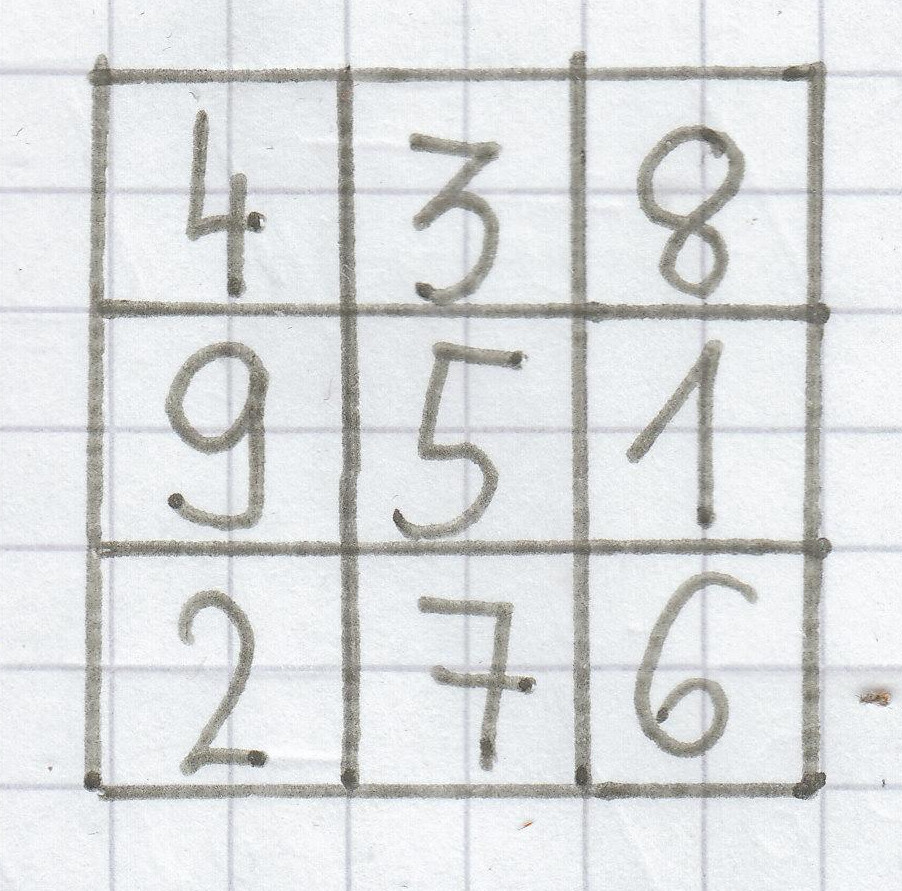
In der zweiten Spalte ergibt 3 + 5 + 7 wiederum 15 und in der dritten Spalte 8 + 1 + 6 erneut 15. Die erste Zeile mit den Zahlen 4, 3 und 8 wird auch addiert. Hier ist die Summe, das Ergebnis, auch 15. Die zweite Zeile 9 + 5 + 1 muss logischerweise auch 15 ergeben. Die dritte Zeile 2 + 7 + 6 hat auch 15 als Summe. Die Diagonale von links oben bis nach rechts unten, 4 + 5 + 6 addiert, hat wieder das Ergebnis 15. Die andere Diagonale ergibt, wenn man die Zahlen 8, 5 und 2 addiert, ebenso 15. Somit ergeben alle Spalten, Zeilen und Diagonalen die Magische Zahl, die in diesem Beispiel 15 beträgt.
Bei diesem Zauberquadrat ist die Magische Zahl 30. Wenn man jede Spalte, jede Zeile und jede Diagonale addiert, erhält man immer die Summe 30.
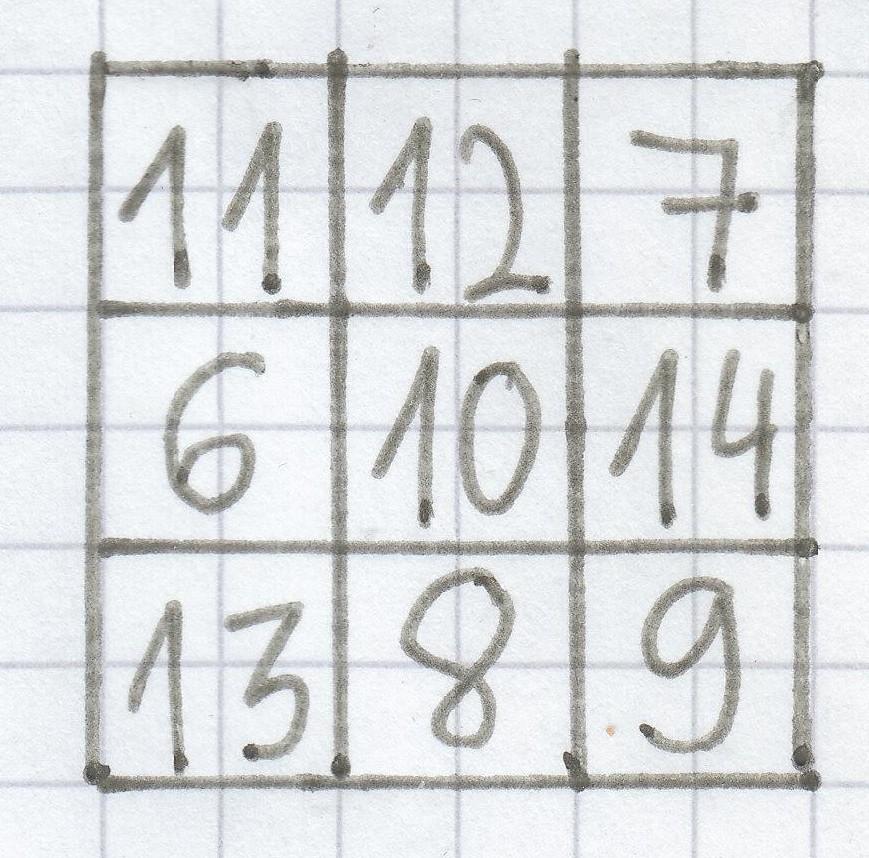
Es gibt auch Zauberquadrate mit einem 4×4-Gitter. Auch hier kommt bei jeder Zeile, jeder Spalte und jeder Diagonalen dieselbe Magische Zahl heraus, wie hier zum Beispiel die 42.
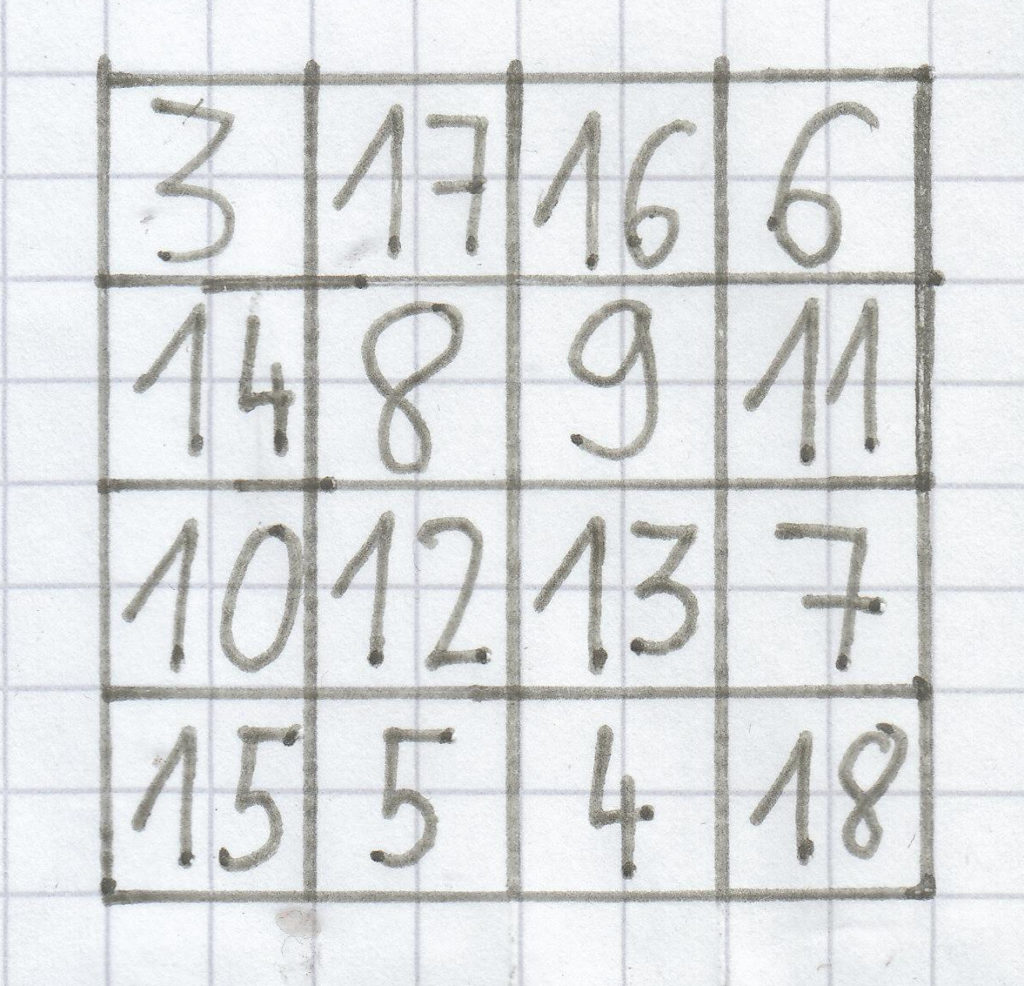
Die Zahl an Felder in der Wagrechten und Senkrechten ist übrigens bei einem Zauberquadrat nicht festgelegt, sodass es im Prinzip noch viel größere Gitter geben könnte! Schließlich handelt es sich auch bei einem XXL-Gitter wiederum um ein Quadrat, das stets wie bei kleineren Magischen Quadraten eine einzige Magische Zahl in den Zeilen, Spalten und Diagonalen vorweisen muss. Magische Quadrate machen aufgrund der Übersichtlichkeit aber nur wirklich Sinn, wenn sie eine überschaubare Anzahl an Feldern haben.
Aufgaben zu den Zauberquadraten
1. Löse das Zauberquadrat.
Diese Zahlen muss man bei dem Zauberquadrat eintragen: 8, 9, 10 und 12.
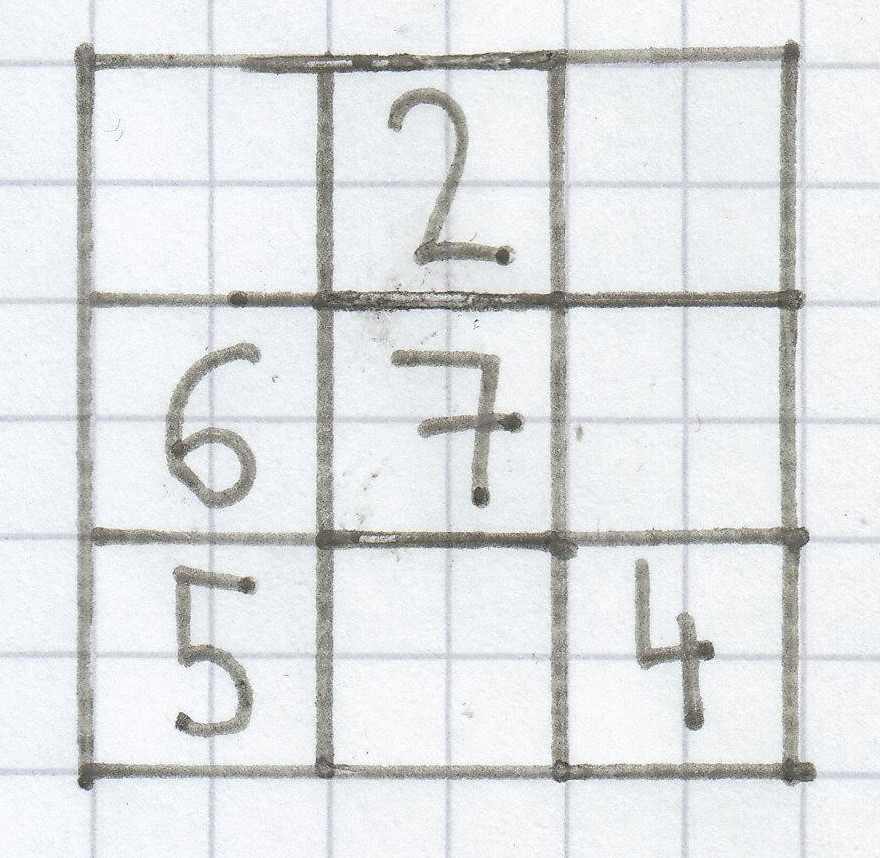
2. Bestimme die fehlenden Zahlen im Zauberquadrat
Hier muss man die Zahlen 4, 8, 9 und 12 in das Zauberquadrat eintragen.
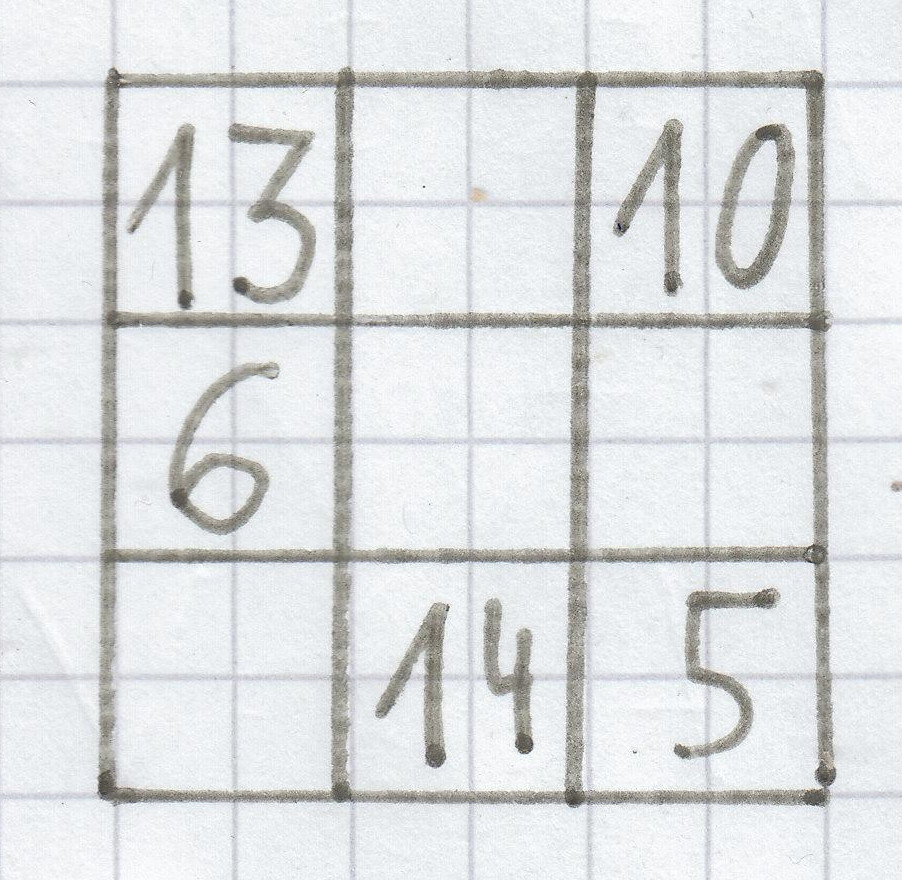
3. Vervollständige das Magische Quadrat.
Bei diesem Zauberquadrat muss man die Zahlen 6, 8, 9, 12 und 14 eintragen.
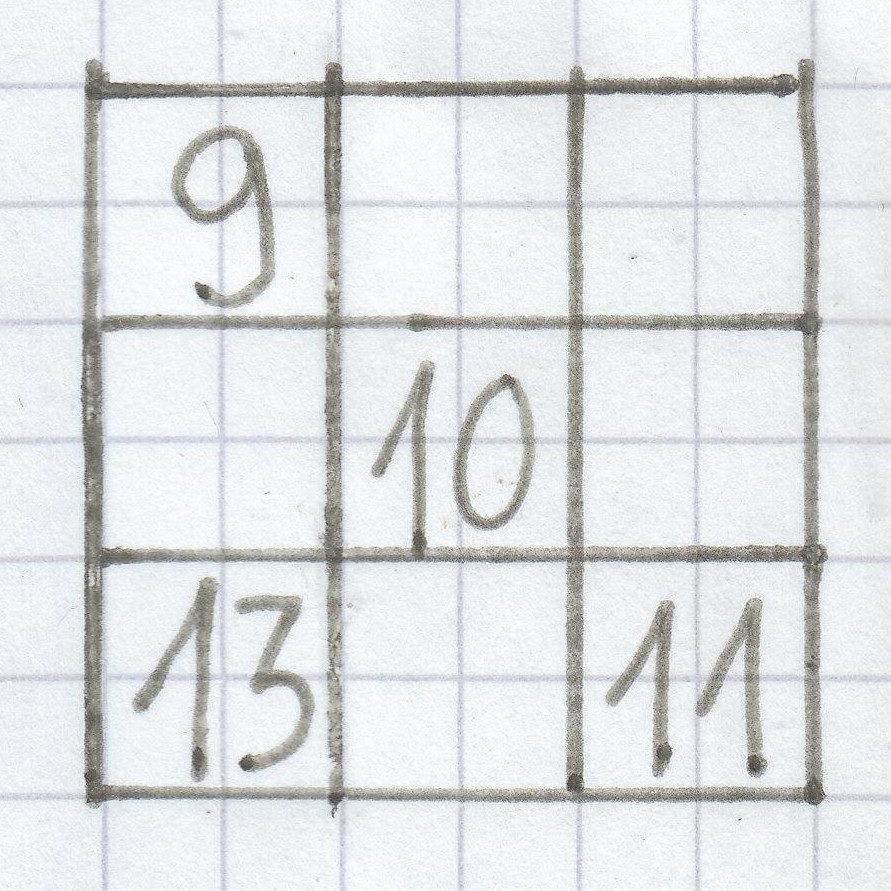
4. Bestimme beim Zauberquadrat die Zahlen der offenen Felder.
Hier muss man die Zahlen 7, 9, 12, 14, 15 und 17 eintragen.
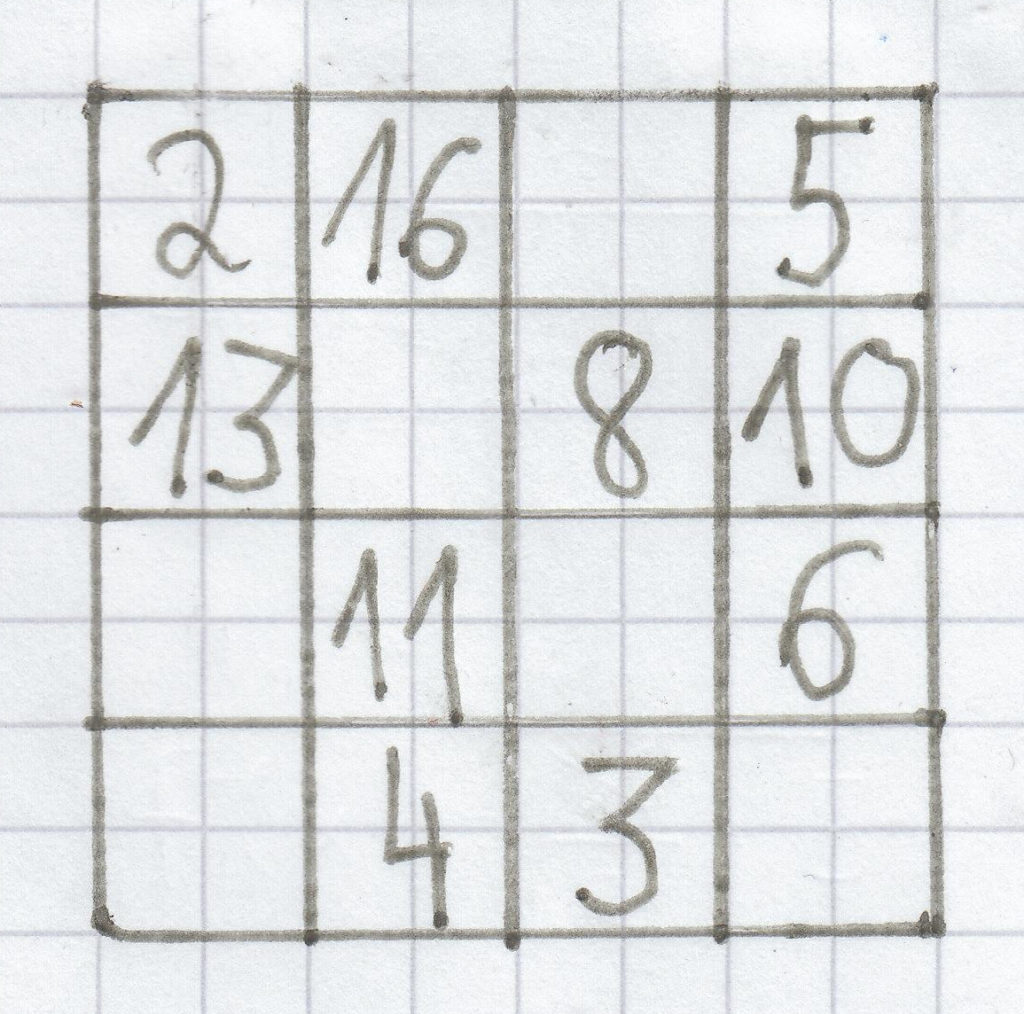
Lösungen
1. Löse das Zauberquadrat.
Diese Zahlen muss man bei dem Zauberquadrat eintragen: 8, 9, 10 und 12.
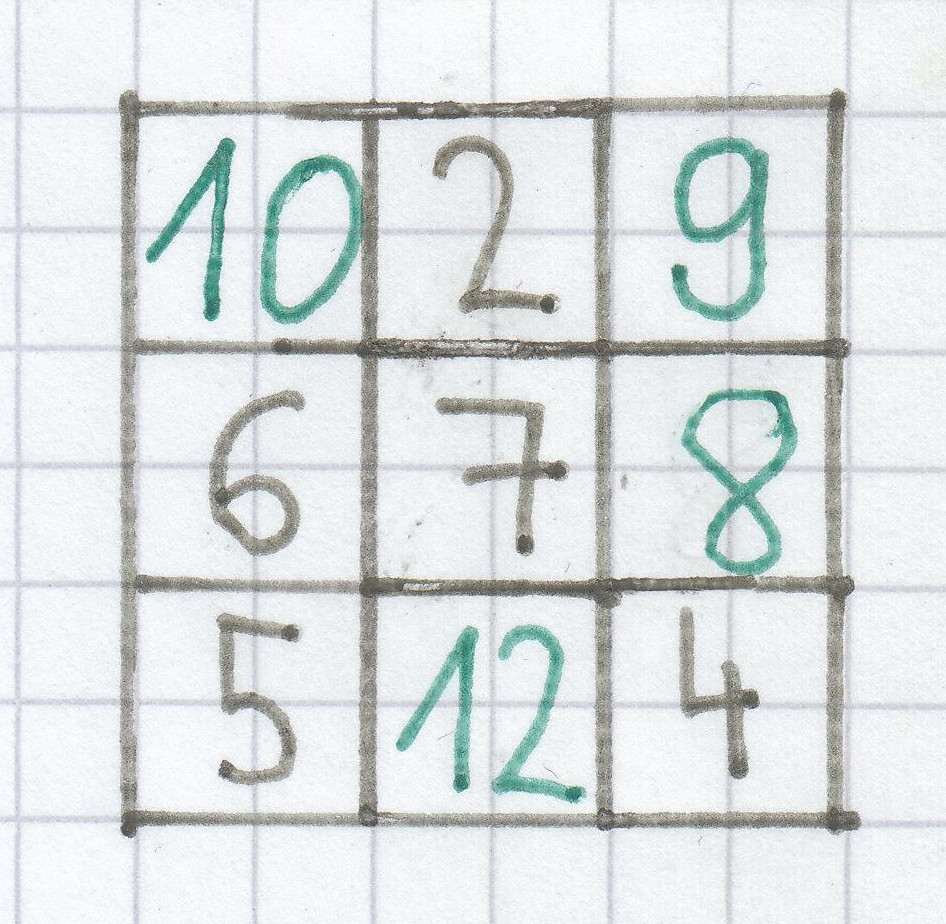
Das sollte man unbedingt als Erstes beim Lösen dieses Magischen Quadrates beachten! Man nimmt nur die Spalten, Zeilen und Diagonalen, in der stets nur eine einzige Zahl noch fehlt bzw. in der zwei Zahlen bereits gegeben sind!
In der Spalte links (von oben nach unten) stehen die Zahlen 6 und 5. Diese addiert man zusammen. Das Ergebnis ist hierbei 11. 2 und 7 stehen in der mittigen Spalte (von oben nach unten). Hier ist die Summe 9. Die Zahlen 6 und 7 sind in der mittigen Zeile, zusammen gezählt ergeben diese 13. In der Diagonale von links oben bis nach rechts unten stehen auch zwei Zahlen. Es sind die Zahlen 7 und 4. 7 + 4 ergibt wieder 11. Nur noch in der Diagonale von rechts oben bis nach links unten sind zwei Zahlen in einer Reihe. Es sind die Zahlen 7 und 5. Die Summe der beiden Zahlen ist 12.
Als Nächstes schreibt man die Summen als Gleichungen auf:
- 11 + __ = __
- 9 + __ = __
- 13 + __ = __
- 11 + __ = __
- 12 + __ = __
Am besten man orientiert sich jetzt an der kleinsten und größten Summe der addierten Zahlen. Die kleinste Summe ist 9 und die größte ist 13. Da die kleinste Zahl 9 ist, geht man nun davon aus, dass bei dieser Spalte die größte Zahl der gegeben Zahlen eingefügt werden muss, also 12. Die Magische Zahl ist dann 21. Da die 13 hier die größte Zahl ist, geht man hier nun davon aus, dass bei dieser Zeile die kleiste Zahl von den gegeben eingefügt werden muss, also die 8. Die Magische Zahl ist dann ebenso 21. Bei den anderen drei addierten Zahlen schaut man nun, dass die Gleichung ebenfalls 21 ergibt. Bei 11 ist das mit der Zahl 10 und bei 12 ist das mit der Zahl 9. Dadurch ergibt sich überall 21, was die Magische Zahl ist.
2. Bestimme die fehlenden Zahlen im Zauberquadrat
Hier muss man die Zahlen 4, 8, 9 und 12 in das Zauberquadrat eintragen.
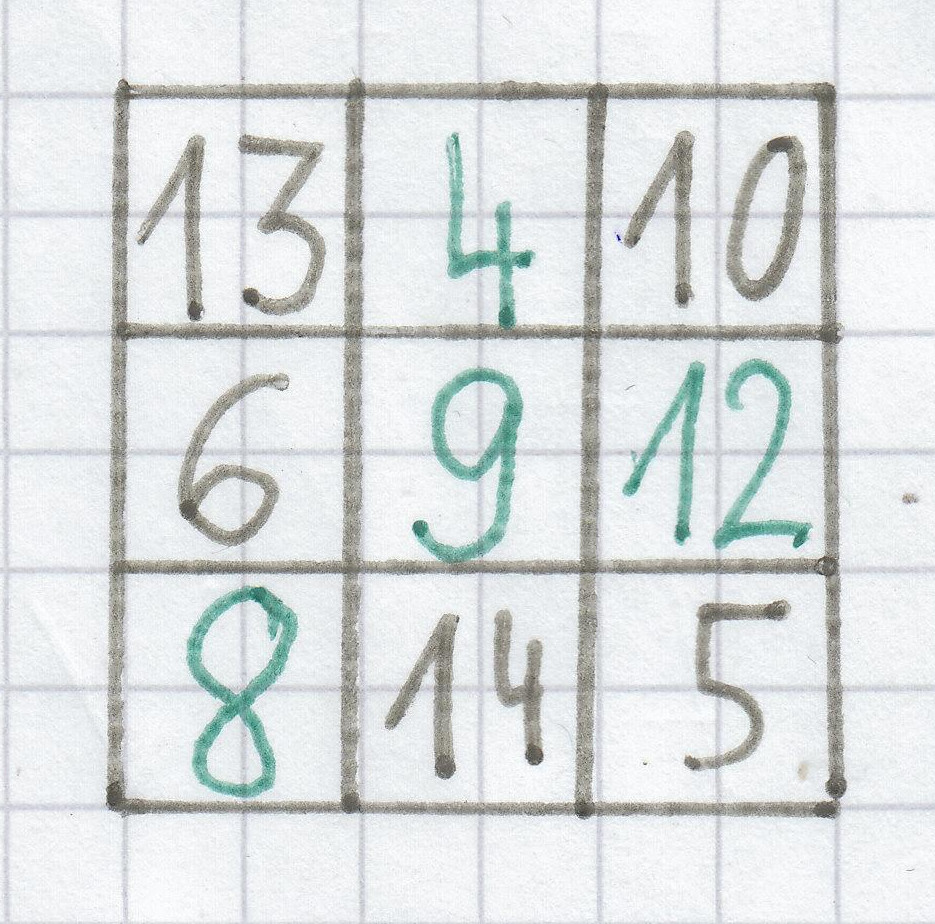
Diese Zahlen stehen in den Spalten, Zeilen und Diagonalen nur zwei mal:
In der Spalte links stehen die Zahlen 13 und 6. In der rechten Spalte stehen die Zahlen 10 und 5. Die Zahlen 13 und 10 stehen in der oberen Zeile. Die untere Zeile hat auch zwei Zahlen. Es sind die Zahlen 14 und 5. In der Diagonale von links oben bis nach rechts unten stehen die Zahlen 13 und 5.
Auch bei diesem magischem Quadrat sollte man folgene Gleichungen machen:
19 + ____ = ____
15 + ____ = ____
23 + ____ = ____
19 + ____ = ____
18 + ____ = ____
In der ersten Zeile steht zusammenaddiert bereits die Zahl 23, also eine hohe Zahl. Daher nimmt man bei der zur Auswahl stehenden Zahlen die kleinste, das ist die 4. Dadurch ergibt sich die Magische Zahl 27. ODER: Man geht von der kleinsten zusammenaddierten Zahl aus, das ist die 15. Hier nimmt man die größte Zahl von den zur Auswahl stehenden Zahlen. Das ist die 12. Dadurch ergibt sich ebenfalls die Magische Zahl 27. Mithilfe der Magischen Zahl kann man nun ohne Weiteres die noch fehlenden Zahlen in das Zauberquadrat eintragen.
3. Vervollständige das Magische Quadrat.
Bei diesem Zauberquadrat muss man die Zahlen 6, 7, 8, 12 und 14 eintragen.
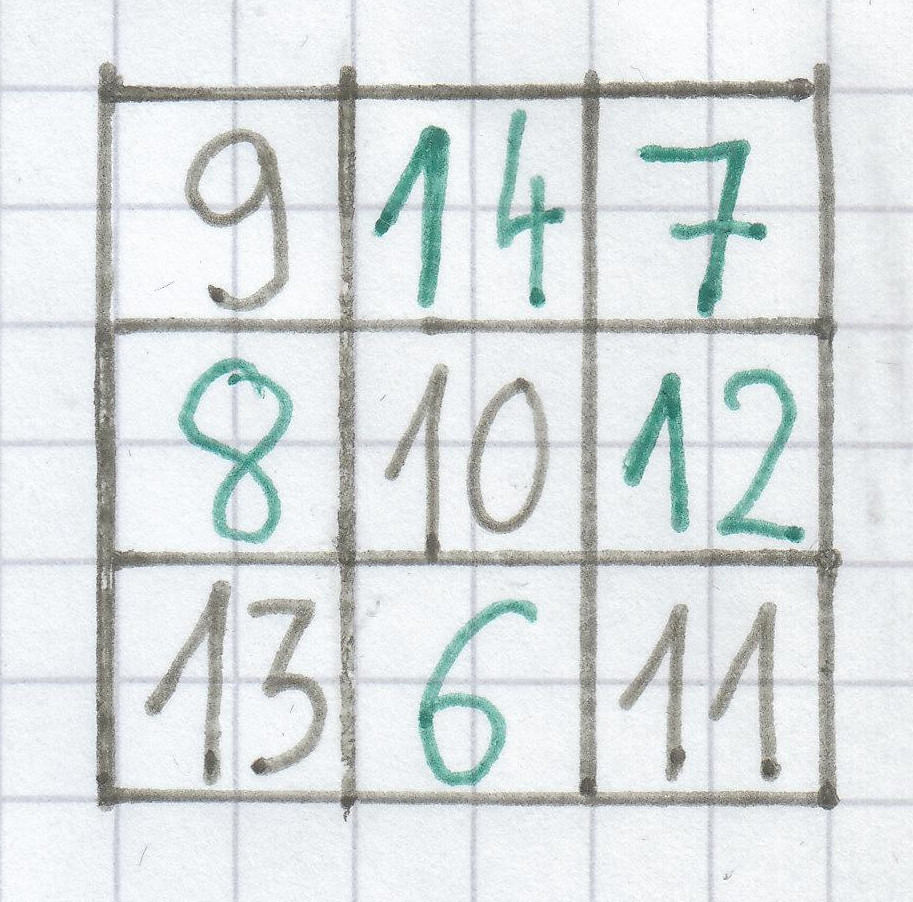
Die Magische Zahl findet man durch die Diagonale von links oben nach rechts unten raus, da in dieser Diagonale schon drei Zahlen enthalten sind! Dort sind 9, 10 und 11. Wenn man diese zusammenaddiert, ergibt sich die Magische Zahl 30.
Bei diesem Zauberquadrat hat man nun folgende Gleichungen inklusive der magischen Zahl.
22 + ____ = 30 (9 + 13 = 22)
24 + ____ = 30 (13 + 11 = 24)
23 + ____ = 30 (13 + 10 = 23)
4. Bestimme beim Zauberquadrat die Zahlen der offenen Felder.
Hier muss man die 17, die 7, die 9, die 12, die 14 und die 15 eintragen.
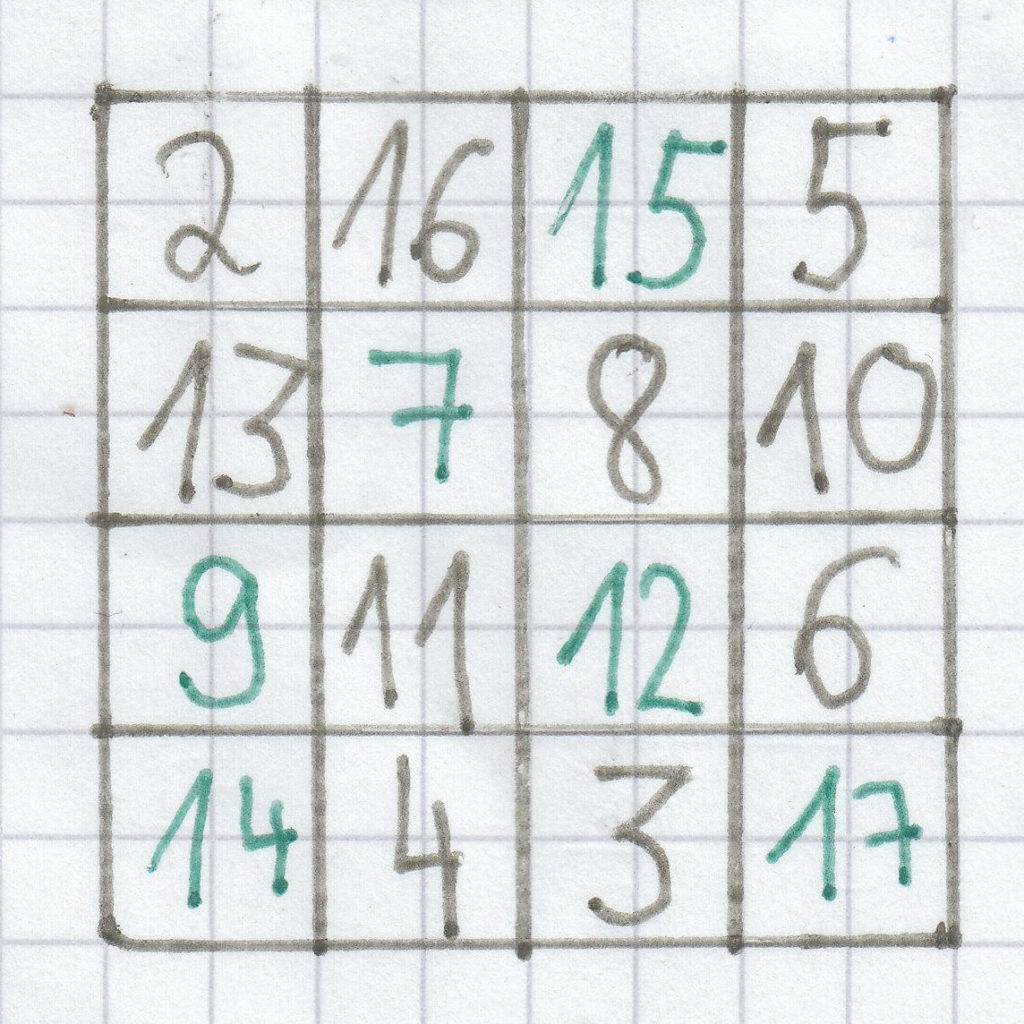
Hier macht man nur Gleichungen, wo in Diagonalen, Zeilen und Spalten drei Zahlen eingetragen sind!
In der zweiten Spalte sind die Zahlen 16, 11 und 4. Die Zahlen 5, 10 und 6 sind in der rechten Spalte. Bei der ersten Zeile sind die Zahlen 2, 16 und 5. Bei der zweiten Zeile sind bereits auch schon drei Zahlen eingetragen. Es sind die Zahlen 13, 8 und 10. In der Diagonale von recht oben nach links unten stehen die Zahlen 5, 8 und 11.
Diese Gleichungen gibt es hier:
31 + ____ = ____
21 + ____ = ____
23 + ____ = ____
31 + ____ = ____
24 + ____ = ____
Man geht nun wieder von der größten Zahl aus ODER von der kleinsten. Die größte Zahl ist die 31. Zusammenaddiert mit der zur Auswahl stehenden kleinsten Zahl 7 ergibt sich die Magische Zahl 38. Die kleinste Zahl ist die 21. Zusammenaddiert mit der größten zur Auswahl stehenden Zahl 17 ergibt sich die Magische Zahl 38. Dadurch, dass man nun die Magische Zahl hat, kann man ohne Weiteres die noch leeren Kästchen des Magischen Quadrates ermitteln.