1. Allgemeines zur Bruchrechnung
Nach dem intensiven Erlernen der Grundrechenarten, der Addition, der Subtraktion, der Multiplikation und der Division, muss irgendwann darauf in Mathe eine neue umfangreiche Rechenart gelernt werden: die Bruchrechnung. Bevor man hier aber anfängt wirklich zu rechnen, wird erst einmal erklärt, was genau ein Bruch ist und wie man einen Bruch verändern kann ohne den Wert eines Bruches zu verändern (das nennt man das Kürzen und Erweitern von Brüchen). Erst dann wird man in der Mathematik mit dem Bruchrechnen beginnen – und das wird einem unter Garantie nicht allzu schwer fallen, wenn man vorher die Grundrechenarten richtig gut gelernt hat. Bei Brüchen muss man nämlich wiederum eine Addition, eine Subtraktion, eine Multiplikation und eine Division durchführen, nur dieses Mal anstatt mit positiven ganzen Zahlen (die natürlichen Zahlen meine ich hiermit) eben mit Bruchzahlen.
2 Bestandteile einer Bruchzahl
Dadurch, dass eine Bruchzahl eine andere Zahl ist, als die bisher gelernten natürlichen Zahlen, hat diese auch logischerweise eine andere Darstellungsform. Jede Bruchzahl weist hierbei drei Charakteristika/Merkmale als Zahl auf. Sie besteht nämlich stets aus einem Zähler, das ist die obere Zahl, und einem Nenner, das ist die untere Zahl. Getrennt werden beide Zahlen durch den Bruchstrich.
Anstatt Bruchzahl ist auch gebräuchlich Bruch zu sagen, der Plural sind Brüche.

Beispiele für Bruchzahlen:
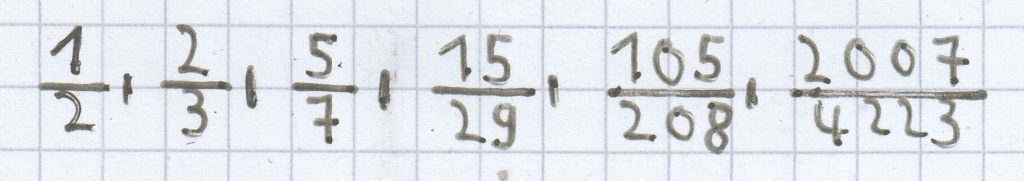
;

2.1 Ein Bruch als Ausdruck einer Division
Jeder Bruch kann im Prinzip auch als eine Division wiedergegeben werden, da der Bruchstrich nichts anderes als ein Geteiltzeichen/“:“ ist:
Beispiele für Brüche als Ausdruck einer Division:
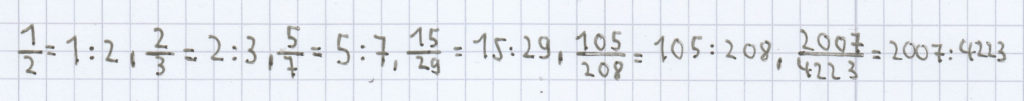
;
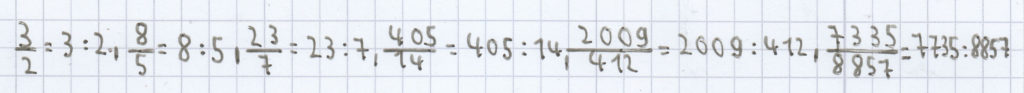
2.2 Das Verhältnis natürliche Zahl und Bruchzahl
Jede natürliche Zahl kann auch als eine Bruchzahl dargestellt werden. Daher sind alle natürlichen Zahlen eine Teilmenge der Zahlenmenge der Bruchzahlen (die Umkehrung gilt nämlich nicht!).
Beispiele:
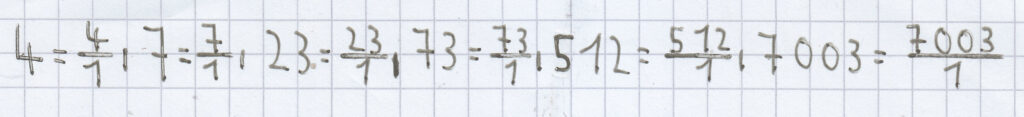
3. Bruchanteile einer bestimmten Menge
Ein Bruchzahl lernt man anfangs ist eine Teilmenge/ein Anteil von einer bestimmten Menge. Hierfür wird oft der Vergleich zu einer ganzen Pizza gezogen. Sitzen nun zwei Personen am Essens-Tisch so bekommt jede Person jeweils die Hälfte, als Bruchzahl
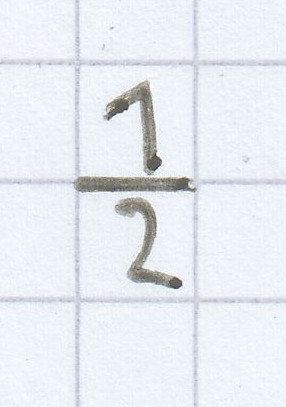
, der Pizza (vorausgesetzt man teilt die Pizza salomonisch, sprich gerecht, auf). Sitzen nun drei Personen am Tisch, so erhält jeder ein Drittel, als Bruchzahl

, der Pizza. Bei vier Personen sind es
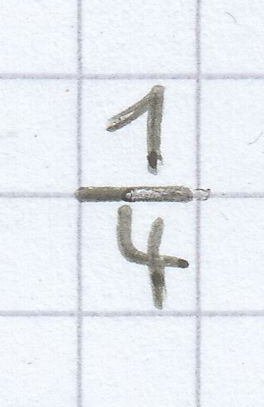
, bei fünf Personen
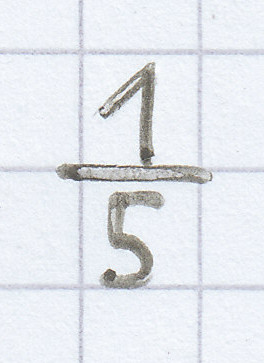
usw.
Jede natürliche Zahl kann auch als Bruchzahl dargestellt werden. So kann man beispielsweise für 1 auch
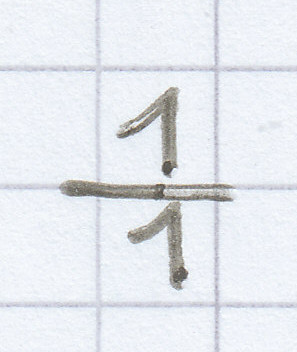
, für 2 auch

, für 12 auch

, für 523 auch

usw. schreiben. Entscheidend ist ja, dass man bei der Umwandlung von der natürlichen Zahl hin zu der Bruchzahl den Wert der Zahl nicht verändert. 1 und
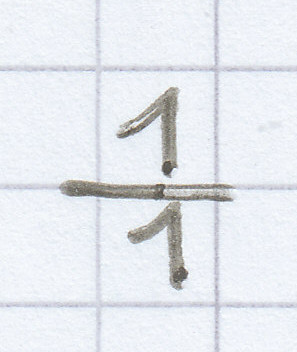
sind immer noch vom Wert her 1, 2 und

sind ebenso vom Wert her noch 2 usw.
3.1 Der Mathe-Ausdruck „von“ beim Bruchrechnen bzw. Anteile einer Gesamtmenge
Die ersten Rechenaufgaben die man in Mathe beim Bruchrechnen machen muss, sind sogenannte „von“-Aufgaben. Hierbei muss man immer einen Bruchteil/Anteil von einer Gesamtmenge berechnen.
Beispiele:

;
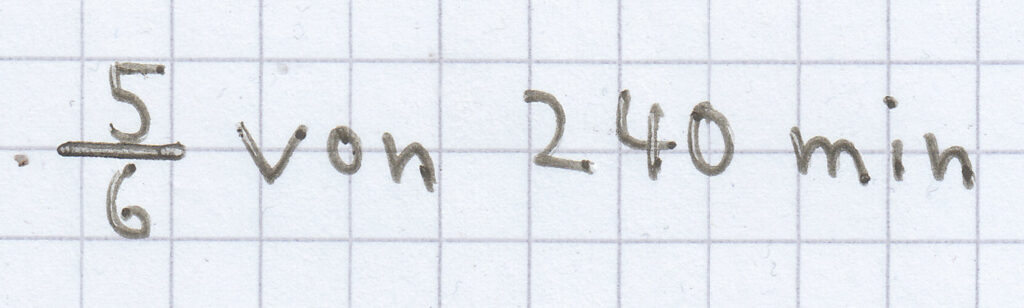
;
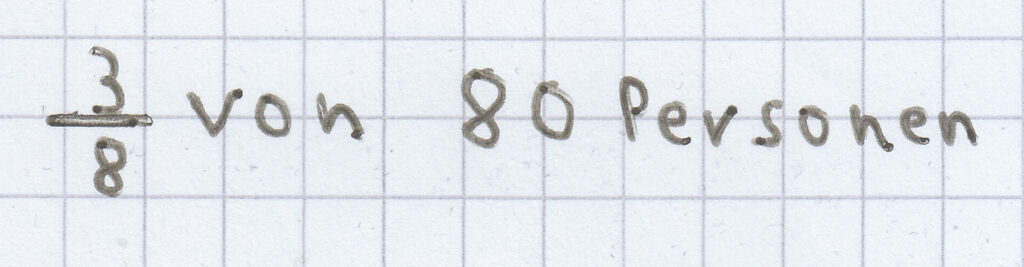
;

.
Damit man Anteile in einer verständlichen Mathe-Schreibweise wiedergeben kann, muss man vorher verstanden haben, was der Bruch oder die Bruchzahl „von“ einer bestimmten Menge in der Sprache der Mathematik bedeutet.
Beispiele:

heißt 1 m (das ist die Gesamtmenge) ∙ 4 (: 5) (das ist der Anteil) = 4 : 5 = 0,8 m = 8 dm = 80 cm. Da man aber zu diesem Zeitpunkt in der Schule in Mathe noch keine Dezimalrechnung hatte, berechnet man den „von“-Anteil normalerweise folgendermaßen: 1 m entsprechen 100 cm („mal 10, mal 10“).
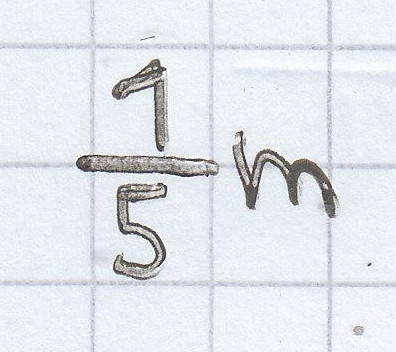
sind 20 cm („geteilt durch fünf“).

sind daher 80 cm („mal 4“).
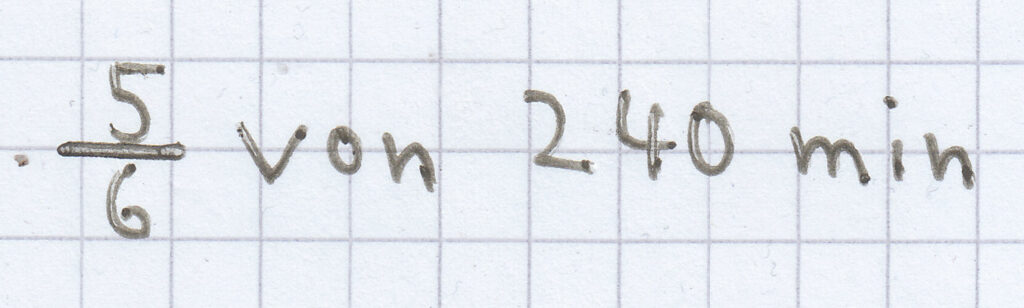
berechnet man wie folgt:

entsprechen 40 min („geteilt durch sechs“).

sind daher 200 min („mal 5“).
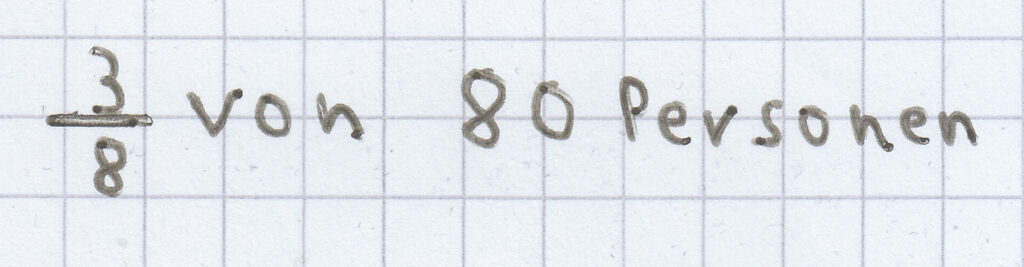
berechnet man folgendermaßen:

entsprechen 10 Personen („geteilt durch acht“).

sind daher 30 Personen („mal 3“).
[latexpage] ${\frac{8}{10}$ t von 1 t berechnet man wie folgt: 1 t entsprechen 1000 kg („mal 1000“).
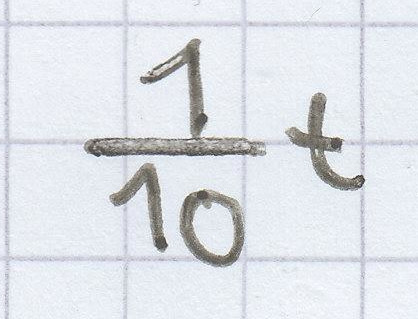
sind 100 kg („geteilt durch 10“). [latexpage] ${\frac{8}{10}$ t sind daher 800 kg („mal 8“).
Wenn man in einer höheren Klassenstufe ist oder beispielsweise den MSA (Mittleren Schulabschluss) macht, kann es sein, dass man noch einmal in Mathe mit sogenannten „von“-Aufgaben mit Brüchen konfrontiert wird. Dann sollte man aber wissen, dass in der Sprache der Mathematik ein „von“ immer mit einer Multiplikation gleichzusetzen ist. Demzufolge gibt man dann in seinen Taschenrechner nur den Anteil des Bruches mal der gegeben Gesamtmenge (was natürlich auch ein Bruch sein kann) ein.
Beispiele:
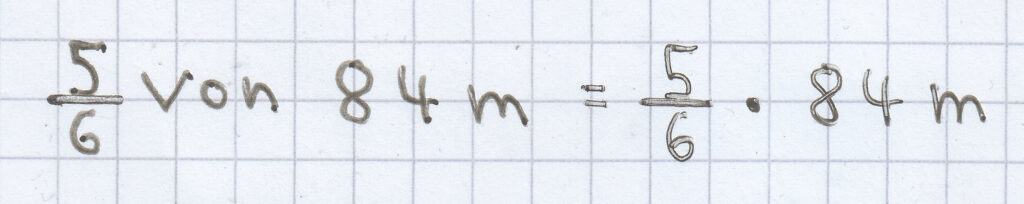
= 70 m

4. Unechte Brüche
Ein Bruch in Mathe besteht ja immer aus einem Zähler und einem Nenne, die beide durch einen Bruchstrich getrennt sind. Ist nun bei einem Bruch der Zähler kleiner als der Nenner, dann liegt ein sogenannter echter Bruch vor.
Beispiele für echte Brüche:

; [latexpage] ${\frac{3}{4}$; [latexpage] ${\frac{7}{8}$; [latexpage] ${\frac{23}{25}$; [latexpage] ${\frac{407}{455}$; [latexpage] ${\frac{1205}{7067}$
Ist nun bei einem Bruch der Zähler größer als der Nenner oder genauso groß wie der Nenner, so liegt ein sogenannter unechter Bruch vor.
Beispiele für „unechte Brüche“:
[latexpage] ${\frac{4}{3}$; [latexpage] ${\frac{7}{4}$; [latexpage] ${\frac{12}{5}$; [latexpage] ${\frac{35}{19}$; [latexpage] ${\frac{41}{41}$; [latexpage] ${\frac{407}{122}$; ${\frac{555}{555}$; ${\frac{3107}{241}$;
4.1 Das Umrechnen eines unechten Bruchs in einen gemischten Bruch
Jeden unechten Bruch kann man, vorausgesetzt der Zähler ist nicht genauso groß wie der Nenner, in einen sogenannten gemischten Bruch umrechnen. Ein gemischter Bruch besteht hierbei aus einer ganzen Zahl und einer Bruchzahl, wobei die ganze Zahl immer direkt vor die Bruchzahl gestellt wird.
Beispiele für gemischte Brüche:
[latexpage] 2${\frac{1}{2}$; [latexpage] 4${\frac{3}{4}$; [latexpage] 8${\frac{7}{9}$; [latexpage] 12${\frac{24}{55}$; [latexpage] 5${\frac{79}{83}$; [latexpage] 27${\frac{403}{607}$; 503${\frac{8603}{9979}$;
Einen unechten Bruch rechnet man nun immer wie folgt in einen gemischten Bruch um:
Dieser unechte Bruch ist gegeben: [latexpage] ${\frac{17}{3}$. Mittels einer Division wandelt man nun den Buch um. Hierfür ist es sinnvoll den Bruch in der gewohnten Divisionsschreibweise darzustellen:
Bei jedem Bruch kann ein Bruchstrich auch in eine Divisionszeichen umgewandelt werden, der Zähler wird dann zum Dividend und der Nenner zum Divisor.
[latexpage] ${\frac{17}{3}$ = 17 : 3
Darauf führt man die Division durch, wie man diese vorher in Mathe gelernt hat.
17 : 3 = 5
[latexpage] ${\underline{15}$
2 Rest
Die drei „passt“ in die 17 5-mal, das ergibt die ganze Zahl des gemischten Bruchs. Die Bruchzahl aus dem gemischten Bruch enthält als Zähler die 2, dem Rest der Division, und als Nenner die 3, den Nenner des unechten Bruchs.
Daher ist der gemischte Bruch zu dem unechten Bruch [latexpage] ${\frac{17}{3}$ = [latexpage] 5${\frac{2}{3}$
Bei der Umwandlung vom unechten Bruch zum gemischten Bruch erhält man die ganze Zahl des gemischten Bruchs immer durch die Durchführung einer Division. Der Divisions-Rest ist beim gemischten Bruch immer der Zähler der Bruchzahl . Der ursprüngliche Nenner beim unechten Bruch ist immer gleich dem Nenner bei der Bruchzahl, die bei einem gemischter Bruch enthalten ist.
Beispiele für die Umwandlung unechter Brüche in gemischte Brüche:
[latexpage] ${\frac{29}{4}$ = 29 : 4
29 : 4 = 7
[latexpage] ${\underline{28}$
1 Rest
Daher ist der gemischte Bruch:[latexpage] 7${\frac{1}{4}$
[latexpage] ${\frac{88}{5}$ = 88 : 5
88 : 5 = 17
[latexpage] ${\underline{85}$
3 Rest
Deshalb ist hier der gemischte Bruch:[latexpage] 17${\frac{3}{5}$
[latexpage] ${\frac{215}{12}$ = 215 : 12
215 : 12 = 17
[latexpage] ${\underline{12}$
95
[latexpage] ${\underline{84}$
11 Rest
Daher ist hier der gemischte Bruch:[latexpage] 17${\frac{11}{12}$
4.2 Das Umrechnen eines gemischten Bruchs in einen unechten Bruch
Des Öfteren muss man beim Bruchrechnen auch einen gemischten Bruch in einen unechten Bruch umwandeln. Hierzu multipliziert man die ganze Zahl mit dem Nenner des Bruchs. Das Ergebnis addiert man schließlich mit dem Zähler des Bruchs. Die sich hierbei ergebende Zahl ist der neue Zähler des unechten Bruchs, der Nenner des gemischten Bruchs bleibt auch beim unechten Bruch erhalten.
Das Umrechnen vom gemischten Bruch hin zum unechten Bruch ist im Bruchrechnen einfach die umgekehrte Rechenoperation zum Umrechnen eines unrechten Bruches in einen gemischten Bruch.
Beispiele für die Umwandlung gemischter Brüche in unechte Brüche:
[latexpage] 4${\frac{1}{2}$, der Zähler des unechten Bruchs = 4 · 2 + 1 = 9, der Nenner des gemischten Bruchs bleibt erhalten: [latexpage] ${\frac{9}{2}$
[latexpage] 6${\frac{2}{5}$, der Zähler des unechten Bruchs = 6 · 5 + 2 = 32, der Nenner = 5: [latexpage] ${\frac{32}{5}$
[latexpage] 32${\frac{4}{7}$, der Zähler des unechten Bruchs = 32 · 7 + 4 = 228, der Nenner = 7: [latexpage] ${\frac{228}{7}$
5. Dezimalbrüche
Brüche, die im Nenner die Zahl 10 oder eine Potenz von 10 mit natürlichem Exponenten vorweisen, nennt man Dezimalbrüche.
Beispiele von Dezimalbrüchen:
[latexpage] ${\frac{7}{10}$; ${\frac{29}{100}$; ${\frac{335}{1000}$; ${\frac{12}{100000}$